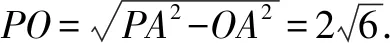正四棱锥创设,创新情境应用
——基于一道教材习题的探究
2023-02-11陈瑞霞
陈瑞霞
中国核工业集团公司二○二厂中学
立体几何中的边、角、面积或体积等要素的取值范围或最值问题,一直是高考中立体几何部分知识考查的一个热点与创新点,融入立体几何中的“动”与“静”的对立与统一,“数”与“形”的综合与转化,数学知识、数学能力与核心素养等方面的考查得以全面兼顾,倍受关注.此类问题经常通过对高中数学教材中的例(习)题进行重新加工,借助问题背景包装,空间几何体建立,条件或结论的变换等多种方式,创新应用,看似平常,实则蕴含很多值得好好品味的东西.
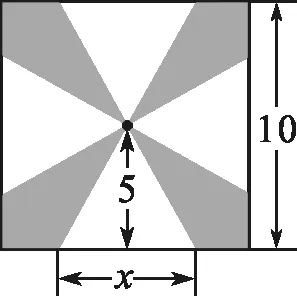
图1
1 源于教材
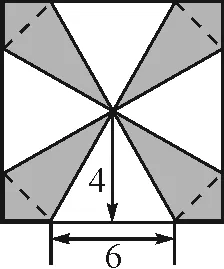
习题(人民教育出版社2019年国家教材委员会专家委员会审核通过的《数学(必修第二册A版)》第八章“立体几何初步”中复习参考题8第169页第4题)如图1,一块边长为10 cm的正方形铁皮上有四块阴影.将这些阴影部分裁下来,然后用余下的四个全等的等腰三角形加工成一个正四棱锥形容器,把容器的容积V(单位:cm3)表示为x(单位:cm)的函数.
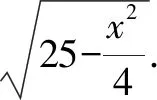
俗话说得好:铁打的营盘流水的兵.高考中考查不变的是数学知识、数学思想方法与数学技巧等,变化的是问题情境的呈现方式以及问题的结构形式,以及设问的视角等.这就要求我们立足并深耕高中数学教材中的知识与例(习)题,学会突破常规,陈题巧改编,“旧瓶”装“新酒”.
2 链接高考
在强调高考命题改革与创新的背景下,通过对高中数学教材中的例(习)题进行改编、组合、深入、创新等手段来赋予课本例(习)题新的面貌、新的生命,已经成为高考数学命题的一种新趋势、新风尚.
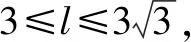

分析:该高考真题以课本例(习)题中的正四棱锥为背景,以及把该正四棱锥的体积表示为某个变量的函数,合理添加四棱锥的外接球这个创新场景,在原课本例(习)题的基础上,增加难度与广度,综合考查空间几何体之间的位置关系、体积以及导数法或均值不等式等,实现问题的变式、拓展与创新.
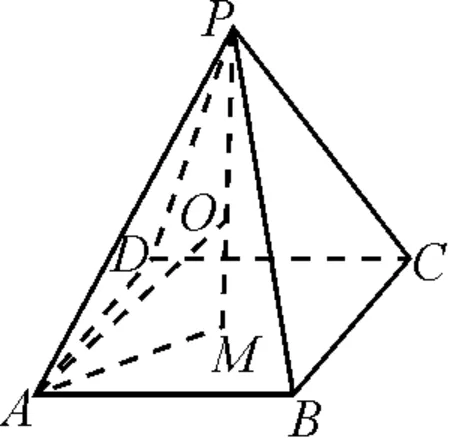
图2
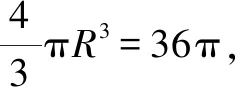
设PM=h,AM=a,则(h-3)2+a2=9,且l2=h2+a2∈[9,27].
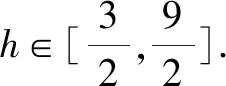
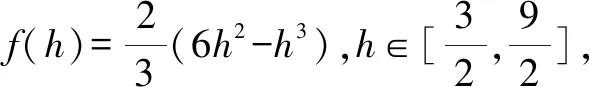
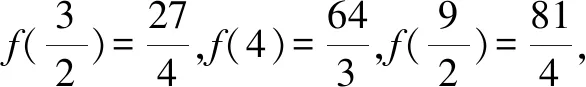
故选择答案:C.
点评:具体设参时,可以以正四棱锥的高为变量,以正四棱锥的侧棱长为变量,或以正四棱锥的侧长与高所对应的角为变量,都可以合理构建对应的函数关系式,进而利用导数法或均值不等式法来确定对应的最值问题,实现问题的突破与解决.

答案:C.
3 场景创新
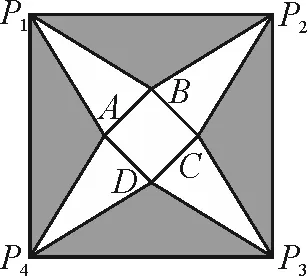
图3
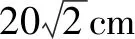
分析:以不同的方式显现正四棱锥,通过底面正方形边长的设置,结合正四棱锥的高的求解来确定其参数的取值范围,进而确定边长AB的取值范围;结合正四棱锥的体积的表达式的构建,利用函数的设置与导数来确定其最值,进而得以确定此时边长AB的值.

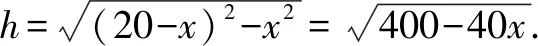
由400-40x>0,解得x<10,所以边长AB的取值范围为(0,20).

设函数f(x)=100x4-10x5(0 所以当0 所以当x=8时,f(x)取得极大值也为最大值,此时AB=16 (cm). 故填答案:(0,20);16. 点评:通过不同形式的正四棱锥的构建来创设问题场景,结合正四棱锥的体积与对应变量的关系,利用导数法或均值不等式法等来确定对应的最值,以不同的方式、相同的考点巧妙设置. 图4 例3[2023届河北省唐山市高三(上)摸底数学试卷]如图4,一块边长为8的正方形铁片上有四块全等的阴影部分.将空白部分剪掉,对余下阴影部分按下面工序加工成一个正四棱锥:将四块阴影部分分别沿虚线折叠,以其中等腰直角三角形组成棱锥的底面,余下为棱锥的侧面.则所得正四棱锥的外接球表面积是( ). 分析:以不同的方式显现正四棱锥,利用正四棱锥的确定以及与之对应的外接球的联系,进而求解对应正四棱锥的外接球的表面积,从另一个视角来探究与应用. 图5 解析:依题意可得如图5所示的正四棱锥P-ABCD.设点O为正方形ABCD的中心. 连接PO,则PO⊥平面ABCD. 因为OA⊂平面ABCD,所以PO⊥OA. 故选择答案:C. 点评:通过不同形式的正四棱锥的构建来创设问题场景,结合正四棱锥与其外接球的结构特征来构建两者之间的关系,为相关参数的确定与求解提供条件,从问题场景的设置与空间几何体的联系等视角来创新与应用. 近几年新高考数学中立体几何试题的命制,呈现越来越灵活多变,形式越来越新颖多样,但万变不离其宗,大多数高考试题都可以在教材中追根溯源,寻觅其影踪,找到其原型.因而,在高考复习备考过程中,全面回归教材,注意对课本中典型例(习)题的练习与变式训练,理解其内涵,规范其步骤,把握其实质,掌握其规律,真正做到胸有成竹,“胸中有本”.Z