高考理科数学试题综合难度的演进趋势

曹翛骛 郭三刚

陕西理工大学

1 引言

高考数学试题具有选拔人才的功能，但由于考试时长的限制，所以试题内容既要全面，又要有重点和难点，这就需要命题人合理把控试题难度.试题难度通常用全体考生的考试及格率来度量，这种度量方法着眼于考试结果，没有考虑影响试题难度的客观因素，不便于考试前试题难度的把控，因此有必要构建一种客观的试题难度系数衡量标准和检测办法.

鲍建生[1]提出了数学课程综合难度模型，其认为影响数学课程综合难度的主要因素有探究、背景、运算、推理和知识含量5个方面，且不同因素又划分为不同的等级水平，并给予等级变量的自然赋值，然后加权平均得到习题的综合难度系数，并将此方法用于比较中英两国初中数学课程综合难度.武小鹏等[2]在鲍建生的综合难度模型中增添了参数和思维方向两个因素，以此研究了中韩两国高考数学试题的难度，结果是：我国高考数学试题综合难度偏高.而影响数学试题难度的因素很多，各因素的影响力也不同，在各影响因素作用大小准确给定的前提下，能部分提高定量化测量试题难度的准确性.20世纪70年代匹兹堡大学的Saaty教授(Thomas L.Saaty，Saaty，1926-2017)提出了层次分析法(Analytic Hierarchy Process，AHP)[3].

层次分析法是一种较好的权重确定方法，可以把复杂问题中的各因素划分成相关联的有序层次，进而决策[4].

武小鹏等[5]采用层次分析法对自己改进后的综合难度系数模型中的不同因素及其不同水平赋权，进一步提高了综合难度模型的可用性.

本文中将武小鹏等改进后的综合难度系数模型做了一些调整，利用层次分析法得到了各影响因素及其不同水平的权重系数，并以2013—2020年全国Ⅱ卷、2021—2022年全国乙卷的高考理科数学试卷为研究样本，分析了上述连续10年试题综合难度的演进趋势.

2 综合难度系数模型建立与求解

武小鹏等[5]改进后的综合难度系数模型中因素有背景、参数、运算、推理、知识含量、思维方向和认知等7个.本文中没有将参数作为一个因素处理，因为运算是利用已知量(数值或符号的表达式)经过一系列数学操作获得新的量的过程，参数或者是问题本身的若干变量，或者为求解问题而引入的若干变量，因而参数属于运算的成分，可以不作为影响试题难度的因素单独考虑.为了能够突出因素不同水平的差异性，增加或减少了因素的水平数，调整了同一因素不同水平的赋值.具体地，本文建立的综合难度系数模型采用了情境、运算、推理、知识含量、思维方向和认知等六个难度因素，并调整了运算和认知两个因素各自的难度水平，在情境、推理、知识含量、思维方向等四个因素的难度水平采用武小鹏等[5]的划分，并赋值了各影响因素的不同水平，见表1.

皇甫倩等[6]认为数学技能是影响定量化试题难度的一个因素，根据问题对技能的要求和运算的复杂性将数学技能中的简单符号运算与复杂数值运算归为一个水平.本文中据此将运算划分为简单运算、较复杂运算和复杂运算等三个水平，其中，简单运算指简单数值运算，较复杂运算包括复杂数值运算(如，指对数等数值运算)和简单符号运算(如，3步以内的含字母运算)，复杂运算指复杂符号运算(如，复杂的含字母运算和复杂的推理证明).

顾泠沅[7]提出的数学认知因素分析框架为：水平1，计算——操作性记忆水平(如，简单的计算，作图和求值)；水平2，概念——概念性记忆水平(如，数学定义和性质等的记忆)；水平3，领会——说明性理解水平(指能够灵活使用数学方法，理解题干信息并掌握推理思路)；水平4，分析——探究性理解水平(指综合运用知识，并能从多视角分析问题，创造性地解决非常规问题).本文中借鉴该数学认知水平框架，将认知划分为记忆、领会和探究等三个水平，因为水平1和水平2同属记忆水平.其中，记忆指“计算——操作性记忆水平”和“概念——概念性记忆水平”，领会指“领会——说明性理解水平”，探究指“分析——探究性理解水平”.

一套试题综合难度系数的计算如下：

(1)先计算各因素的难度系数di，采用鲍建生[1]在综合难度模型中计算各因素的难度系数的公式：

其中，di(i=1,2,……,6)分别对应背景、运算、推理、知识含量、思维方向和认知等六维影响因素的难度系数，wij指第i个因素的第j个水平的权重系数，nij是所有题目中第i个因素所处第j个水平的题目个数，k指各个因素的水平个数，n为试题题目的总数.

(2)再计算一套试题的综合难度系数D，综合难度系数是各因素难度系数的加权平均值，即

其中，wi指第i个影响因素的权重系数.

因素的难度系数di和试题综合难度系数D数值越大，意味着相应难度越大.

为计算试卷的综合难度，本文中利用层次分析法获取因素及其水平的权重系数.根据3位学科教学(数学)的硕士生导师和7位高中数学教师对表1综合难度系数模型中因素和水平同层次间要素的相对重要性作出的评判结果，构造出因素和水平间的判断矩阵，并求解它们的最大特征根及相应的特征向量，经一致性检验，发现上述判断矩阵均具有一致性[4].

由此得出了各因素的权重系数wi和各因素水平的权重系数wij：w1=0.04，w2=0.08，w3=0.08，w4=0.12，w5=0.34，w6=0.34；w11=0.11，w12=0.26，w13=0.63，w21=0.09，w22=0.22，w23=0.69，w31=0.14，w32=0.86，w41=0.10，w42=0.21，w43=0.69，w51=0.20，w52=0.80，w61=0.10，w62=0.21，w63=0.69.

如下示例说明如何统计1道试题在各因素上的水平分布.

例(2022年全国乙卷理科第14题)过四点(0，0)，(4，0)，(-1，1)，(4，2)中的三点的一个圆的方程为____________.

分析：该题考查圆的一般方程和性质，是一道无背景试题，只需设出圆的一般方程，任选三个点代入，得到方程组解之即可，主要考查学生的数学运算素养.故该题在各因素分别处于无背景、简单符号运算、简单推理 、2个知识点、顺向思维和记忆水平.

3 近10年高考理科数学试题的综合难度

3.1 影响因素的分布情况

通过统计，绘制出2013-2020年高考理科数学全国Ⅱ卷和2021-2022年高考理科数学全国乙卷分别在六个影响因素上的水平分布，见图1～6.

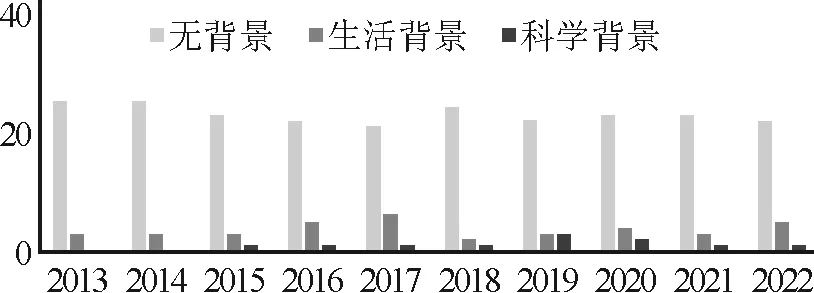
图1 情境分布

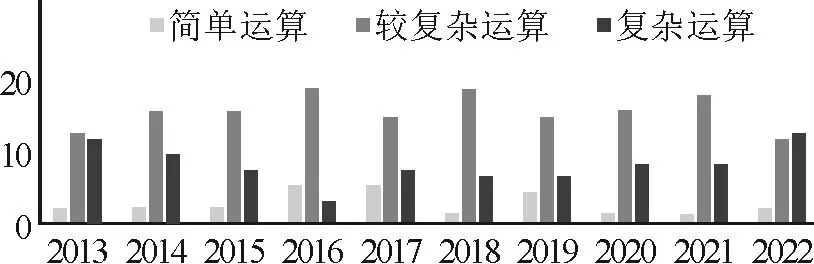
图2 运算分布

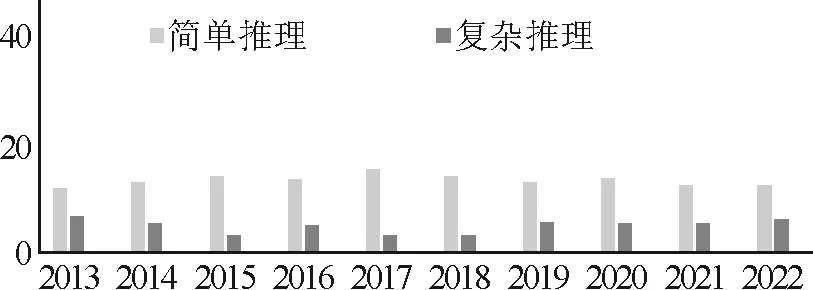
图3 推理分布

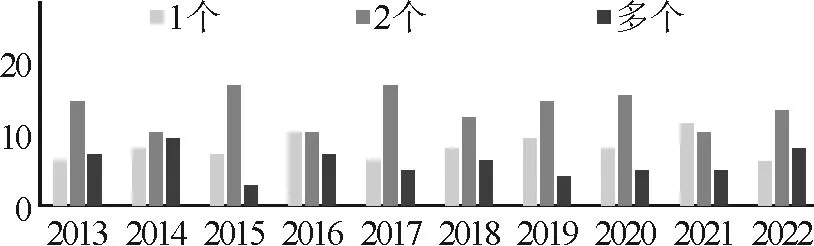
图4 知识含量分布

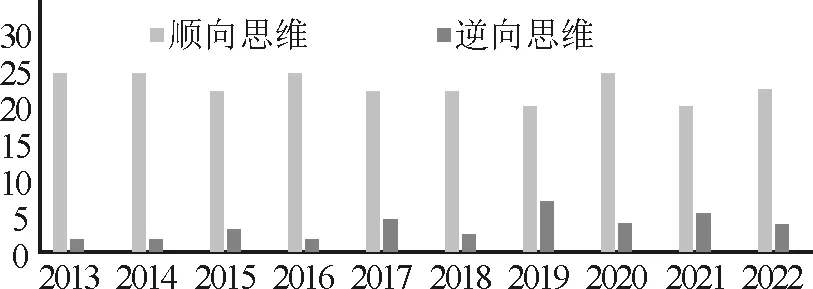
图5 思维方向分布

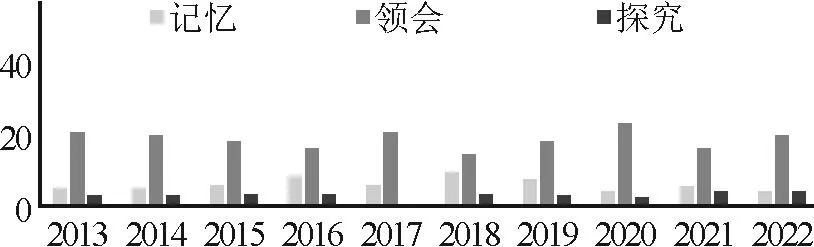
图6 认知分布

图1～6可以直观反映出六维因素的各水平分布情况.就背景而言，分布在无背景的题目始终居多，但从2015年起，生活背景和科学背景的题目逐渐增多；运算分布上，较复杂运算最多，复杂运算次之，简单运算最少；就推理而言，多以考查简单推理为主，分布基本稳定；知识含量上，2个知识点的考查最多，1个知识点和多个知识点的考查分布相当；思维方向上，绝大部分题是以顺向思维解题的，逆向思维的运用很少；对于认知，领会水平的题目最多，记忆和探究水平的题目分布较少.

3.2 影响因素难度系数的变化趋势

根据统计和计算结果，绘制10年样本试题在六维因素难度系数上的变化折线图，如图7.

图7 各因素难度系数变化趋势

从图7看来，各套试题中运算和推理的难度系数最大，即侧重于考查运算求解能力和逻辑思维能力；情境的难度系数远远小于其他，但总的趋势是处于上升的；思维方向的难度系数大致在增长；知识含量的难度系数在0.24～0.31不断波动变化；认知的难度系数的极差为0.3，变化最为稳定.

3.3 综合难度系数的演进趋势

经计算得出各套卷的综合难度系数，并绘制10套试卷综合难度系数的变化趋势折线图，见图8.

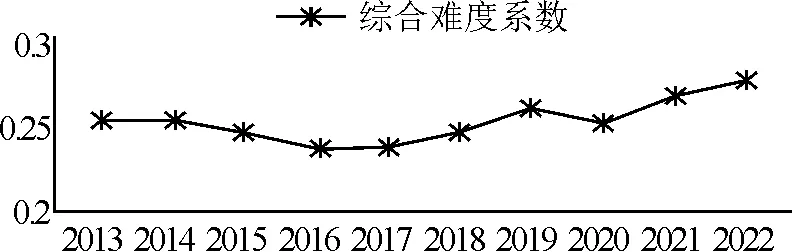
图8 综合难度系数演进趋势

由图8可知，2013-2020年高考理科数学全国Ⅱ卷和2021-2022高考理科数学全国乙卷的综合难度先降后升.其中，2013-2014年试卷的综合难度基本持平，2014-2017在逐渐下降， 2017-2022年期间的试卷综合难度整体呈现出上升趋势，2017年高考理科数学全国Ⅱ卷的综合难度最小， 2022年高考理科数学全国乙卷的综合难度最大.

4 结论

本文中通过建立综合难度系数模型，并用层次分析法求解，研究了连续10年试卷(2013-2020年高考理科数学全国Ⅱ卷和2021-2022高考理科数学全国乙卷)综合难度的演进趋势，下面是结论与建议.

高考理科数学全国Ⅱ卷于2021年变更为全国乙卷，变更后，全国乙卷的综合难度均在历年全国Ⅱ卷之上，特别是今年(2022年)的综合难度是10年间最大的.但变化前后均侧重于考查学生的数学运算和逻辑推理素养，所以在日常教育教学中，需要格外注重这两个素养的培养.就情境而言，历年始终以无背景题目居多，近年来情境题目逐渐增加，有利于培养和提高学生对生活、社会和科学的信息识别与加工能力，以及数学建模素养和数学抽象素养；在运算上，以考查较复杂运算为主，对考生的运算能力有一定的要求，要加强学生运算求解能力的培养；对于推理，推理步骤反映了学生解题思维的复杂程度，而历年考查简单推理的题目居多，表现出高考数学试题注重基础性，但不能忽略对逻辑推理素养的培养；就思维方向而言，虽然以顺向思维解题为主，但逆向思维有利于发展学生的创新能力，因此同样不可忽视；从知识含量和认知角度看，主要考查2个知识点的综合运用，1个和多个知识点的考查也有一定分布，处于领会水平的题目最多，记忆和探究水平的题目较少，但都有一定的设置.由此得出，高考数学在面向大部分考生群体的同时，又具有选拔人才的作用 ，充分体现了高考数学试题“低起点、多层次、高落差”的难度调控，整体兼顾了基础性、应用性、综合性和创新性[8].