基于韦伯模式的高考数学试卷与课程标准一致性研究——以2022年、2021年新高考数学Ⅰ卷为例

徐明月

哈尔滨师范大学教师教育学院

1 问题的提出

新修订的课程标准在高考命题原则中提到:“命题应依据学业质量标准和课程内容，充分考虑对教学的积极引导作用，同时发挥数学高考的选拔功能．”为此，笔者从知识种类、知识深度、知识广度以及知识分布平衡性四个方面对2021，2022年新高考数学Ⅰ卷与课程标准的一致性进行研究，以期能够对高考命题及复习备考有所帮助．

2 研究设计与实施

2.1 研究的设计

本研究选用美国学者诺曼•韦伯研发的韦伯一致性分析模式.诺曼•韦伯将课程的内容结构按照类似三角形的稳定结构——金字塔层级来划分，其中内容维度从知识种类、知识深度、知识广度以及知识分布平衡性四个方面进行研究．

2.2 研究的实施

笔者选取2022年和2021年新高考数学Ⅰ卷进行研究，将试卷中每一道题目涉及的知识点按照课程标准中的四大主线进行分类，并统计出课标中四大主线课程内容的具体目标数，同时将课程目标中提到的行为动词归为“了解”“理解”“掌握”三个层次，并对每一个层次的水平进行界定．

3 数据分析

3.1 知识种类一致性分析

知识种类一致性研究的是学业评价与课程标准是否陈述了相同的内容范畴，可以根据评价试题是否包含了每一条标准的相应内容，来判断知识种类一致性是否达成．韦伯认为评价必须至少6次“命中”某一条标准的内容，其知识种类一致性才可以接受．

2022年和2021年新高考数学Ⅰ卷知识种类一致性分析如表1所示．

表1 新高考数学Ⅰ卷知识种类一致性分析

从表1中可以发现，两年的试卷中预备知识主线击中目标的题目均少于6道，均未达到一致性可接受水平，而函数、几何与代数和概率与统计三个主线两年击中目标的题目均大于6道，均达到了一致性可接受水平．整体来看，2022年和2021年新高考数学Ⅰ卷的知识种类一致性均较好．

3.2 知识深度一致性分析

知识深度一致性是要检验评价所要求学生展示的认知水平与课程标准中所期望的学生所应知道与做到的认知表述是否保持一致．韦伯认为测验试题的认知水平至少有50%“命中”课程标准的某个目标所要求的认知水平才达到了一致性可接受水平．

近两年新高考数学Ⅰ卷知识深度一致性分析如表2．

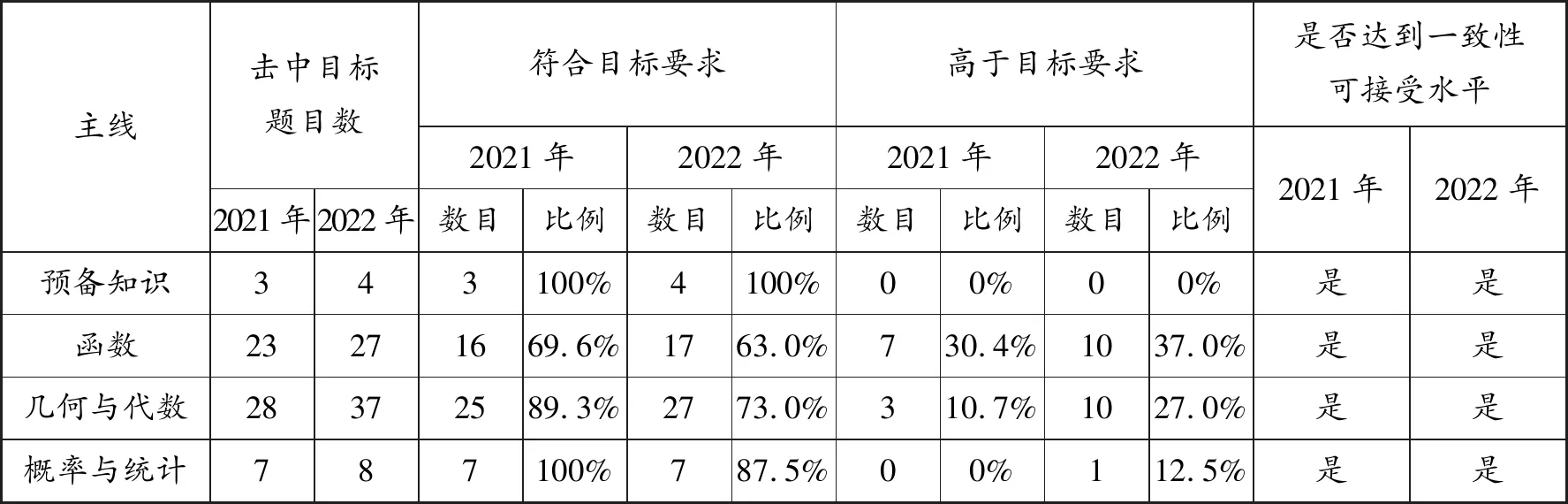
表2 新高考数学Ⅰ卷知识深度一致性分析

从表2中可以发现，2022年和2021年新高考数学Ⅰ卷中四个主线符合目标要求的题目数占比均高于50%，即两年试卷的知识深度均达到了一致性可接受水平．整体来看，2022年和2021年新高考数学Ⅰ卷的知识深度一致性均较好．

3.3 知识广度一致性分析

知识广度一致性是要检验课程标准中希望学生所要学习的知识范围与学生正确做答评价试题或评价活动所需要的知识范围是否相同或者相当的．韦伯认为测量学生知识时，某条内容标准所对应的内容领域至少应该有超过50%的知识领域被测验到．

2022年和2021年新高考数学Ⅰ卷知识广度一致性分析如表3所示．

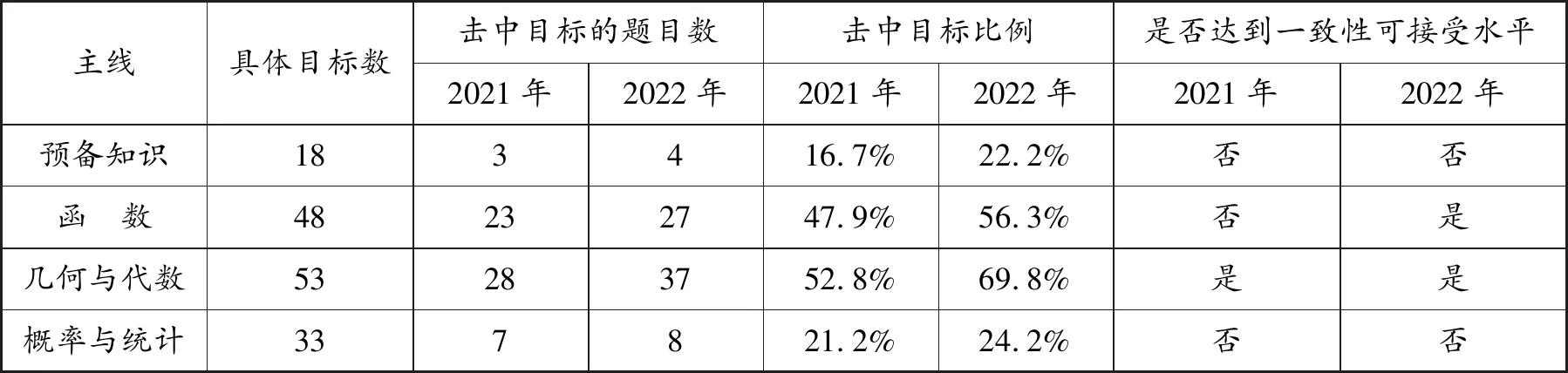
表3 新高考数学Ⅰ卷知识广度一致性分析

从表3中可以发现，2021年新高考数学Ⅰ卷的预备知识、函数和概率与统计三个主线击中的题目数均未达到知识广度的一致性可接受水平；几何与代数部分击中的题目达到了知识种类的一致性可接受水平．整体来看，2021年新高考数学Ⅰ卷知识种类一致性较差．而2022年试卷中四个主线击中的题目数所占知识领域的比例相比2021年试卷均有一定程度的上升，尤其是函数主线，2022年试卷已经达到了一致性可接受水平．相比之下，2022年新高考数学Ⅰ卷的知识广度一致性略好．

3.4 知识分布一致性分析

知识分布平衡性研究的是某一内容标准被命中的目标数量，不考虑没有命中的目标如何分布．该指标用来表示与其他目标相比评价更为重视某一目标的程度．

其平衡指数的公式为：

其中O表示被命中的某内容标准所包括的目标总数；Ik表示命中目标的试题数；H表示命中该内容标准的试题总数．韦伯认为平衡指数大于或等于0.7时，说明试题较均匀地分布在各个目标上．

2022年和2021年新高考数学Ⅰ卷知识分布一致性分析如表4所示．

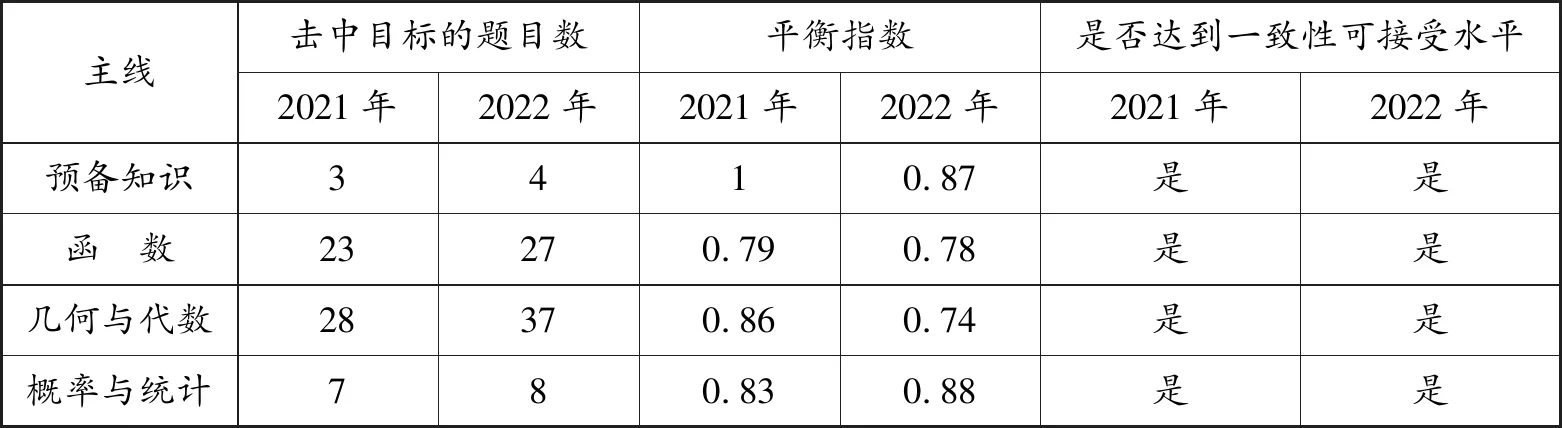
表4 新高考数学Ⅰ卷知识分布一致性分析

从表4中可以发现，两年试卷的四个主线知识平衡指数均大于0.7，即两年试卷均达到了一致性可接受水平．整体来看，2022年和2021年新高考数学Ⅰ卷的知识平衡一致性均较好．

4 结论

4.1 知识种类一致性研究结果分析

课程标准中对于四大主线在必修和选择性必修课程的总课时分配建议是：预备知识18课时、函数82课时、几何与代数86课时、概率与统计46课时．从课时分配上我们可以看出，预备知识所占课时最少，是因为该部分为初中数学知识到高中数学知识的过渡内容，旨在使教学模式得到优化以及引导学生感悟高中数学课程的特点，故考虑到高考试卷题目和时间的有限性，直接考查该部分知识的试题较少[1]．虽然两年试卷的概率与统计主线均达到了一致性可接受水平，但两年分别击中了7道题和8道题，均占该主线总体的比重较低．

4.2 知识深度一致性研究结果分析

我们发现，两年的试卷在函数和几何与代数两个主线部分均有较大比例的高于目标要求的试题出现，函数和几何与代数这两部分内容在整个高中数学知识中占比最大，故高考试题中对这两部分考查的角度较广、深度较大，会有高于课程目标要求的题目出现．同时我们发现四个主线的题目均未出现低于课程目标的题目，说明高考更注重应用能力的考查．

4.3 知识广度一致性研究结果分析

研究结果表明，2021年试卷只有几何与代数主线达到了一致性研究水平，说明2021年试卷在其余三个主线有多道题目考查了相同的知识点，导致了虽然命中较多题目但考查的知识点仍不够全面的局面．2022年试卷在2021年的基础上函数主线的试题达到了一致性可接受水平，体现了新高考数学Ⅰ卷的题目正朝着考查广泛知识点方向转变的特点．我们知道，高考作为整个高中阶段的学业评价，如果考查的知识点过于集中会导致评价的信度降低．

4.4 知识分布一致性研究结果分析

试题的知识分布均匀，能够有效地检验出学生对知识点的整体掌握情况．两年的试卷均体现了文理不分科的新高考政策下试卷的整体难度高于旧高考文科，而低于旧高考理科．

总体来看，2022年和2021年新高考数学Ⅰ卷与课程标准的一致性较好，试题很大程度上符合课程标准中要求的知识能力和认知水平，能为高校招生提供有效的依据．

5 建议与展望

5.1 对一致性测评工具的建议

韦伯模式在一致性可接受水平的界定上存在一些不明确的地方，比如知识种类一致性的判断是要求至少6次命中某一条标准的内容，其一致性才可以接受，而对于课标中所含目标数量较大的主线，如果试卷命中的题目大于6道，但占总目标数比例较小时，其可信度和参考价值就会大幅降低．比如本研究中两年试卷的概率与统计主线部分．

5.2 对一线教师的建议

课程标准是国家的纲领性文件，它作为一种期望课程，不仅对课程内容做出了明确规定，也对高中生提出了具体的要求，同时它也是高考试卷编写的依据．所以一线教师应该仔细研读课程标准，有针对性地进行教学活动．2022年和2021年新高考数学Ⅰ卷中均出现了一定比例的高于课程标准要求的题目，故教师在教学过程中应注重对学生六大数学核心素养的培养，更倾向学生知识和技能的运用，不只是为了教学而教学．

5.3 对高考试题编者的建议

虽然新高考开始实行选科制度，但是也不能只是简单地将原来旧高考模式下的文理科数学试卷进行整合，而是应该对题目进行合理的分配[2]．课程标准中用大量篇幅陈述了数学建模的意义，也为数学建模课程安排了相应的课时，故试卷编写的过程中应该将建模思想考虑进去，同时题目要更注意实际背景，贴近生活．