基于自适应轮动归类的微震震相识别方法

贾宝新，李峰

辽宁工程技术大学 土木工程学院，辽宁阜新 123000

0 引言

随着矿山开采深度及规模的增加，开采所处地下环境的不确定性逐渐增强，表现为所处地层的原生地质构造易遭受大范围扰动甚至破坏，导致矿产资源在开采的同时也会伴随着一些诸如冲击地压、采空区垮落、岩爆、巷道片帮冒顶等环境与安全隐患(潘一山等，2007；崔峰等，2019；李金雨等，2019).矿产资源开采过程中普遍采用微震监测技术对灾害源进行监测定位，其中微震震相识别方法是微震监测的核心内容，也是实施实时微震监测以及间接提高灾害预测精确度的关键(陈泽等，2020；Yu et al.，2020).

微震震相识别方法主要是利用微震信号本身的频率、功率密度、持续时间、振幅等属性(贾宝新等，2021)，将其中包含的微震响应与背景噪声进行区分，使得微震响应可以被自动识别并截取.针对微震响应识别困难的问题，董陇军等(2016)选取微震力矩对数、能量对数、传感器触发数量、首次峰值幅值对数等属性作为Fisher分类法的特征参数，以此训练震相识别模型；朱权洁等(2013)提出了可利用到时、振幅等信息剔除异常波形的多通道微震联合识别方法；姜福兴等(2014)提出了一种将预处理与识别后再优化相结合的微震单事件多通道联合识别方法；Chen和Paul(2021)提出了利用量化角频率、地震矩、应力降等震源特性，对微震爆破事件实施自动识别和鉴别的方法；赵明等(2019)利用真实余震事件和深度学习卷积神经网络(CNN)进行模型训练，以此对地震波形进行了分类与识别；Zhao等(2015)将微震波形重复性、尾波下降、信号主频和发生时间作为Fisher分类法特征参数，以此训练震相识别模型；Dong等(2016)选取微震发生时间、地震矩、总辐射能、S波和P波能量比、拐角频率和静态应力降作为微震识别的特征参数，并用Fisher分类法、朴素Bayes法和逻辑回归进行分类；Jiang等(2021)通过奇异值分解减少数据量后，利用微震信号时频特性提出了基于随机森林分类器的震相识别方法；Wu等(2016)提出了基于S变换、相位和频率的相似性以及随机组合分析P波波形的震相识别方法；Zhang等(2019)提出了一种集成经验模态分解(EEMD)、奇异值分解(SVD)和极限学习机(ELM)相结合的震相识别方法.

以上研究成果在一定程度上提高了震相识别的准确率，但也存在一些不足.例如改进长短时窗法(short time-window average/long time-window average，简称STA/LTA)必须计算整段信号的长、短时窗比值，而整段信号中无效的背景噪声占绝大部分，故其浪费了大量的算力与时间；机器学习方法通常面临样本量不足的问题，导致其难以处理多种形式的微震信号；多参数分析法由于其特征参数复杂，导致参数匹配难以普适，方法的实际应用较为困难.

针对以上问题，本文基于自适应高通滤波、背景噪声幅值上下界计算、轮动圆半径计算及轮动迭代、超限点归类分组4个信号处理流程提出了自适应轮动归类法，并通过分别对模型试验与实际工程中所得的微震信号进行震相识别，证明了自适应轮动归类法相较改进STA/LTA方法在识别准确率、识别稳定性、计算速度、计算稳定性等方面均具有一定的优势.自适应轮动归类法针对目前已有震相识别方法存在的问题提出了可行的解决方案：相较改进STA/LTA方法，该方法只需对微震信号幅值超出限定范围的超限点进行归类分组，分组结果即为震相识别结果，而不必遍历整段信号并筛选出超出阈值的部分信号，以此节省了算力，又因其只关注数据点是否超出轮动圆范围，而不需考虑超出部分的具体数值，因此避免了长短时窗相比必须在阈值限定范围内的普适性不佳的问题；相较机器学习方法，该方法不需要大量且形式各异的样本信号进行模型训练，其自身的自适应高通滤波步骤可将不同形式的微震信号滤波为微震响应较为突出的信号形式，随即以此为基础并通过之后的处理步骤对微震响应进行识别；相较多参数分析法，该方法需要主动调试的初始赋值参数仅为3个，分别为分组间隔Fint(s)、范围扩大系数Q以及采样间隔Cint，并且其取值方法独立且定义明确，不需要多次尝试寻找最优组合，因此该方法在保证识别质量的前提下也可适应广泛的应用场景.

1 自适应轮动归类法基本原理

利用背景噪声与微震响应之间的关系，自适应轮动归类法可以从微震信号中筛选出微震响应，其原理是先计算可涵盖绝大部分背景噪声的特征值，再以该值的系数倍为界限找出大于该界限的所有微震信号数据点，即超限点.最后以一定的标准对超限点进行分类，所得结果即为震相识别结果.

1.1 自适应轮动归类法运行原理

自适应轮动归类法包含以下4个主要步骤：

(1)自适应高通滤波

为了降低背景噪声对于微震响应的干扰，并提高自适应轮动归类法的识别准确率与算法稳定性，需对原始信号进行高通滤波，而高通滤波所需的高通滤波下限需要人工输入，故为了实现整体方法的自动流程化运行，需要一种可以处理多种形式微震信号的自适应高通滤波处理方法.本步骤由自适应高通滤波下限计算以及对原始信号进行高通滤波两部分组成，其中后者采用Matlab软件中的巴特沃斯滤波器实现，以下主要说明由本文提出的自适应高通滤波下限的计算方法.

背景噪声通常由多种不同频段、不同能量的噪声信号组成，本步骤是以其中能量较大且频率稳定的噪声为准，利用高通滤波过滤该频率及以下的信号，以此保留较高频率的微震响应信号以及一部分高频率但能量低的噪声信号，用以将原始信号中的微震响应信号凸显出来.从原始信号中随机筛选出时长相同但起始时刻不同的多段截取信号，通过计算各截取信号的基础过零率并将其中位数作为整段信号中背景噪声主频的估计值，以此获得高通滤波下限并对原始信号进行高通滤波.

针对高通滤波的自动化运行，本文提出了基础过零率，利用周期函数判别周期的方式(单位时间内自下而上穿过X轴次数)来估算截取信号中能量较高且频率稳定的主要趋势波形的频率.此估算频率对结果的精确度要求不高，因为随机截取多段信号中，其中可能包含微震响应、施工设备响应等干扰信号，并且背景噪声在整段信号中的占比是最大的，所以为了减小误差并找到目标背景噪声，需要截取多段信号并取其基础过零率的中位数，以保证所得结果可以代表微震信号中能量较高且频率稳定的背景噪声.

截取信号段数即分样组数Ldz计算见后(5)式所示，基础过零率计算方式如图1所示，图中10 s内信号自下而上穿过X轴次数为9次，故基础过零率为0.9 Hz.

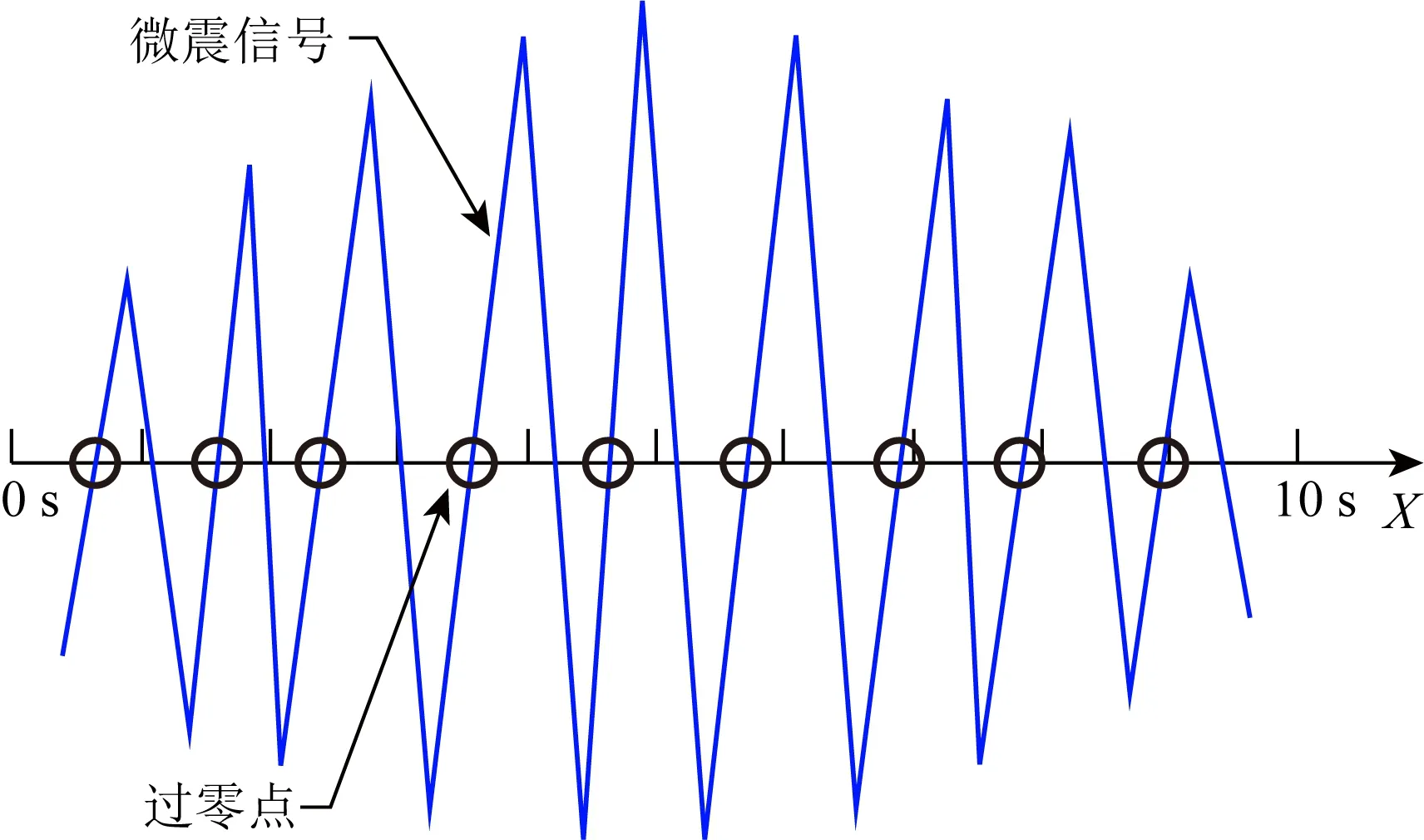
图1 基础过零率计算示意图

自适应高通滤波前后的语谱图对比如图2所示.可见图中288.018 Hz以下的低频背景噪声已被准确过滤，图中使用的微震原始信号及其自适应高通滤波效果如图3所示.

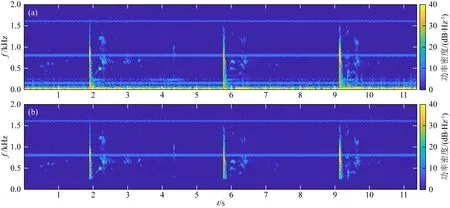
图2 自适应高通滤波前后的语谱图对比

(2)背景噪声幅值上下界计算

为了进一步凸显出微震响应信号并初步确定轮动圆半径Rw的取值依据，需要找到可以基本涵盖全部背景噪声幅值的范围，确保此范围内基本为背景噪声，而范围外基本为微震响应，此范围的上界与下界即为背景噪声幅值上下界.

在原始信号经过自适应高通滤波提高信噪比后，引入正态分布中横轴区间(μ-2σ,μ+2σ)的落点概率95%作为信号的无效置信区间，利用自Y=0逐步增加涵盖范围并判断是否已包含整段信号中95%的数据点的方法，迭代比较出满足上述条件的背景噪声幅值上下界，确保所得结果可以涵盖大部分背景噪声及无效响应并初步筛选出微震响应信号.

为了更好的适应不同信号特征变化，规定算法采集微震信号时间间隔Tcol(s)为

Tcol=|--[Fint/(1-95%)]/10⎤×10，

(1)

该公式限定了采集微震信号时间间隔Tcol为10的倍数，其最小值为10 s，并且可以根据具体的微震响应持续时间以10的倍数进行调整.这样不仅保证了微震响应时长较短情况下算法的适配性，也可适应诸如矿震、地震等微震响应时长较长的情况，方便了后续的算法计算.

自适应高通滤波与背景噪声幅值上下界计算示意图如图3所示.

图3 自适应高通滤波与背景噪声幅值上下界计算示意图

(3)轮动圆半径计算及轮动迭代

为了筛选出少量可代表单次微震响应的较高幅值数据点，为下一步超限点归类分组提供基础数据，使用轮动圆半径Rw组成的轮动圆自整段信号的起点时刻至终点时刻，遍历所有数据点并筛选出幅值大于轮动圆半径Rw的数据点，即超限点.

少量且有较高幅值的数据点有利于归类分组，而且可以较为突出的区别于背景噪声，因为较高幅值数据点是由能量突变的微震响应所造成的，其可区别于全程存在但能量较低的背景噪声，并且由于能量的突变，微震响应区域的幅值要高于背景噪声区域且所含数据点要少于背景噪声区域，所以筛选出少量且幅值较高的数据点更加符合微震响应的特征.

轮动圆圆心位于X轴上，其半径取值为背景噪声幅值上界Du与背景噪声幅值下界Dd间的距离的范围扩大系数Q倍，通过遍历整段信号所有数据点并与其进行比较，筛选出大于轮动圆半径Rw的数据点，即可获得下一步骤所需的所有超限点.迭代筛选时采用整段信号中前后两个元素绝对值的平均值来代表此处信号的幅值，这样可以增加迭代比较的适用范围，避免出现单个数据点激变导致的识别错误.轮动圆半径Rw的计算公式如式(2)所示，超限点筛选条件如式(3)所示，轮动圆筛选超限点示意图如图4所示.

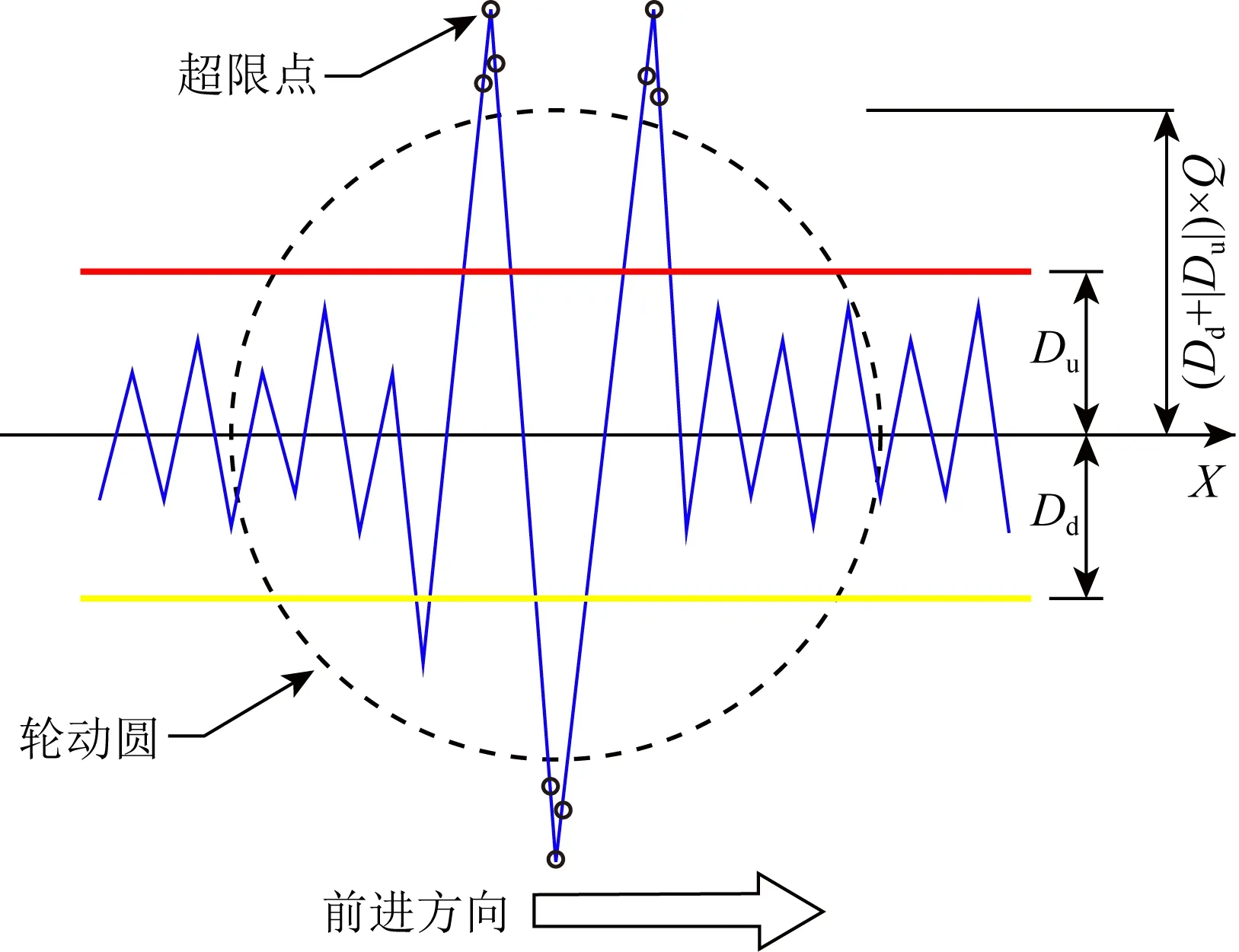
图4 轮动圆筛选超限点示意图

(4)超限点归类分组

为了最终获取微震信号中微震响应的影响区域即对整段微震信号进行震相识别，需要将轮动圆筛选出的超限点进行归类分组，分为同一组代表一次震相识别结果，分为多组则代表多次震相识别结果.

超限点作为微震响应的代表少量分布于整段微震信号中，由于不同次微震响应之间存在一定的时间差，所以可以利用一个较大的时间间隔对超限点进行归类分组，若多个超限点之间的时间间隔不超过规定的时间间隔，则可分为一组，此组即为一次震相识别结果.轮动圆半径计算及轮动迭代步骤中选出的全部超限点，将其按分组间隔Fint进行归类，若前后两者之间的时间差大于分组间隔Fint则归为一类，反之归为下一类，如是选出所有类，即为所求震相识别结果.超限点分类效果(自适应高通滤波后)即自适应轮动归类法识别震相效果如图5所示，图中红色点划线矩形框为震相识别结果.

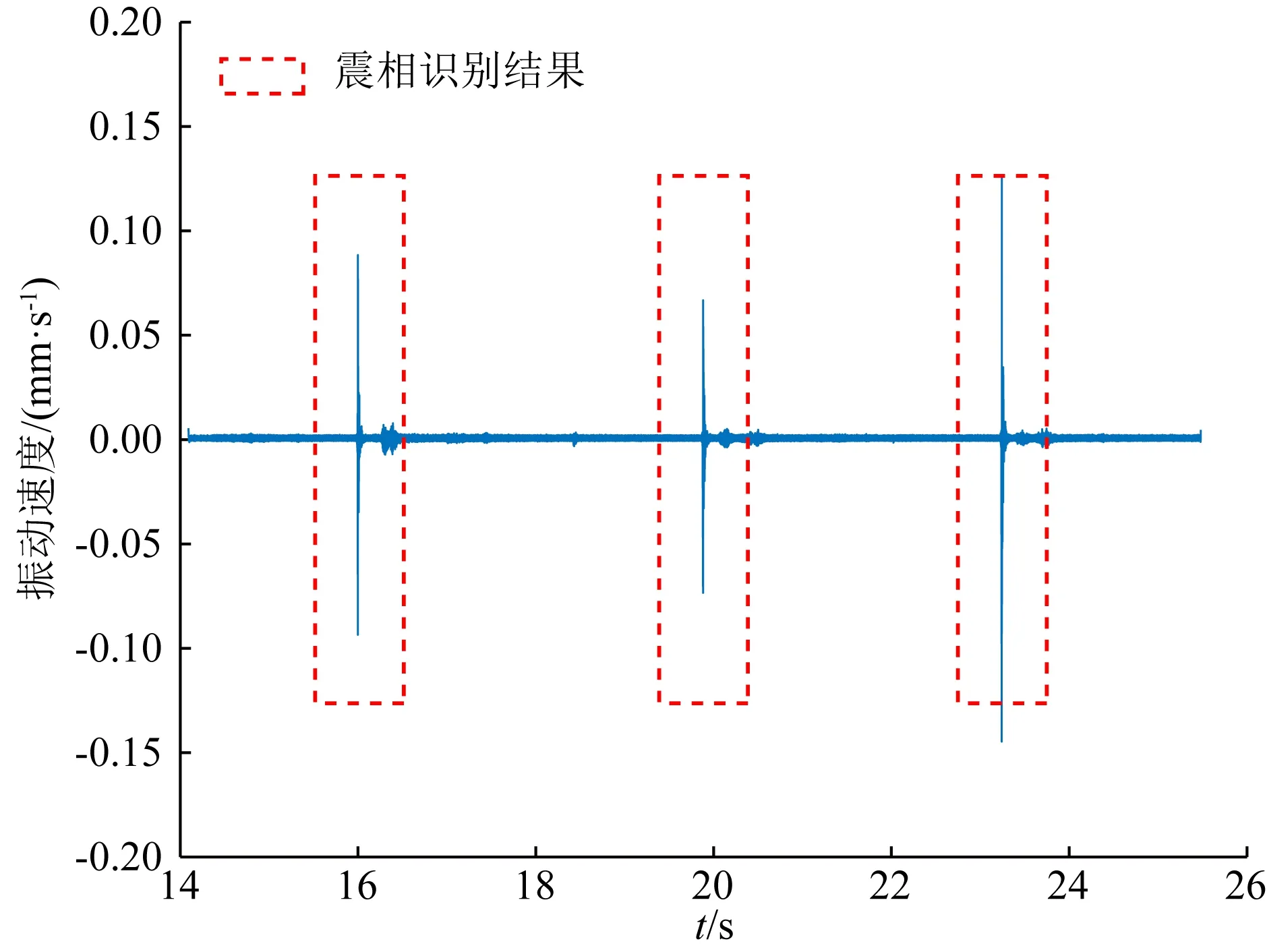
图5 超限点归类分组效果示意图

1.2 自适应轮动归类法的实现

(1)算法主线运行流程

① 读取微震信号数据S2(mm·s-1)与对应时间数据S1(s)，并执行②.

② 输入以下数据：

采样频率Fs(Hz)，采样间隔Cint，分组间隔Fint，范围扩大系数Q=2，背景噪声幅值上界Du=0，背景噪声幅值下界Dd=0，并执行③.

③ 按照采样间隔Cint对微震信号数据S2与对应时间数据S1进行数据规模缩减，并执行④.

④ 计算自适应高通滤波下限Hp(Hz)，随后将所得结果作为高通滤波下限对微震信号数据S2进行高通滤波，并执行⑤.

⑤ 计算微震信号数据S2升序排列中前95%的元素个数并将其赋值给过滤总数Jnum，并执行⑥.

⑥ 将0赋值给计数因子j，依次判断微震信号数据S2内元素是否同时满足小于背景噪声幅值上界Du且大于背景噪声幅值下界Dd，若满足将j+1赋值给计数因子j，否则执行⑦.

⑦ 判断计数因子j是否大于过滤总数Jnum，若满足执行⑨，否则执行⑧.

⑧ 将Du+1赋值给背景噪声幅值上界Du，将Dd-1赋值给背景噪声幅值下界Dd，并执行⑥.

⑨ 计算轮动圆半径Rw并依次判断其是否满足以下公式：

Rw=(Du+|Dd|)×Q,

(2)

Rw<(Ji+Ji+1)/2,

(3)

式中：i为索引序数，取值为1至微震信号数据S2的最大元素个数；Ji为迭代因子，表示微震信号数据S2中第i元素个元素的绝对值.

若满足将迭代因子Ji的值赋值给待归类矩阵P1的第i个元素，否则将0赋值给待归类矩阵P1的第i个元素，并执行⑩.

(2)自适应高通滤波下限计算运行步骤

① 读取微震信号数据S2与对应时间数据S1，输入采样频率Fs，并执行②.

② 计算分组间隔内元素总数Lint，并执行③.其中分组间隔内元素总数Lint满足以下公式：

Lint=|--Fint×Fs⎤,

(4)

③ 计算分样组数Ldz以及微震信号数据S2内元素总个数Gm，并执行④.其中分样组数Ldz满足以下公式：

Ldz=⎣(Send-Sfirst)/(1/|--(Fs/Lint)⎤)_|,

(5)

式中，Sfirst为对应时间数据S1中的首个元素的值(s)；Send为对应时间数据S1中的末尾元素的值(s).

④ 计算出Ldz组时间索引数a1(s)与信号索引数a2(mm·s-1)，并将时间索引数a1的值赋值给分组矩阵P3第1行中对应位置处的元素，将信号索引数a2的值赋值给分组矩阵P3第2行中对应位置处的元素.其中a1与a2满足以下公式：

a1=⎣Rand×Gm_|,

(6)

a2=a1-(Lint-1),

(7)

式中，Rand为0至1范围内的随机数.

⑤ 依次判断分组矩阵P3每组数据中的信号索引数a2是否小于1，若满足则执行⑥，否则执行⑦.

⑥ 按照式(6)与式(7)重新计算该组数据，直至信号索引数a2大于1，随后将计算结果赋值给分组矩阵P3对应位置处的元素，并执行⑤.

⑦ 依次将分组矩阵P3中每组信号索引数a2与时间索引数a1索引微震信号数据S2与对应时间数据S1中的各部分数据记录在数据记录矩阵P4中，并执行⑧.

⑧ 依次判断数据记录矩阵P4中每组数据中的微震信号数据的前后两个元素是否满足前者小于0且后者大于0，并统计出每组数据中满足条件的元素的总个数，将其赋值给过零率记录矩阵P5中对应组号的元素，并执行⑨.

⑨ 将过零率记录矩阵P5中的每个元素除以其对应时间数据的总时长，随后计算出过零率记录矩阵P5的中位数，即为所求的自适应高通滤波下限.

自适应轮动归类法流程图如图6所示.

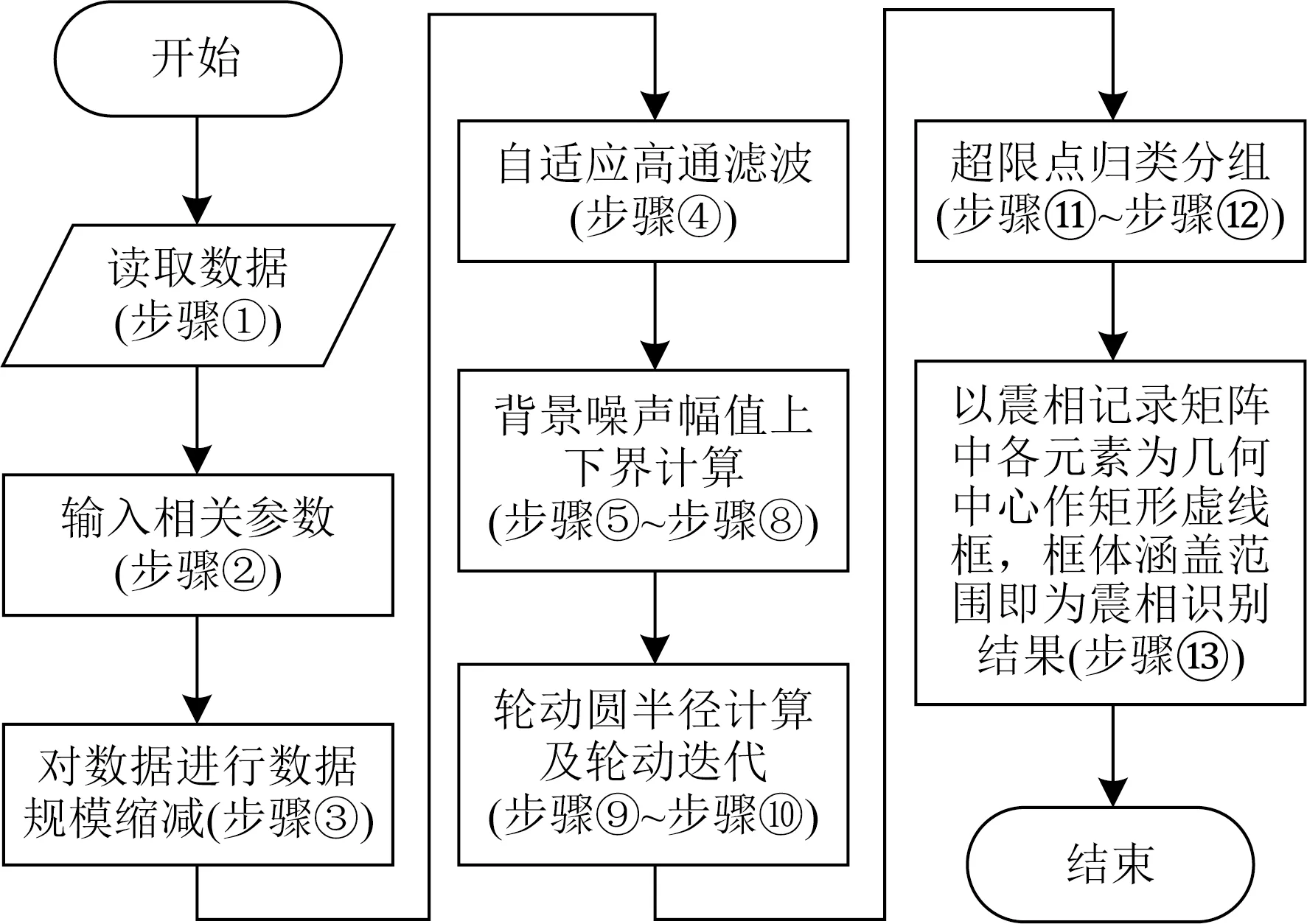
图6 自适应轮动归类法流程图

1.3 自适应轮动归类法初始参数分析

本算法需要初始赋值的参数共有4个，分别是采样频率Fs、采样间隔Cint、分组间隔Fint、范围扩大系数Q.

(1)采样频率

采样频率Fs据由监测设备决定，后续数据处理操作不可对其进行更改，根据已有研究成果(贾宝新等，2017；贾宝新和李峰，2022)，采样频率Fs越大，可捕获的微震响应细节越多.

(2)采样间隔

采样间隔Cint用于对信号进行规模缩减，比如间隔10个数据点采样一次，采样间隔Cint即为10.这种缩减虽可通过减少计算量实现大幅提高计算速度，但却会使原始信号的细节减少，由于微震响应信号持续时间较短，这种采样方式容易漏掉振幅等关键点.故采样间隔的选取应当根据震相识别整体的计算速度来进行调整，应当在保证震相识别全过程计算时间小于截取信号时长的前提下进行调整，这样既能满足实时监测的要求，又能保证原始信号细节的不丢失.

(3)分组间隔

分组间隔Fint用于对超限点进行分组，该值的选择可根据微震响应持续时间来进行规定，比如钢球撞击室内试验模型产生的微震响应信号时长约为0.1 s(自子波振幅激变至恢复平稳状态)，便可将分组间隔Fint设置为0.1 s.若是工程实际的微震响应信号，可通过试测或者统计之前的微震持续时间，以此确定分组间隔Fint的选取，比如实测辽宁某煤矿矿震产生的微震信号持续时间约为10 s，此时分组间隔Fint便应当取值为10 s.

微震响应信号中凡是幅值大于轮动圆半径Rw的数据点均会被筛选出来，所以在较高采样频率下，代表同一微震响应的超限点数量是众多的，它们之间的时间差远小于微震响应整体的持续时间.故分组间隔Fint的选取其实并不敏感，只需确定不同工况下微震响应大致的持续时间即可.

(4)范围扩大系数

范围扩大系数Q用于扩大由背景噪声幅值上下界产生的背景噪声估计范围.因为95%置信区间的存在，可能有一部分非微震响应信号穿过此范围而被轮动圆筛选为超限点，从而被算法错误的认为是微震响应，故采用将背景噪声幅值上下界产生的背景噪声估计范围乘以范围扩大系数Q来进一步扩大轮动圆的筛选范围，所得结果即为轮动圆半径Rw.范围扩大系数Q可根据现场的信号干扰源的情况进行选取，该值的选取范围通常在1.0～3.0之间，若在实验室这种比较安静且背景噪声影响小的环境下，该值可取1.0，若有像放炮或大型工程器械震动干扰的情况下，该值可相应增大.该值的选取并不需要十分精确，对现场收集的微震信号进行试算识别后即可确认.

2 模型试验

震相识别的难点在于不同类型与不同组合的震相叠加导致难以采用明确的标准进行识别(金标，2020；贾宝新等，2020)，故现通过实验室搭建室内模型并采用人工发震的方式，对自适应轮动归类法的识别效果进行验证.

2.1 试验模型构建

利用石英砂、石膏、石灰、水以6∶3∶1∶2的比例混合后分层堆砌，构建室内模型，其尺寸为2.3 m×1 m×1.3 m.22个微震传感器在按设计位置嵌入墙体，其三维空间坐标如表1所示.图7中黑色球体与对应数字代表传感器位置与标号，黑色立方体与对应字母为震源位置与标号.

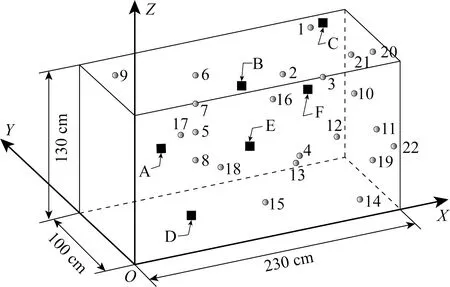
图7 试验布局图

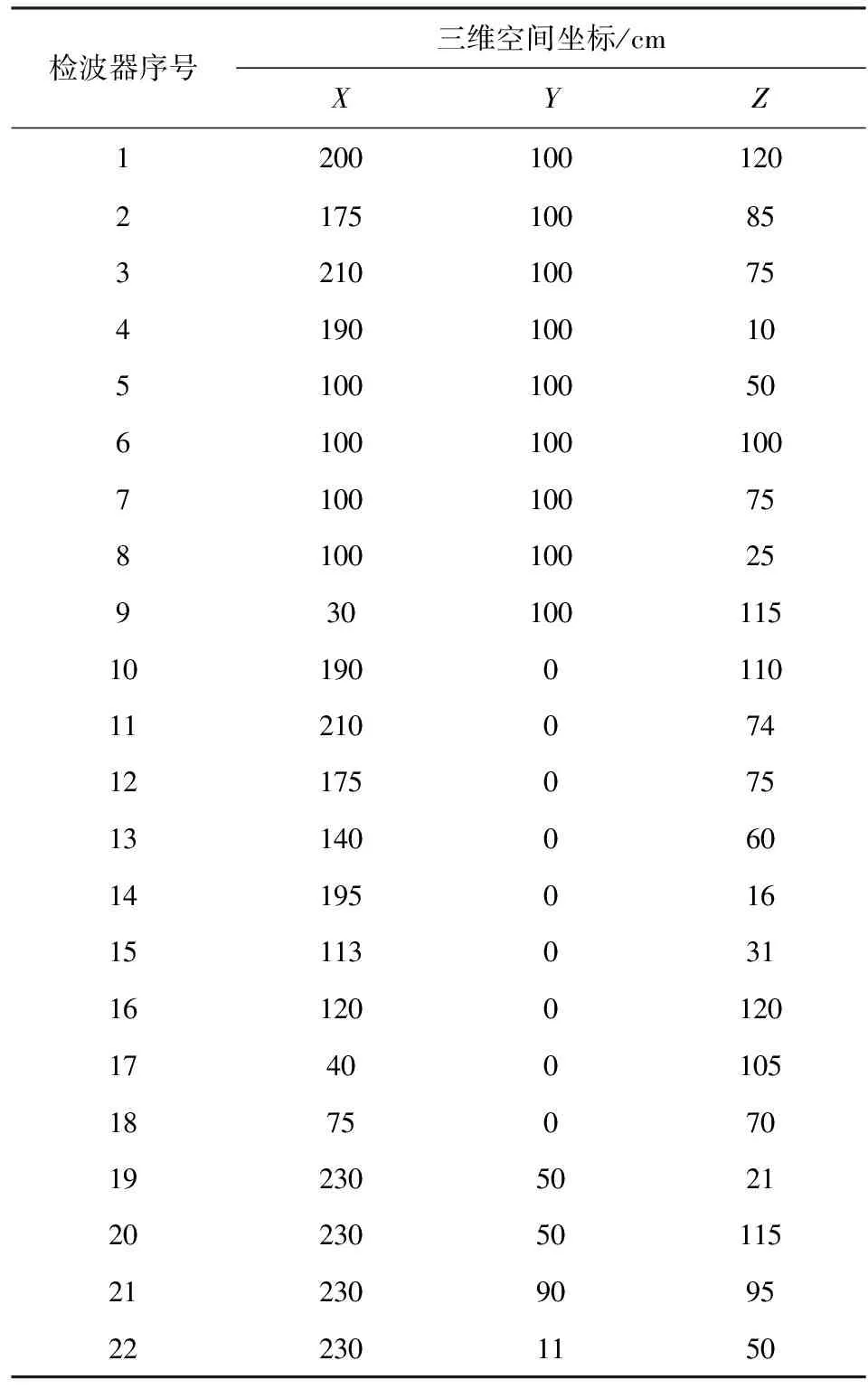
表1 各检波器三维空间坐标

2.2 监测设备

超高频多通道构造活动监测仪(Antenna-III)可监测频带宽度0～50 kHz的微震信号，其采样频率最高可达100 kHz.设备参数见表2，超高频多通道构造活动监测仪各组成部分见图8.

表2 超高频多通道构造活动监测仪设备参数

图8 超高频多通道构造活动监测仪

2.3 试验过程

模型搭建完成后带模具养护7天，每天定时洒水，以防止产生大的贯通裂隙.拆模后保持实验室通风且有每天至少5个小时的日照时间，照此持续30天且确保模型已干透后，随即可开始下一步试验.因模型干透后具有一定的脆性，所以当其被钢球撞击时会使表面产生一定的下陷与破裂，此现象可确保产生来自挤压破坏的P波以及来自剪切破坏的S波.

本试验采用半径1 cm的钢球对模型进行定长单摆撞击作为发震源，单摆定长为30 cm，固定铁架与钢球之间采用棉质线连接.钢球撞击位置分别为“震源A”至“震源F”，其三维空间坐标如表3所示.

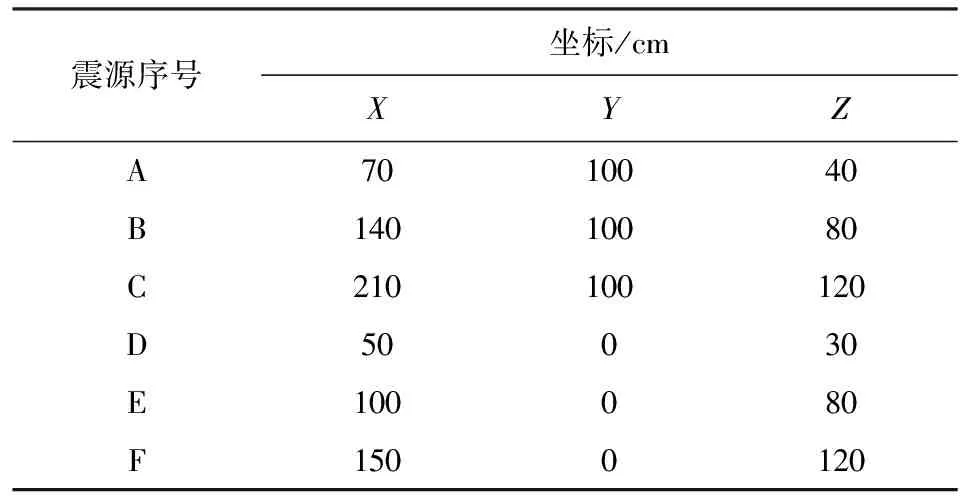
表3 各震源三维空间坐标

试验时先将钢球自然悬挂并刚好接触模型表面的指定撞击位置，随后将钢球拉至垂直于模型表面一定距离后放手，每间隔2 s左右进行1次撞击，以3次撞击为1次数据记录，形成1组包含由22个检波器产生的22段微震信号的数据组.每个震源点重复进行以上过程3次，产生3组共66段微震信号，试验现场照片如图9所示.

图9 试验现场

3 自适应轮动归类法识别效果分析

通过整理模型试验所得微震信号数据，共得到6个震源与22个检波器下不同信噪比的18组微震信号，即396段微震信号，其中每段信号包含3次微震响应.将1段信号作为一个整体对其包含的3次微震响应进行同时识别，若识别微震响应次数为3次，则算作1次成功识别.选取震相识别中常用的STA/LTA方法作为对照，通过二者在模型试验微震信号数据下震相识别效果的对比，对自适应轮动归类法的优越性进行验证.

3.1 定义微震信号信噪比

(1)计算原理

为区分信号质量并保证信号的合理分类，定义了微震信号专用的微震信号信噪比(Signal-to-noise ratio of microseismic signal，简称SNRmss)(dB).该值利用的是微震信号中震相信号振幅的平均值与自适应高通滤波过程中各截取信号振幅的最小值进行比较得出，相较传统信噪比定义该方法在背景噪声大小的界定上更为准确且适应性强.SNRmss由以下公式得出：

SNRmss=10×lg(Ssig/Snoi),

(8)

式中，Ssig为微震响应特征值，取值为微震信号数据S2中的震相信号振幅的平均值(mm·s-1)；Snoi为背景噪声特征值，取值为自适应高通滤波过程中筛选出的Ldz段截取信号振幅的最小值(mm·s-1).

图10a为各段截取信号的振幅大小，取其中位数即为Snoi取值，取微震信号数据S2中的微震响应信号振幅的平均值即为Ssig的取值，前者如图10b中黑色短划线所示，后者如图10b中绿色短划线所示，对比图中的原始微震信号可见二者能有效的代表背景噪声与微震响应.

图10 SNRmss原理示意图

(2)模型试验下SNRmss的计算及分析

计算模型试验所得微震信号数据的SNRmss，并对结果进行分类，所得箱型图如图11所示.图中横坐标代表的微震信号序号，例如“A-1”表示的是震源A下第1组微震信号，其中包含22个检波器采集的22段微震信号，每段微震信号包含3次微震响应.

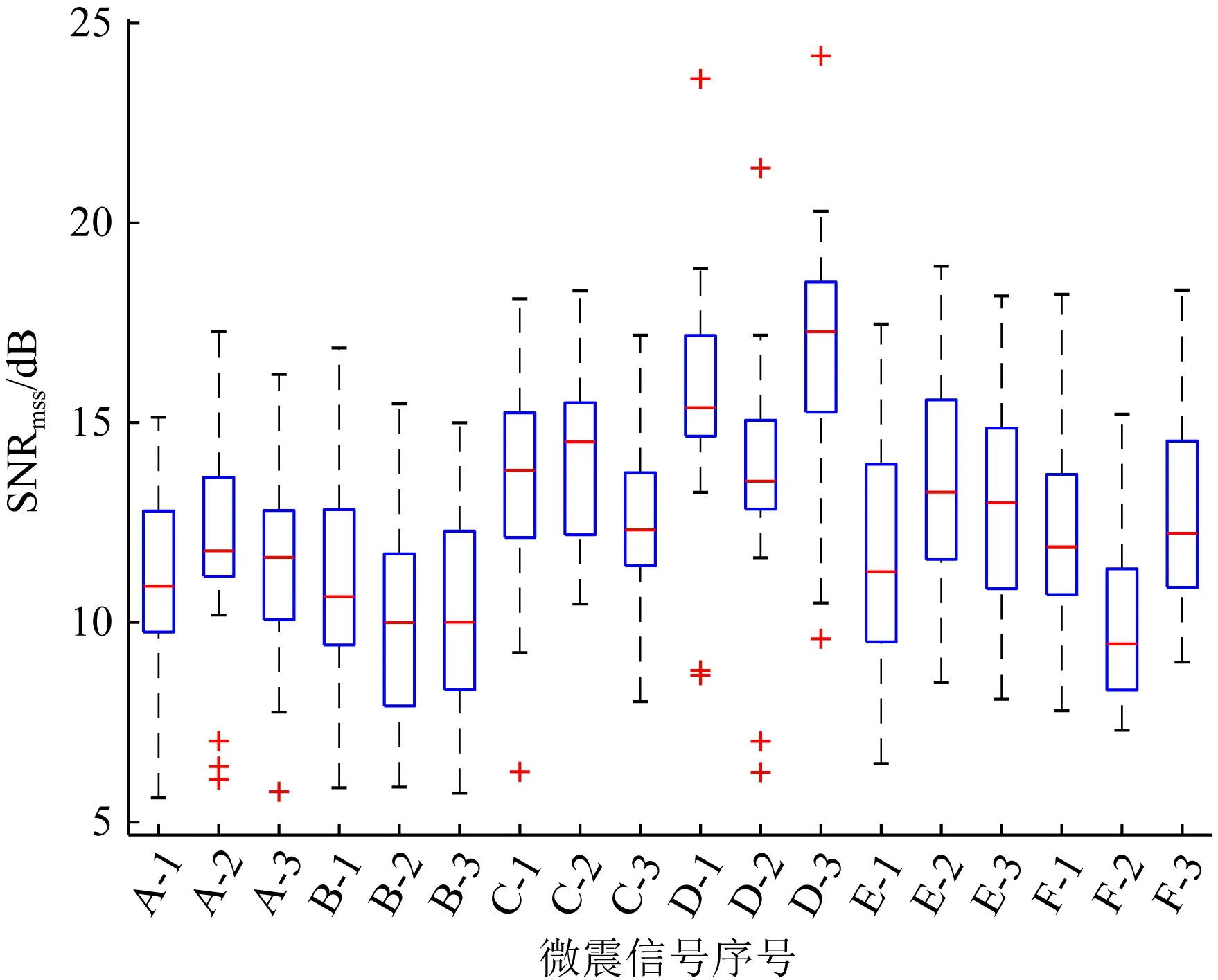
图11 模型试验下微震信号的SNRmss

自图11可知，模型试验中不同震源下微震信号的SNRmss的差别较大，以其中位数为代表，变化范围为0.099～7.818 dB，相同震源下微震信号的SNRmss的变化范围为0.012～3.744 dB，说明发震方式与监测环境对微震信号能否有效监测的影响较大.同时，SNRmss差别较大的试验信号也为下一步对两种方法震相识别效果的区分提供了有效条件.

3.2 改进STA/LTA方法数据分析

(1)STA/LTA方法原理及改进方法

作为一种判断信号瞬时响应的方法，STA/LTA方法常用于微震到时拾取及震相识别中.其中STA表征为微震信号因微震激励到达而产生的信号激变趋势；LTA表征为信号背景噪声的变化趋势(刘晗和张建中，2014).该方法的原理如下所示(刘晓明等，2017)：

(9)

(10)

(11)

式中，h为采样时刻(s)；p为时窗内迭代时刻(s)；Wl为LTA时窗(s)；Ws为STA时窗(s)；λ为响应阈值；CF(p)为微震信号在p时刻对应的特征函数值.

选择特征函数为微震信号的振幅绝对值在时窗内的叠加(贾宝新等，2021)，即：

(12)

(13)

(14)

式中，|A(p)|为p时刻微震信号振幅的绝对值.

因为STA/LTA方法只能筛选出信号幅值激变点而无法识别出震相，故将该方法与自适应轮动归类法中的超限点归类分组模块进行结合，组成改进STA/LTA方法.

(2)计算速度与识别偏差分析

定义识别偏差为每组微震信号识别结果与微震响应次数真值的差的绝对值和.

统计改进STA/LTA方法对各段微震信号进行震相识别所用的时间，随后对结果进行分析，统计结果如图12所示.

由图12可知，改进STA/LTA方法的计算时间在0.630 s至1.532 s之间，平均计算时间为0.869 s，并且图中每组数据之间的中位数与分布区间差别较大，表明该方法计算速度稳定性较差，即对不同类型的微震信号所用的计算时间差别较大.

图12 改进STA/LTA方法计算时间

使用改进STA/LTA方法对模型试验微震信号进行震相识别，识别震相次数结果如图13a所示.

由图13a可知，改进STA/LTA方法的震相识别结果波动性相对较大，有106段微震信号的识别次数出现了识别偏差，并且识别偏差幅度最大为3次，识别准确率为73.2%，识别偏差标准差为0.766，可见改进STA/LTA方法在识别准确率上欠佳，并且该方法的识别稳定性较差且偏差幅度波动大.

3.3 自适应轮动归类法数据分析

使用自适应轮动归类法对模型试验微震信号进行震相识别，识别震相次数结果如图13b所示.据图可知，该方法的识别结果相对稳定，有7段微震信号的识别次数出现了偏差，但识别偏差幅度最大仅为1次，识别准确率为98.2%，识别偏差标准差为0.133，可见自适应轮动归类法的识别稳定性与准确率均较为优秀.

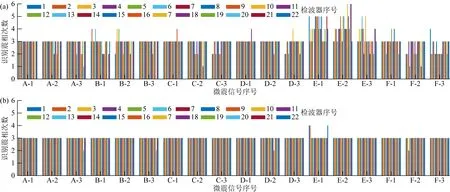
图13 模型试验下两种方法震相识别结果

统计自适应轮动归类法对各段微震信号进行震相识别所用的时间，利用箱型图对结果进行分析，统计结果如图14所示.

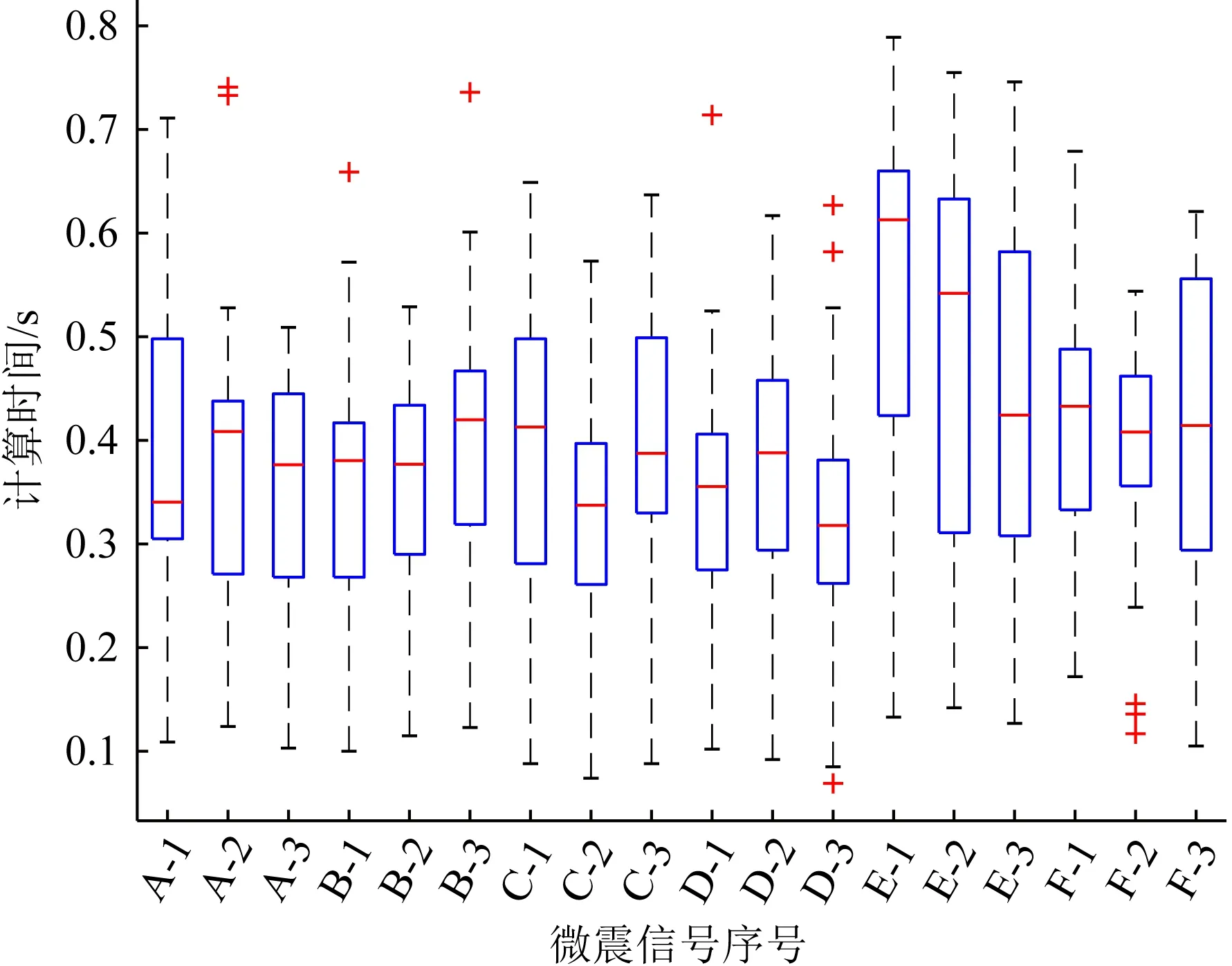
图14 自适应轮动归类法计算时间

由图14可知，自适应轮动归类法的计算时间在0.069 s至0.789 s之间，平均计算时间为0.384 s，并且图中每组数据之间的中位数与分布区间差别不大，表明该方法计算速度稳定性较好，即对不同类型的微震信号所用的计算时间较为稳定.

3.4 两种方法的震相识别效果对比

改进STA/LTA方法与自适应轮动归类法对于震相识别的效果对比如图13所示.试验中3次微震响应为1段信号，若3次均识别成功，记作1次成果的震相识别，由图13a可知，改进STA/LTA方法成功识别的微震信号为290段，因为数据总段数为396段，故其识别准确率为73.2%，同理可得自适应轮动归类法的识别准确率为98.2%.统计两种方法对模型试验数据的各项计算结果，所得二者在5项指标下的识别效果对比如表4所示.

由表4可知，模型试验所得微震信号数据下，相较改进STA/LTA方法，自适应轮动归类法的识别准确率提高了25.0%，识别偏差标准差为前者的17.4%，计算时间平均值为前者的44.2%，计算时间标准差为前者的67.4%.由此可见，自适应轮动归类法在识别准确率、识别稳定性、计算速度、计算稳定性等方面均优于改进STA/LTA方法.

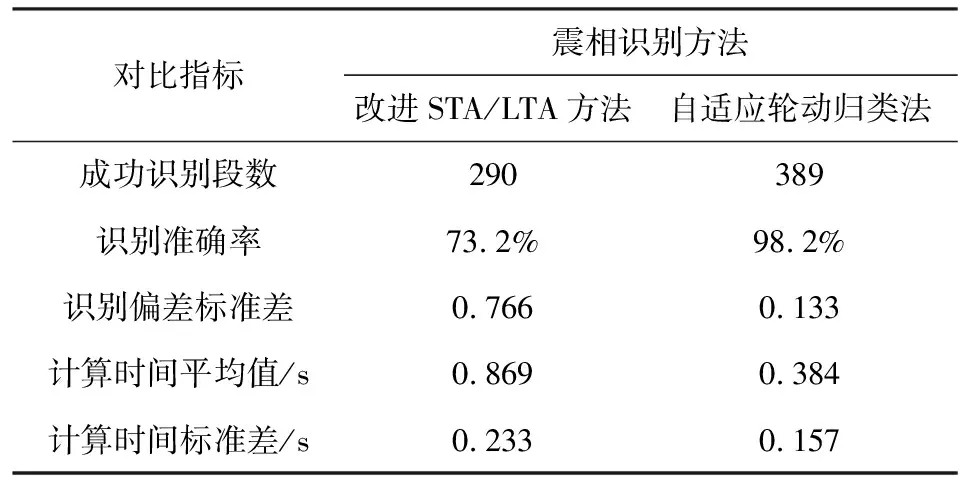
表4 模型试验下两种方法震相识别效果对比

3.5 影响因素相关性分析

计算两种震相识别方法对各组微震信号的识别偏差，计算结果与SNRmss的关系如图15所示.

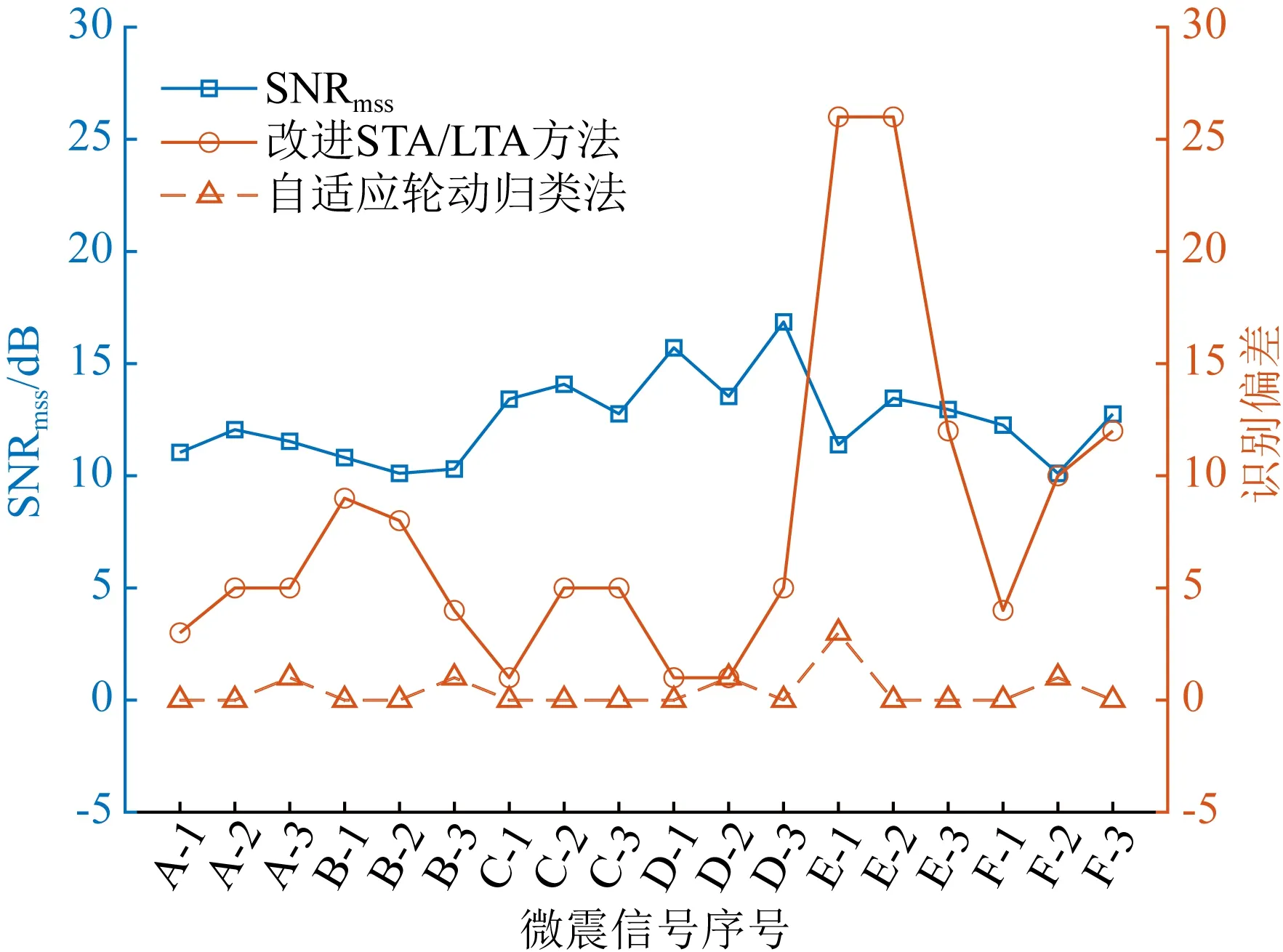
图15 SNRmss与识别偏差的关系

因监测设备的采样频率是固定的100 kHz，所以将信号长度定义为微震信号文件的大小，该值与计算时间的关系如图16所示.

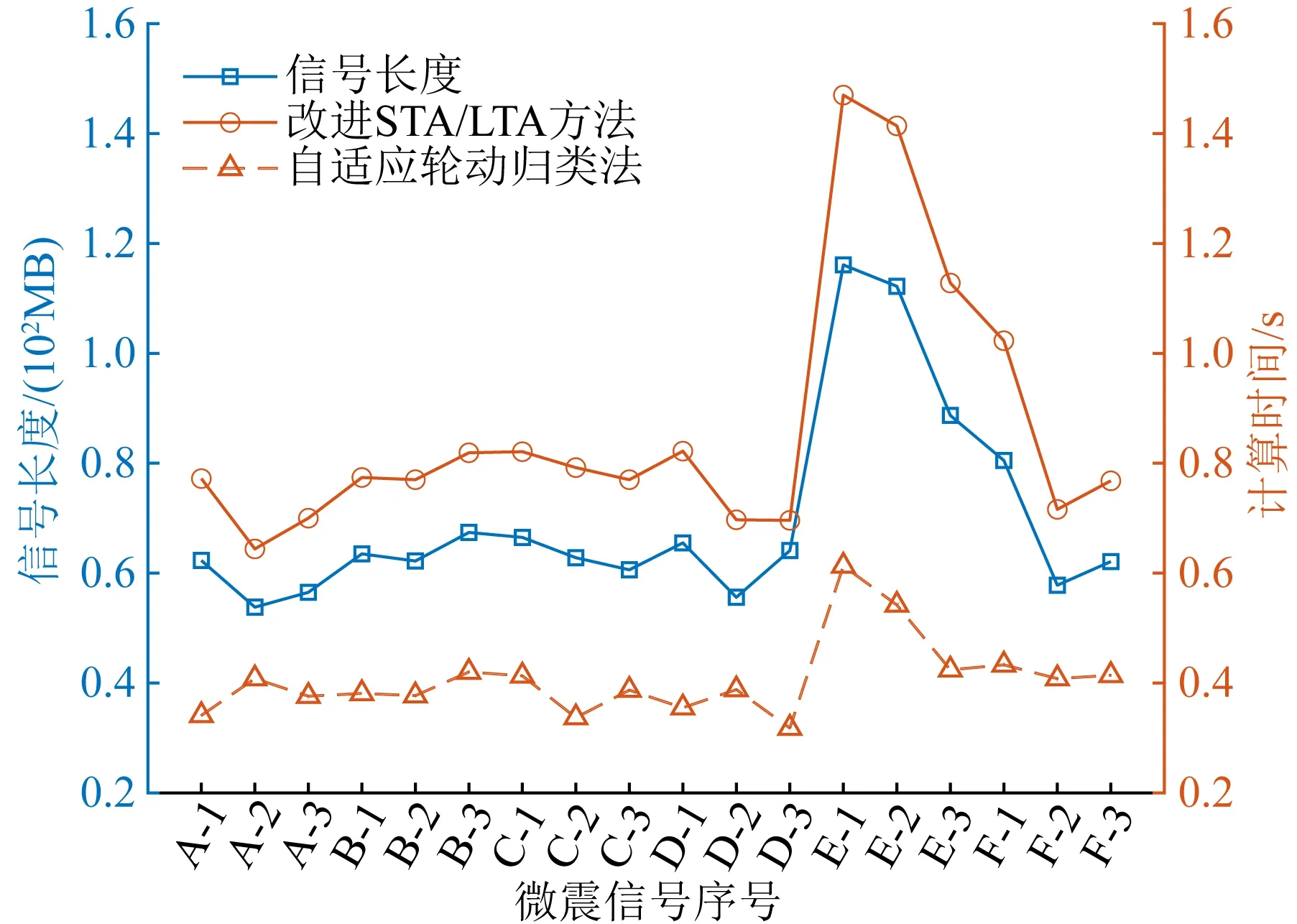
图16 信号长度与计算速度的关系

两种方法的计算速度与识别偏差和两项对比指标的相关性系数如表5所示.

由表5可知，改进STA/LTA方法的计算速度与识别准确率高度依赖于微震信号长度，而自适应轮动归类法则弱化了对该指标的依赖，其两项相关系数分别为改进STA/LTA方法的86.1%及47.8%，说明本文方法对比改进STA/LTA方法对信号长度的敏感度更低，可以保证对于长度不同信号的识别容错率与稳定性更高.

表5 两种方法的相关性分析结果

理论上信噪比越高，震相识别的准确率应当越高，但震相识别方法对于SNRmss的相关性也不宜过低或过高，若过低会导致方法的识别准确率忽高忽低，识别偏差难以掌握；过高会导致方法过于依赖高信噪比信号，使得面对因背景噪声振幅大且变化复杂的微震信号的适应性较差.然而实际工程中因为其他机械运作等原因，微震信号往往信噪比较低，对SNRmss有过高依赖性的方法往往无法投入实际使用.本文统计的识别偏差为单组微震信号中各段信号的识别偏差绝对值的总和，所以识别偏差应该与SNRmss呈负相关关系，故此本文以两项指标与SNRmss相关系数为-0.5为最佳，用以评判两种震相识别方法的效果.

自表5中可知，自适应轮动归类法的计算速度和识别偏差与SNRmss的相关系数较改进STA/LTA方法更为接近-0.5，说明本文方法对SNRmss的依赖性适中，而改进STA/LTA方法的两项相关系数接近于0，说明该方法识别偏差不稳定分布且后期识别准确率提升空间有限.

综上所述，自适应轮动归类法在处理信号上的容错率与稳定性较改进STA/LTA方法更高，并且能够更好的适应且不过度依赖高信噪比的信号，后期可通过软、硬件提高信号信噪比或者通过微震信号质量控制方法筛选高信噪比信号，使其进一步的提高震相识别的准确率.

4 工程验证

为了进一步验证自适应轮动归类法对于微震信号震相识别的可靠性，选取辽宁某煤矿微震监测工程中的微震信号进行验证.

4.1 微震监测工程介绍

辽宁某煤矿微震监测工程的目的是为预防矿井冲击地压等动力灾害，该项目共设置8个监测台阵，每个监测台阵布置1台三分向微震检波器，用以全天候监测矿区范围内发生的微震事件.将7次不同时期与不同发震位置的微震事件所产生的微震信号进行分类，将其震源分别命名为“震源I”至“震源O”，其中每次事件包含7个三分向检波器的X轴、Y轴、Z轴3个分向的微震信号，每个分向的微震信号包含1次微震响应，信号形式如图17所示.

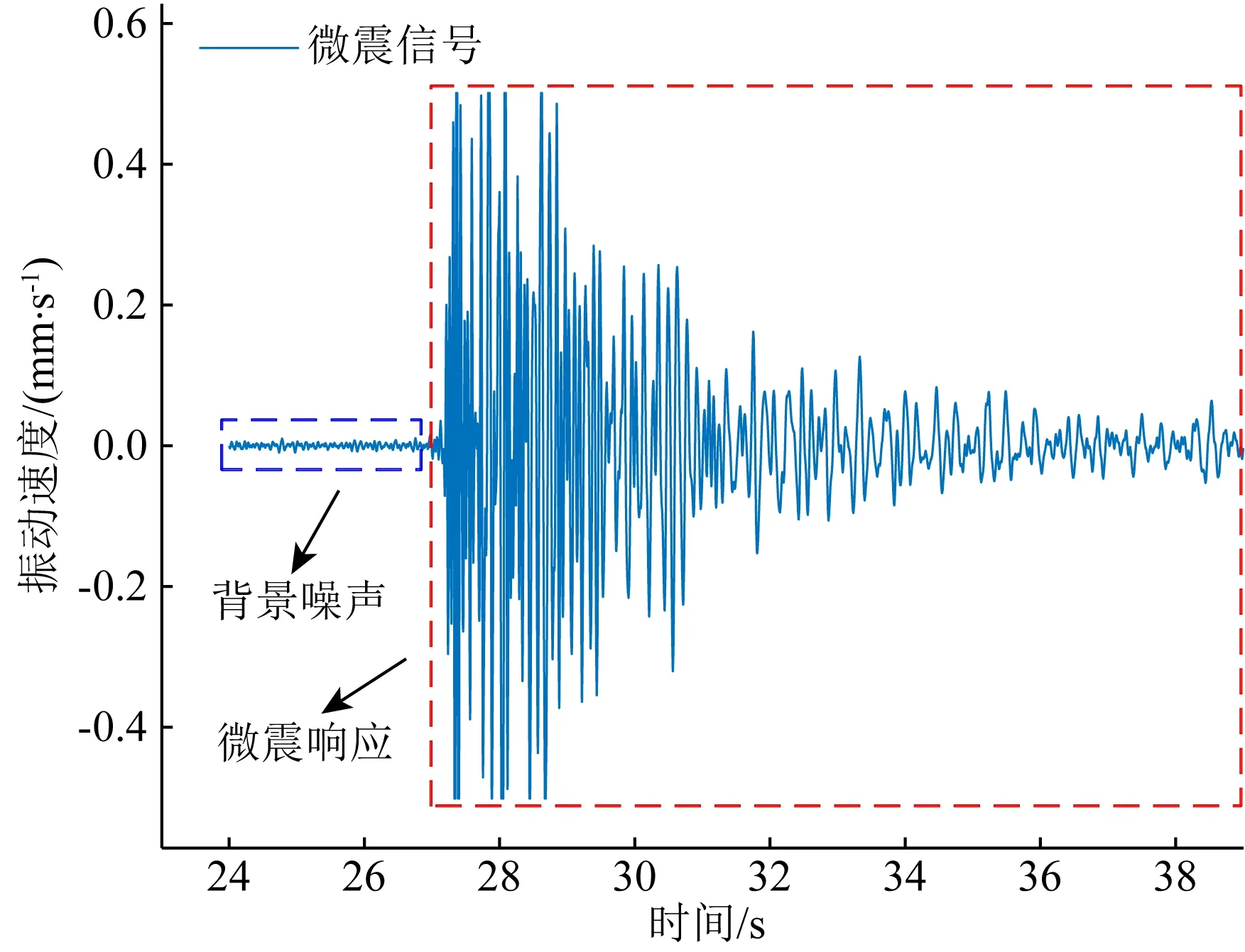
图17 微震监测工程中的微震信号示意图

4.2 两种方法的震相识别效果对比

下述分析中自适应轮动归类法采用初始参数：采样频率Fs=5000 Hz，采样间隔Cint=10，分组间隔Fint=10 s，范围扩大系数Q=2.

(1)识别结果分析

通过日常对矿区微震事件的监测，共收集到7个震源、8个检波器、3个分向的168段微震信号，将其用“震源-分向”的形式表示，例如“I-X”表示的是震源I下检波器X轴分向监测到的微震信号.利用改进STA/LTA方法与自适应轮动归类法对所有微震信号进行震相识别，其识别结果如图18所示，图中每个长方体代表1段微震信号，其中每段微震信号的微震响应次数真值为1次，纵轴识别震相次数代表的是对应震相识别方法识别每段微震信号所得的微震响应次数，识别震相次数与微震响应次数真值之间的差的绝对值称作识别偏差.

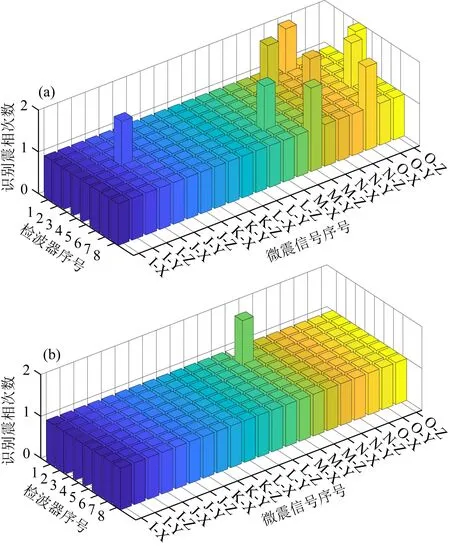
图18 两种方法的震相识别结果

由图18a可知，改进STA/LTA方法识别失败次数为9次，识别偏差幅度最大为1次，识别失败结果分布不规律.由图18b可知，自适应轮动归类法识别失败次数为1次，识别偏差幅度最大为1次.

(2)计算时间分析

统计改进STA/LTA方法与自适应轮动归类法对上述168段微震信号进行震相识别所用时间，所得结果如图19所示.

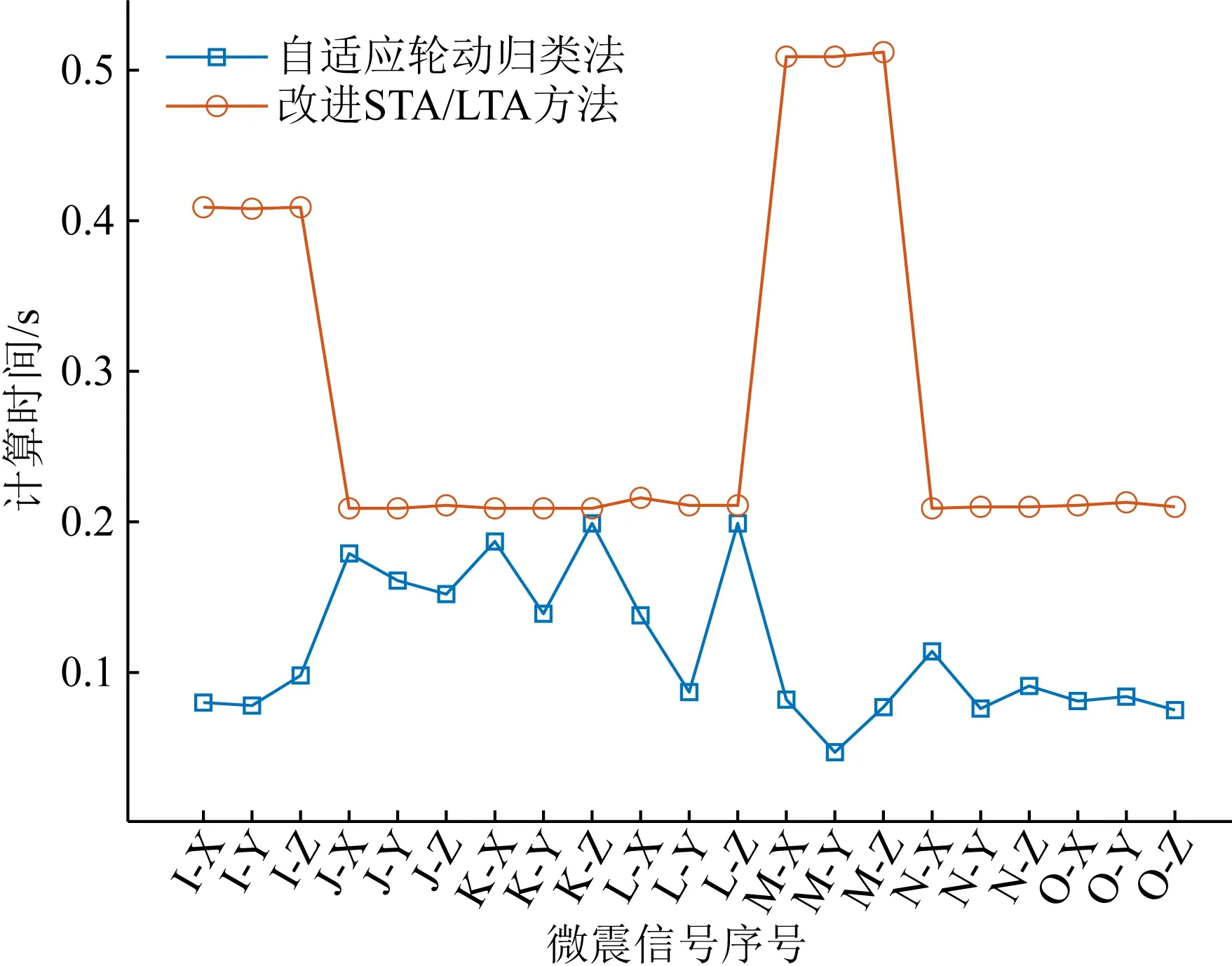
图19 两种方法的计算时间

由图19可知，改进STA/LTA方法的计算时间总体要高于自适应轮动归类法，其计算时间平均值为0.281 s，并且不同震源下的计算时间变化幅度较大，极差为0.303 s.相较改进STA/LTA方法，自适应轮动归类法方法的计算时间较短，计算时间平均值为0.115 s，并且计算时间变化范围也较小，极差为0.152 s.

(3)两种方法识别效果对比

通过对识别结果与计算时间的整理与分析，结果如表6所示.

表6 两种方法震相识别效果对比

由表6可知，相较改进STA/LTA方法，自适应轮动归类法的识别准确率提高了4.8%，识别偏差标准差为前者的34.2%，计算时间平均值为前者的40.9%，计算时间标准差为前者的55.9%，即该方法相较改进STA/LTA方法在震相识别准确率、稳定性以及计算速度、稳定性上均具有一定的优势.

5 结论

本文提出了用于微震信号震相识别的自适应轮动归类法，通过该方法与改进STA/LTA方法对模型试验所得微震信号震相识别效果的对比，分析了自适应轮动归类法的优越性，并在工程实践中获得验证，所得结论如下：

(1)模型试验中不同震源与相同震源下微震信号SNRmss的中位数变化范围分别为0.099～7.818 dB及0.012～3.744 dB，说明发震方式与监测环境对微震信号的有效监测影响较大.

(2)自适应轮动归类法的计算时间、识别偏差与信号长度的相关系数分别为改进STA/LTA方法的86.1%及47.8%，并且计算时间、识别偏差与SNRmss的相关系数更为接近-0.5，说明本文方法可以保证对长度不同信号的识别容错率与稳定性更高，并且能够更好的适应且不过度依赖高SNRmss的信号，保证后期有较大的识别准确率提升空间.

(3)模型试验下，相较改进STA/LTA方法，自适应轮动归类法的识别准确率提高了25.0%，识别偏差标准差为前者的17.4%，计算时间平均值、标准差分别为前者的44.2%、67.4%.实际工程下，本文方法的识别准确率提高了4.8%，识别偏差标准差为前者的34.2%，计算时间平均值、标准差分别为前者的40.9%、55.9%.