瞬变电磁BEDS-FDTD三维正演新算法及稳定性验证

柳尚斌，孙怀凤,3*，李文翰，王震，杨洋,3

1 山东大学岩土与结构工程研究中心，济南 250061 2 山东大学地球电磁探测研究所，济南 250061 3 山东省工业技术研究院先进勘探与透明城市协同创新中心，济南 250061 4 山东大学北京研究院，北京 100086

0 引言

时域有限差分(FDTD)方法最早由Yee(1966)提出，通过在时间和空间上对电场、磁场交替采样，用中心差分对Maxwell的两个旋度方程离散，得到电磁场的显式迭代方程.中心差分具有二阶精度，但需要时间步长Δt严格满足CFL条件才能保证数值稳定性(Wand and Hohmann，1993).严苛的稳定性条件使显式FDTD需要大量的时间迭代步才能模拟晚期瞬变电磁响应，过多的迭代次数不仅会增加模拟时间，同时也会增加晚期的累积误差.Crank-Nicolson时域有限差分法(CN-FDTD)(Fijany et al.，1995；Yang et al.，2006)是一种对任意时间步长都无条件稳定的算法，由于时间步长不再受CFL条件限制，可以采用比ΔtCFL(显式FDTD算法满足CFL条件时的最大时间步长)大的多的时间步长，从而减少时间迭代步数.但由于该算法的电场、磁场采样时刻相同，在差分离散后的求解方程中电、磁场分量相互耦合在一起，每一时间步电磁场的计算都需要求解一个大型稀疏矩阵，不管采用直接法还是迭代法求解，都不可避免地会占用大量内存或时间.因此，相较于原始FDTD算法，CN-FDTD计算效率的提升非常有限.之后，为了提高计算效率，一些学者相继提出了一系列基于CN-FDTD算法的近似策略，例如用于二维的approximate-decoupling策略(Sun and Trueman，2004)和用于三维的direct-splitting(DS)策略(Sun and Trueman，2006)，以及交变方向隐式时域有限差分方法(ADI-FDTD)(Garcia et al.，2002)等.由于这些近似算法不再求解大型稀疏矩阵，而是求解低阶且主对角占优的三对角矩阵，因此可以用快速算法求解(Thomas，1949)，显著的降低内存消耗和计算时间.ADI-FDTD以及CNDS-FDTD算法的无条件稳定性验证在多篇文献(Zheng and Chen，2001；Tan，2008；Jiang et al.，2019)中都有提及.

然而，Yang和Tan(2017)实验发现，ADI-FDTD算法的稳定性并不是完全没有条件，该算法的稳定前提是在均匀时间步长下，当时间步长不均匀时，ADI-FDTD算法不再稳定.本文通过试验发现，CNDS-FDTD算法也存在类似的问题，即在非均匀时间步长下，该算法变的和普通FDTD算法一样，Δt需满足CFL条件，否则，算法很快会发散.而在瞬变电磁三维正演中，时间步的大小并不是均匀的，在早期会采用较小的Δt，使得电磁响应能够反映近地表的电性特征；随着时间的迭代，电磁波中的高频成分迅速衰减，低频逐渐成为主要频段，更大的波长使得没有必要再采用小的Δt，因此会采用更大的Δt来节省模拟时间.根据上面的分析可知，瞬变电磁正演中的时间步长是非均匀的，这意味着如将CNDS-FDTD算法用于瞬变电磁三维正演，由于Δt无法突破CFL限制，正演的效率并不会提高.

Backward Euler(BE)差分格式同样对任意时间步长都无条件稳定，在地球物理数值模拟中有着广泛的应用(Yang et al.，2014；惠哲剑等，2020；齐彦福等，2021).然而，BE差分后的Maxwell方程同样是隐式求解格式，与CN-FDTD方法一样，都面临着求解大型稀疏矩阵的问题.为了提升求解效率，本文将DS近似策略引入到BE差分格式后的FDTD方程中，形成了BEDS-FDTD新方法.DS策略将电磁场分量解耦，并将大型稀疏矩阵降阶和重构为低阶且主对角占优的三对角矩阵，可以采用Thomas算法快速计算.BE方法在时间上是稳定的，但加入DS策略是否会对其稳定性产生影响，以及BEDS-FDTD在有耗介质、非均匀时间步长下的稳定性尚未见报道.借鉴Zheng和Chen(2001)对FDTD类算法无条件稳定性证明的方法，采用von Neumann方法求幅值增长系数，判断算法的稳定性.在实践中发现，在有耗介质、非均匀时间步长下的场幅值增长系数的解析解非常复杂，对于这种未知量过多的符号类函数求解，是一个非常耗时的过程，作者在一台CPU为Intel Core i5-7400的PC机上采用Matlab求解48 h，仍不收敛.因此，本文采用半解析的方式，首先减少未知量个数，将电导率、时间步长给定，然后采用大量随机抽样的方式来计算幅值增长系数，进而对BEDS-FDTD算法的稳定性进行验证.实验结果验证了全新算法BEDS-FDTD在有耗介质、均匀和非均匀时间步长下都是稳定的，这为将BEDS-FDTD算法用于瞬变电磁三维正演提供了理论前提.

1 理论

1.1 PML与普通介质统一控制方程

电磁波的传播本身是一个开域问题，但在数值模拟时，有限的计算资源无法模拟电磁波传播的整个过程，因此需要在模型某处截断，人为添加边界条件.Dirichlet边界条件是最常采用的边界条件，其实质是在模型最外侧添加一层理想电导体(Perfect Electric Conductor，PEC)，电磁波遇到PEC会完全反射.该边界条件施加方式简单，只需在边界网格处强制令电场的切向分量为0即可.然而，如果模型尺寸不够大，由边界反射产生的“伪反射波”会对观测区域的计算结果产生严重影响，而采用过大的模型尺寸又会增加模拟时间.完全匹配层(Perfectly Matched Layer，PML)吸收边界是为了解决电磁场远距离传播所设计的，电磁波在PML介质内传播时会迅速衰减，而且在界面处无反射.通常情况下，PML介质远离发射源所在区域，那么在均匀、各向同性、非磁性媒质中的频率域Maxwell旋度方程(Chew and Weedon，1994)为

(1)

(2)

其中，η代表笛卡尔坐标系下坐标方向，且满足循环移位规律，例如当η=x时，η-1和η+1分别代表z和y方向，ε为介电常数，μ为真空磁导率.S为复数形式的坐标伸缩因子，在CFS-PML介质中，为了改善对低频电磁波的吸收效果，将Sη定义(Roden and Gedney，2000)为

(3)

式中，κη为网格延拓因子，σp η是PML介质中人为添加的电导率，αη是一个大于零的实数.

将方程从频率域转换到时间域，往往通过傅里叶反变换，这不可避免的会引入卷积项，而卷积的计算通常费时费力.为了避免复杂的卷积运算，本文采用双线性变换方法，首先利用关系jω→s将Sη变换到s域，则

(4)

其中，uη=αη/ε0，vη=uη+σp η/(κηε0).

然后采用双线性变换关系s=(2/Δt)·(1-z-1)/(1+z-1)将(4)式变换到Z域：

(5)

其中，

将(5)式代入到方程(1)和(2)中，并将两个方程等号左侧的jω用其Z域的表达式(1-z-1)/Δt替换，可得到Maxwell旋度方程在Z域下的形式

(6)

(7)

式中，系数w、φ和θ下标中的e代表的是求解电场，h代表的是求解磁场，但计算公式是相同的.将方程(6)和(7)化简：

(8)

(9)

其中，a0=ε/(ε+σΔt)，a1=Δt/(ε+σΔt)，b=Δt/μ.如果令

(10)

将式(10)展开并化简，可得到Ψe(η,η+1)的计算公式：

(11)

同理，如果令

(12)

可得到Ψe(η,η-1)的计算公式：

(13)

将式(10)和(12)代入到方程(8)中，并考虑式(11)和(13)，整理得

Eη=a0z-1Eη+(Ψe(η,η+1)-θe(η+1)z-1Ψe(η,η+1))-(Ψe(η,η-1)-θe(η-1)z-1Ψe(η,η-1))

(14)

如果令reη=φeη-θeη，并将方程(14)在n+1时刻差分离散，同时考虑到Z变换的时移特性，经整理，得到时域方程为

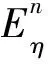
(15)

其中，D代表一阶中心差分算子.

(16)

(17)

同理，方程(9)经过相似的变换，可得到下式

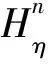
(18)

其中，

(19)

(20)

经过上述的处理过程，方程(15)和(18)在时间上为BE差分格式，下面进行简单证明.将时间域Maxwell旋度方程中场对时间的一阶导数用BE差分近似，可得

(21)

(22)

将上面两个方程(21)和(22)写成分量形式，并化简：

(23)

(24)

其中，η、a0、a1和b与上文中的定义一致.

分析方程(15)、(18)，当w和Ψ分别取值1和0后，即将PML介质内的迭代方程退化到普通介质内的迭代格式时，它们与方程(23)、(24)完全一致.因此，我们通过选择合适的变换关系得到的方程(15)和(18)是在时间上满足BE差分格式的电、磁场方程.

1.2 引入DS策略的近似算法

若要对方程组(15)和(18)求解，可将(18)代入(15)中，使得新方程的左侧不再包含n+1时刻的H，化简后，可得

(25)

其中，D2代表二阶中心差分算子.

由方程(25)可以看到，等号的左侧是n+1时刻的场值(待求量)，等号的右侧是n时刻的场值(已知量)，可通过求解线性方程组来计算待求场值.但在等号左侧，由于电场的不同方向、不同空间位置的分量相互耦合在一起，使得需要处理的系数矩阵是一个大型稀疏矩阵，这种类型的矩阵无论是采用直接法还是迭代法求解，都不可避免地会占用大量内存和时间.为了提升求解效率，本文将DS策略引入到求解方程中，将方程(15)和(18)写成下列矩阵的形式：

(26)

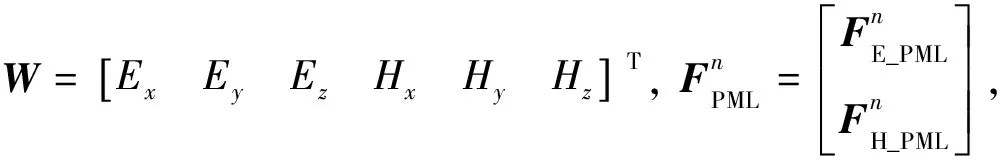
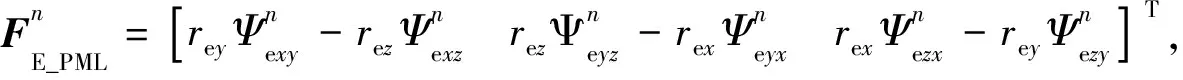
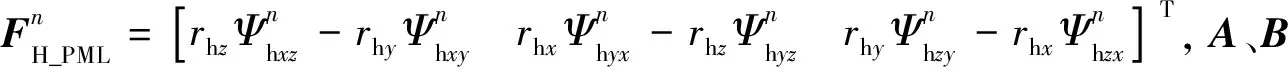
在方程(26)的左侧加入高阶误差项AB(Wn+1-Wn)，整理后得

注意到方程(27)等号左侧可做因式分解，因此求解过程可分为以下两个子步骤：

(28)

(I6-B)Wn+1=W*-BWn，

(29)

其中，场值的上标“*”代表非真实的采样时刻，是为了方便计算而引入的中间过程.将算子矩阵A、B和C代入方程(28)和(29)中并化简，可得

(30)

(31)

En+1=a1MTHn+1+E*-a1MTHn，

(32)

Hn+1=bMEn+1+H*-bMEn.

(33)

通过一系列变换可使得方程(30)、(32)和(33)中等号的右侧不包含H*和Hn+1，然后将矩阵M代入并整理，得

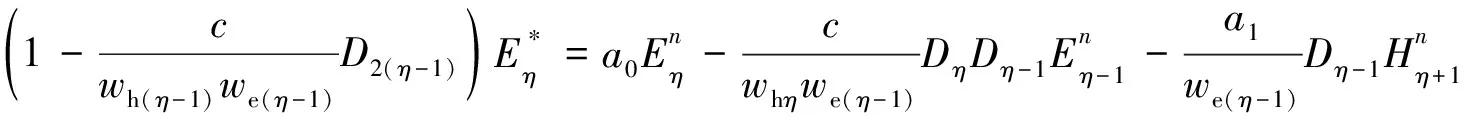
(34)

(35)

(36)

式中，c=a1b.

方程(34)—(36)即为BEDS-FDTD算法在PML介质中的控制方程，其求解过程为：首先通过方程(34)计算E*，再通过方程(35)计算n+1时刻的电场，最后由方程(36)显式迭代计算n+1时刻的磁场.需要说明的是，这里计算的磁场不是真实的物理场，而是一个中间量，若要得到真实的磁场，需将电场值代入式(18)中求解.BEDS-FDTD算法在普通介质中的控制方程和在PML介质中的控制方程，均可写成(34)—(36)的形式，当w和Ψ分别取值1和0后，该控制方程就退化到普通介质内的格式.

1.3 系数矩阵快速求解

以方程(34)为例，当η=x时，通过z方向的坐标逐行变化(x和y坐标不变)，方程可写为

(37)

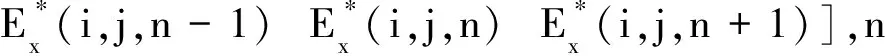
(38)

(39)

(40)

其中，2≤k≤n.那么系数矩阵P1为

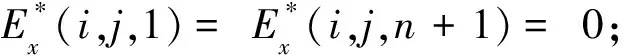
矩阵P是满秩矩阵，且只有三个主对角上有非零元素，考虑到α、β和γ的表达式满足不等式条件：|β2|>|γ2|>0，|βk|≥|αk|+|γk|，αk、γk≠0，k=3,4,…,n-1；|βn|>|αn|>0.因此，矩阵P是主对角占优的三对角矩阵，可以采用Thomas算法快速求解.

2 稳定性验证

当在瞬变电磁正演中对复杂地形模拟时，地空边界采用向上延拓不再适用，此时不可避免地需要将空气层引入到计算内，理想的空气是无耗介质(σ=0 S·m-1).但在实际的算法设计中，不会让空气的电导率真正的为0，而是给一个足够小的值(例如，σ=10-6S·m-1)，此时，空气由无耗介质转为有耗介质；除了空气之外，大地本身同样为有耗介质.当算法用于瞬变电磁三维正演时，需要考虑这种使用场景下的特殊条件，包括时间步长非均匀(参考引言中的内容)、介质有耗，所以下文主要讨论这种特殊情况下算法的数值稳定性.

本文采用von Neumann方法求幅值增长因子来判断算法的数值稳定性(陈娟等，2016)，如果计算的场幅值增长系数均小于或等于1，那么说明该算法是稳定的；否则，说明该算法是不稳定的.由于在瞬变电磁正演中的时间步长不均匀，只考虑从n时刻到n+1时刻的场值增长情况并不能反映算法在非均匀时间步长下的稳定性，需要增大观测时间，考虑从n时刻到n+2时刻的场值增长情况.BEDS-FDTD算法的最根本求解方程为方程(27)(之后的一系列数学变换都是基于该方程)，为了简化计算，下面仅考虑普通介质中的方程

(41)

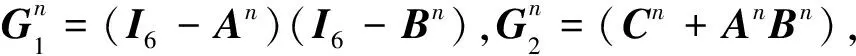
在线性、各向同性介质中传播的平面波方程为

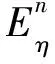
(42)

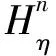
(43)

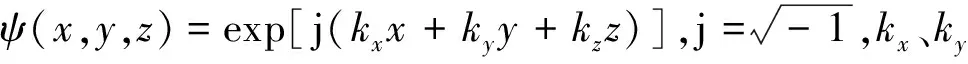
当η=x时，将函数ψ对空间的导数进行中心差分离散：

(44)

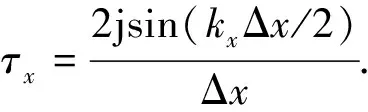
同理，当η=y,z时，也有类似的表达式：

Dyψ(x,y,z)=τyψ(x,y,z)，

(45)

Dzψ(x,y,z)=τzψ(x,y,z)，

(46)

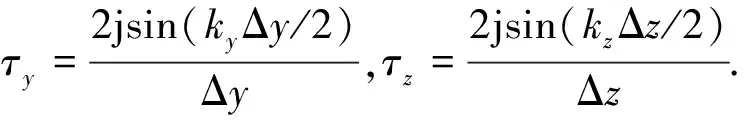
将式子(42)—(46)代入方程(41)中，得到BEDS-FDTD从n时刻到n+1时刻的场值计算公式

(47)

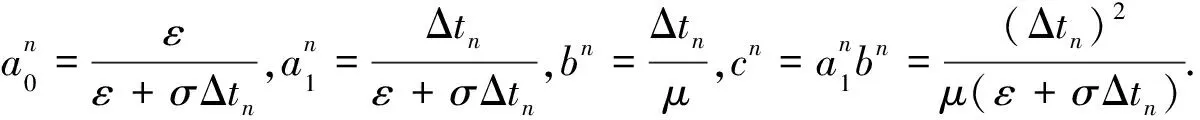
同理，BEDS-FDTD算法从n+1时刻到n+2时刻的场值计算公式可写做

(48)

式中，

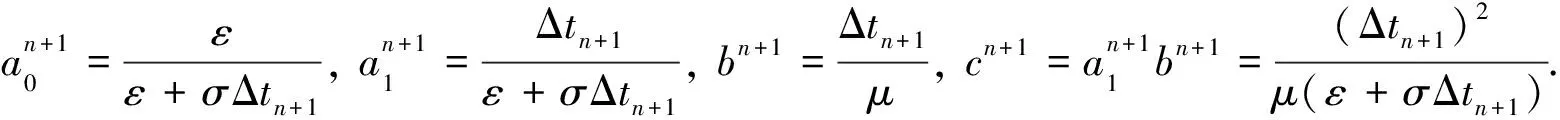
综合考虑公式(47)和(48)，从而得到BEDS-FDTD算法从n时刻到n+2时刻的迭代公式：

(49)

式中，右上角的“-1”代表矩阵求逆运算.考虑平面波方程(42)和(43)，可以得到Wn+2=ξ2Wn；那么，方程(49)经整理、化简为

(50)

若方程(50)具有非零解，系数矩阵的行列式必须为零，所以：

(51)

通过求解式(51)可获得幅值增长系数ξ的解析解，然而，由于式(51)中的未知量过多，很难求得ξ解析解的表达式.本文采用半解析的方式，用大量随机抽样的方式计算ξ.首先减少未知量的个数，令空间网格的尺寸为10 m，空气电导率σ=10-6S·m-1.若Δtn=αΔtCFL，Δtn+1=βΔtCFL，那么可记作CFLN(n,n+2)=(α,β)；在Matlab R2020上对kx、ky和kz各随机抽样取值1000次，将计算的|ξ|绘制在复平面的上半平面上.为了方便对比，将采用同样方法计算的CN-FDTD和CNDS-FDTD算法的结果同样绘制在图中.图1a、1b展示了非均匀时间步长下的结果，在图1a中非均匀时间步长为CFLN(n,n+2)=(2,8)，从图1a可以看到，原始CN-FDTD算法的|ξ|位于单位圆的圆周上，这意味着CN-FDTD算法是稳定的，但近似算法CNDS-FDTD却在某些波数时失去了稳定性.考虑到相邻Δt变化的过于剧烈，在图1b中展示了当CFLN(n,n+2)=(2,3)时的结果，图1b的结果与图1a中的现象是一致的，CNDS-FDTD算法同样发散了.作为对比，本文提出的全新算法BEDS-FDTD在CFLN(n,n+2)=(2,8)和CFLN(n,n+2)=(2,3)时的|ξ|都位于单位圆内，这说明BEDS-FDTD在不均匀时间步长下是稳定的.图1c和1d中展示了均匀时间步长下三种算法的结果，可以看到，三种算法在均匀时间步长下都是稳定的.

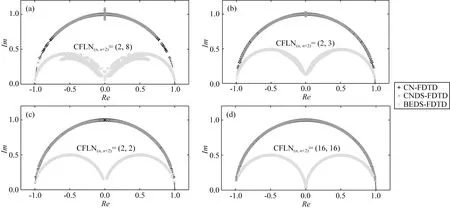
图1 从n时刻到n+2时刻的场值增长系数ξ

从上面的分析可以看出，尽管原始CN-FDTD算法在均匀和非均匀时间步长下都是稳定的，但近似后的CNDS-FDTD算法却只能在均匀时间步长下维持稳定，在非均匀时间步长下不再稳定.而本文提出的新算法BEDS-FDTD，不管是在均匀时间步长还是非均匀时间步长下均能保持数值稳定.上面的实验结果为新算法BEDS-FDTD应用到瞬变电磁三维正演中提供了理论前提.

3 模型试验

3.1 BEDS-FDTD算法计算效率与精度测试

为了检验新算法BEDS-FDTD用于瞬变电磁三维正演的适用性和效率，本文将其用于典型层状模型的模拟中，选择的第一个测试模型为H型模型，模型参数细节如表1所示.空气的电导率为σ=10-6S·m-1，大地与空气的相对介电常数均为εr=7.8.110 m×110 m的矩形回线敷设在空气与大地之间作为发射源，电流为1 A，发射波形采用梯形波(孙怀凤等，2013)，波形1的具体参数如图2所示，除此之外，本文还设计了波形2，与波形1的区别是Turn-off时间由10-6s改为10-7s.模型(包括PML介质区域)采用均匀网格剖分，网格尺寸采用两种方案，策略1是网格在x、y和z方向上的尺寸为22 m×22 m×20 m；策略2是网格在x、y和z方向上的尺寸为10 m×10 m×10 m.PML介质的参数按照下式选取：

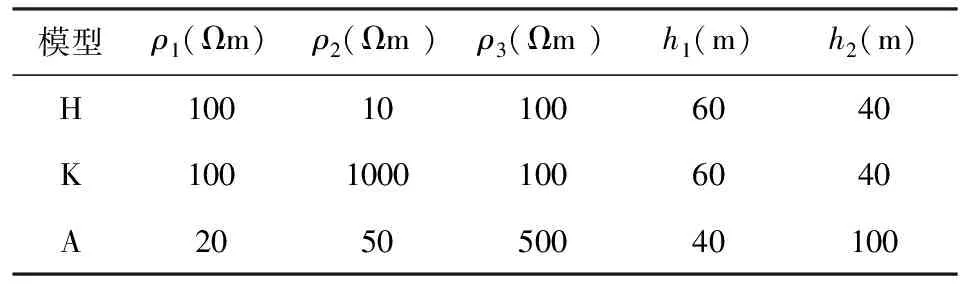
表1 模型参数

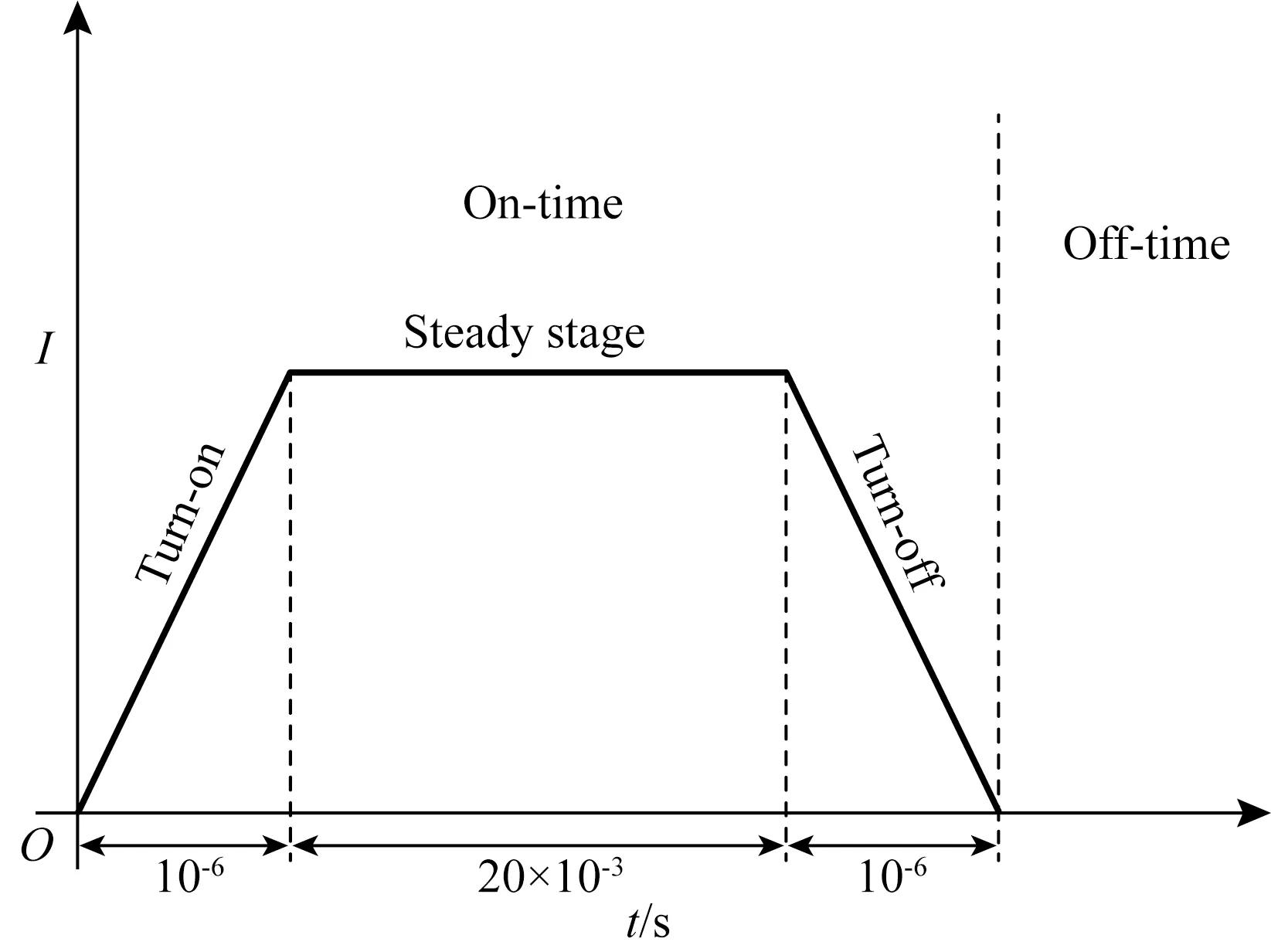
图2 激励波形示意图

(52)

(53)

(54)

其中，d是PML介质的厚度；x是PML介质中的某点距离PML与正常介质的分界面的距离，m和ma为多项式的阶数，影响着参数的变化速度，通常情况下ma=1，m=3；本文经过大量的模拟测试后发现，在参数σmax=1.0×10-2S·m-1，αmax=1.0×10-4S·m-1和κmax=1.0时，CFS-PML边界能取得较好的吸收效果.

BEDS-FDTD算法求解过程中，最耗时的部分为时间步迭代过程，其中包含了大量的多重循环，这种结构非常适合并行加速.本文算法的代码基于GPU并行计算的OpenACC框架编写，实验中的GPU采用专门用于高性能计算(High performance computing，HPC)的专业卡Tesla A100.由于BEDS-FDTD算法使用了吸收边界，通常不需要考虑太多的网格数目，但更多的网格可以模拟更加精细的模型，因此本次实验将网格数量作为变量测试算法的效率，所有模型的网格数均包括外部10层的CFS-PML介质，模型剖分采用策略1.图3给出了BEDS-FDTD算法和常规FDTD算法在不同网格数量时的计算效率对比.可以看到BEDS-FDTD算法在模拟网格数为50×50×50(图3中计作503)的模型(计算域是30×30×30)时，整个计算过程共需要16000个迭代时间步，用时仅10 s，而即使网格数增加到200×200×200(图3中计作2003)，用时也仅224 s，计算效率非常高.作为对比，同样采用了CFS-PML边界以及GPU并行的FDTD算法的整个计算过程共需要233000个时间迭代步，需要注意的是，该FDTD算法已经考虑了虚拟介电常数(孙怀凤等，2013)，即在确保传导电流占据主导时，时间步长相较于普通FDTD已经有了很大的增长.但由于迭代时间步数仍远超BEDS-FDTD，FDTD在计算不同尺寸的模型时，平均用时要比BEDS-FDTD多9倍左右.

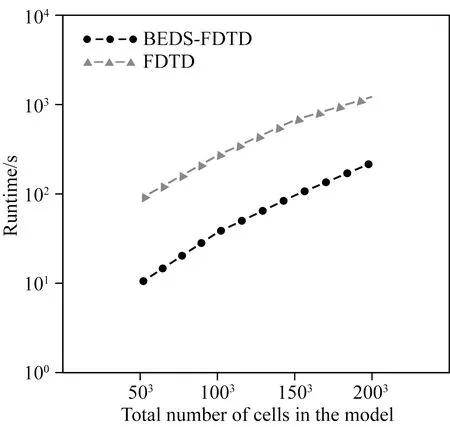
图3 BEDS-FDTD和FDTD算法在计算不同数量网格时的效率

为了验证BEDS-FDTD算法的精度，我们将采用不同波形、不同网格剖分策略的H模型(网格数都为50×50×50，计算域为30×30×30)的数值解与一维数字滤波解(李貅，2002)做了对比，观测时间为电流关断后10-5～10-2s，计算结果如图4所示.图4a中是数值解与数字滤波解的对比，图4b为相对误差曲线.可以看到，当BEDS-FDTD算法采用网格剖分策略1时，采用波形2的解比采用波形1的解在早期精度更高；而在晚期，两者的精度是一致的，这和文献(Zeng et al.，2019)中的结论一致，即更短的关断时间会使得模拟结果的早期精度更高；而采用网格剖分策略2和波形2的BEDS-FDTD的解精度最高，在观测时间内，与数字滤波解的相对误差都在5%以下，满足模拟计算要求.在图4中还绘制了同样采用网格剖分策略2和波形2的FDTD的解，可以看出，整体的误差和BEDS-FDTD算法的误差基本上处在同一水平，但值的关注的是，晚期(电流关断3 ms之后)FDTD的误差有继续扩大的趋势，而且其晚期的误差值要大于BEDS-FDTD的误差.本次实验表明，不仅电流的关断时间会对算法的早期精度产生明显的影响，网格的大小同样会对计算结果的早期精度产生显著影响.而且，实验结果也证明了本文针对全新算法BEDS-FDTD提出的CFS-PML边界非常有效，在较小的模型尺度下(采用网格剖分策略2时，包括PML介质的整个模型尺寸为500 m×500 m×500 m)也能获得精度非常高的结果.

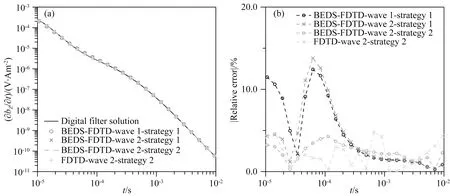
图4 H型模型的BEDS-FDTD数值解与一维数字滤波解的对比

为了进一步验证计算精度，本文还将BEDS-FDTD算法用于模拟K型层状模型，参数如表1所示，模型(包括PML介质)采用第二种剖分策略(网格大小为10 m)，网格数量为50×50×50，其中PML介质在各个方向上占据10个网格，因此，计算域大小为30×30×30.发射源的参数与H型模型的一致，发射电流波形采用波形2，计算结果展示在图5中.从图中可以看出，除了早期外，数值解与一维数字滤波解均吻合的较好，而早期差异较大的原因是由于BEDS-FDTD发射波形2虽然对阶跃波进行了模拟，但实际上只是修改后的梯形波，关断效应导致了与采用阶跃波响应的数字滤波解在早期差异较大，而随着关断效应的逐渐减弱，在大部分观测时间内，二者的相对误差都不超过5%.

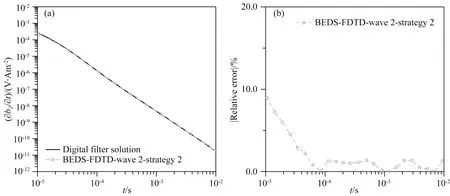
图5 K型层状模型的BEDS-FDTD数值解与一维线性数字滤波解的对比

在上面的精度验证模型中的激励源都是回线源，下面的算例中用A型层状模型验证算法在电性源激励下的计算精度.模型的具体参数如表1所示，采用网格剖分策略2剖分，模型在x、y和z方向上的网格数为50×50×50，各个方向最外面的10层为PML介质(PML介质的参数与上面的模型一致)，因此，计算域的网格数目为30×30×30.发射源为110 m长的接地线源，发射电流为1 A，发射波形采用波形2.接收点距离线源的中心110 m，图6a绘制了接收点处的感应电动势随时间的变化曲线，图6b展示了数值解与数字滤波解的相对误差.可以看到，模拟结果与数字滤波解吻合的较好，误差在大部分时间内均小于5%，仅在极早期大于5%，具体原因在K型模型中进行了详细说明，这里不再赘述.

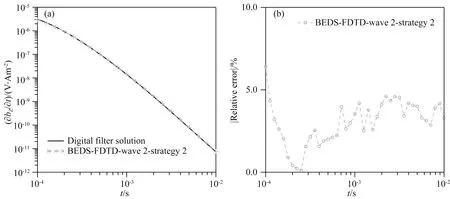
图6 A型层状模型的BEDS-FDTD数值解与一维线性数字滤波解的对比

3.2 复杂模型实验

为了测试BEDS-FDTD算法的适用性，本文将其用于复杂三维模型的计算，模型的具体细节如图7所示.空气的电导率为σ=10-6S·m-1，大地与空气的相对介电常数均为εr=7.8.大地表面是一厚50 m，电导率为0.1 S·m-1的覆层，薄层下面存在着一个形状非常复杂的三维低阻体(在z方向上呈阶梯状分布)，电导率为1 S·m-1，该低阻体将大地分成电导率为0.01 S·m-1和0.003333 S·m-1的两部分.100 m长的导线敷设在如图7所示位置，发射电流为1 A，发射波形采用波形2.PML介质的参数与层状模型选取的一致.整个模型在x、y和z方向上为900 m×2050 m×1200 m，采用均匀网格剖分，网格在x、y和z方向的尺寸为10 m×12.5 m×10 m.计算域为70Δx×144Δy×100Δz，最外侧包裹了10层的PML介质.

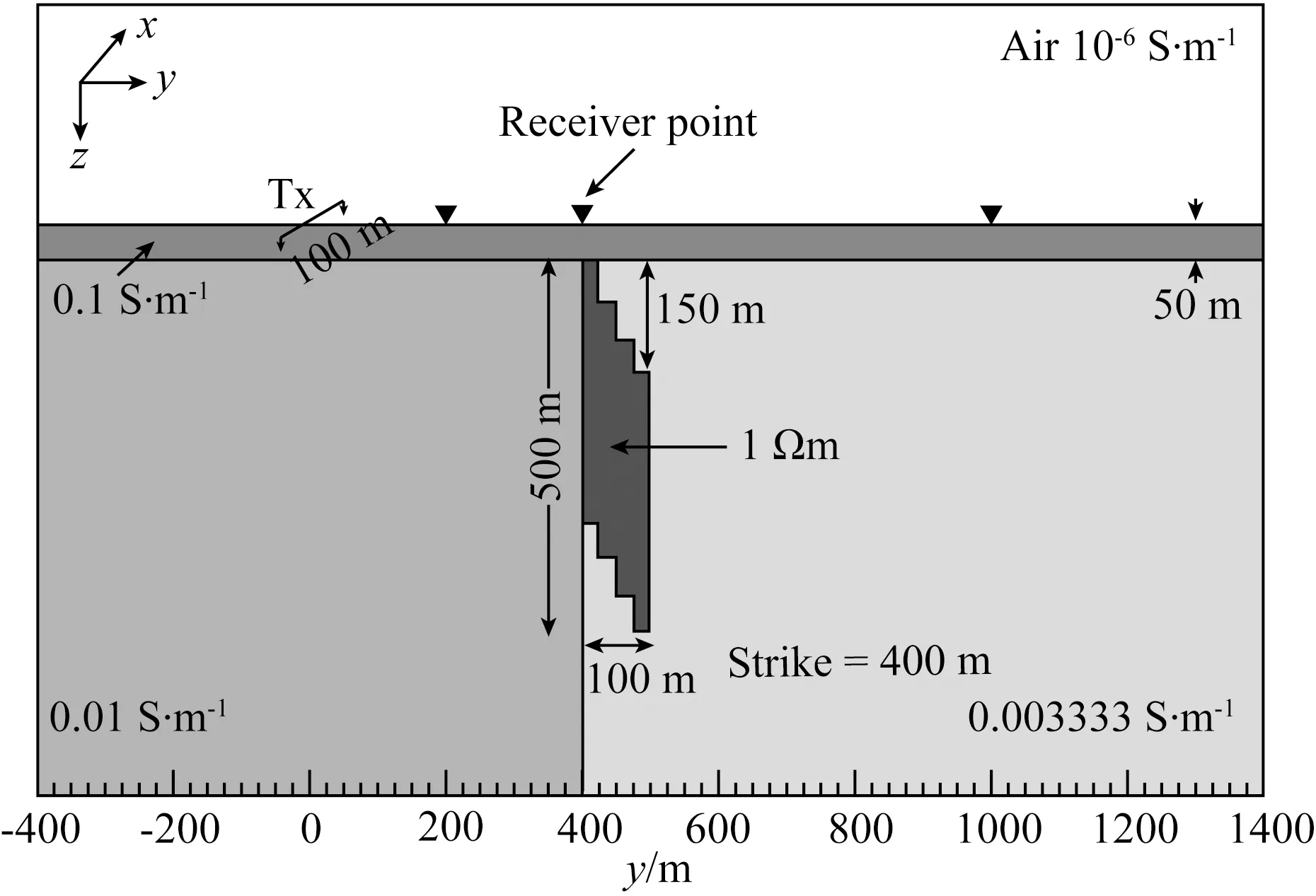
图7 复杂三维模型示意图

坐标的中心位于发射线源的中心，图8绘制了三个观测点处的感应电动势的结果.图中曲线突变的地方为数据从正值转为负值，从图中可以看到，BEDS-FDTD的结果与FDTD(Commer et al.，2004)和MFVTD(Liu et al.，2019)的结果一致性非常好，在具体细节上，本文提出的BEDS-FDTD的结果与FDTD的结果吻合的程度更高，在整个观测时间内，基本看不出明显的偏差.

图8 复杂模型的计算结果

4 结论

本文提出了瞬变电磁三维正演新算法BEDS-FDTD，该算法在有耗介质、均匀和非均匀时间步长下均能维持无条件稳定性，而且其时间步长不再受CFL稳定性条件限制，可有效减少迭代次数.DS策略的引入将大型稀疏矩阵转变为一系列低阶、主对角占优的三对角矩阵，可快速求解.实验发现，采用GPU并行后，用Tesla A100模拟50×50×50规模的模型，精度能满足计算要求的情况下仅用时10 s.即使模型规模扩大到200×200×200，用时也不超过4 min.之后，将新算法BEDS-FDTD用于不同复杂程度的模型计算中，计算结果验证了该算法具有较高的精度.模型实验证明了BEDS-FDTD算法是稳定、高效的，可为瞬变电磁三维快速反演提供正演基础.

致谢本文在孙怀凤等(2013)开发的TEM3DFDTD程序基础上完成.作者在研究过程中就时间步长的选择与算法精度的问题与长安大学的齐彦福老师进行了深入讨论；审稿专家对本文写作的提高提出了很多建设性的意见，在此一并表示感谢.