背景噪声互相关函数多尺度成像研究
2023-02-11黎昌成陈晓非2
黎昌成,陈晓非2,,3*
1 南方科技大学地球与空间科学系,广东深圳 518055 2 深圳市深远海油气勘探技术重点实验室(南方科技大学), 广东深圳 518055 3 南方海洋科学与工程广东省实验室(广州),广州 511458
0 引言
背景噪声成像方法已被广泛用于不同尺度地下介质结构成像中(Shapiro et al.,2005; Yao et al.,2006;Xia et al.,1999,2003;Harmon et al.,2007;Shen and Ritzwoller,2016;Pan et al.,2019).通常我们会对背景噪声进行处理,然后获得有效信息:如走时(Poli et al., 2012a; Mroczek and Tilmann, 2021),振幅(Knapmeyer-Endrun et al., 2016,2017),波形(Tromp et al., 2010; Sager et al., 2018a, 2018b),频散曲线(Shapiro et al., 2005; Wang et al.,2019; Xi et al., 2021)等.传统基于频散曲线成像方法,通常从两个台站间的互相关函数中提取基阶频散曲线来进行直接计算(Shapiro et al., 2005;Yao et al.,2006,2008).近年来,为了减少反演多解性,从互相关函数中提取高阶频散曲线来反演地下介质结构的方法受到越来越多的关注(Xia et al.,2003; Ikeda et al.,2013; Wang et al.,2019; Pan et al.,2019; Wu et al.,2020).但频散曲线方法主要基于层状假设,推广到二维三维复杂介质成像有降低空间分辨率风险.因此,近年来直接利用互相关函数来进行成像的方法也得到了发展,基于背景噪声互相关函数的反演方法已在全球尺度结构成像中证实可以提高反演模型分辨率(Tromp et al., 2010; Sager et al., 2019),但是该方法依赖于噪声源的全球分布,导致无法推广到局部区域尺度地下介质结构成像上(Sager et al.,2019).因此,本文提出了不依赖于噪声源的互相关函数成像方法.另一方面,不同多尺度类反演方法和策略被广泛应用于不同地震成像领域(Gorbatov and Kennett,2003; Lebedev and van der Hilst,2008;Tian et al.,2009;Fishwick et al., 2005; Zhou et al., 2006; Nettles and Dziewoński,2008;Fichtner et al.,2013; 徐义贤和王家映,1998;潘纪顺等,2009; 张文生等,2015;孙楠等,2021);为了减小计算量增加反演稳定性,Bunks等(1995)基于模型重采样方法,对大尺度模型进行了反演.在地震勘探领域,多尺度反演主要集中于用低频反演得到大尺度初始模型,然后直接加入高频信号,恢复更加精确的结构(Virieux and Operto,2009;Fu et al.,2020;朱宝衡和谢春丽,2021),但这种策略受网格大小限制并不能从模型尺度上对分辨率进行提高.虽然可以通过划分更加精细的网格来提高分辨率,但精细网格对计算量、反演稳定性等方面均会有影响.因此,需要提出新的多尺度反演方法权衡反演深度、稳定性、以及计算量.在背景噪声成像中,实际数据采集,信号处理(从背景噪声数据中提取有效信号),正演,反演是其重要组成部分.因此,本文将系统的从互相关函数处理以及正反演三个方面对互相关函数多尺度成像方法进行研究,并提出尺度随频率变化的多尺度反演方法和策略,为获得更深大尺度和浅部精细结构提供新的方法和策略.
1 理论方法
在背景噪声成像理论方法中,数据处理、正反演方法均是成像的重要组成部分.
对于背景噪声信号处理,如何获得稳定的噪声互相关数据,并且衡量实际数据误差的不确定性对于反演十分重要.前人基于各种有效方法从背景噪声中获得了稳定的互相关函数(Benson et al.,2007;Weaver and Yoritomo 2018;Li et al.,2020;Xie et al.,2020;Yang et al.,2020).为了确定互相关函数中不同时刻有效信号权重,本文采用如下方法对噪声互相关进行处理(Aster et al.,2012).
对于不同时间段获得的互相关函数将其写成矩阵形式:
d=[d1,d2,d3,…,dn]T,
(1)
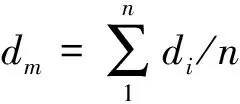
X=[d1-dm,d2-dm,d3-dm,…,dn-dm]T,
(2)
协方差矩阵为
C=diag(XTX),
(3)
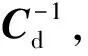
任意选取若干段实际噪声数据,对不同时间段背景噪声数据处理得到的互相关函数,对其求平均可得反演所需数据和数据协方差矩阵对角线元素.结果分别如图1和图2所示,为避免不必要噪声误差,数据处理时,对确定噪声误差段添加了零权重因子.
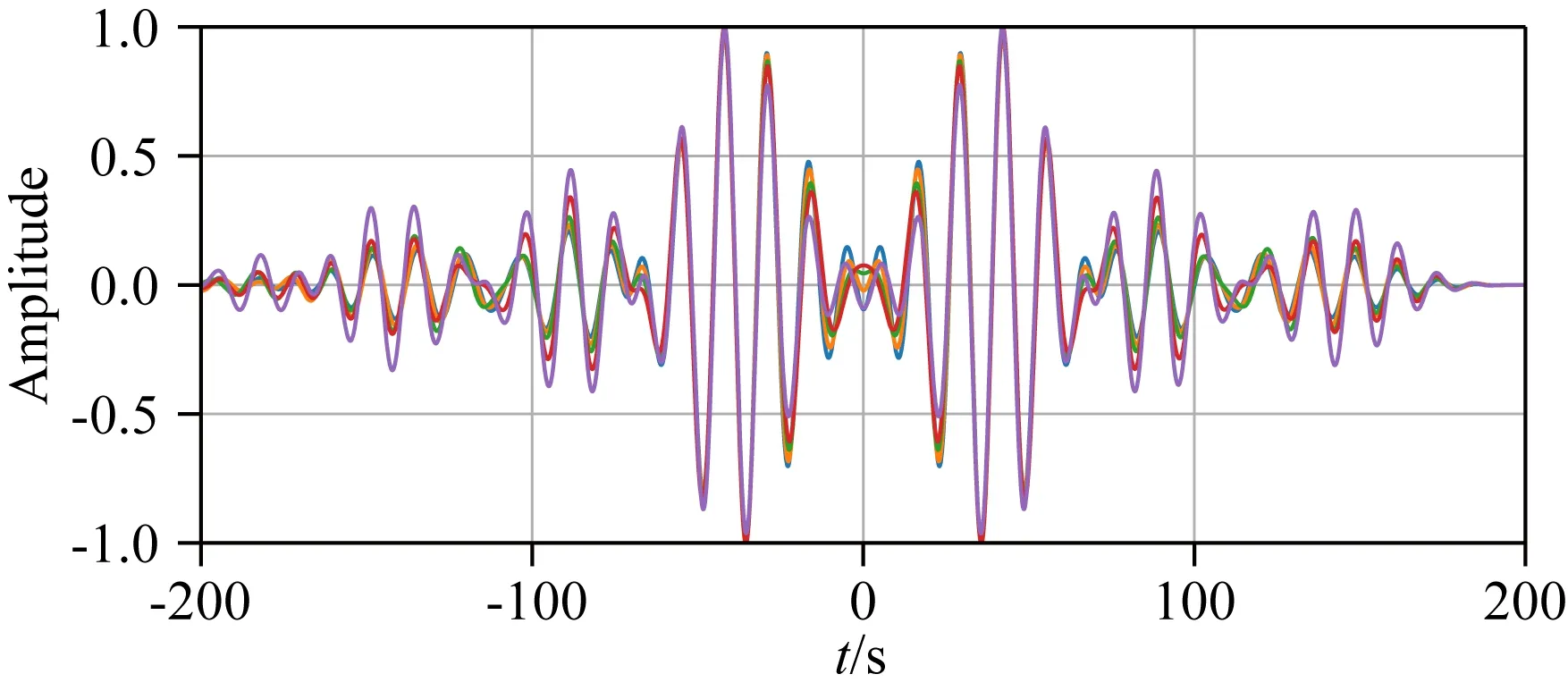
图1 不同时间背景噪声合成的互相关函数实部信息
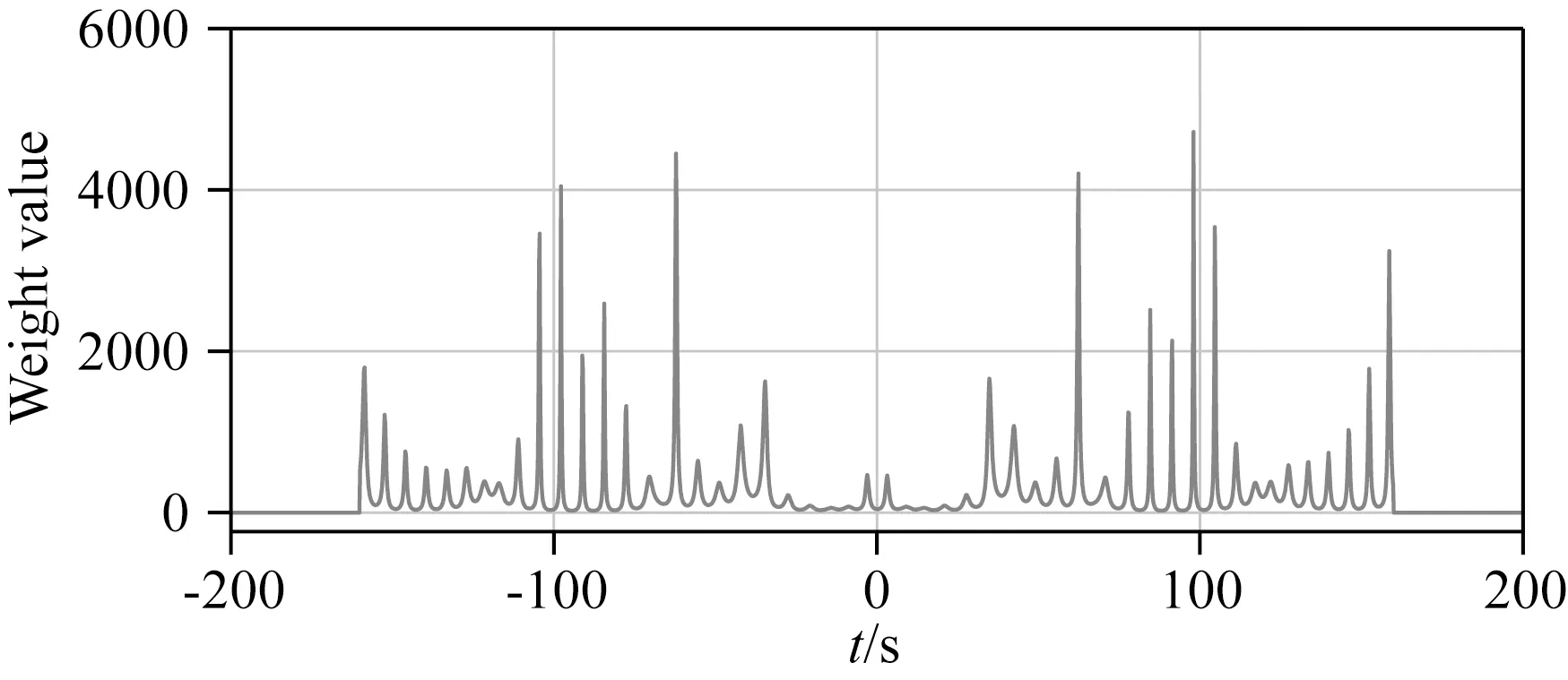
图2 由不同时间互相关函数所求得的协方差矩阵对角线元素
除背景噪声信号处理外,本文方法成立的前提条件之一便是正演方法的发展与成熟.因此,首先建立地下模型参数与噪声互相关函数之间的关系式,然后求解该方程.前人给出了背景噪声互相关函数与格林函数之间的关系(Sánchez-Sesma and Campillo,2006; Sato et al., 2012; Haney et al., 2012; Haney and Nakahara,2014):
(4)
互相关函数实部与格林函数虚部成正比,其中A在单一频率下为常数,可以通过归一化的方法消除影响.C为互相关系数,i,j从1到3表示不同Z,R,T分量,G为格林函数,其为单位点力源在一个台站激发,然后在另一个台站接收到的波形.r为两台站之间的间距,z=0表示震源和接收点都位于地表.w表示角频率.Im表示虚部.上述公式正确性,已被广泛验证(Wang et al., 2019;Li and Chen,2020;Hu et al., 2020),当然该公式从频率域变换到时间域具有一定近似性,通常选择较窄频段范围,使频率近似为常数.
对于一个层状弹性半空间模型,基于点力源格林函数垂直分量可以用公式(5)计算(Chen, 1993; Wang et al., 2019; Li et al., 2020):
(5)
其中:J0表示零阶第一类贝塞尔函数,k表示波数,r为两台站间距,dk表示对波数积分,g表示核函数,其是基于各向同性层状假设,由广义反射透射系数计算得到,其虚部主要表示频散曲线,其包含地下介质物性参数信息,Chen(1993)给出了具体表达公式.将公式(5)代入到公式(4)可得
(6)
求解式(6)便可由地下模型参数得到互相关函数实部,然后利用互相关函数实部信息反演地下介质结构.为了确定合适的反演策略和方法,首先建立相应的目标函数,然后进行敏感性分析.从互相关函数中的核函数g的计算可知,影响互相关函数的因素较多,主要有层厚和层位深度,地下介质物性参数(主要指纵横波速度以及密度),震源与接收点距离,频率,以及滤波器种类等.对于资源探测,地下介质物性参数及其所在位置较为重要,因此本研究主要考虑物性参数和层厚敏感性.
反演目标函数为
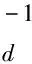
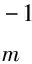
(7)
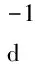
接着考虑目标函数对模型参数导数为
(8)
其中,
(9)
表示目标函数梯度.
对于模型m0,敏感性计算公式为
(10)
其中,
d0=G(m0),
(11)
表示基于模型m0正演计算得到的互相关函数,协方差矩阵应由实际数据计算得到,在理论分析中,选择单位矩阵.
接着基于一个递增模型分析互相关函数对模型参数的敏感性,为后面反演地下介质结构提供理论基础.单一频率敏感性计算频带宽度为0.02 Hz.计算归一化结果如图3b所示.
图3a为横波模型参数,纵波与密度由经验公式给出(Shen and Ritzwoller,2016;Wu et al.,2020).图3b显示的是0.05~0.3 Hz频段范围的互相关函数对模型参数m(依次为纵波速度,密度,横波速度)敏感性归一化结果,从图3b中可知,互相关函数主要对横波速度敏感,对纵波及密度敏感性较低.当同时反演三个参数时,密度与纵波速度容易陷入局部极值,因此,在反演时仅反演横波速度,而用经验关系给出大致的纵波速度与密度值(Pan et al.,2019;Wu et al.,2020).具体经验公式为(Brocher,2005;Shen and Ritzwoller,2016):
(12)
(13)
本文方法是根据各向同性层状假设,而实际互相关函数的提取并无这一假设,当频率变高时,半空间层状介质假设已不能满足实际波场传播特征,此时需要用更加精细的方法如有限差分等方法对地下介质进行剖分.图3c和3d敏感性分析表明,高频对浅部小尺度结构较为敏感,而低频主要对深度大尺度模型较为敏感,当然敏感性具体与模型有关.影响敏感性因素较多,当层厚较小,反演层数和参数较多时,会使得反演结果易收敛到局部极值,因此,对于同一深度的模型可采取增大模型厚度的方法来进行反演.本文所要介绍的多尺度反演方法是对同一个深度的模型,在不同反演阶段进行不同层厚的划分,然后用不同频率的数据进行反演,为反演不同尺度结构和深度的模型以及权衡计算效率提供方法.
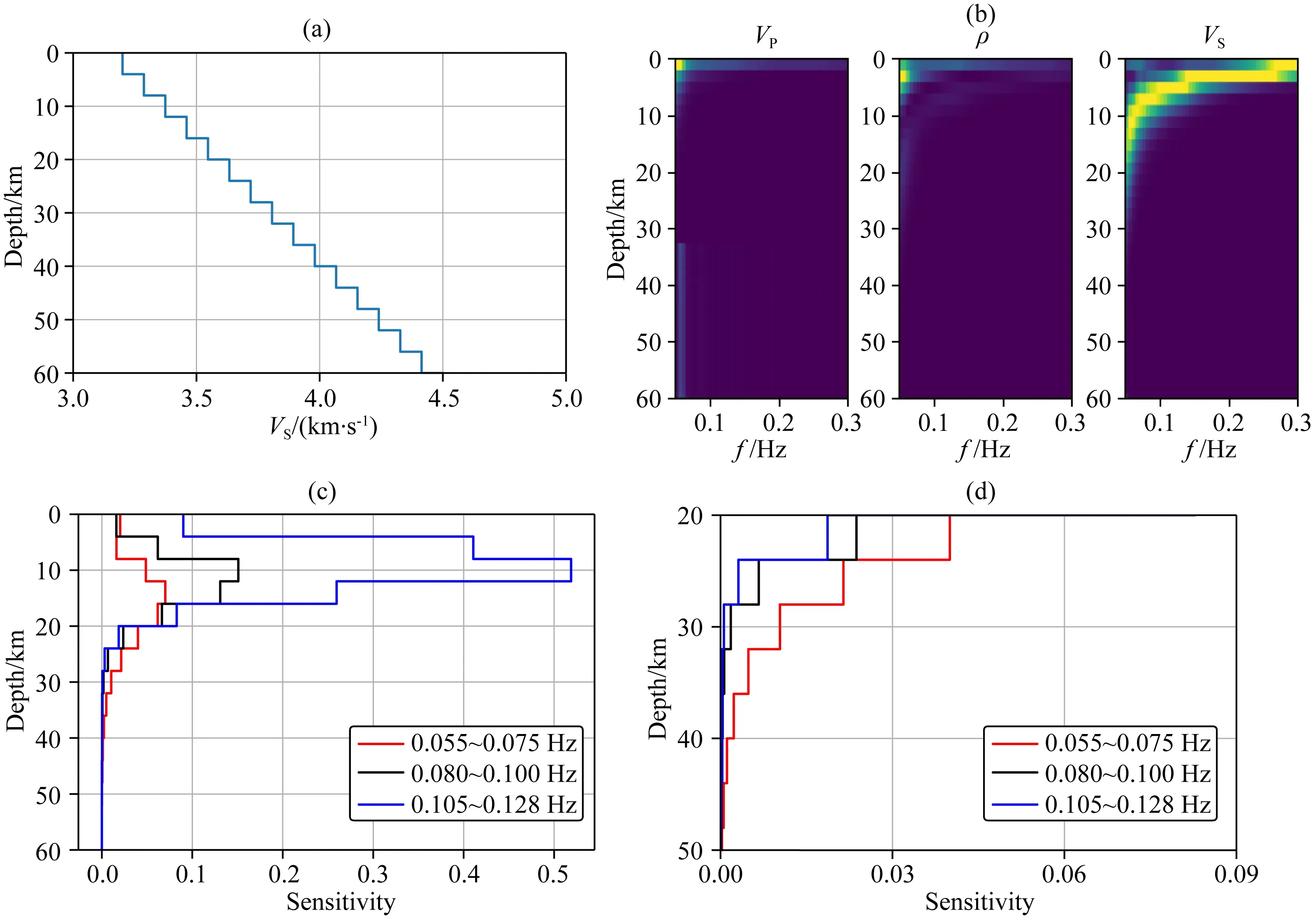
图3 (a)物性参数模型;(b)不同物性参数敏感性结果;(c)不同频段数据敏感性结果;(d)不同频段数据在深部敏感性结果
2 数值试验
2.1 合成数据模型测试
为了验证上述理论,首先进行理论合成数据试验.设计图4a所示背景噪声模拟和采集系统,采集背景噪声,并合成互相关函数进行反演,初步验证互相关函数反演可行性.图4a噪声合成模型中两台站分别位于(50 km,0 km)和(-50 km,0 km)处,点力噪声源均匀分布于60~260 km圆环内.噪声源在一段时间内均匀随机振动,然后合成相应的背景噪声,共60段,其中一段噪声如图4b所示.接着对噪声进行处理,合成互相关函数,并得到互相关函数实数部分,然后利用共轭梯度算法反演地下模型,在反演中初始模型选择速度递增背景速度场,反演结果如图5所示.
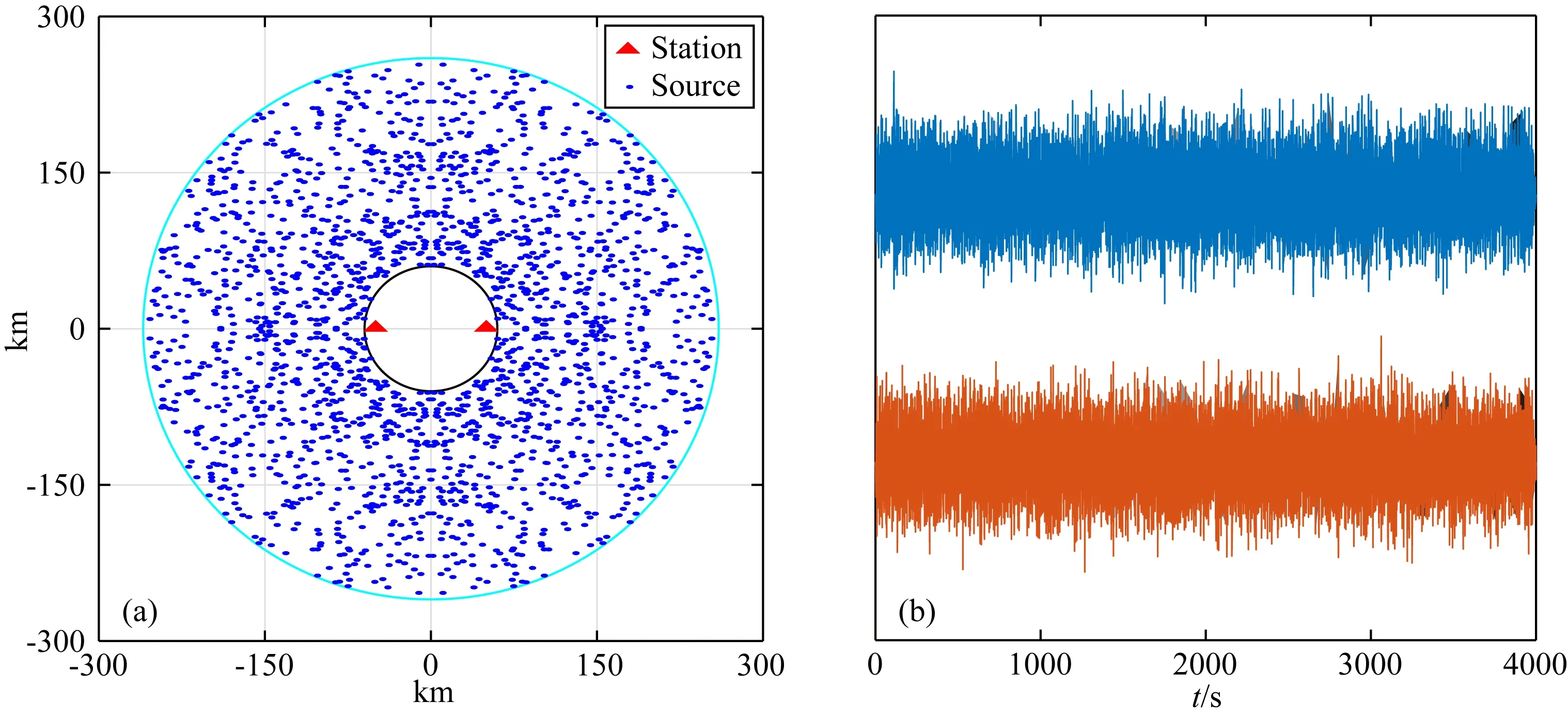
图4 (a)噪声源与台站之间的相对位置关系;(b)模拟的背景噪声
图5a为L曲线法确定正则化参数,由于数据误差中包含权重因子,因此其值较大.从图5b、5c、5d可以看出,反演结果虽然在具体数值上与真实结果有一定偏差,但形态特征基本与真实模型一致.其结果大体上可以反映出真实的地下结构.
2.2 实际数据模型测试
接着对一段实际资料进行处理研究,实际资料来源于中国永丰—抚州断裂地区(赵延娜等,2015).该区及附近区域地下岩石圈软流圈边界主要分布范围为85~150 km范围之间(Hu and Wang,2000;Priestley and McKenzie,2013;Ouyang et al.,2014;Shan et al.,2017),不同观测和定义方法可能会有一定误差,但地下软流圈的存在基本已无争议.此处选择台站SC09和SC19噪声数据进行反演,台站间距约为100 km,使用频段范围为0.06~0.11 Hz,共划分0.06~0.08 Hz,0.07~0.09 Hz,0.09~0.11 Hz三个频段,初始模型层厚3 km是一递增模型.将反演结果与频散曲线结果进行对比,验证方法正确性.反演结果如图6所示,其中图6a为正则化参数,图6b为反演结果,图7—9为三个频段下,互相关函数比较结果,其中(a)表示实际互相关与由初始模型计算得到互相关比较结果,图(b)表示实际互相关与由反演结果计算得到互相关比较结果,图(c)表示真实互相关与初始模型误差,图(d)表示真实互相关与反演结果误差.图10为初始模型计算得到的频散曲线(蓝线)和反演结果计算得到的频散曲线(红线)与FJ方法(图10a)和双台时频分析(图10b)提取的频散曲线之间的比较结果,与初始模型相比本文反演结果计算得到的频散曲线在对应频段能更好的与实际频散曲线拟合.从互相关函数和频散曲线比较结果中可以看出,反演结果误差相比于初始误差是减小的,反演结果是朝着真实结果收敛的.从而在实际资料中验证了本文方法的可行性.
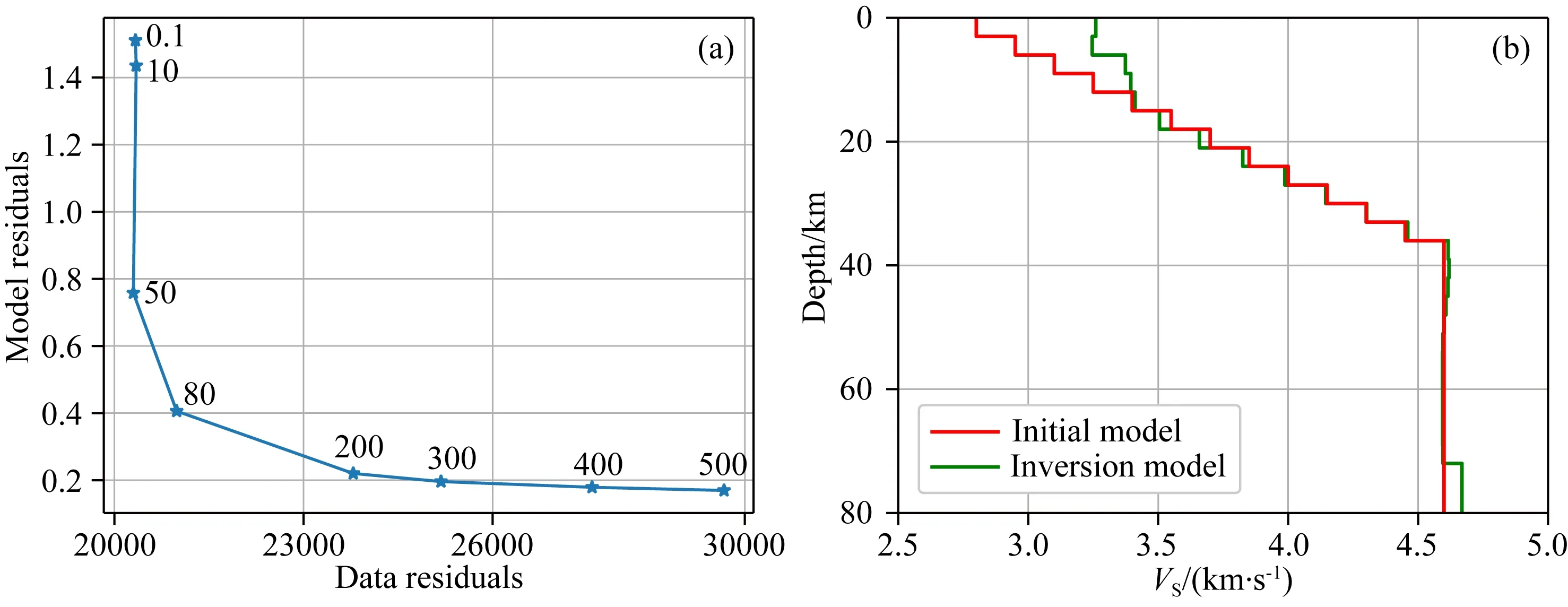
图6 (a)L曲线示意图;(b)初始模型与反演结果示意图
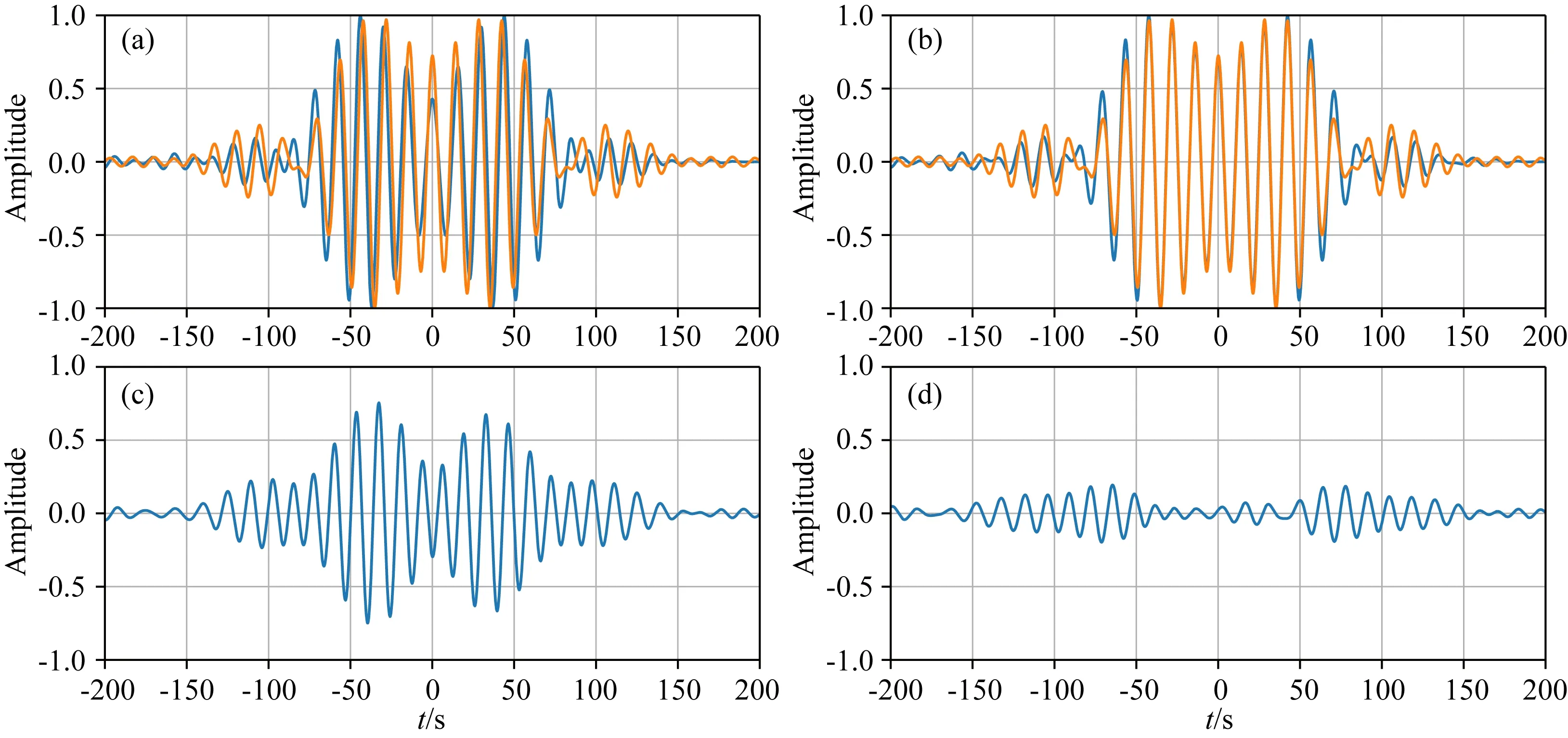
图7 频段为0.06~0.08 Hz时(a)真实数据与初始模型合成数据比较;(b)真实数据与反演结果合成数据比较;(c)真实数据与初始模型合成数据差;(d)真实数据与反演结果差
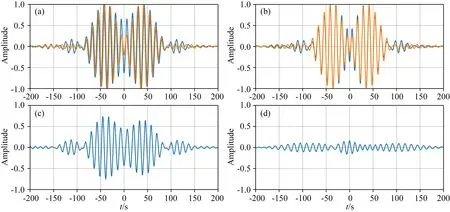
图8 频段为0.07~0.09 Hz时(a)真实数据与初始模型合成数据比较;(b)真实数据与反演结果合成数据比较;(c)真实数据与初始模型合成数据差;(d)真实数据与反演结果差
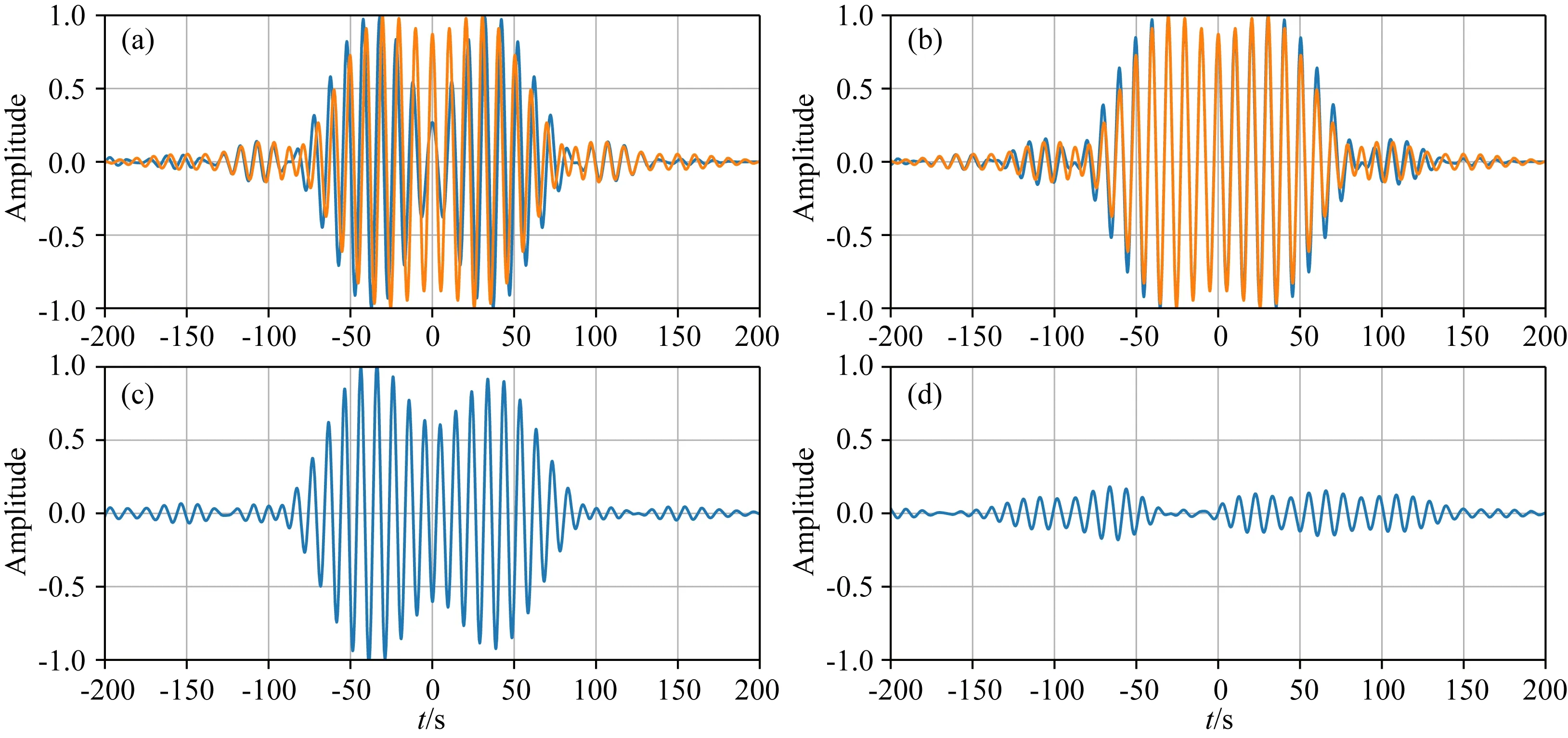
图9 频段为0.09~0.11 Hz时(a)真实数据与初始模型合成数据比较;(b)真实数据与反演结果合成数据比较;(c)真实数据与初始模型合成数据差;(d)真实数据与反演结果差
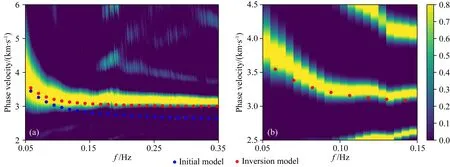
图10 本文反演结果(红线)和初始模型结果(蓝线)与基于频率贝塞尔函数提取频散曲线(a)和时频分析提取频散曲线(b)对比说明图
本文敏感性分析表明,由于不同频段互相关函数对不同尺度和深度模型敏感性不同,因此我们可以选择新的反演方案.在同一台站间距尺度下,给定一个层厚较大,深度较深的初始模型,接着用较低频段进行反演,此时可以得到大尺度模型反演结果.接着对反演结果重新划分层厚,并将其作为初始模型,用高频段信息进行反演,从而得到更加精细的结果.与前人多尺度反演方法的不同之处在于本文对层厚进行了重新划分,可以得到更加精细的模型结果.
首先,对原模型划分层厚,层厚为6 km,用较低频段进行反演,反演频段为0.05~0.07 Hz,0.06~0.08 Hz,0.07~0.09 Hz,大尺度模型反演结果如图11所示.
从图11a可以看出本文反演结果在110 km处左右可见明显低速异常,基本在该地区软流圈范围内.频散曲线对比结果中红色点表示由初始模型计算得到的结果,蓝色点表示由反演结果计算得到的结果.从图11b中可以看出,蓝点与实际提取得到的频散曲线能较好的拟合.从而说明反演结果可靠性.
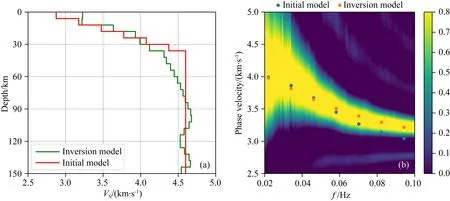
图11 (a)反演结果与初始模型示意图;(b)反演结果(蓝线)和初始模型(红线)与频散曲线比较结果
为了验证反演深度可靠性,我们对上面反演结果(不包含最底层无穷远半空间)在对应反演频段下进行敏感性分析.此处协方差矩阵由实际资料处理得到.从图12敏感性结果可以看出,本文所选择频段对深部异常结构具有敏感性,说明了反演深度可靠性.在实际反演中反演结果通常取决于实际资料中的有效信号,而协方差矩阵可以有效衡量有效信号.
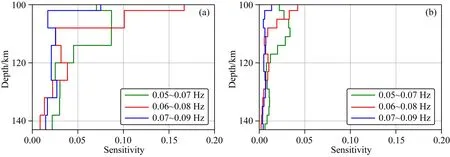
图12 反演结果模型不同层厚在三个频段下深部结构敏感性结果
2.3 多尺度反演
接着根据不同频率对不同层厚和深度敏感性不同,验证本文模型尺度随频率变化而变化的多尺度反演方法的有效性.将前面反演结果作为初始模型,对原6 km层厚进行重新划分,划分为3 km层厚,划分过程类似于图14a到图14b,保留对应深度具体数值不变,然后用较高频率进行反演.反演结果如下:
从图13中可以看出,当加入较高频率后,高频主要对浅层结构敏感,可以反演得到更加精细的浅层结果.由于在反演时我们无法确定基于层状假设合适频段,因此,此处给出了两个频段进行反演.由于频段不一样,且浅部结构较为复杂,层状近似误差较大,因此在数值上略有区别,但两个高频段数据对浅层反演结果都可见浅部低速异常结构.此低速构造可能是该区断裂带的存在导致油气水或地下岩浆等低速体的聚集导致.通常在一维结构反演中我们可以给定一系列初始模型从而求得相对稳定的反演结果.在二维、三维反演中由于计算量的限制,通常很少采用该方法.本方法可以为复杂介质成像构建相对可靠初始模型.
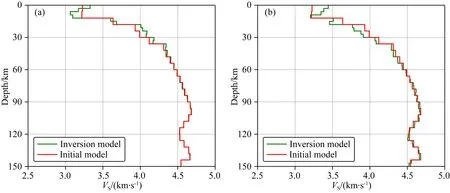
图13 (a)0.06~0.1 Hz中三个频段数据反演结果;(b)0.07~0.11 Hz中三个频段数据反演结果
接着对上述结果进行解释.
如图14所示,对于地下10~20 km处一个异常体,保持台站间距不变,如图14b对层厚进行重新划分,层厚较大时,异常体相对影响较小,层厚较小时,异常体相对影响较大.因此,层厚和台站间距等均会对结果产生相应影响,而本文多尺度方法可以得到相对准确的异常体层位信息.另一方面,如图14b所示,对于低频长波长信息,较小的层厚占波长比重较小,因此对模型敏感性较小,只有通过增加层厚才能反演得到相对精确的结果,同时也可以将低频反演结果作为高频反演初始模型,从而反演得到更加精细的结果.图14主要说明合理划分层厚,选择合适的台站间距、频率对于研究不同尺度地下介质真实结构具有较为重要作用.这一结论和假设,即成像频率逐渐变大,尺度逐渐变小,广泛存在于弹性波成像中,如大尺度地震成像,地震勘探,超声医学成像中.
图14理论分析表明,对于各向同性层状介质假设方法,仅在地下介质完全均匀情况下才有可能反演出相对真实的参数结果.当地下含有异常体时,反演参数值是地下介质参数的一个平均结果,层厚的划分对模型分辨率结果具有一定影响.
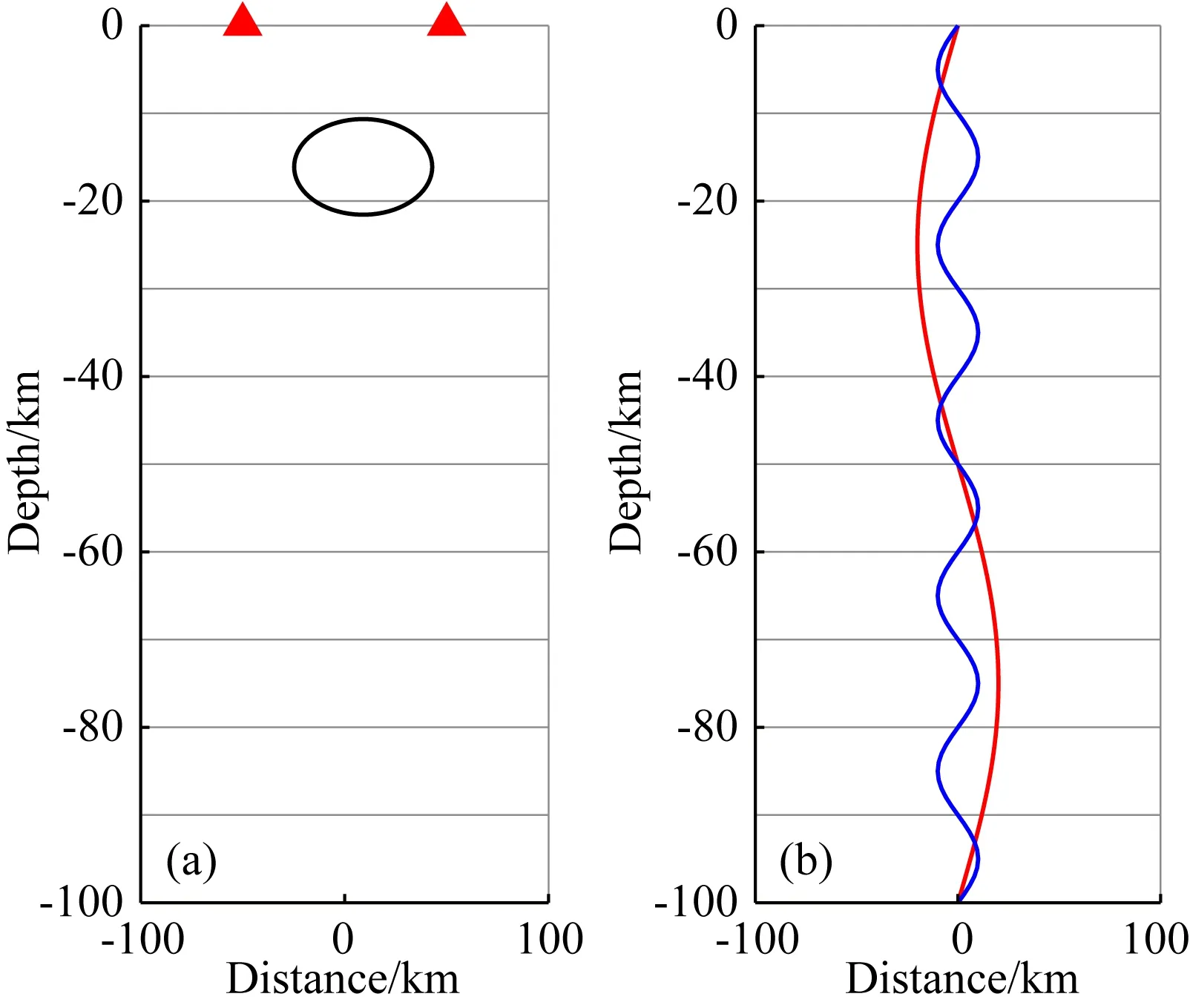
图14 (a)层厚为20 km示意图;(b)层厚为10 km不同频率波长数据对地下介质响应示意图
3 结论
本文在各向同性层状介质假设下基于背景噪声互相关函数成像提出了层厚和反演深度随频率变化的多尺度成像方法.本文反演主要是在单一台站间距下,利用低频反演大尺度模型,然后对低频反演结果重新划分层厚添加高频成分反演得到更精细的结果,这样可以权衡计算量、模型分辨率、反演稳定性和反演深度之间的关系.本文方法为今后二维、三维反演获得相对可靠初始速度模型以及为多尺度反演提供了相应策略.同时对仅能布设少量地震台站的地区如月球火星等地外天体内部结构探测具有较为重要的意义.
致谢感谢2020北大暑期课程以及课题组提供的噪声处理开源程序,同时感谢课题组陈举庆、闫英伟、康佳语、徐建宽和李正波等人在文章修改过程中提供的文字润色和校正服务.
