基于射线理论点扩散函数的成像域最小二乘偏移
2023-02-11岳玉波秦宁杨哲陈祥忠徐云贵曹卫平唐静
岳玉波,秦宁,杨哲,陈祥忠,徐云贵,曹卫平,唐静
1 页岩油气富集机理与有效开发国家重点实验室,北京 102206 2 西南石油大学地球科学与技术学院,成都 610500 3 中国石化胜利油田物探研究院,东营 257022 4 中国石油勘探院西北分院,兰州 730020 5 山东理工大学资源与环境工程学院,淄博 255000
0 引言
作为地震数据处理中的关键技术环节之一,地震成像技术在日趋复杂化和精细化的油气勘探过程中发挥着重要作用.理论上来说,地震成像方法不仅需要具备精确构造成像的能力,还需要具备岩性成像能力以保证地震反演和储层预测的精度(Claerbout, 1971; Bleistein et al., 2001).然而,传统的地震成像方法只是线性正演算子的共轭转置,对于有限观测系统采集的带限地震数据,只能得到模糊的构造成像结果(Tarantola, 1984; Yu et al., 2006; 岳玉波等, 2012; 刘玉敏等, 2021).此外,复杂的地下介质构造和非规则的地震数据采集,还会导致偏移假象和非均匀的成像照明,严重影响成像振幅的可靠性.
基于线性地震反演理论的最小二乘偏移技术(Least-Squares Migration, LSM)是解决上述问题的有效途径(Tarantola, 1984; Nemeth et al., 1999).该技术将地震偏移成像视为线性反问题并利用最优化方法进行迭代求解,理论上能够消除非规则采集、带限子波等因素对成像结果造成的不良影响,提高成像分辨率和振幅保真度.然而,该技术的理论优势并没有充分转化成为实际的应用效果,其主要原因之一在于计算成本过于高昂.经典的数据域LSM(Nemeth et al., 1999; Duquet et al., 2000; Dai et al., 2011; Yue et al., 2019, 2021a,b; 杨宏伟等, 2022)通过反演迭代使模拟数据逐步逼近实际地震数据,进而实现地下反射率的准确估计.该方法每次迭代都需要一次正演和偏移运算,整体反演过程所需的计算成本往往在常规偏移的几十倍以上,严重制约了该方法的推广应用前景.成像域迭代算法也是目前常用的LSM实现方法,该方法假定Hessian矩阵可以描述地震成像系统对地下介质的模糊效应(Jansson, 1997; Lecomte, 2008; Jensen et al., 2021),在通过反演迭代校正Hessian矩阵的模糊效应后便可获得地下真实的反射率.成像域LSM的核心是Hessian矩阵的求取,然而由于Hessian矩阵的规模十分庞大,其计算和存储过程依然是一项巨大的挑战(Valenciano et al., 2009; Tang, 2009; Jiang and Zhang, 2019).
Hessian矩阵是一个主对角占优的带状矩阵(Ren et al., 2011; 任浩然等,2013),因此可以在不失精度的前提下,通过保留主对角线附近的部分非对角元素来降低Hessian矩阵的计算和存储成本,这种局部化的Hessian矩阵也称作点扩散函数(Point Spread Function, PSF).Fletcher等(2016)、Osorio等(2021)、段伟国等(2022)、Mao等(2022)、陈生昌等(2022)提出通过串联的正演+偏移运算来获取地下稀疏空间位置的PSF场,然后通过插值构建任意空间位置的PSF,该过程的计算成本约为两次常规偏移,但在实际应用中却存在如下问题.PSF是同地震速度、观测系统等因素相关的非平稳空间信号,当地下介质速度变化平缓、地震观测系统较为规则时,使用较大的PSF采样间隔即可满足插值精度;当地下介质速度变化剧烈、观测系统非规则性很强时,则需要使用较为密集的PSF空间采样,但密集的空间采样往往会导致相邻PSF间的交叉串扰,因此在实际应用中往往需要多次计算PSF场,使得计算成本大幅提高.Jiang和Zhang(2019)、Xu等(2022)提出利用地震射线理论求解格林函数,并以此为基础进行PSF的直接解析计算.该算法的计算实现过程类似于Kirchhoff偏移,能够适应任意的PSF场空间采样,但计算成本依然至少在一次常规Kirchhoff偏移以上.
本文在上述射线理论PSF直接算法的基础上,提出了一种更为高效的PSF快速算法.该算法利用地震波走时一阶近似对PSF的计算过程进行优化,大幅提升了计算效率.以此为基础,本文进一步发展了基于PSF的成像域LSM,能够高效、灵活地实现地下反射率的迭代更新,获得分辨率更高、照明更加均衡的反演成像结果.文中通过模型和实际数据的试算对PSF快速算法的计算精度和效率以及成像域LSM的应用效果进行了验证.
1 方法原理
本节首先对PSF直接算法的基本原理进行简要介绍,接下来给出本文快速算法的推导实现过程并对两种算法的计算效率进行对比分析,最后基于PSF构建成像域LSM迭代反演流程.
1.1 基于射线理论的PSF直接算法
基于地震散射理论(Tarantola, 1984),线性Born正演算子可以表示为:
×G(x0,xs,ω)dx0,
(1)
其中,xs和xr分别代表震源和接收点的空间位置,F(ω)是震源子波函数,m(x0)是散射点x0处的散射强度(Hu et al., 2016),V代表地下散射点的集合,G(x,x′,ω)是震源位于x′、观测点位于x的格林函数.通过求取式(1)的共轭转置,可以得到相应的共轭偏移算子:
×G*(x,xs,ω)d(xr,xs,ω)dxrdxs,
(2)
其中,m′(x)代表地下成像点x处的成像结果,符号*代表复共轭运算.
将式(1)代入式(2),可以得到成像结果m′(x)同地下真实散射强度m(x0)之间的关系:
(3)
其中,H(x,x0)为Hessian矩阵,具有如下的形式:
×G(x0,xr,ω)G(x0,xs,ω)dxrdxs,
(4)
Hessian矩阵描述了复杂速度、非规则地震采集、带限子波等因素造成的地震成像系统对地下介质的模糊效应,因此常规偏移只能得到模糊化的构造成像结果.
直接采用波动方程的数值解计算式(4)中的格林函数需要耗费高昂的计算和存储成本.为提高计算效率,可以采用高效、灵活的地震射线理论进行格林函数的计算:
G(x,x′,ω)=a(x,x′)exp[iωt(x,x′)],
(5)
其中,a(x,x′)和t(x,x′)分别为地震波的振幅和走时,深度域的走时和振幅信息可以分别通过运动学和动力学射线追踪求取,在时间域计算则可以使用Zhang等(2000)提出的简化算法.将式(5)代入式(2)即可得到常规Kirchhoff积分偏移公式.将式(5)代入式(4),并应用傅里叶逆变换可得:
H(x,x0)=∬a*(x,xr)a*(x,xs)a(x0,xr)a(x0,xs)
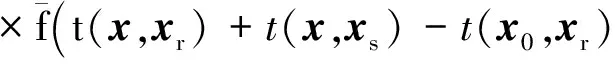
-t(x0,xr))dxrdxs,
(6)
其中:
(7)
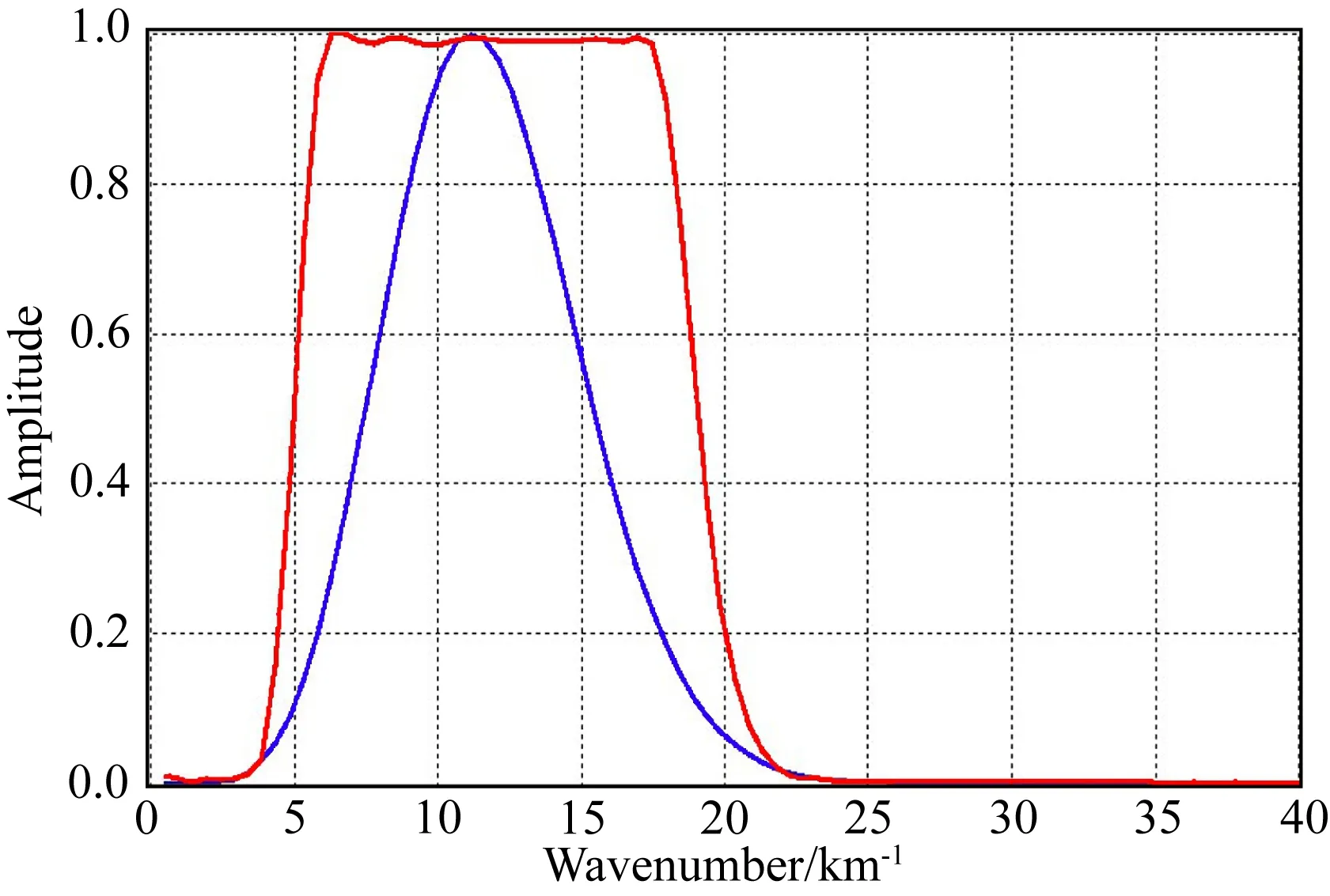
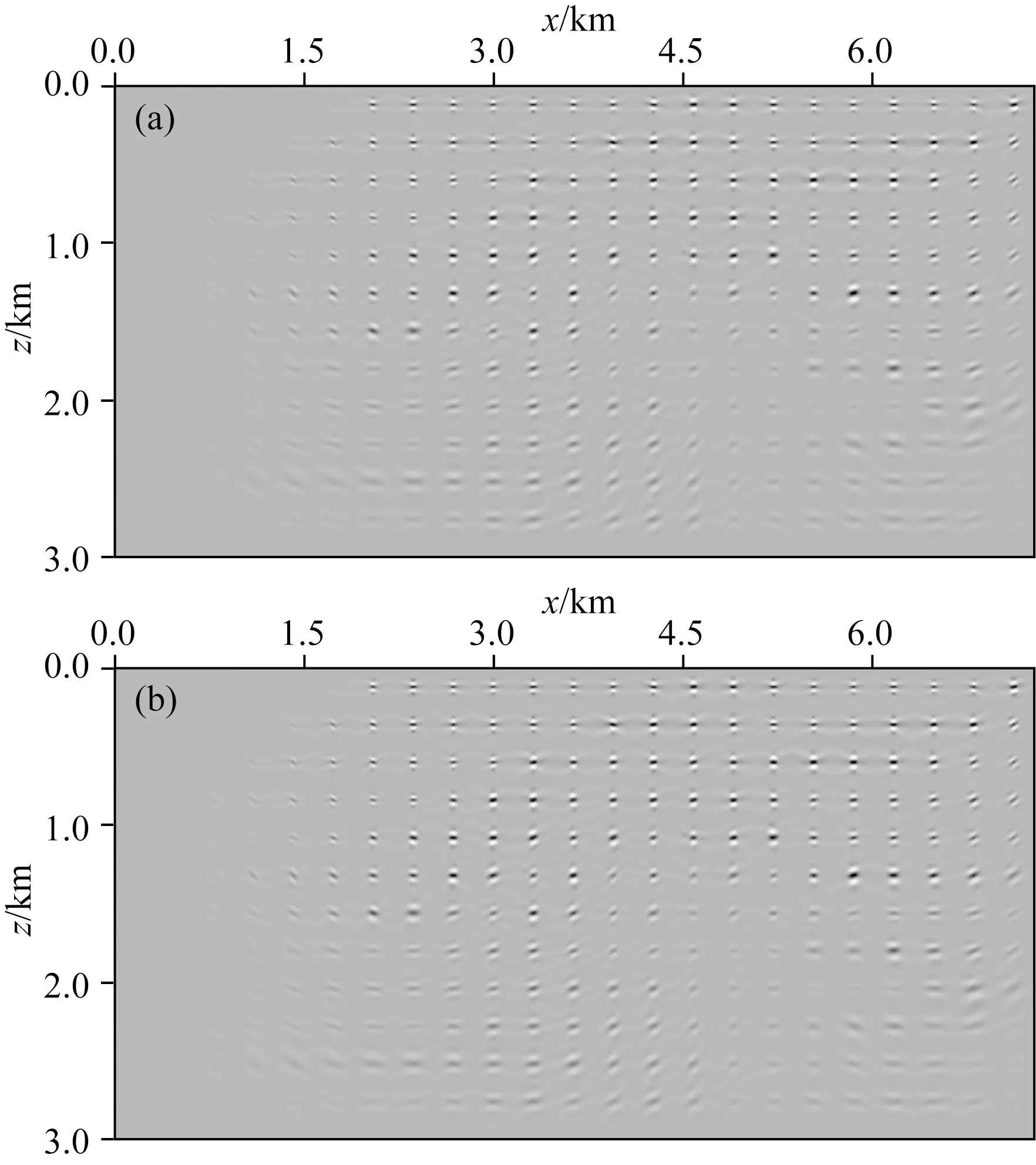
式(7)为地震子波的自相关函数.考虑到Hessian矩阵的能量主要集中在主对角线附近,因此可以只保留成像点x(PSF中心点)附近满足x0=x+Δx,|Δx| (8) 其中,H(x,x+Δx)是中心点x处的局部化Hessian矩阵,也称作PSF(Jansson, 1997; Lecomte, 2008),具有如下的形式: H(x,x+Δx)=∬a*(x,xr)a*(x,xs)a(x+Δx,xr)a(x+Δx,xs) (9) 式(9)即为射线理论PSF直接算法公式,其计算过程同Kirchhoff偏移非常接近,区别主要在于走时项的计算方式.由于计算过程相互独立,上述算法能够适应任意的PSF场空间采样,其计算成本正比于PSF场的总采样点数,耗时至少在一次常规Kirchhoff偏移以上. 为进一步提高PSF的计算效率,本文在上述直接算法的基础上,利用地震波走时一阶近似对PSF的计算过程进行优化,发展了如下的快速算法. 由于PSF的有效样点x+Δx分布在中心点x附近,那么可以将x+Δx处的地震波走时用x处走时的一阶泰勒展开来近似表示(如图1所示): 图1 地震射线参数与走时近似 t(xs,x+Δx)≈t(xs,x)+ps·Δx,t(xr,x+Δx) ≈t(xr,x)+pr·Δx, (10) 其中,ps和pr分别为中心点x处的震源和接收点射线参数.将式(10)代入式(9),并假定: a(x+Δx,xs)≈a(x,xs),a(x+Δx,xr)≈a(x,xr), (11) 那么式(9)可以近似表示为: ×dxrdxs, (12) 其中,pm=ps+pr是x处的中心点射线参数. (13) (14) (15) 其中,x′r和x′s分别为对应的震源和接收点. 接下来对比分析两种PSF算法的计算效率.假设中心点x处PSF的采样点数为Npsf,计算孔径内的地震记录道数为Ntr,那么PSF直接算法的计算成本可以估算为: (16) Cfast=Ntr×Oamp+Npsf×Np×Oker, (17) 在求取PSF场后,可以通过线性插值高效计算地下任意空间位置的PSF.以此为基础,我们构建了如下的成像域LSM目标函数(Osorio et al., 2021): (18) 其中,m为待求的地下反射率,H为求取的PSF场,m′为Kirchhoff偏移结果,J(m)是以L2模定义的数据匹配项,R(m)是用来保证反演过程稳定的正则化项,本文在此使用的是Tikhonov正则化(Nemeth et al., 1999),μ是正则化权系数,一般需要多次试验来确定.式(18)的求解过程一般通过共轭梯度法等梯度类迭代算法进行实现,其计算成本相比于m′的计算过程可以忽略不计.因此,以PSF快速算法为基础发展的成像域LSM具备极高的计算效率,所需的计算成本(包括PSF计算和反演迭代过程)远低于一次常规Kirchhoff偏移(通常在20%以内). 本节首先采用水平层状模型和Marmousi模型进行测试,对比两种PSF算法的计算精度和效率,并验证成像域LSM的正确性和有效性;接下来采用某探区二维数据进行测试,检验成像域LSM对于实际地震数据的应用效果. 层状模型网格大小为480×375,纵横向采样间隔分别为10 m和8 m.假设模型速度为常速2000 m·s-1,在深度为0.8 km、1.6 km、2.4 km处分别布设了三个反射系数为1的水平反射界面.通过计算反射时距曲线并同主频为25 Hz的雷克子波进行褶积合成了120炮记录,每炮121道,炮间隔和道间隔为均为30 m.图2展示了该数据的Kirchhoff深度偏移结果,其中沿其反射界面提取的振幅曲线如图3所示,可以看到虽然常规偏移能够对反射界面进行正确归位,但由于受到几何扩散、非均匀数据覆盖等因素的影响,成像振幅严重失真. 图2 Kirchhoff深度偏移结果 图3 沿图2反射界面提取的振幅曲线 分别应用直接算法和快速算法进行PSF场的计算,其结果如图4a和图4b所示.图5a—d进一步放大对比了中心点在x=2.1 km,z=1.3 km处和x=3.3 km,z=1.9 km处的局部PSF计算结果,可以看到不论对于整体PSF场还是对于单点PSF,两种算法的计算结果都非常接近,两者的相对误差仅为4%左右,且主要集中在PSF的旁瓣,并不会对LSM反演产生影响.统计对比两种PSF算法的计算时间,其中直接算法的耗时约为251.3 s,高效算法的耗时为24.7 s(不足直接算法的1/10),由此可见本文提出PSF快速算法可以在保证计算精度的同时大幅提升计算效率.利用常规偏移剖面和PSF场作为输入进行成像域LSM处理,20次迭代后的归一化数据残差约为3%,最终的反演成像结果如图6所示(图中 “振铃”状的成像旁瓣是拓展成像频带导致的吉布斯现象).为更好地评估其效果,图7展示了沿反射界面提取的振幅曲线,图8对比了反演前后的成像波数谱,可以看到成像域LSM取得了预期的应用效果,其不但准确恢复了界面的真实反射系数,还明显拓宽了成像波数,提高了成像分辨率. 图4 不同方法求取的PSF场 图5 中心点在不同空间位置的局部PSF对比 图6 成像域LSM结果 图7 沿图6反射界面提取的振幅曲线 图8 成像波数谱对比 Marmousi模型速度场如图9所示,网格大小为737×750,纵横向采样间隔分别为10 m和4 m.利用有限差分法正演了240炮地震记录,炮点位于地表,初始炮点位于x=2.5 km处.炮间隔为20 m,每炮120道单边接收,道间隔也为20 m,震源函数为主频20 Hz的雷克子波.图10a和图10b分别展示了利用直接算法和快速算法求取的PSF场,其中中心点位于x=3.0 km,z=0.8 km处和x=5.5 km,z=1.3 km处的局部PSF对比结果如图11所示.可以看到即便对于复杂的Marmousi模型,快速算法也可以得到媲美直接算法的计算结果,但其计算效率(耗时81.6 s)相比直接算法(耗时493.2 s)具有明显的优势. 图9 Marmousi模型速度场 图10 Marmousi模型PSF场 图11 中心点在不同空间位置的局部PSF对比 接下来对正演记录进行Kirchhoff深度偏移处理,所得到的成像结果如图12a所示.可以看到虽然其较为准确地恢复了模型的主要构造信息,但成像分辨率较差、成像照明不均.利用PSF场对偏移剖面进行成像域LSM处理,25次迭代后的归一化数据残差约为10%,最终的反演成像结果如图12b所示.可以看到其不但明显提升了成像分辨率,还有效改善了地下成像照明.图13提取了x=3.1 km处的成像道波形(红色曲线)并同真实反射率(蓝色曲线)进行对比,可以看到常规偏移结果同真实反射率存在很大的偏差(图13a),成像波形和振幅严重失真,而成像域LSM(图13b)则大幅提升了成像分辨率和振幅保真性. 图12 Marmousi模型成像结果对比 图13 x=3.1 km处成像道波形(红色曲线)同理论反射率(蓝色曲线)对比 实际数据的偏移测试在时间域进行,其均方根速度场如图14所示,网格大小为800×750,纵横向采样间隔分别为4 ms和12.5 m.将主频为25 Hz的雷克子波作为震源信号进行PSF场的计算,所得到的结果如图15所示.可以看到PSF场的能量中间强、两侧弱,同地震数据的空间覆盖分布具有很好的对应性. 图14 均方根速度场 图16a展示了该数据的Kirchhoff时间偏移结果,可以看到其能量分布特点同图15所示的PSF场基本一致.利用PSF场对偏移剖面进行成像域LSM处理,20次迭代后的反演成像结果如图16b所示.可以看到成像域LSM有效补偿了剖面两侧的成像照明,成像分辨率也得到了明显的提升.在图17所示的局部成像对比以及图18所示的成像频谱对比中可以看到,成像域LSM明显拓展了成像频带,不但具有更高的薄层分辨能力(图17红色箭头),其补偿的低频信息还有效增强了成像连续性(图17红色方框). 图15 PSF场 图16 成像结果对比 图17 成像剖面局部对比 图18 成像频谱对比 LSM是当前地震成像技术重要的研究和发展方向,但庞大的计算成本严重制约了其的应用前景.本文基于射线理论格林函数和地震波走时一阶近似,提出了一种快速的PSF计算方法,不但可以获得媲美原有算法的PSF计算结果,还具有明显的计算效率优势.以此为基础发展的成像域LSM能以明显低于常规偏移的计算成本实现地震成像剖面的迭代更新,获得高分辨率、高保真的反演成像结果,有望成为一种切实可行的LSM实施方案.接下来,我们会将本文工作进一步拓展到三维,并研究使用L1、TV等正则化算法以及合理的预条件算子,进一步优化本文LSM的成像效果和计算效率.1.2 PSF快速算法

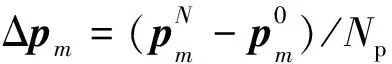


1.3 算法效率对比




1.4 成像域最小二乘偏移
2 模型及实际资料试算
2.1 层状模型试算






2.2 Marmousi模型试算



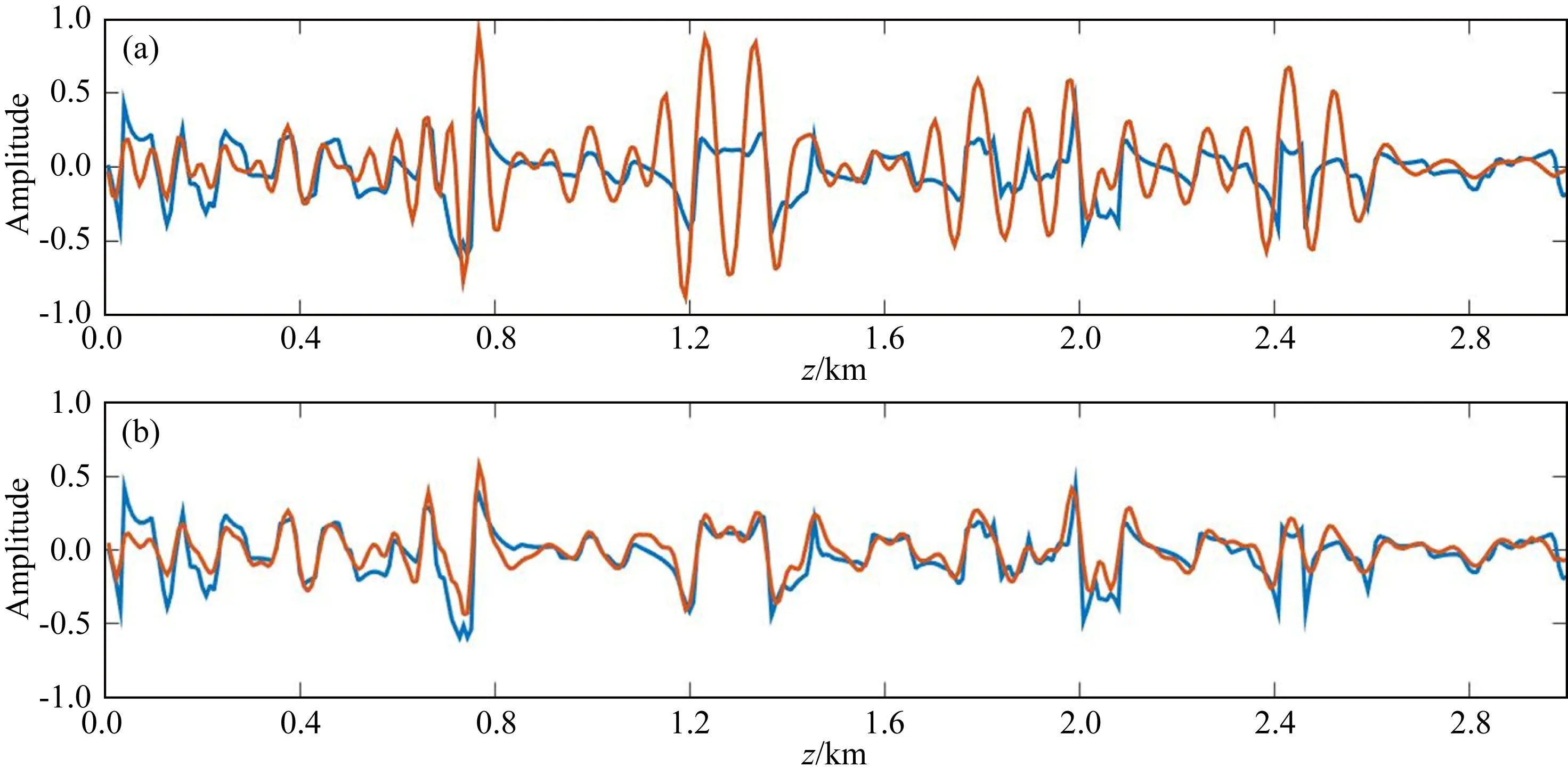
2.3 实际数据试算



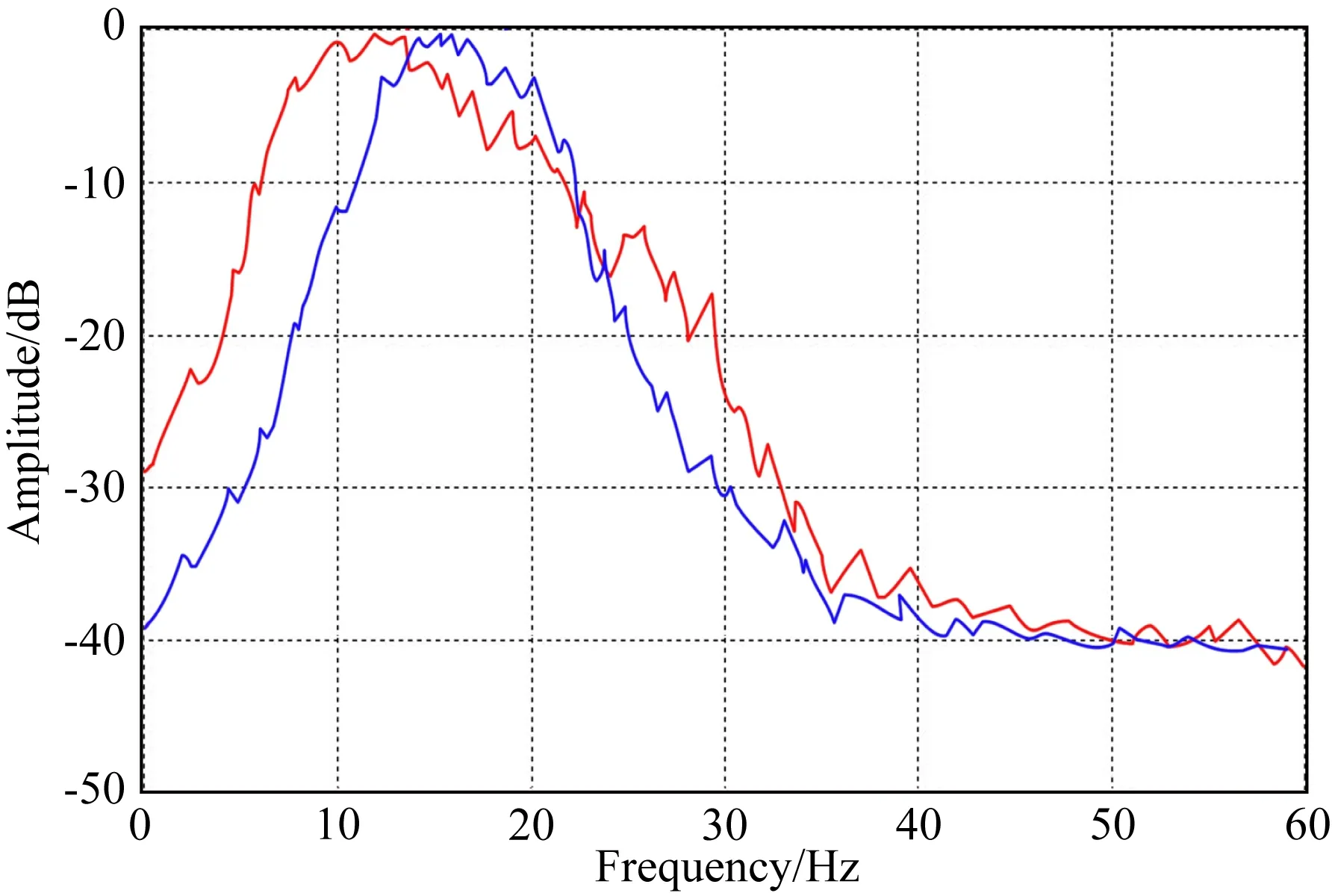
3 结论
