分布式光纤声波传感微振动响应特征

姚艺, 王一博，王伟君，陈凌

1 中国科学院地质与地球物理研究所, 北京 100029 2 中国科学院大学，北京 100049 3 中国地震局地震预测研究所，北京 100036

0 引言

分布式光纤声波传感技术(Distributed Acoustic Sensing, DAS)是一种新型的地震采集技术.它利用光纤既是传输介质也是传感设备这一优势，获取光纤上每一点的应变/应变率.其主要工作原理是，外部扰动(如地震波等)引起光纤中微小不均匀体的位置发生变化，从而导致光纤中的散射光信号发生变化，通过解调散射光信号便可以获得沿光纤上每个点的应变信息(Parker et al., 2014).

相较于传统的检波器，DAS具有以下优点：首先是高密度数据采样，DAS可以达到米级的空间采样率，对观测区域的覆盖密度更高，只要布设一条光缆，就可以获得数千上万个地震观测点；其次，DAS的传感介质是光纤，光纤本身成本低廉，适用于长距离布设；最后，光纤还具有耐高温和耐腐蚀性等特性，可以永久性布设，长时间采集地震数据.

DAS的应用领域非常多，已经从早期的定性测量，比如周界入侵、油气管道安全监测等，逐渐发展为定量测量.井中监测是DAS最早的地震学应用，主要包含垂直地震剖面成像(Bakku et al., 2014)、微地震监测(Lellouch et al., 2020)等.DAS在近地表结构以及城市地下空间探测中也发挥了重要作用，如通过DAS噪声分析可以获得500 m以内的浅层结构信息(Shragge et al，2021).此外，DAS还应用于火山(Nishimura et al., 2021)、冰川(Walter et al., 2020)等地震监测中.

DAS与传统的三分量检波器不同，其对沿着光纤轴向方向敏感.因此DAS能够提供单分量的地震数据，且这些数据与地震波的传播方向和振动方向相关.地震勘探已经逐渐开始使用三分量地震数据进行成像等工作，因此亟需三分量的分布式光纤声波传感技术.有学者提出通过设计螺旋缠绕的光缆结构，实现地震波场的三分量应变测量(Ning and Sava, 2018; Innanen et al., 2019; 曹丹平等，2022).

尽管DAS已经在地震勘探等领域得到很多应用，但还有一些理论知识有待研究.本文致力于研究DAS的应变辐射花样及微振动响应特征，首先通过理论推导获取应变辐射花样，分析其与速度辐射花样的区别；然后通过数值模拟，展示不同震源机制情况下的应变辐射花样以及不同测线的DAS微振动响应.

1 震源模型

震源模型主要包含单力源模型及力偶模型，其中单力源模型中的震源是某个方向的作用力，比如锤击实验中的锤击震源.力偶模型中的震源通常是一对方向相反的作用力，一般用矩张量来表示(Gilbert, 1970).震源矩张量可分解为各向同性震源(Isotropic，ISO)、双力偶震源(Double Couple，DC)以及补偿线性矢量偶极子震源(Compensated Linear Vector Dipole, CLVD)(Knopoff and Randall，1970).各向同性震源用归一化单位矩阵表示，代表爆炸震源或者压缩震源，在各向同性均匀介质中只产生P波.双力偶震源也即剪切震源，是较为常见的震源模型.CLVD震源一般与ISO震源共存，不涉及体积变化，其某个轴的膨胀(压缩)会被另两个轴的压缩(膨胀)进行补偿.

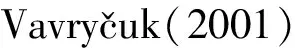
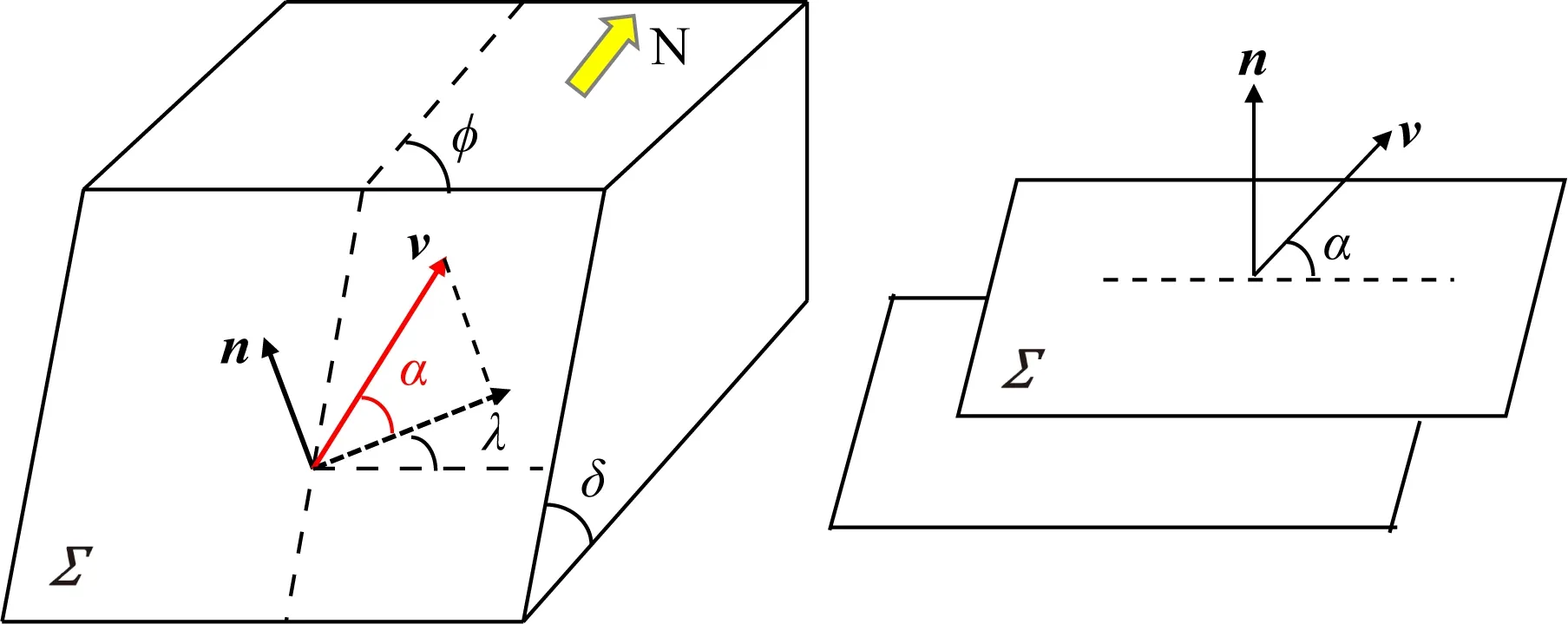
图1 一般位错模型示意图

(1)

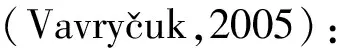
Mij=cijklDkl,

(2)

(3)

由式(2)可知，震源区的矩张量不仅与所处区域的弹性参数有关，也与断层滑移的方向有关.通过设计不同的震源参数，可以得到不同的震源模型.

2 微振动辐射花样

单力源的位移记录表达式为(Aki and Richard，2002)：

(4)

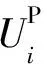
(5)

(6)

由于应变是位移的空间导数，为此通过位移对空间方向进行求导，可以得到应变的数学表达式：

(7)

f(xi)=xixp,

(8)

g(xi)=r-3,

(9)

(10)

根据求导法则，可推导单力源的P波应变为：

(11)

在式(11)中，前半部分与1/r2成正比，为中场项，后半部分与1/r成正比，为应变的远场项.同样对应变的辐射花样选取远场项部分，将上述方法应用于单力源的S波可以得到：

(12)

因此单力源的P波和S波的应变辐射公式为：

(13)

(14)

类似地，根据Aki和Richard(2002)的位移计算可知，矩张量产生的位移场包含近场项、中场项以及远场项.Song和Toksöz(2011)认为远场项在大约1.5个波长距离后成为主导项.因此对于辐射图案的分析，也都是选择远场项.在均质、各向同性介质中，由矩张量震源引起的P波位移的表达式为：

(15)

其中远场项可表示为：

(16)

(17)

位移辐射花样表达式为：

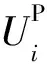
(18)

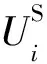
(19)

将位移对空间方向求导，可得P波应变的表达式：

(20)

同理，S波的应变表达式为：

(21)

同样选取远场项，矩张量震源的应变辐射花样公式为：

(22)

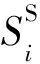
(23)

表1列出了本文所用的震源模型，其中后5种震源均包含DC分量.图2—图9展示了表1对应震源模型的P波和S波在x1x3平面上的速度辐射花样和应变辐射花样.

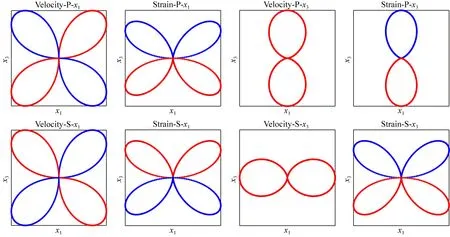
图2 单力源在x1x3平面内x1和x3分量的速度辐射花样和应变辐射花样

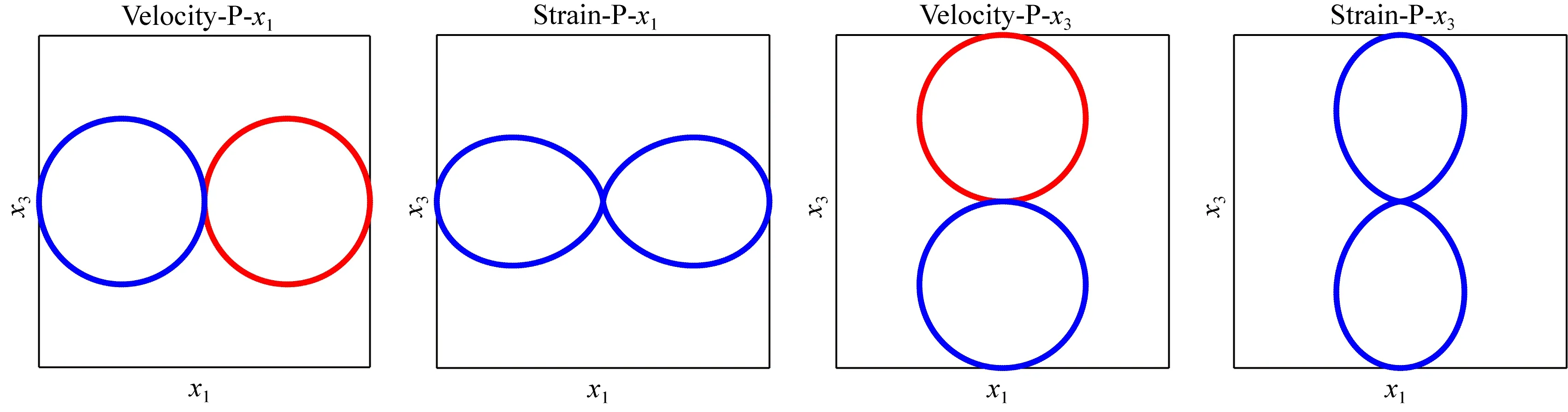
图3 ISO震源在x1x3平面内x1和x3分量的速度辐射花样和应变辐射花样

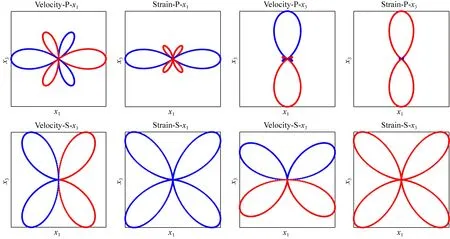
图4 CLVD震源在x1x3平面内x1和x3分量的速度辐射花样和应变辐射花样

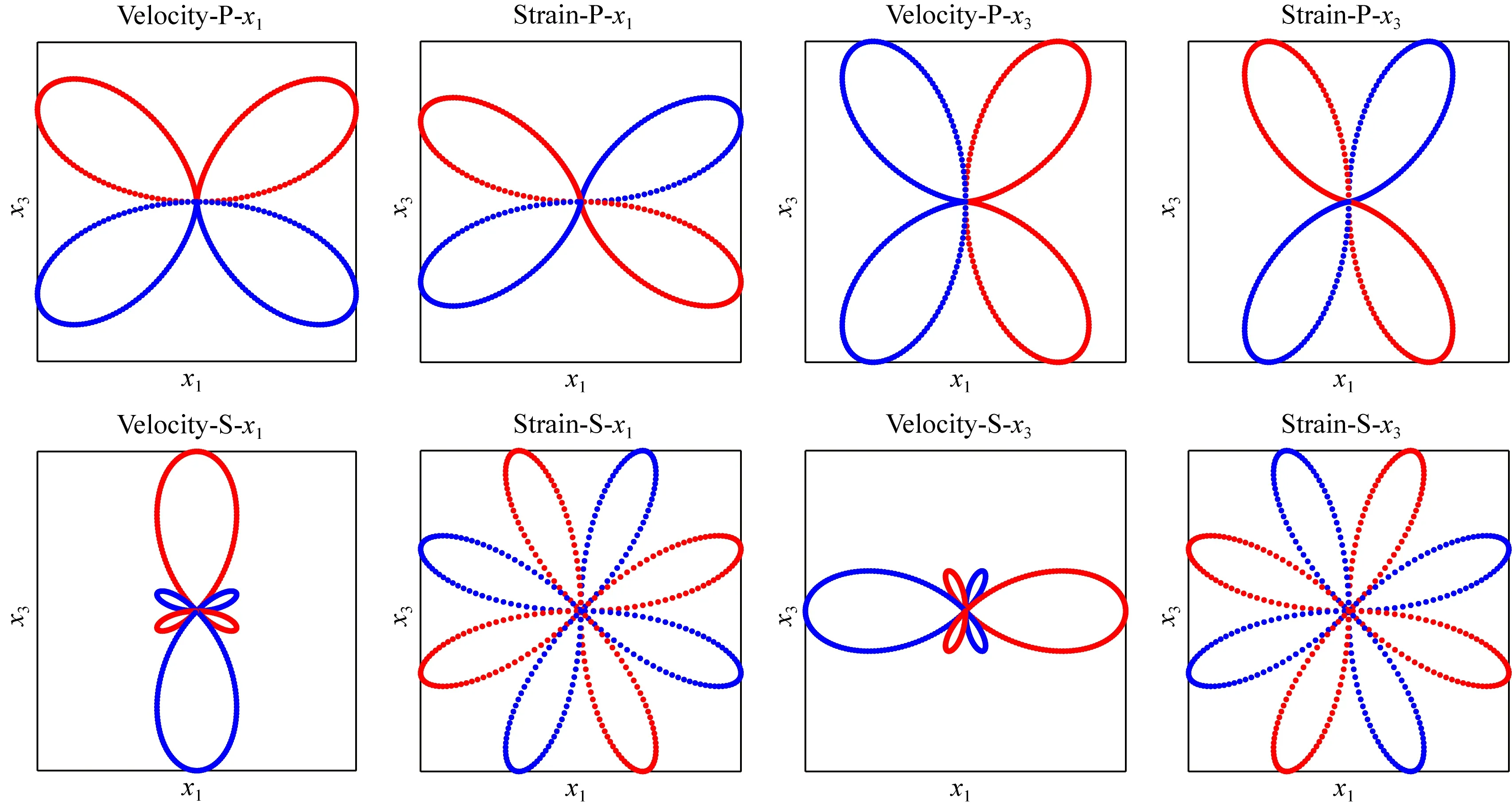
图5 DC震源在x1x3平面内x1和x3分量的速度辐射花样和应变辐射花样

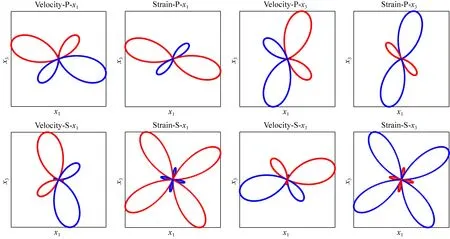
图6 逆冲断层震源在x1x3平面内x1和x3分量的速度辐射花样和应变辐射花样

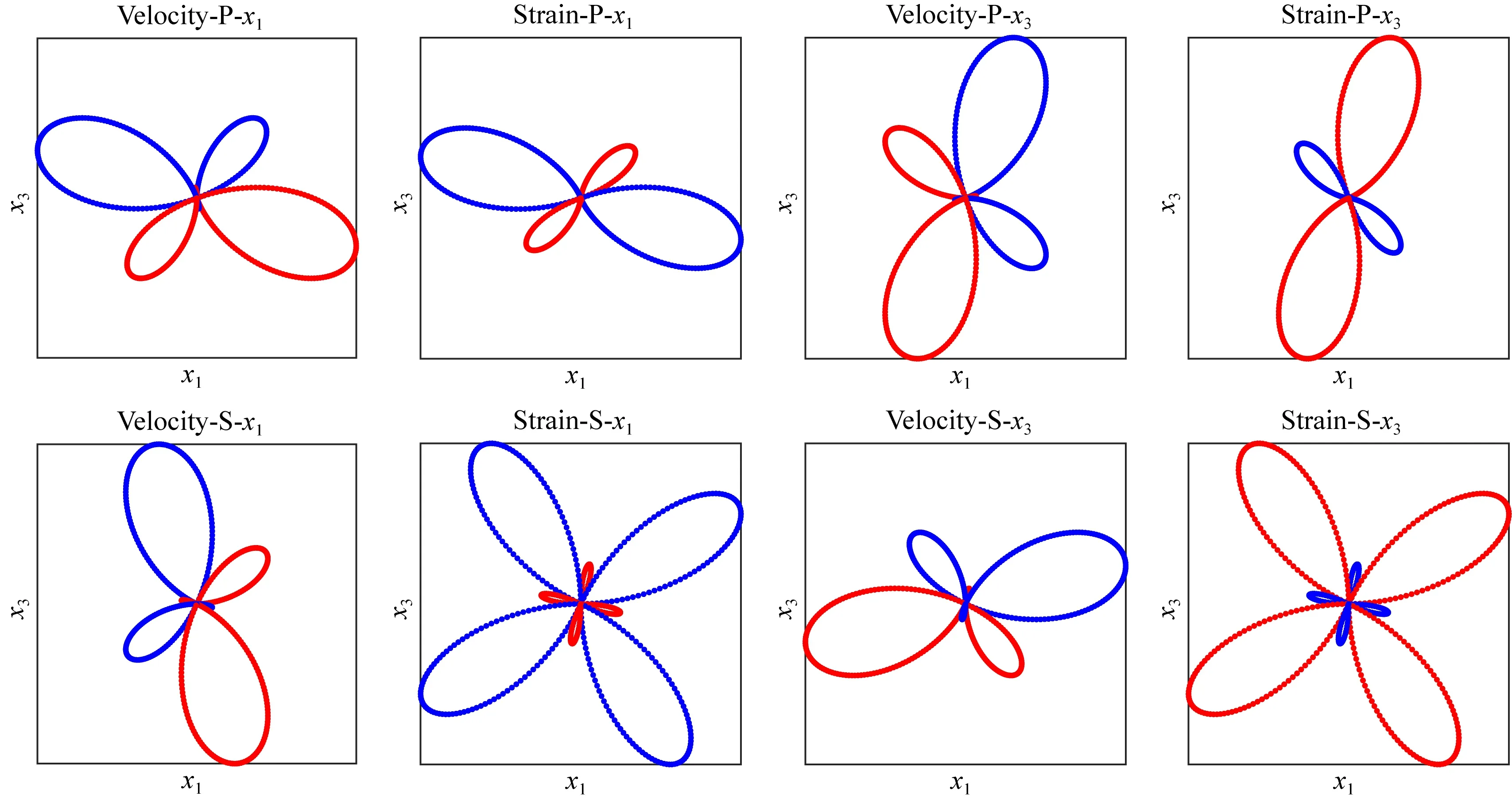
图7 正断层震源在x1x3平面内x1和x3分量的速度辐射花样和应变辐射花样

图8 一般位错震源在x1x3平面内x1和x3分量的速度辐射花样和应变辐射花样

图9 全矩张量震源在x1x3平面内x1和x3分量的速度辐射花样和应变辐射花样

表1 本文采用的震源模型

从辐射花样图中可以看出，无论是何种震源，P波的速度辐射花样与应变辐射花样形状上非常相似，但S波的速度辐射花样与应变辐射花样的差别较大，尤其是以DC成分为主的震源类型，可以看到这种震源的S波速度辐射花样分为6瓣，而在应变辐射花样中分为8瓣.这也证明了这些震源的DAS应变响应中，S波极性将会发生更多的反转.另外，无论是P波还是S波，其应变辐射花样的极性与速度辐射花样的极性是对称相反的.考虑x1分量极性变化，如果速度的辐射花样两端极性相反，那么应变辐射花样的两端极性是一致的，反过来说如果速度的辐射花样两端极性相同，那么应变辐射花样的两端极性是相反的.这些现象在后续的理论合成记录中也能够得到佐证.同样的，x3分量的极性变化也是如此，在这里将不再赘述.

3 分布式光纤声波传感微振动数值模拟方法

分布式光纤能记录到轴向方向上的应变，根据应变与位移的关系式：

(24)

将位移数据投影到光纤上，计算沿光纤轴向的空间导数，可将位移数据投影到光纤上得到合成应变数据，但这并不是实际DAS测量获得的应变.DAS获得的是沿光纤轴向有限长度内的平均应变，这个有限长度也被称为标准距离(标距，gauge length).DAS应变可以用公式(25)来描述：

(25)

其中L是标距.标距的大小对DAS测量性能影响较大，标距越小，DAS空间分辨率越高，但信噪比较低；标距越大，DAS空间分辨率越低，但信噪比较高(Dean et al.,2017; Hartog, 2017).一般来说，标距需要在测量距离、空间分辨率和信噪比中寻找平衡.

公式(25)提供了计算DAS应变的一种方法.此外，还可以利用光纤的瑞利散射干涉模型，将光纤上每点的应变转化为瑞利散射光的相位，模拟真实的瑞利散射光信号，然后通过解调后向瑞利散射光信号，获得真实DAS应变响应(方欣栋，2018；马国旗等，2020).

4 数值算例

为了研究不同震源机制以及不同布设条件的分布式光纤微振动响应特征，本文建立了如图10所示的数值模型，该模型对应的观测系统有7条地面光纤测线，前6条光纤的长度均为2000 m，第7条测线(方形测线)的长度为4000 m，此外还有一条井中光纤测线8，其长度为1200 m.DAS系统参数设计如下：空间采样间隔为0.1 m，标距为1 m.震源位于地表以下200 m处，介质的纵波速度为3000 m·s-1, 横波速度为1731 m·s-1.采用表1设计的8种震源，使用50 Hz的雷克子波作为震源函数，根据上述理论模拟方法，可以获得各种情况下的合成数据.

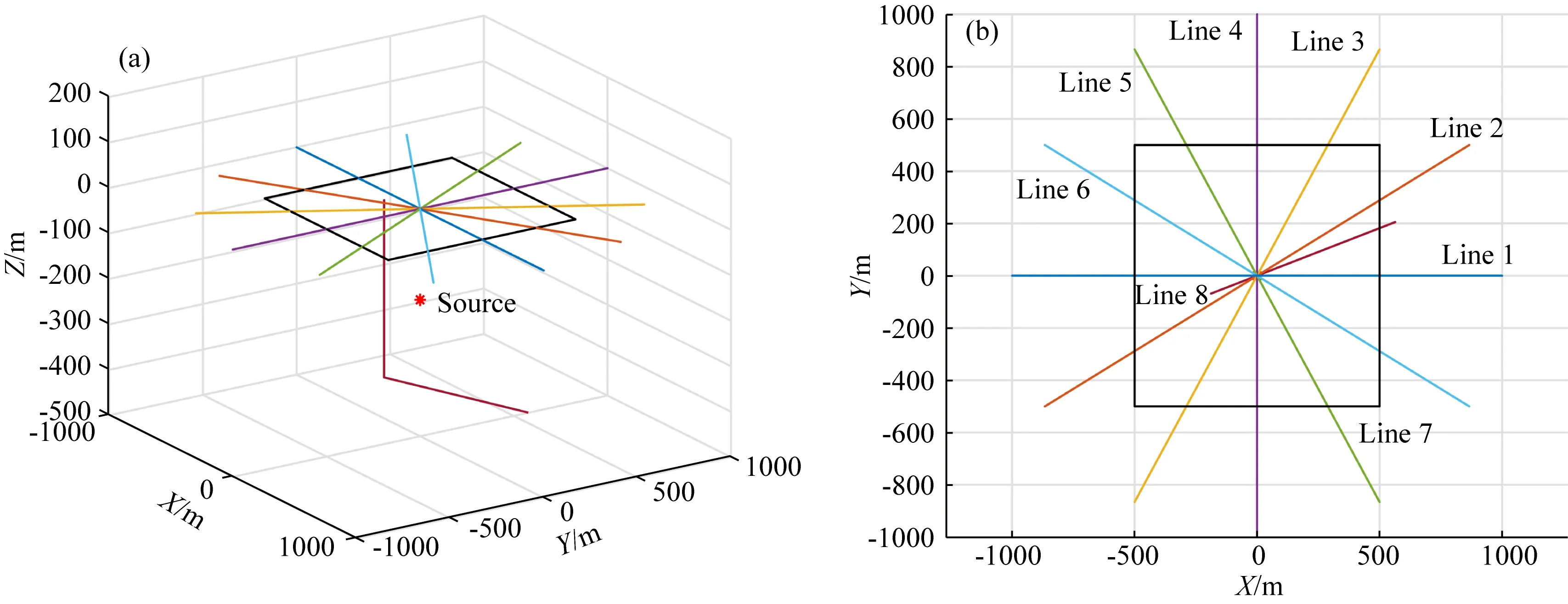
图10 (a)DAS观测系统，地面有7条测线，井中有一条测线.(b)观测系统的俯视图，地面测线按照逆时针顺序标记为Line 1—Line 6，方形测线标记为Line 7，井中测线标记为Line 8

图11是单力源的速度记录和DAS应变响应.图12是ISO震源的速度记录和DAS应变响应.由于ISO震源是一种对称源，且震源处在测线的中心，因此6条地面测线的观测记录是一样的.图13是CLVD震源的速度记录与DAS应变响应.本文采用的CLVD震源相对于水平面来说是对称的，因此6条地面测线获得的记录也是一样的.对比图11至图13的速度记录和DAS应变响应，可以看到速度记录有极性反转现象，而DAS应变响应没有极性反转现象.

图11 单力源的速度记录(左列)和DAS应变响应(右列)；从上至下分别代表测线1—6的记录

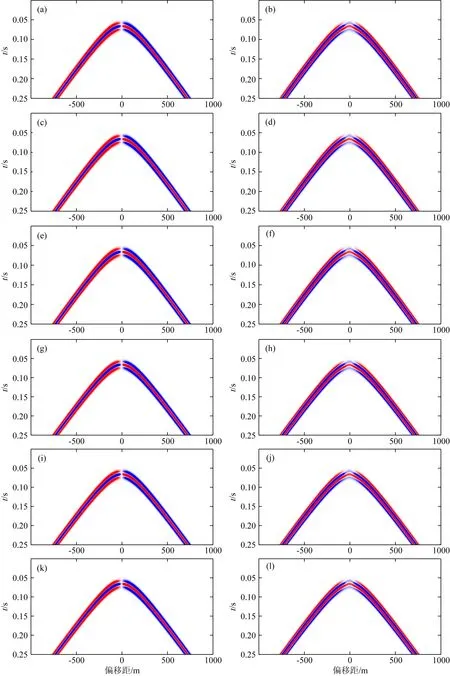
图12 ISO震源的速度记录(左列)和DAS应变响应(右列)；从上至下分别代表测线1—6的记录

图14是DC震源的速度记录与DAS应变响应，DC震源的DAS应变响应特征与测线布设方式有一定的相关性，例如测线4记录不到信号，而测线1、2、3记录的信号是相似的.与图11至图13观察到的现象不同，图14的DAS应变响应存在较多的极性反转现象.图15、图16和图17分别是逆冲断层震源、正断层震源与一般位错震源的速度记录与DAS应变响应，相较于DC震源的模拟结果，测线4可以记录到信号，但其他测线DAS应变响应的极性反转位置发生了变化.

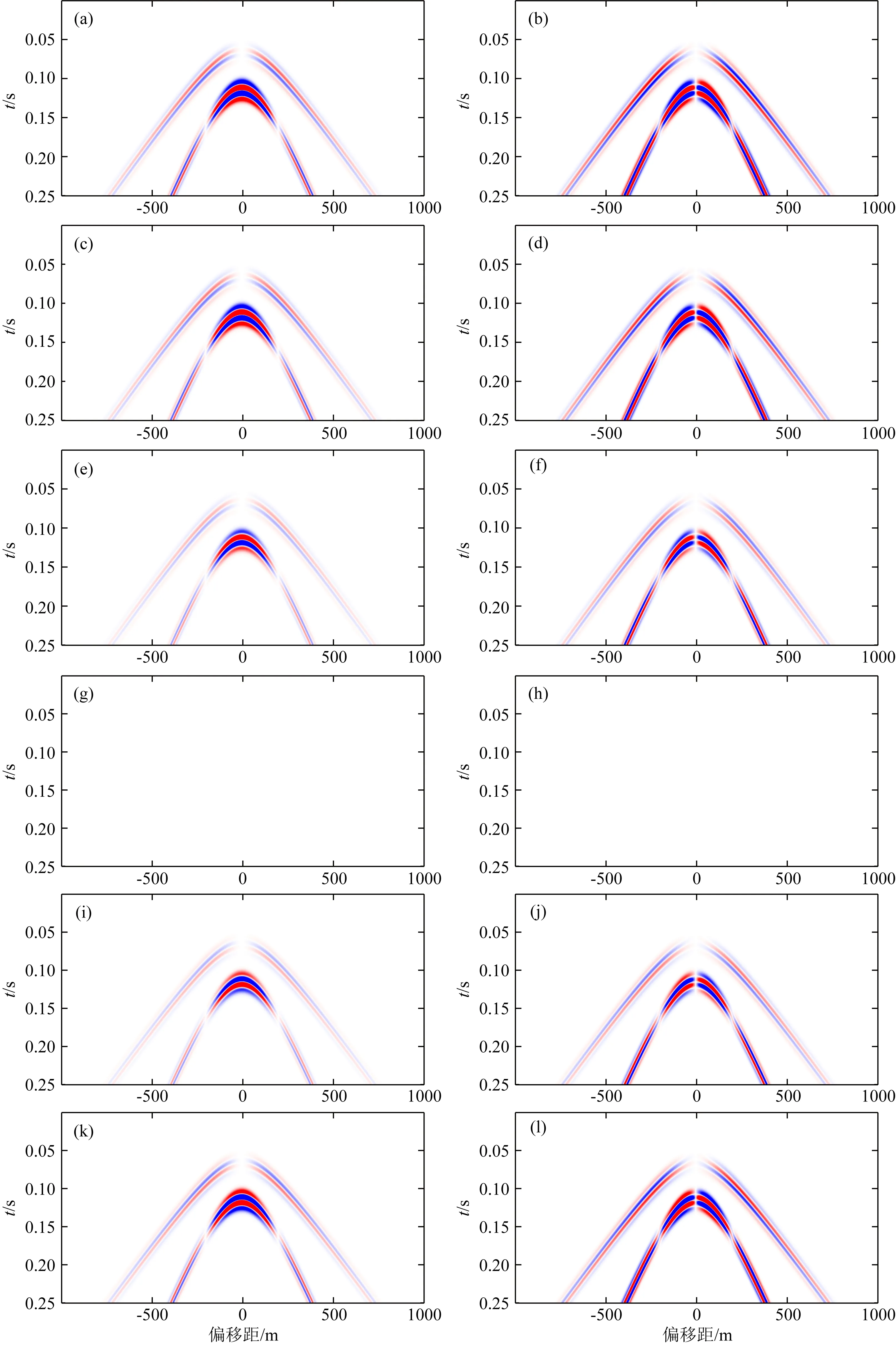
图14 DC震源的速度记录(左列)和DAS应变响应(右列)；从上至下分别代表测线1—6的记录

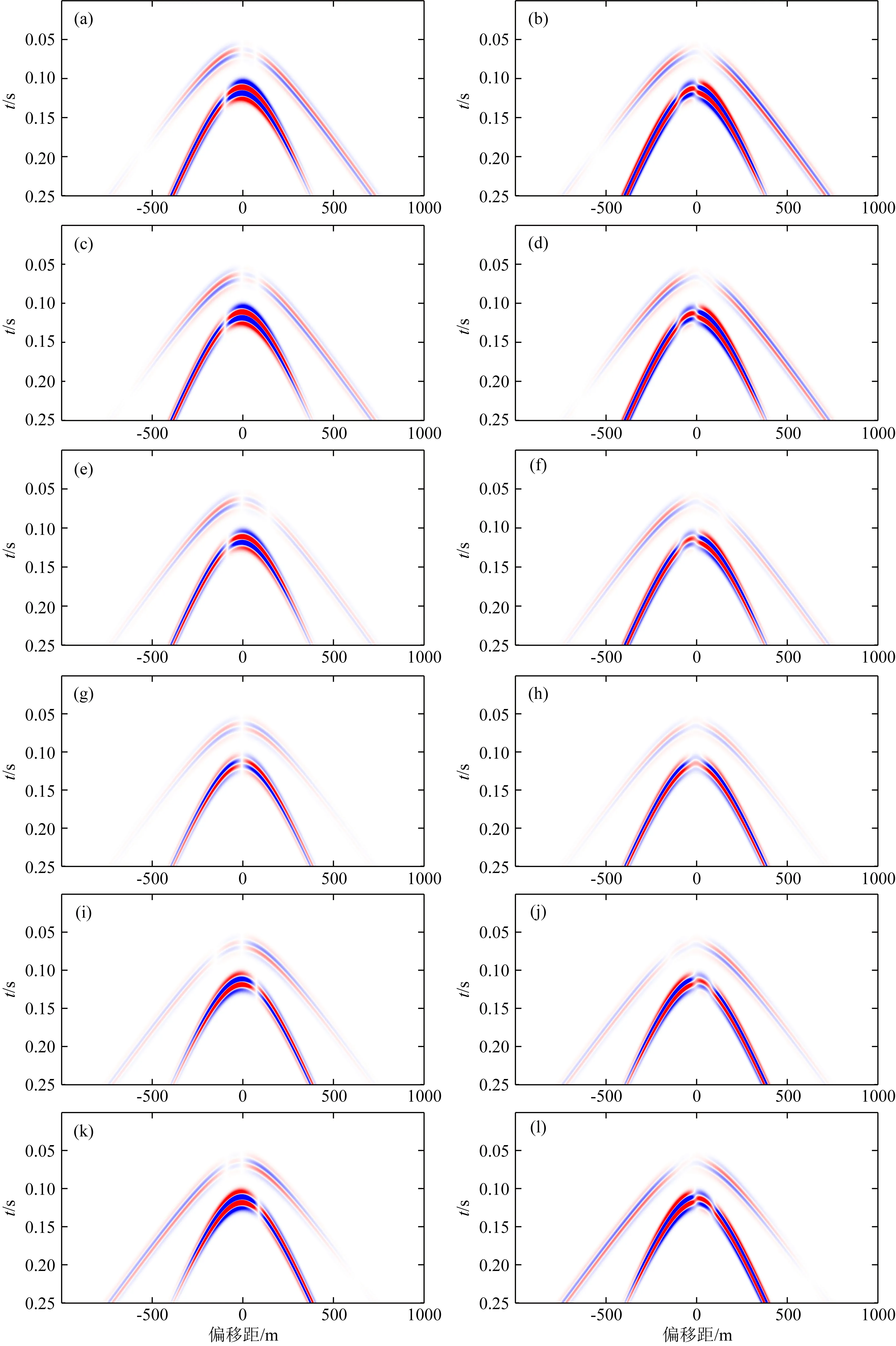
图15 逆冲断层震源的速度记录(左列)和DAS应变响应(右列)；从上至下分别代表测线1—6的记录

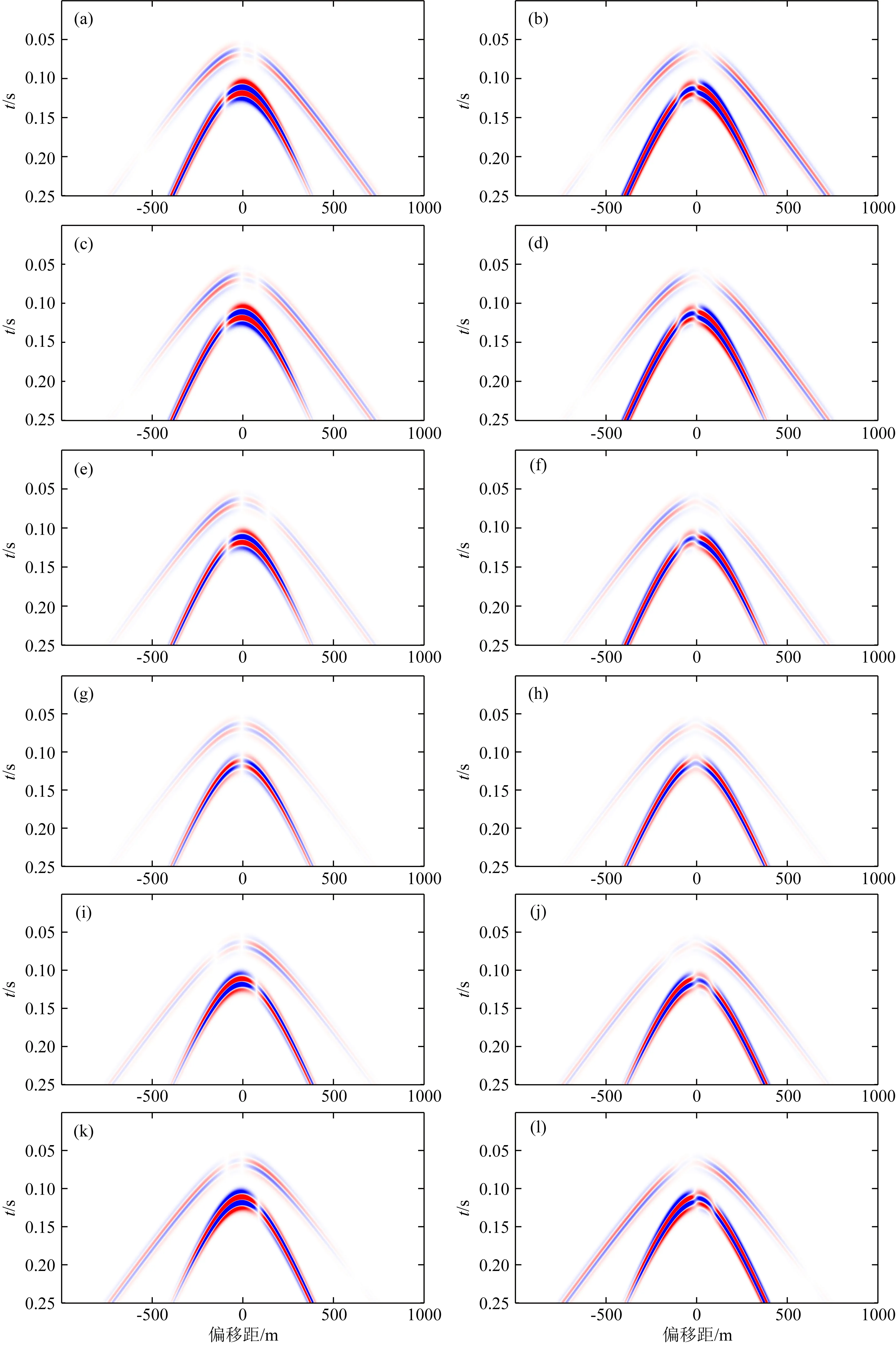
图16 正断层震源的速度记录(左列)和DAS应变响应(右列)；从上至下分别代表测线1—6的记录

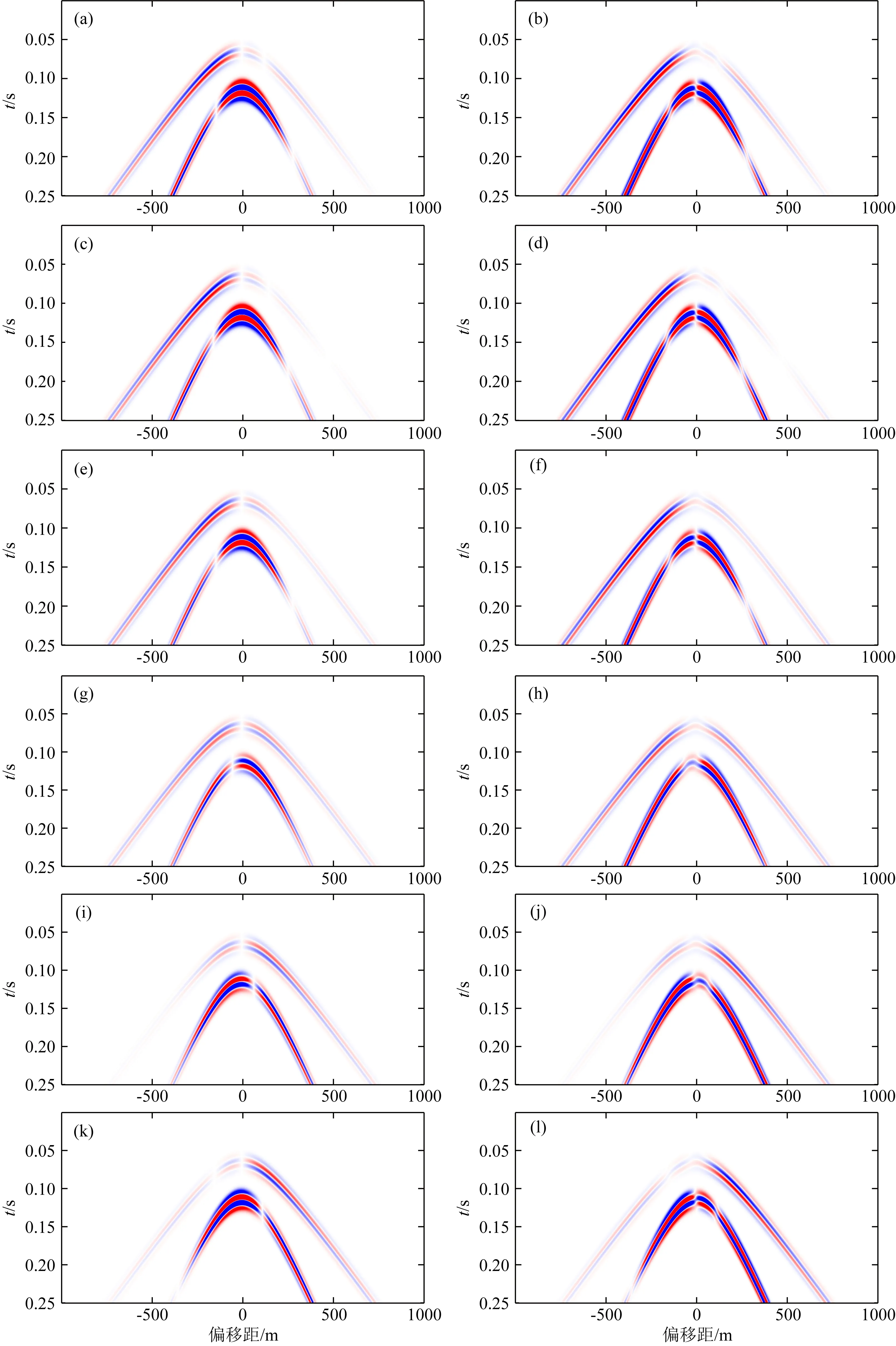
图17 一般位错震源的速度记录(左列)和DAS应变响应(右列)；从上至下分别代表测线1—6的记录

图18展示的是全矩张量震源的速度记录与DAS应变响应，综合图14至图18可以发现，含DC成分震源模型DAS应变响应具有更多的极性反转现象，例如图18中S波在测线1至测线4上产生的DAS应变响应具有三次极性反转现象，而在测线5和测线6上具有两次极性反转现象.

图18 全矩张量震源的速度记录(左列)和DAS应变响应(右列)；从上至下分别代表测线1—6的记录

图19是测线7接收到的8种震源的速度记录与DAS应变响应.由于该测线是方形的，属于二维测线，图19中的横坐标不再是偏移距而是光纤长度，可以看到每张图中都会有4个同相轴.图20是测线8接收到的8种震源的速度记录与DAS应变响应.为了模拟水平井光纤数据采集情况，将光纤的布设方式设计为L型，记录到的信号分为垂直段和水平段.对比图11至图20，可以发现相同震源的速度记录与应变响应是相似的.

图19 测线7对应的8种震源的速度记录和DAS应变响应；按照由上而下，从左到右的顺序，8种震源分别是：单力源(a, b)、ISO震源(c, d)、CLVD震源(e, f)、DC震源(g, h)、逆断层震源(i, j)、正断层震源(k, l)、一般位错震源(m, n)、全矩张量震源(o, p)

图20 测线8对应的8种震源模型的速度记录和DAS应变响应；按照由上而下，从左到右的顺序，8种震源分别是：单力源(a, b)、ISO震源(c, d)、CLVD震源(e, f)、DC震源(g, h)、逆断层震源(i, j)、正断层震源(k, l)、一般位错震源(m, n)、全矩张量震源(o, p)

5 结论

本文研究了不同震源机制、不同布设方式的DAS应变响应特征，主要结论有以下几点：

(1)应变辐射花样与速度辐射花样有区别.从形态上来说，各种震源机制下P波的速度辐射花样和应变辐射花样形状较为相近，S波在含DC成分震源机制条件下两者的形态上差别明显.以震源所在位置的垂向方向或水平向方向作为对称轴，如果速度辐射花样两端的极性是相同或相反，那么相对应的应变辐射花样两端极性就是相反或相同.

(2)理论合成记录结果表明含DC成分震源的S波DAS响应相较于检波器记录，存在更多的极性反转现象，且多出的极性反转一般发生在零偏移距处.

(3)ISO、CLVD震源由于震源自身的对称性，其应变响应与光纤的布设方式没有关系；而含DC成分震源在不同布设测线上的DAS响应变化不同，比如纯DC震源在某些测线方向可能接收不到任何响应，体现了DAS对方向的敏感性.

本文研究的是各向同性均匀介质情况下的DAS响应特征，但真实地下介质情况非常复杂，需要进一步研究各向异性非均匀介质中的DAS响应特征.