利用区域地震记录测定地震辐射能量
2023-02-11王子博刘瑞丰李赞孔韩东胡岩松
王子博,刘瑞丰,李赞,孔韩东,胡岩松
中国地震局地球物理研究所,北京 100081
0 引言
地震辐射能量作为描述震源动态特征的物理量,可以帮助我们理解地震破裂的物理过程、断裂带的演化和强震的产生机制等(Kikuchi, 1992; Venkataraman and Kanamori, 2004; Picozzi et al., 2019).随着全球宽频带数字台网的迅速发展,大量高信噪比的地震数据资料显著提高了地震辐射能量的测量精度.目前,已经发展出多种测定地震辐射能量的方法(Boatwright and Choy, 1986; Choy and Boatwright, 1995; Newman and Okal, 1998; Izutani and Kanamori, 2001; Di Giacomo et al., 2008; Convers and Newman, 2011).其中为了实现快速测定的目的,前人研究多使用远震体波(35°≤Δ<80°)测定地震辐射能量,受到全球地震台站分布不均和波形记录质量的限制,一般只能在部分地区产出MW≥6.0地震的辐射能量,对于某些缺乏高质量地震记录的地区发生的地震则需要MW≥6.5.相比较而言,地震矩M0作为描述震源静态特征的物理量,测定时可以联合使用近震资料和远震资料得到稳定结果,目前各个机构普遍将MW≥5.0地震的地震矩作为日常产出数据.因此,利用区域地震记录(5°≤Δ<35°)测定地震辐射能量具有较大优势.首先,与远震记录相比,利用区域地震记录可以在地震发生后更快测定结果,为地震应急和灾害评估提供及时参考;其次,对于中等规模(5.0≤MW<6.0)的地震,部分远震记录信噪比较低,仅使用远震记录有时很难得到稳定可靠的结果,这就限制了测定部分地震辐射能量的震级下限.相比较而言,区域地震记录较多且波形质量较好,可以解决由于远震记录不足或信噪比较低时中等规模地震的辐射能量较难测定的问题.
但存在以下问题使得利用区域地震记录测定的地震辐射能量与实际存在偏差:第一,测定地震辐射能量时需要考虑地震波的传播效应,包括双力偶模型在空间中产生的辐射花样系数、几何扩展项、非弹性衰减效应、深度反射折射波对地震记录的贡献和接收函数的影响,其中主要影响因素为几何扩展项和对非弹性衰减效应的校正(Okal, 1992; Venkataraman and Kanamori, 2004).几何扩展项g(Δ)即通过径向不均匀地球的传播效应,可以通过对Jeffreys-Bullen走时表平滑后直接微分的方法计算(Newman and Okal, 1998).由于Jeffreys-Bullen走时曲线没有考虑地幔转换带间断面处的不连续性,导致将该方法拓展到区域地震记录时,410 km和660 km间断面的存在会使得走时曲线出现偏折,这时使用原始Jeffreys-Bullen走时曲线的简单数值微分结果可能导致g(Δ)震荡并出现极值(Ebeling and Okal, 2012);第二,计算地震辐射能量时一般使用全球一维平均地球模型估计地球介质对地震波的衰减效应.随着震中距的降低,地球介质的各向异性效应影响逐渐明显,导致平均地球模型与实际情况差距增大,这时仅考虑平均地球模型可能不能满足要求.
为了将区域地震记录应用于快速测定地震辐射能量的工作中,本文从地震辐射能量的测定原理出发,通过引入区域辐射能量校正系数,发展了一种利用区域地震记录快速测定地震辐射能量的方法.随后,使用全球地震台网和区域地震台网提供的宽频带记录研究了2009—2021年发生在中国大陆的MW≥5.0地震事件,并对结果进行分析比较.最后,结合地震矩资料,讨论了中国大陆地震的能矩比统计特征.
1 理论和方法
地震发生后,震源释放的地震波传播到台站时会受到地球介质衰减作用的影响,所以对于台站记录必须进行修正,恢复地震波在传播过程中损耗的能量,才能得到地震波的总能量.如果地球上的地震台站分布均匀且密集,就可以利用这些修正后的台站记录确定能量通量,将能量通量相加得到总辐射能量.但地球上的台站数量有限且分布不均匀,观测数据一般只覆盖震源球的一部分,因此在实际处理中可以根据这次地震的震源机制解计算每个台站的辐射花样系数,通过移除这些台站对应的辐射花样系数,将数据反向投影到整个震源球上得到这次地震的辐射能量.根据单个台站确定地震辐射能量的方法叫做单台地震辐射能量测定法.其基本原理的简单数学描述如下:
假设地震发生在无限大、不衰减的介质中,震源以地震波的形式传播到远场的能量称为地震辐射能量.Haskell(1964)提出地震辐射能量ER的理论计算公式为
(1)
(2)
其中P波球面平均辐射花样系数平方〈FP〉2=4/15,FgP为P波组(P,pP和sP波)的广义辐射花样系数,作用是根据震源机制解校正不同震中距和方位角上的台站对应的辐射花样系数,ε*为P波组能量通量,计算公式为
(3)
其中ω为频率,u(ω)为不同频率对应的速度谱,t*(ω)为非弹性衰减因子,等于震相走时与介质Q值的比,RP=a/g(Δ),其中a为地球半径,g(Δ)为几何扩展项(Newman and Okal, 1998).几何扩展项g(Δ)反映了地球径向的不均匀性,即地震波从震源到达接收台站后不再具有球面对称性,其结果可以通过对Jeffreys-Bullen走时表求微分得到(Okal, 1992).如图1所示,当Δ>35°时,g(Δ)随着震中距平稳变化且对震源深度变化不敏感;当15°≤Δ<35°时, 由于Jeffreys-Bullen地球模型没有考虑地幔间断面的存在,导致震中距在15°~25°附近的结果受到410 km间断面影响,震中距在20°~30°附近的结果受到660 km间断面的影响,震中距在15°、20°和25°左右时g(Δ)出现极值,所以在这个震中距范围内的g(Δ)结果不可靠(Newman and Okal, 1998).当震中距小于15°时,浅层地壳不均匀性随着震中距的减小而增大,对于测定辐射能量的主要影响变为一维平均地球模型模拟地下介质对地震波的非弹性衰减效应与实际衰减的偏差,即对能量通量项ε*的影响.
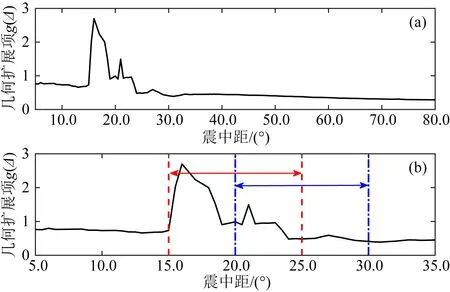
图1 基于Jeffreys-Bullen走时表计算的几何扩展项g(Δ)(a)本研究中使用的震中距范围(5°<Δ<80°),(b)区域地震记录(5°<Δ<35°),红色虚线和蓝色虚线分别代表410 km和660 km间断面造成的影响
为了解决这个问题,我们提出了区域辐射能量校正系数r(Δ):
(4)

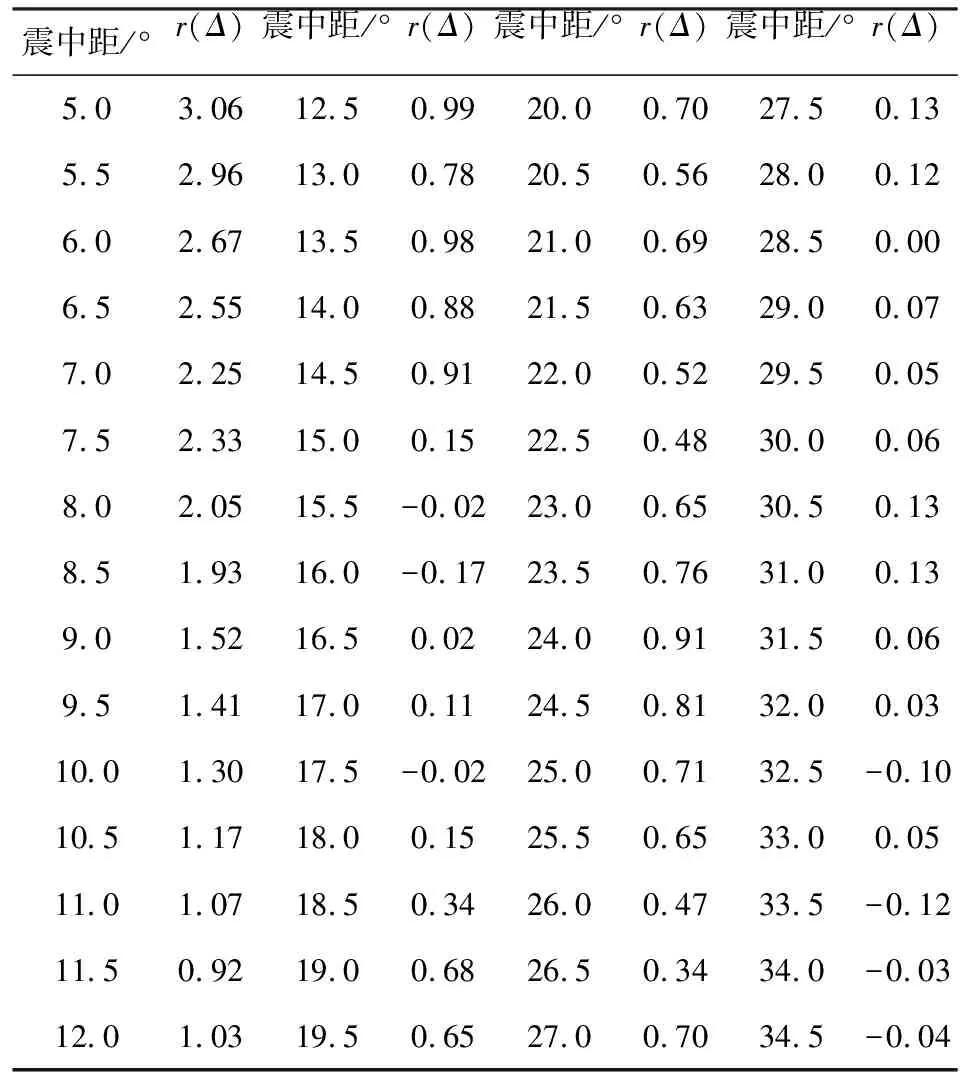
表1 震中距对应的区域辐射能量校正系数
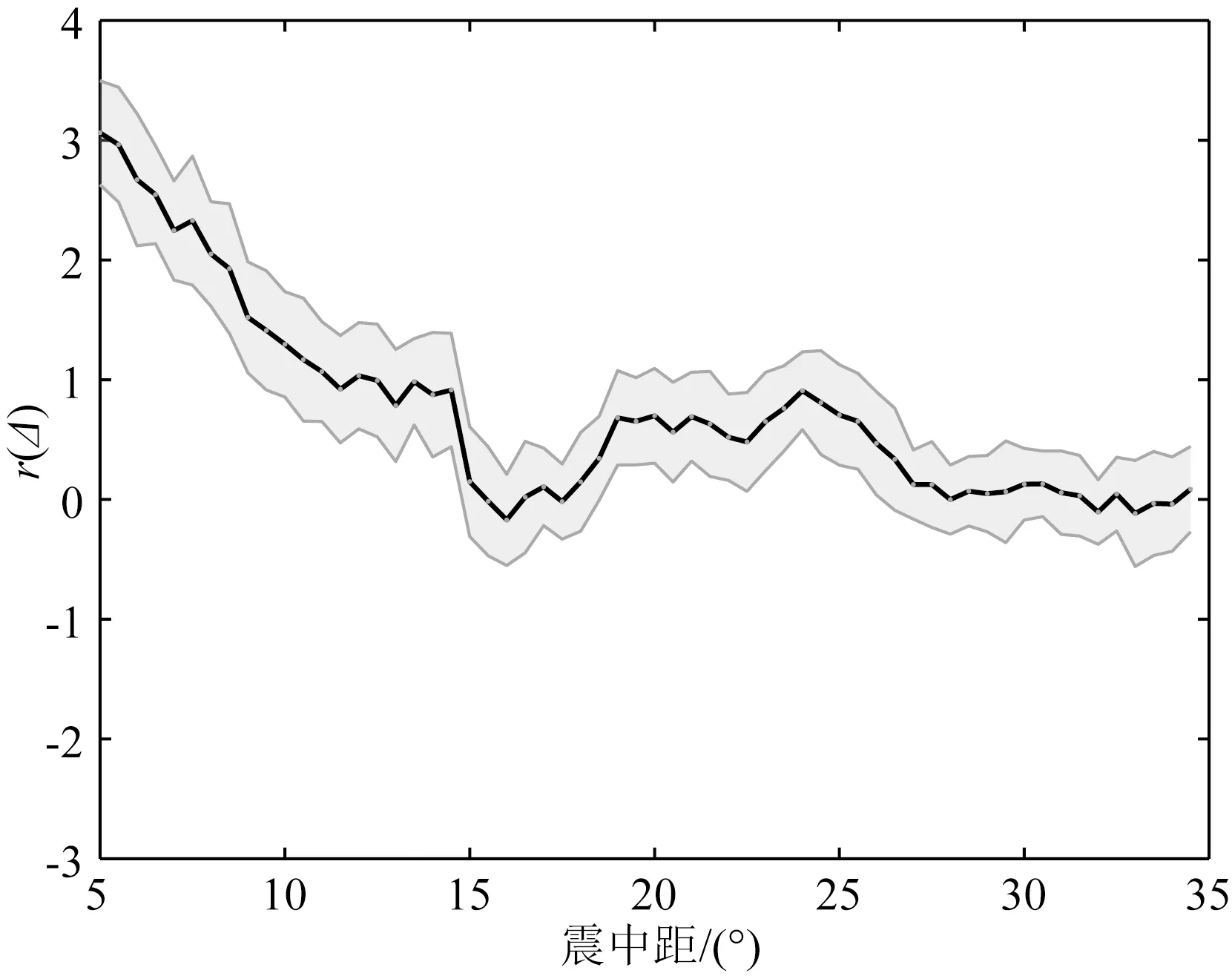
图2 区域辐射能量校正系数值随震中距的变化关系(灰色区域为±1个标准差范围)
该方法的原理可以解释为:当震源与台站间的距离在15°~35°时,造成地震辐射能量出现偏差的主要影响因素为几何扩展项g(Δ),几何扩展项的结果只与震源和台站的相对位置有关,与震源机制解、能量通量等因素无关,对辐射能量的影响是线性的,这时得到的r(Δ)代表了对走时表连续采样计算的几何扩展项与实际的平均偏差;当震中距小于15°时,选择固定时间窗和积分频段避免了波形因素对结果的影响后,r(Δ)代表了理论衰减与实际衰减间的平均偏差.由于震源和我们使用的大部分台站位置都处于大陆,地下介质的各向异性变化较大,利用小于5°的台站得到的计算结果偏差过大,因此我们将最小震中距设定为5°(Burdick, 1981).在这个区间内,通过每个震中距区间不同方位角的大量台站测定结果与远震结果比值的平均值作为校正系数,可以显著降低由于理论衰减和实际衰减的差异造成的偏差.
通过引入区域辐射能量校正系数,P波辐射能量的计算公式变为
(5)
一般仅通过计算P波或S波辐射能量确定地震辐射能量,P波与S波能量的关系为
如图10所示,当正向及反向分别加载至CD和C′D′段卸载时,卸载路线分别沿56和5′6′进行,卸载刚度分别取K56和K5′6′;采用拟合法对卸载点56和5′6′之间的所有实测数据进行拟合,分别得到正向加载CD和反向加载C′D′段所有数据点的卸载刚度K56和K5′6′;然后再对各阶段所有卸载刚度进行无量纲化处理并采用幂函数进行非线性回归拟合,分别得到K56/K0与+Δ5/(+Δm)及K5′6′/K0′与Δ5′/(-Δm)之间的非线性关系曲线,如图13所示。
(6)
对于双力偶源,S-P波能量比q=15.6(Boatwright and Choy, 1986).综上所述,可以得到基于区域地震记录的单台地震辐射能量测定公式:
5°≤Δ<35°.
(7)
2 测定结果分析
2.1 辐射能量结果分析
基于上述方法和步骤,我们计算了2009—2021年发生在中国大陆的66次地震的辐射能量,震中分布如图3所示,地震参数如表2所示,矩震级MW范围5.1~7.4,其中:5.1~5.9级地震46次,6.0~6.9级地震19次,7.0级以上地震1次,震源深度为6~28 km.为了方便比较,这里我们引入能量震级Me(Choy and Boatwright, 1995)描述地震辐射能量ER的大小:
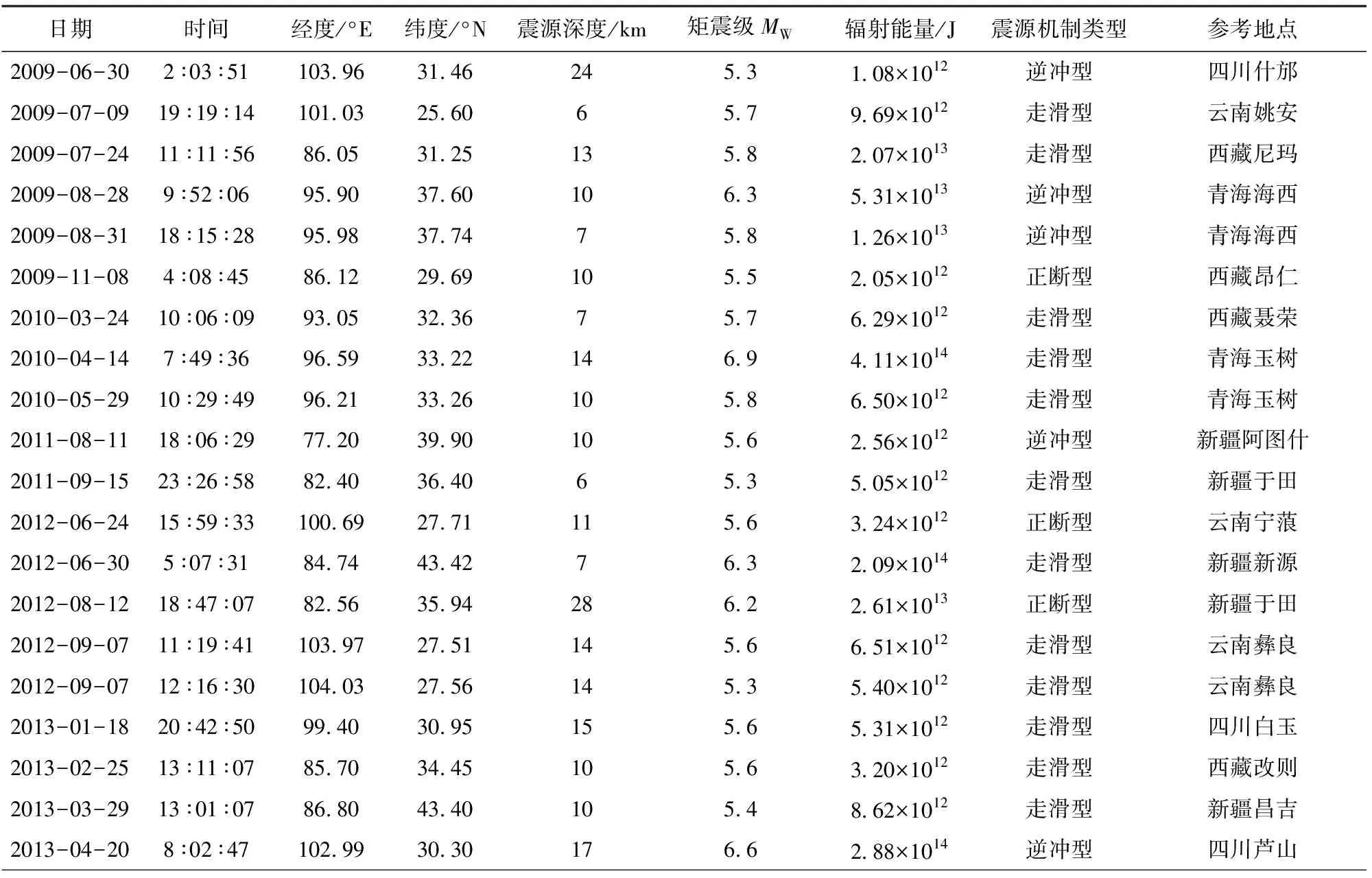
表2 地震的震源参数
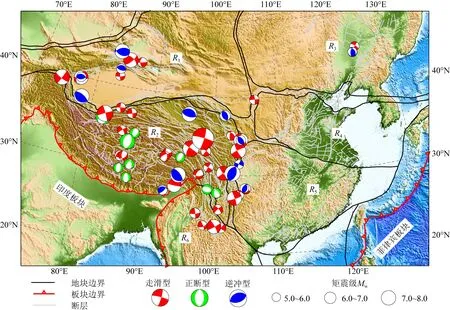
图3 地震震中分布图(断层和地块信息参考邓起东等(2003), 张国民等(2005))
Me=2/3(log10ER-4.4).
(8)
图4为校正前后单台能量震级差值在震中距上的分布图(a、c)和仅考虑区域地震记录时的单台偏差条形统计图(b、d).将校正前后的结果进行比较可知,校正前的单台结果明显偏高,偏差平均值为0.45,标准差为0.56;震中距小于28°的记录计算的结果与远震结果偏差较大,偏差平均值同样为0.45,而震中距大于28°的结果几乎没有偏差.相比较而言,校正后的单台偏差统计结果基本呈正态分布,其中偏差值≤±0.3的台站记录为3027条,占所有结果的74%.平均值为0,标准差为0.29.
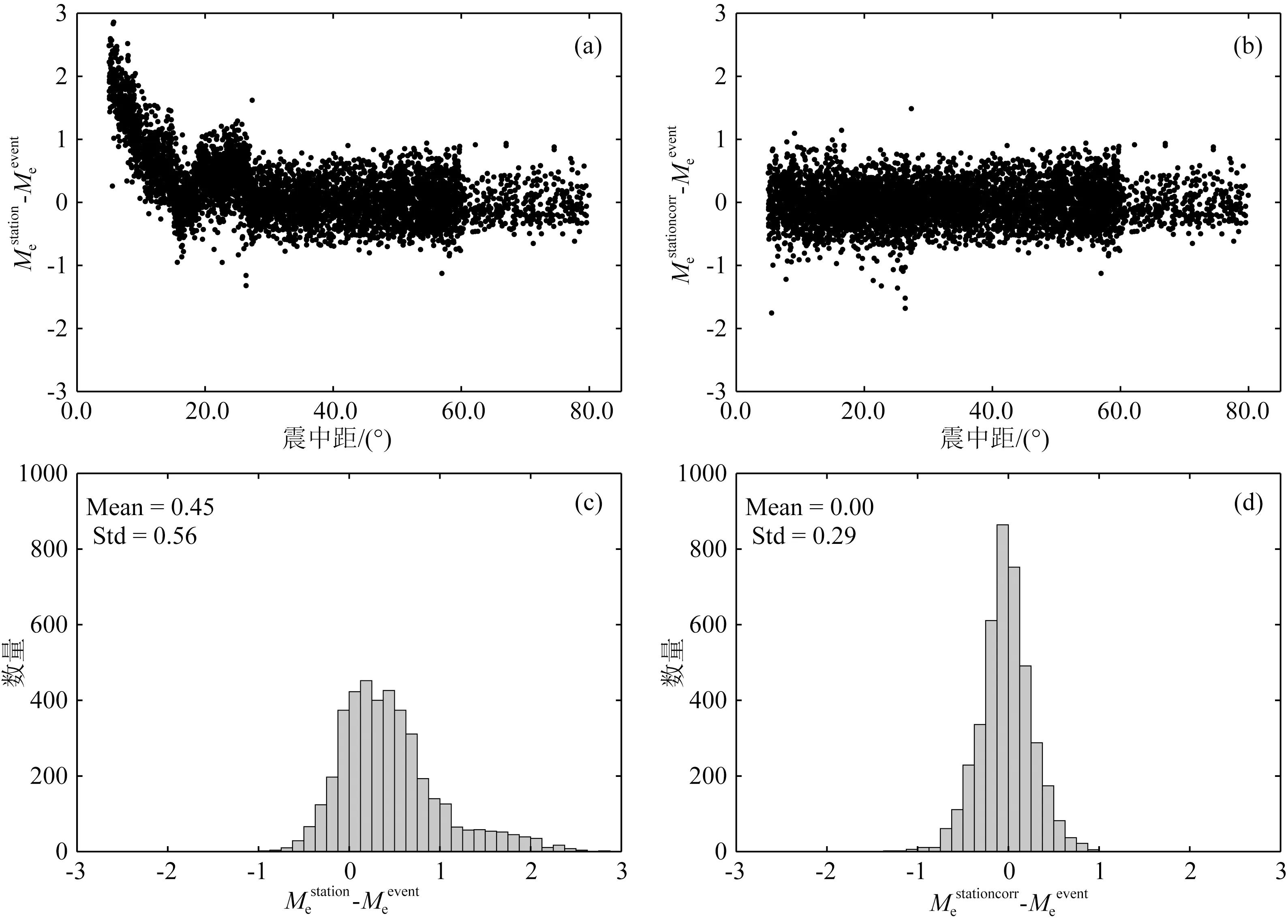
图4 单台和事件能量震级的偏差与震中距的关系和偏差统计直方图
在图5中将校正后的单台结果按方位角和震中距分类,统计了单台结果与事件的偏差关系.图5a是单台平均偏差在方位角上的分布.从图中可知,各个区间的结果偏差不大,除了0°~45°区间外,其他范围的偏差主要介于-0.1~0.1.不同方位角对应台站的计算结果存在差异的原因包括以下两点:第一是地下介质的横向不均匀性和地震破裂方向性的影响(Venkataraman et al., 2002).在远震范围内地震的破裂尺度与震中距相比较小,震源可近似为点源,且一维地球模型能够满足需要;随着震中距的降低,横向不均匀性和破裂方向性的影响逐渐增加.第二是震源机制解的影响.对于某些地震,其震源比较复杂,震源机制解可能与实际震源存在差异.以上影响可以通过选择震源处方位角均匀覆盖的台站记录显著降低.0°~45°区间上的台站偏差稍大的原因与这个范围内的台站数量较少有关,但对最终结果影响不大.图5b为单台平均偏差在震中距上的分布.从图中可以看出,不同震中距范围内的平均偏差均在-0.1~0.1之内,说明地震辐射能量的测定结果对震中距变化不敏感.
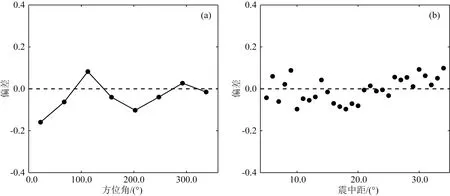
图5 不同(a)方位角和(b)震中距震级偏差的统计结果
(9)
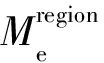
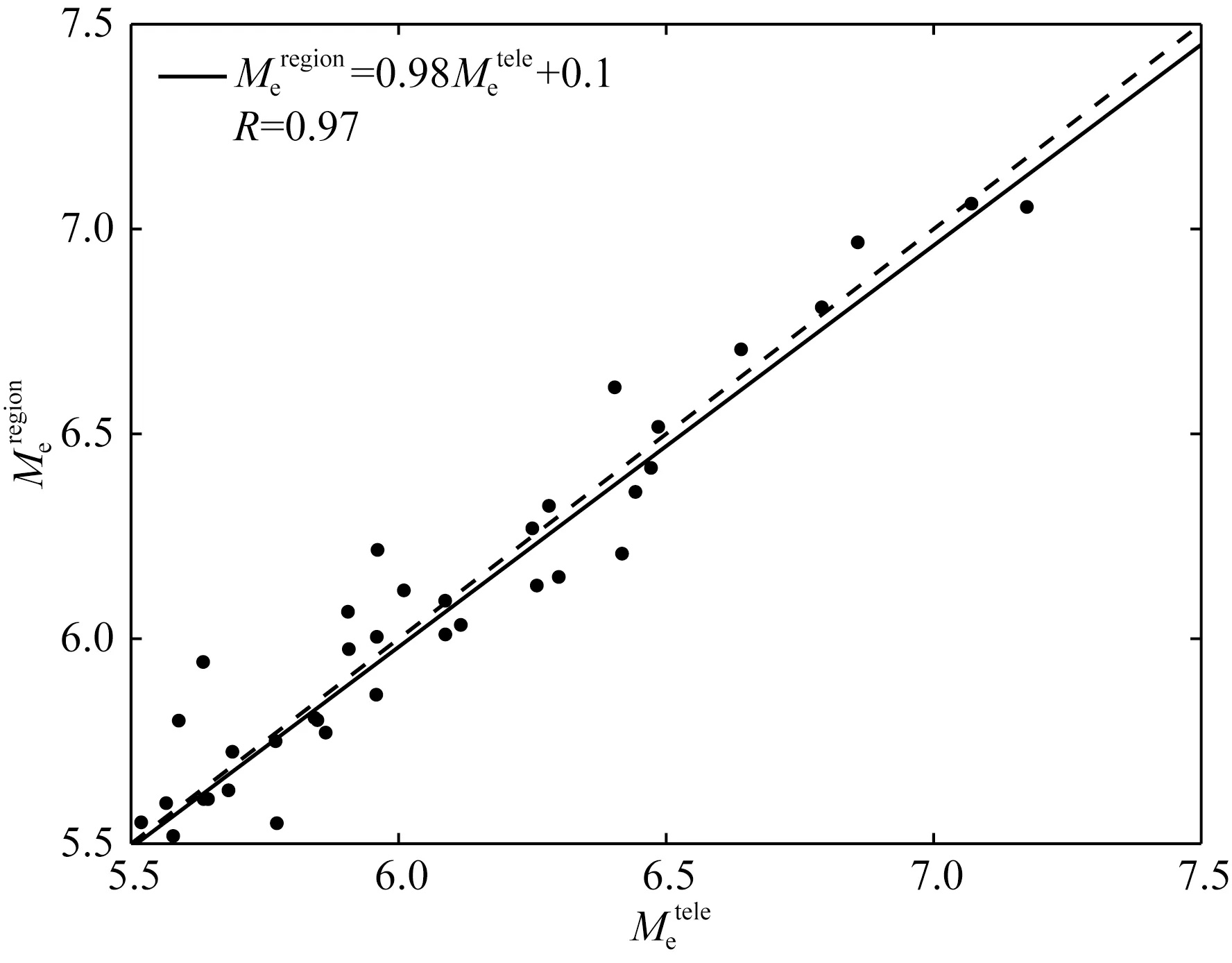
图6 远震能量震级(横坐标)与区域能量震级(纵坐标)的统计关系图
2.2 中国大陆能矩比分布研究
目前最广泛用于评估地震大小的震级为矩震级MW,矩震级MW是由地震矩M0导出的一个稳定且统一的衡量地震规模的标度(Hanks and Kanamori, 1979).地震矩M0描述了震源破裂前后的应力释放大小,与构造形变直接相关,但其仅描述了震源的静态特征,而地震辐射能量与破裂的复杂性密切相关,描述了地震破裂的动态过程(Husseini, 1977; Kanamori et al., 2020).因此,长期以来地震辐射能量与地震矩的比值(能矩比)一直是地震学家关注的主要问题,这个无量纲量与地震破裂所涉及的应变有关,直观地反映了震源破裂过程的动力学特征(Newman and Okal, 1998; Baltay et al., 2014; Okal, 2019).在这部分中我们对本研究涉及地震的能矩比特征进行了讨论.
结合GCMT提供的地震矩结果(图7)得到中国大陆地震的平均能矩比为2.4×10-5,与吴忠良等(2002)利用NEIC能量目录和GCMT地震矩目录得到的1987—1998年中国大陆地震的平均能矩比2.67×10-5基本一致.参考GCMT提供的震源机制解,按照Hauksson(1990)的定义将数据集中的地震分类,得到走滑型地震的平均能矩比为2.85×10-5,正断型地震的平均能矩比为9.03×10-6,逆冲型地震的平均能矩比为2.19×10-5;结果符合走滑型地震的能量释放效率高于倾滑型地震的特征(Choy and Boatwright, 1995).
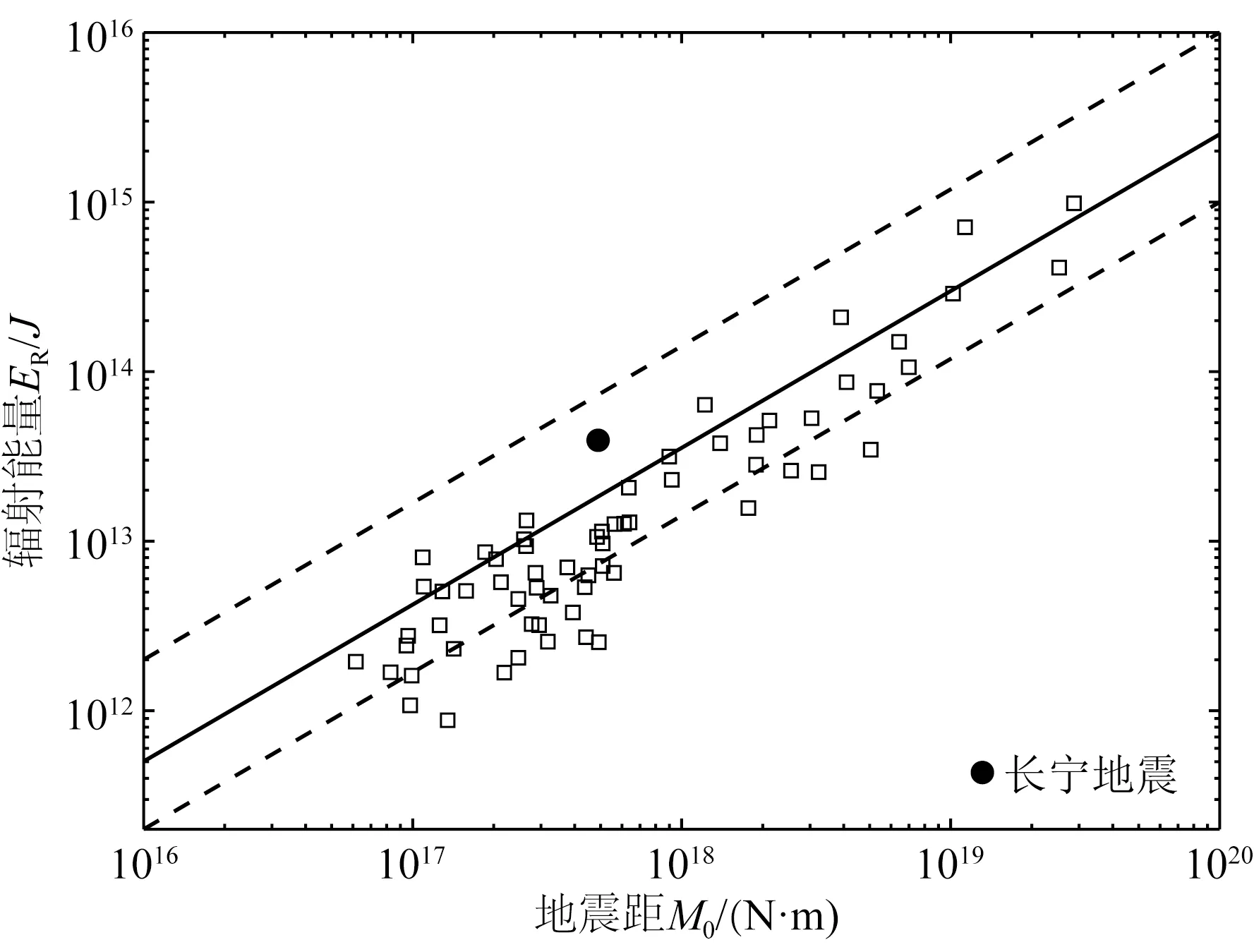
图7 中国大陆地震的辐射能量(ER)与地震矩(M0)对比图
为了探究能矩比的区域特征,在图8中将地震按所处地块划分后分析了地震区的整体特征.结果发现发生在西域地块西南部(红色区域)的地震能矩比整体偏高,为3.27×10-5;青藏地块东部(绿色区域)的地震能矩比与平均能矩比接近,为2.5×10-5;青藏地块西部(蓝色区域)的地震能矩比整体偏低,为1.26×10-5.区域平均能矩比特征体现了该地区的能量释放水平,可以作为衡量该地区应力积累情况的间接参数,较高的能矩比表明该地区的应力积累水平较高,未来发生高能矩比地震的可能性更大.
图8 对数能矩比的区域分布特征
同时可以看出,同一区域内的地震能矩比差异显著,能矩比的范围为5.2×10-6~8.1×10-5,且离散度较大.能矩比具有较大变化的原因与很多因素有关,首先能矩比大小反映了震源辐射地震波的能力,与断层的破裂速度有关.当断层破裂速度较快时,震源会辐射出大量高频能量;反之震源以地震波形式辐射的能量较少;其次一般认为走滑型地震的能矩比高于倾滑型地震,发震位置相近的两次具有不同震源机制的地震可能会存在较大的能矩比差异;最后,应力积累较强或新鲜破裂的断层上发生地震的能矩比一般要高于应力积累水平较低或未发生新鲜破裂的地震(Choy et al., 2006).同一区域内不同地震能矩比的差异反映了地震破裂过程的较大差异,对于单次地震而言其能矩比可能与区域统计结果存在较大偏差,这也体现了不同地区地质构造的差异性和应力环境变化的复杂性.

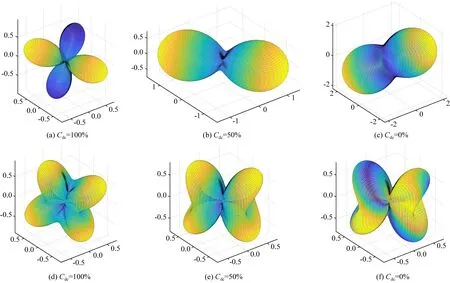
图9 震源中双力偶成分的比例对辐射花样系数的影响
(10)
其中RP、RS分别为P波和S波的辐射花样系数,VP、VS分别为P波和S波速度,ζ为P波与S波拐角频率的比值,最大值为VP/VS,最小值为1.因此辐射花样系数的变化会导致S-P波能量比发生显著变化,基于双力偶源假设得到的体波辐射花样系数和S-P波能量比将不再适用,得到的结果也会与实际存在明显差异.对于这次地震,震源的复杂性可能导致了地震辐射能量的测定结果存在偏差,进而对能矩比结果产生影响.
从上面的描述可知能矩比很好地反映了震源的物理特征,但其结果不利于实际应用和传播.在地震台网的日常产出中,通常使用震级描述地震大小,这时可以将M0和ER转化为矩震级MW和能量震级Me,能矩比关系就转化成能量震级Me与矩震级MW大小关系.对于Me大于MW的事件,与高能矩比事件类似,其能量释放高于预期,可能会造成更大的破坏;对于Me小于MW的事件,其造成的破坏可能低于预期.因此,当我们研究探讨震源的物理特征时,可以选择产出地震辐射能量和地震矩;如果出于公共传播的目的,将其转化为Me和MW更合适.利用两个震级之间的差异可以更快速地评估特定环境条件下与地震相关的危险及破坏程度.
3 结论
本文提出了一种利用宽频带垂直向区域地震记录(5°≤Δ<35°)快速测定地震辐射能量的方法,该方法通过建立与震中距相关的区域辐射能量校正系数,将地震辐射能量测定方法的适用范围拓展到了区域距离.利用该方法测定了中国大陆66次MW>5.0地震的辐射能量,并根据结果进行了分析和讨论.本文的主要研究结论如下:
(1)该方法可以使用区域地震记录测定MW≥5.0地震的辐射能量,降低了快速测定地震辐射能量方法的震级下限;对于MW≥5.5的地震,利用该方法测定的区域辐射能量与利用远震记录测定的结果具有较好一致性.
(2)中国大陆地震的能矩比范围为5.2×10-6~8.1×10-5,平均能矩比为2.4×10-5;能矩比大小与震源机制有关,走滑型地震的平均能矩比高于倾滑型地震.
(3)中国大陆能矩比整体分布存在区域特征,西域地块地震的平均能矩比高于青藏地块东部地震,青藏地块西部地震的平均能矩比最低,同一区域内的地震能矩比也存在差别,这表明不同断层上发生的地震能量释放过程存在明显差异.
致谢感谢两位审稿专家的建设性意见.本研究所使用的地震目录来自中国地震台网(CSN),波形数据下载自地震学联合研究会(Incorporated Research Institution for Seismology,IRIS)数据中心,震源机制解目录来自全球矩心矩张量(GCMT)项目.
