航磁水平分量数据的均衡滤波位场边缘增强研究
2023-02-11常畅郭华王海燕高锐韩松
常畅,郭华,王海燕,高锐,韩松
1 中国地质科学院地质研究所,北京 100037 2 中国地质大学(北京),北京 100083 3 中国自然资源航空物探遥感中心,北京 100083 4 中山大学地球科学和地质工程学院,广州 510275
0 引言
地球磁场是具有强度大小与方向的空间矢量,矢量磁测与传统的总场强度或梯度模量测量相比,可同时获取磁异常大小与方向信息,具有探测精度高、信息量丰富的特点,能够有效减少反演的多解性,获得更加精确的场源信息(林君等,2017).关于航空矢量磁测装备的研发与处理解释技术,国内外相继开展了相关的研究与应用(Hannaford and Haines,1974;Gee and Cande, 2002;Christense and Dransfield, 2002;闫辉等, 2010;孙昂等,2017;谢汝宽等,2017, 2021;Xie et al., 2020;杨力等,2020).我国于2017年在加格达奇地区首次实现航磁矢量测量飞行(谢汝宽等,2017),2018年在启鑫地区获取了高精度航磁三分量实测数据(Xie et al.,2020).
位场边缘识别在位场数据处理中具有十分重要的意义,能够充分发挥重磁数据探测范围广、横向分辨率高等优势,根据在密度或磁性存在差异的分界面具有重磁异常频率高和变化率大的特点,对断裂构造线或地质体边界线进行追踪识别,进而实现矿产资源构造勘察、地质填图和地热资源勘察等方面的作用.其中,导数类(Evjen,1936;Cordell, 1979;Nabighian,1972;Miller and Singh, 1994;Verduzco et al.,2004;Wijns et al.,2005;Wang et al.,2009;Ferreira et al.,2013;Cooper,2014)和数理统计类(杨高印,1995;Cooper and Cowan,2008;张凤旭等,2007;王彦国等,2013;Xu et al.,2015;段杰翔和徐亚,2020)的位场边缘识别方法应用较为广泛,随着图像处理技术的不断发展,图像增强类边缘识别方法也具有较多的研究与应用(Blakely and Simpson,1986;Zhang et al.,2005;赵希刚等,2008;Sertcelik et al.,2013).而传统的位场边缘识别方法主要被应用于磁总场异常ΔT,针对航磁矢量数据的位场边缘识别方法研究较少.对于航磁水平分量数据,在没有剩磁影响的情况下,北半球中高纬度地区,北向分量表现为南正北负,东向分量表现为东负西正,具有一定的方向特性(谢汝宽等,2021).因此,本文将广泛应用于图像处理领域(Daugman,1980, 1985, 1988;Jain and Farrokhnia, 1991;Mehrotra et al., 1992;Petkov, 1995;Petkov and Kruizinga, 1997;Hong et al., 1998;Greenberg et al., 2002;Yang et al., 2003)和地球物理数据处理领域(Sertcelik et al.,2013;Ji and Yan,2017)的Gabor滤波器的方向特性、尺度特性与航磁水平分量数据的方向特性进行了有效结合.
本研究利用提出的航磁水平分量数据的均衡滤波方法进行场源边界识别,该方法由Gabor滤波器和斜导数所构建,能够获得清晰、丰富的场源边界信息.为航磁矢量数据的处理与应用,提供了新的方法与思路,是对航磁矢量数据解释的有效补充.
1 方法原理
本文提出了新的基于航磁水平分量数据的边界增强方法.首先,分别对磁北向分量与东向分量应用多参数的Gabor滤波技术;然后,对两个分量的滤波结果进行组合增强;最后,应用斜导数方法对增强后的结果进行均衡,获得基于航磁水平分量均衡滤波的位场边缘识别结果.
二维的空间域Gabor滤波器是由一个具有一定频率和方向的正弦平面波组成,并被一个二维的高斯包络所调制,在图像增强技术中,通常使用滤波器中偶对称的实部进行计算,可以表示为(Jain and Farrokhnia, 1991; Hong et al., 1998; Yang et al., 2003; Sertcelik et al., 2013):
Rσx,σy,θ(x,y)=gσx,σy,θ(x,y)
(1)
其中,x′=xcosθ-ysinθ,y′=xsinθ+ycosθ,θ代表滤波器沿坐标轴逆时针旋转的角度,Gabor滤波器在θ方向具有低通滤波的作用,垂直于θ的方向具有带通滤波的作用.σx、σy分别为高斯函数沿x方向和y方向的标准差,通常假设σx=σy,λ为正弦平面波的波长,与传统的波长定义不同,这里指正弦平面波两个临近波峰的距离.
滤波器的核函数与参数σ、λ和θ有关,对于σx与σy的取值需要进行权衡,取值越大,对于噪声的抑制作用越明显,但滤波器越有可能产生虚假的波峰与波谷.同时,取值越小,滤波器越不会产生虚假的波峰与波谷,但去噪的效果不明显;波长λ的取值并不是独立的,与σx、σy具有一定的关联性(Petkov and Kruizinga, 1997);滤波器的方向取值与异常形态的方向有关.
Gabor的滤波输出是通过输入信号与Gabor核函数的卷积得到的.航磁水平分量数据的Gabor滤波公式可以表示为:
GX=Bx*gσx,σy,θ(x,y)
(2)
GY=By*gσx,σy,θ(x,y)
(3)
其中,Bx为北向分量,By为东向分量,g(x-a,y-b)为Gabor滤波器核函数,M、N分别为测区数据的行数与列数.
为了对两个水平分量的滤波结果进行组合与增强,我们用THEG表示增强后的总水平分量,其表达式为:
(4)
应用航磁水平分量进行边界识别时,在识别埋深较大的地质体边界、平衡高幅值与低幅值异常等方面,其识别能力具有一定的局限性.在均衡不同幅值的场源信号方面,Ferreira等(2013)通过斜导数对总场异常的总水平导数结果进行均衡增强,此方法以极大值形式体现场源边界,同时,均衡了不同埋深的异常源的信息.因此,我们采用斜导数法对THEG方法的结果进行均衡,即基于Gabor滤波的总水平分量边界增强均衡方法(THEGB),其表达式为:
(5)
THEGB方法的计算结果在(-π/2,π/2)之间,以极大值形式描绘场源边界,并且对于不同埋深的场源体异常具有均衡作用.
2 组合模型试验
2.1 垂直磁化
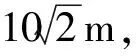

图1 组合模型三维位置示意图
图2为正演得到的组合模型磁总场、北向分量和东向分量异常平面等值线图.总场异常(图2a)范围为-2.67~22.57 nT;北向分量异常等值线呈现出南正北负、具有明显的东西走向的特征(图2b),异常范围为-15.30~15.30 nT;东向分量异常等值线呈现出东负西正、具有明显的南北走向的特征(图2c),异常范围为-15.28~18.32 nT.北向分量与东向分量异常等值线圈闭的分布位置与形态,体现了水平分量数据具有方向性的特点.由于P3的埋深相对较大,使得图2中异常等值线强度均相对较弱.
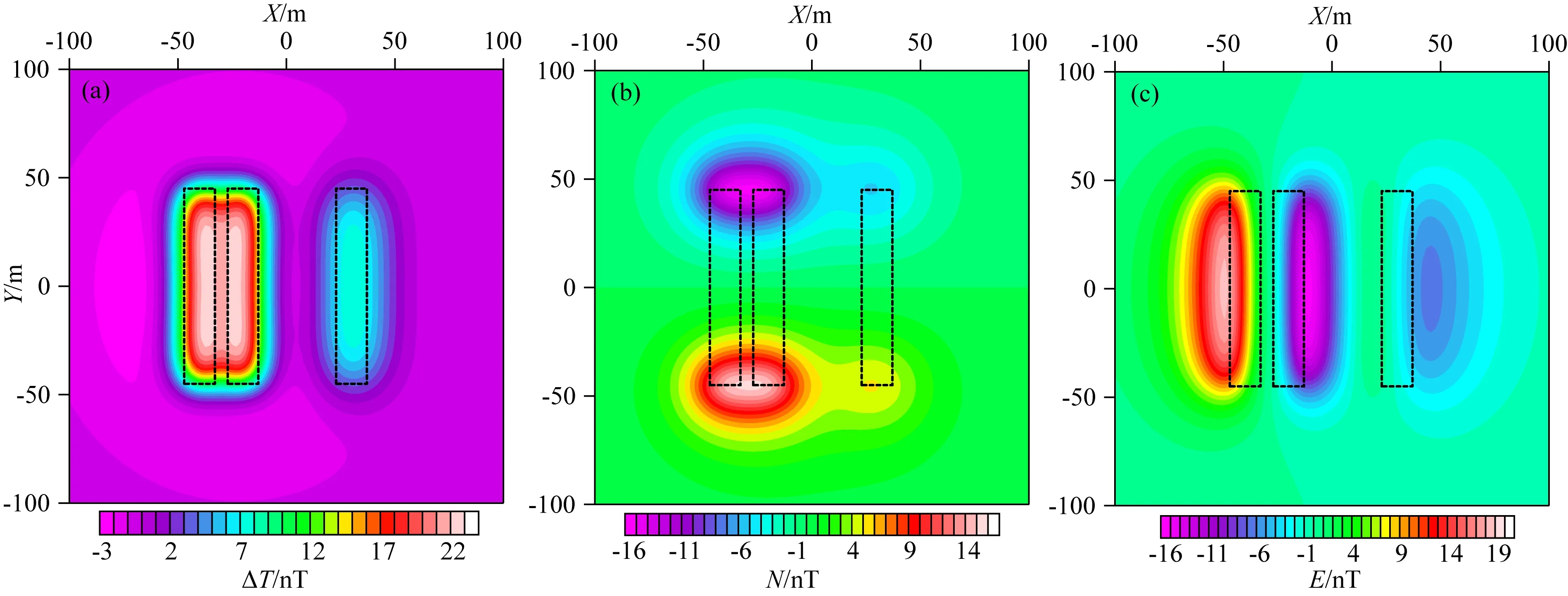
图2 组合模型异常等值线
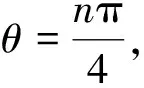
由图3可知,水平分量THEGB方法处理结果的极大值区域描绘了模型体的边界,模型体P3由于埋深相对较大,原始异常幅值较小,通过斜导数的计算,对于P3的边界信息进行了有效均衡.图3a—c中,随着σ取值的逐渐增大,等值线梯级带收紧,对于边界的增强效果更加明显.而随着σ取值的继续增大(图3d—f),在实际地质体边界周围逐渐出现了虚假的边界信息,当σ增大到4.5时,模型体周围的虚假异常幅值与实际地质体产生的边界异常幅值相近,影响了对于边界的判断和识别.我们选取了THEGB的处理结果(σ=(3,3.5))与现有的总场异常边界识别结果进行对比分析,其对比图如图4所示.
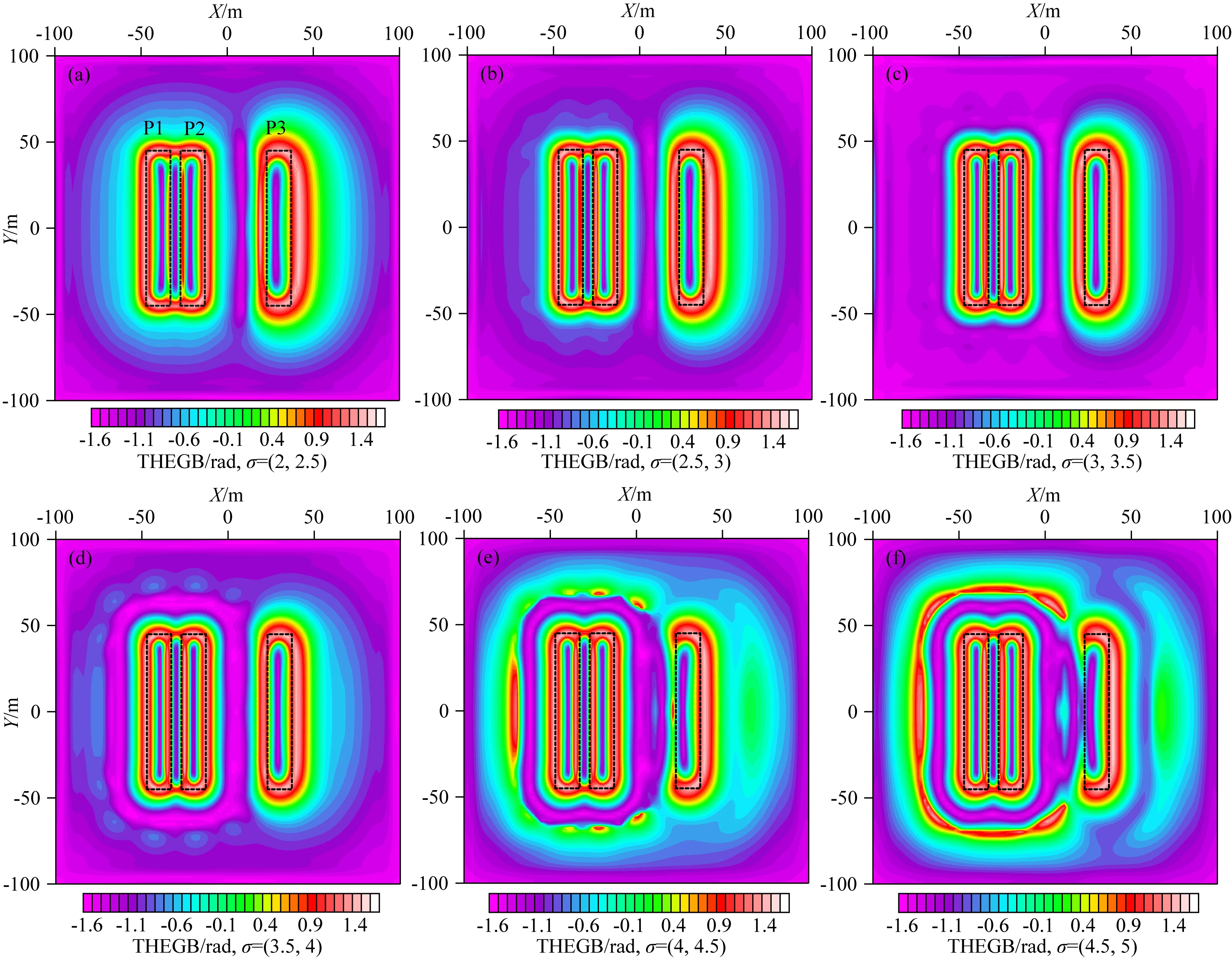
图3 组合模型不同滤波参数的水平分量THEGB处理结果
Cordell(1979)提出的总水平梯度法(THDR)的处理结果如图4a所示,等值线的极大值较好的描绘了模型P1和P2的边界位置,但由于两个模型距离较近,P1的东部边界和P2的西部边界在识别结果中并没有显示.而P3的识别结果受埋深的影响较大,等值线幅值较低,且向模型体外部扩散.图4b显示了解析信号振幅方法(ASA)(Nabighian, 1972)的处理结果,利用等值线的极大值确定场源位置.图中P1和P2的异常幅值较强,但受近距离地质体的影响,极大值圈闭的形状发生弯曲和偏移,P3处无明显的异常信号.Miller和Singh(1994)提出的斜导数法(TDR)能够有效均衡不同埋深的异常体的信息,图4c中P3的异常信息得到了有效均衡,零值线清晰地刻画了P3的边界.但其识别结果中,P1和P2被识别为一个整体,分别缺少东部和西部边界.为了提高边界识别方法的横向分辨率,Wang等(2009)提出了归一化总水平导数垂向导数方法(NVDR_THDR),其计算结果示于图4d,图中对于P1和P2之间的两个边界的信息仍有缺失,P3的异常在一定程度上得到了增强,但与埋深较浅的地质体的异常幅值仍存在差异.Ferreira等(2013)提出的总水平梯度斜导数方法(TAHG)能够均衡深源与浅源信号,其极大值指示异常体边界,但P1与P2仍缺失中间的两条边界信息.图4f为本文提出的THEGB方法处理结果,其极大值位于模型边界位置,P3的异常得到了较好的均衡,其异常幅值与P1和P2的异常幅值相近.同时,清晰地刻画出了P1的东部边界和P2的西部边界,并且异常等值线连续性较好、各边界的异常强度分布均匀、异常的边界信息保留较为完整.

图4 不同边界识别方法处理结果对比
在垂直磁化的情况下,相比于图4a—e五种方法的处理结果,THEGB方法的极大值区域描绘了模型体的边界,在有效均衡深部异常的同时,提高了边界识别的横向分辨率,保留了相邻异常体P1和P2完整的边界信息.
2.2 噪声影响
为了检验THEGB方法在噪声影响下的边界识别能力,在组合模型中加入了振幅为异常振幅0.2%的均匀分布的随机噪声,其尺寸和物性参数与2.1节中的模型体相同,图5为σ取值从2~4.5的THEGB处理结果.由图5a—d可知,随着σ取值的逐渐增大,模型体边界处的异常被逐渐增强,异常的等值线更加连续圆滑.P3受埋深和噪声的影响,模型边界处的等值线发生扭曲变形,而经过均衡后其异常幅值与P1和P2相近,极大值区域较好的描绘了模型的位置与形状.同时,σ取值的增大对于模型内部及边界处的噪声具有抑制作用.当σ继续增大时(图5e—f),模型外部产生了一些虚假的边界信息.因此,在进行实际数据处理时,σ值的选取应该平衡滤波器在压制噪声和提高边界识别能力两方面的作用.同样,我们将THEGB与现有的总场异常处理结果进行对比分析(图6).
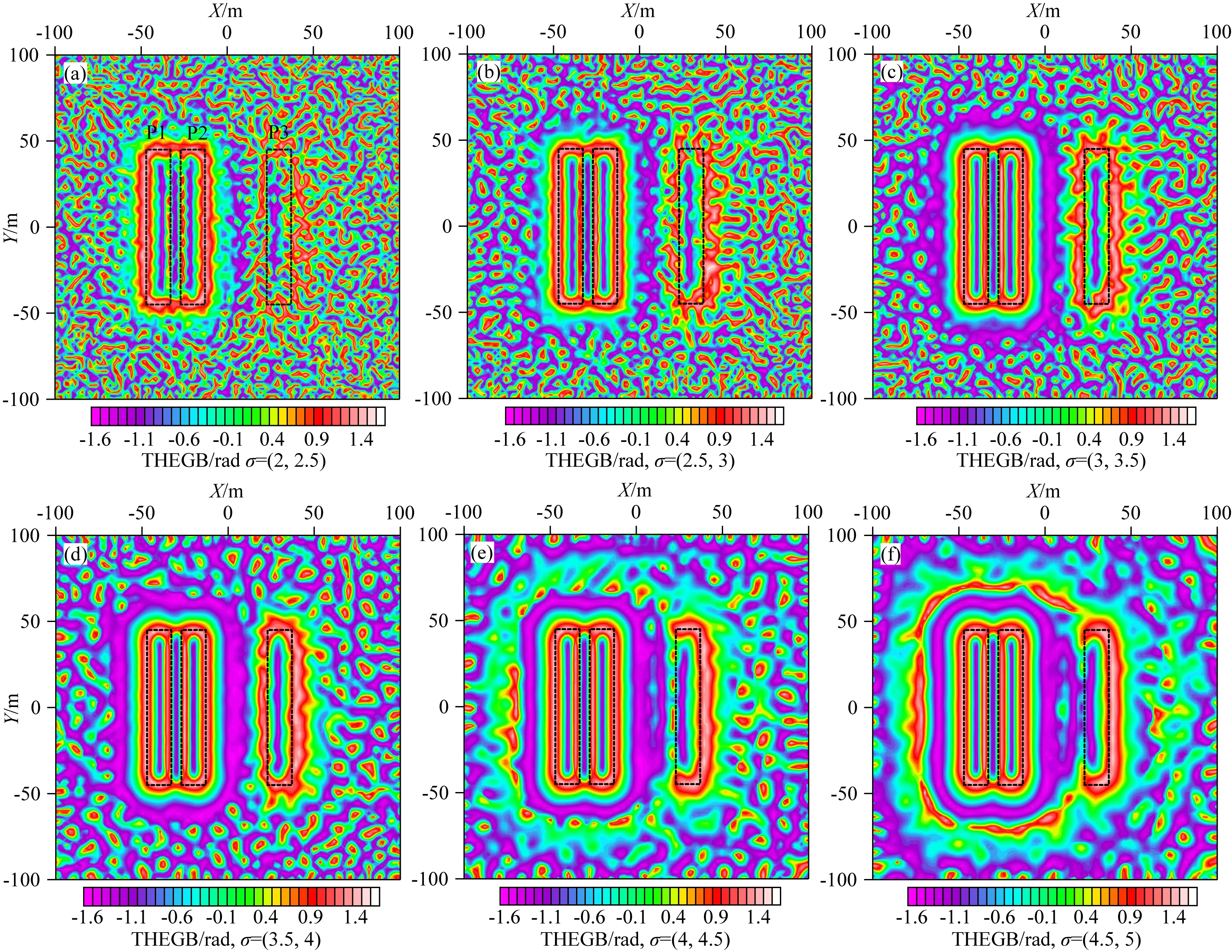
图5 噪声影响下组合模型不同滤波参数的THEGB方法处理结果
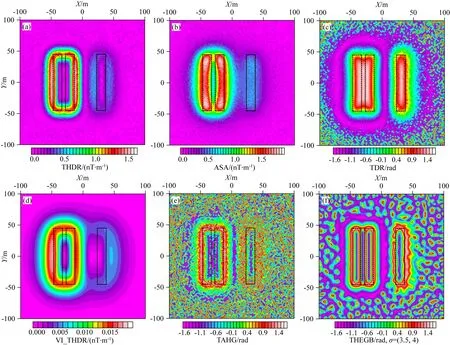
图6 噪声影响下不同边界识别方法处理结果对比
导数类的边界识别方法对噪声较为敏感,在一阶导数处理结果中(图6a—c),噪声影响遍布整个观测平面,包括模型体内部和外部空间,等值线发生扭曲变形.为了降低噪声影响,胡斌(2019)应用垂向积分的水平梯度模方法(VI_THDR)处理包含噪声的模型磁异常,而垂向积分相当于低通滤波器,对噪声具有抑制作用,其处理结果显示(图6d),垂向积分计算有效的抑制了噪声影响,但对于P3几乎没有有效的异常信号,同时,P1和P2的异常等值线略向异常体外部发散.而高阶导数类计算方法受噪声影响大,图6e显示的TAHG方法的处理结果中,P3几乎没有识别到有效的异常信号,P1与P2受到噪声影响,等值线也发生了扭曲变形.图6f为THEGB方法的处理结果,P1与P2模型边界处的异常等值线受噪声影响较小,等值线较为光滑,极大值位于模型体边界上.同时,P1的东部边界和P2的西部边界也有较好的识别效果,未受到噪声的影响.P3的异常等值线发生扭曲变形,但异常强度得到了很好的均衡.
在加入噪声的情况下,THEGB方法能够有效抑制模型体边界及内部的噪声影响,在模型边界处具有相对光滑的边界识别结果,同时保留了在没有噪声影响时所具有的横向分辨率高、均衡浅部和深部异常的特征.在实际数据处理过程中,对于信噪比较低的数据,需要先进行去噪处理,便于后续对处理结果的解释和推断.
2.3 斜磁化影响
为了检验THEGB方法在地磁场斜磁化和剩磁影响下的边界识别能力,将模型中的地磁倾角和地磁偏角设置为(I,D)=(70°,10°),模型P1、P2和P3分别具有一定大小的剩磁倾角和偏角,其中(Ir1,Dr1)=(70°,10°),(Ir2,Dr2)=(60°,20°),(Ir3,Dr3)=(45°,45°).图7显示了斜磁化影响下不同边界识别方法处理结果的对比.Cooper(2014)提出了解析信号斜导数方法(ASA_TDR)减少斜磁化的影响,其处理结果显示(图7a),P3的异常信号强度得到了有效均衡,但其等值线极值圈闭的形态和位置向东部偏移.P1和P2的边界识别结果与垂直磁化情况下的识别结果相近,在一定程度上减低了斜磁化的影响.TAHG方法的处理结果(图7b)受斜磁化影响较大,P1和P2的异常等值线向西南方向偏移,P3由于受剩磁倾角和偏角的影响更大,向西南方向偏移的更明显.同时,在模型的东北部出现虚假的异常信息.图7c为水平分量THEGB方法的处理结果,P1与P2的识别结果略向西南方向偏移,但其偏移量较TAHG方法小,受剩磁影响P3的等值线向西南发生明显偏移.
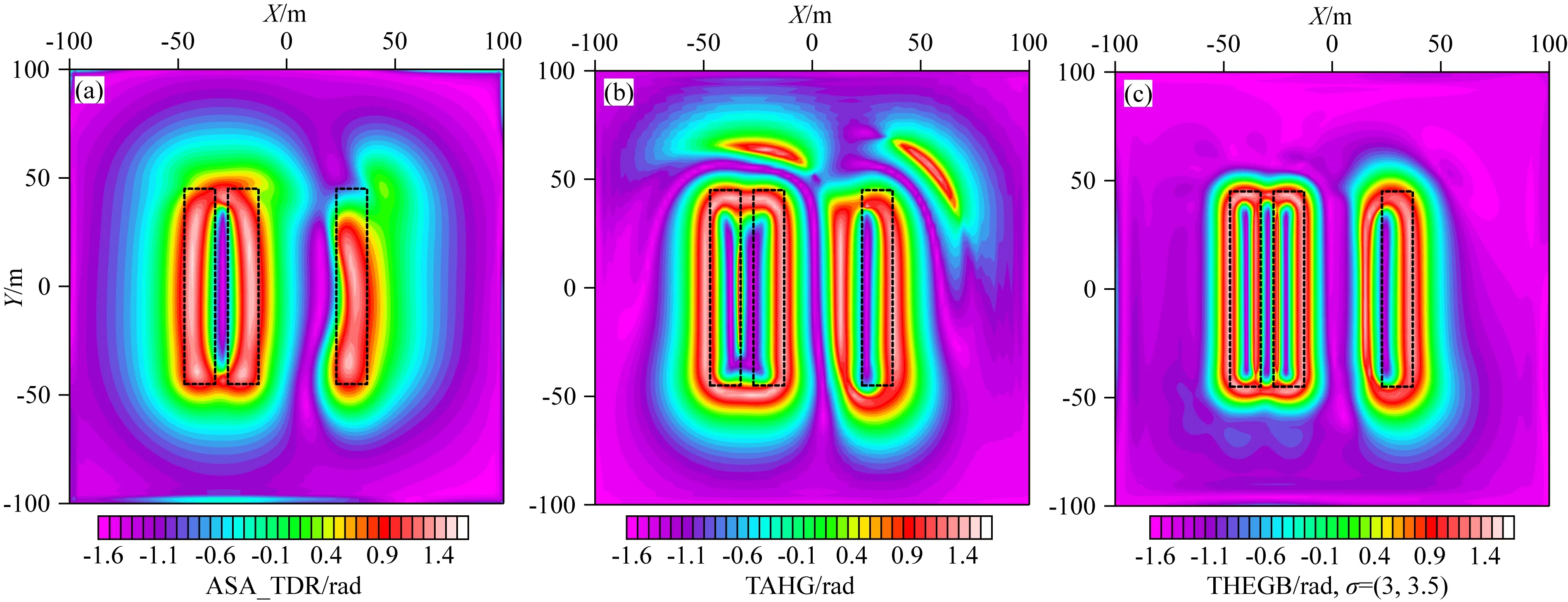
图7 斜磁化影响下不同边界识别方法处理结果对比
在地磁场斜磁化以及剩余磁化的影响下,THEGB方法的等值线发生了偏移,但当无剩磁影响或剩磁影响较小时(P1和P2)其偏移量比传统方法小.同时,保持了垂直磁化情况下横向分辨率高、均衡不同埋深异常信号的特征.因此,在实际数据处理前,应对数据做化极处理,消除地磁场对异常形态的影响.
2.4 叠加组合模型
由于磁异常数据反映的是地下磁性体共同作用所产生的异常,因此,我们设计了叠加分布的组合模型,检验THEGB方法在提高边界识别横向分辨率与垂向分辨率方面的效果.图8为叠加模型的三维位置示意图,图中模型体的尺寸参数和物性参数与图1中的模型相同.模型P1、P2和P3的中心点水平位置相同,P2和P3分别绕中心点旋转45°和-45°.P1—P3的埋深从浅至深分别为20 m、25 m和30 m,不同边界识别方法的处理结果示于图9.
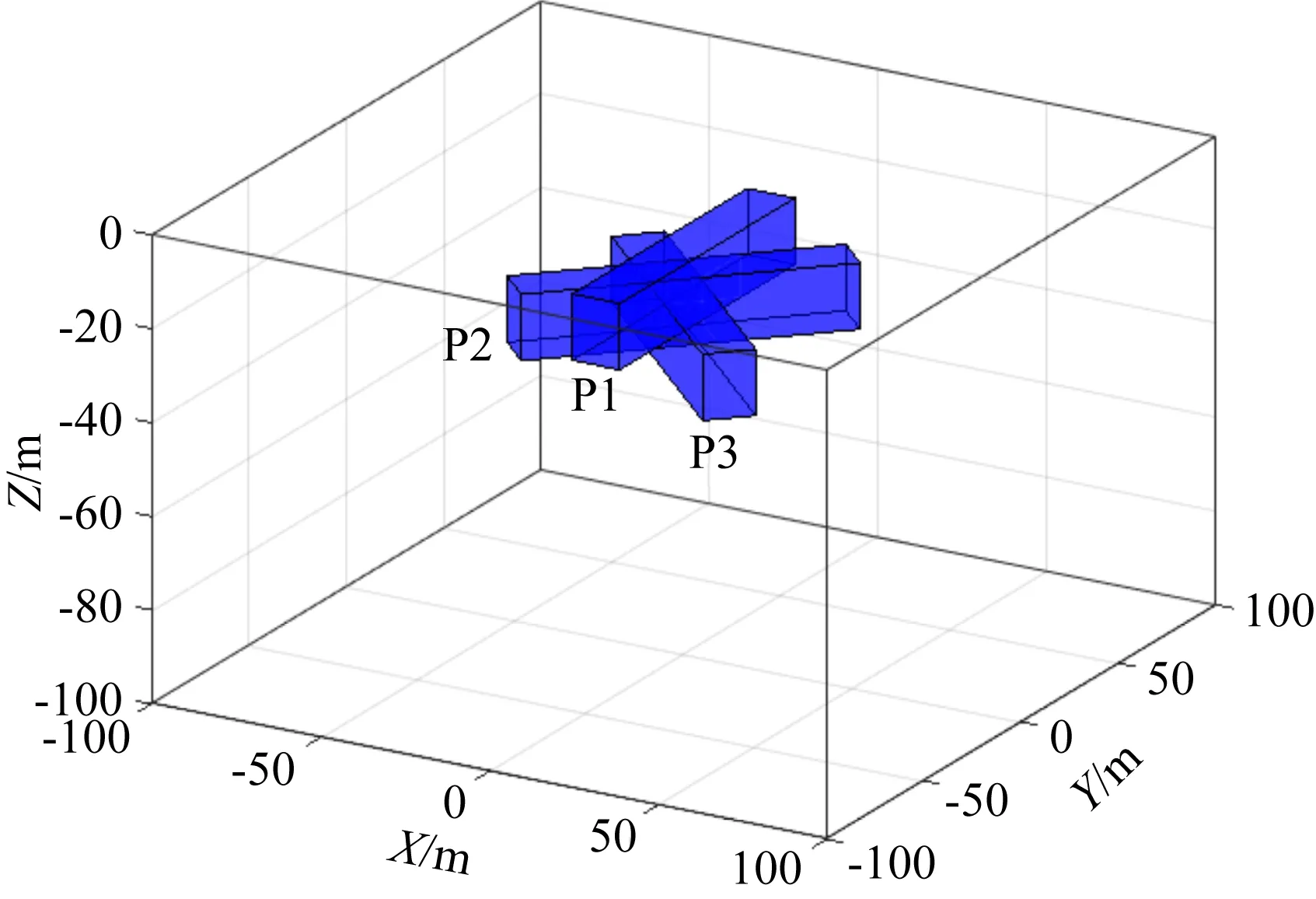
图8 叠加模型三维位置示意图
归一化总水平导数垂向导数方法(NVDR_THDR)的处理结果中(图9a),未旋转且埋深较浅的模型P1的异常信号强度较强,比较准确的描绘出P1的平面位置,但是四个方向的边界处的异常强度分布不均匀,在模型体相交的位置异常幅值突然变强或变弱.斜导数总水平导数方法(图9b)(Verduzco et al.,2004)中对于模型体的位置和形态刻画不清晰,仅在P1和P2的模型两端识别出有效信号,P3的异常幅值较弱,且等值线向模型外部发散,整体识别精度不高.THAG方法(图9c)对于P1和P2的识别效果较好,但对于P3异常均衡效果相对较弱.THEGB方法(图9d)中对于P1的识别效果较好,等值线连续、幅值分布均匀,随着埋深的增加,识别出的有效信息逐渐减少,但等值线极大值基本描绘出了模型体相应位置的轮廓,并且P3的异常信息得到了有效均衡.

图9 叠加模型不同边界识别方法处理结果对比
在不同埋深的地质体叠加作用影响下,THEGB方法能够有效均衡深部与浅部的异常信号强度,随着埋深的增大,识别出的边界信息逐渐减少,但并未影响其描绘的边界位置与形态,更有利于后续的解释与推断.因此,THEGB方法在叠加模型的应用中,同时提高了边界识别的横向分辨率与纵向分辨率.
2.5 小结
通过理论模型试验可知,本文所提出的航磁水平分量数据的均衡滤波位场边界增强方法(THEGB)能够有效均衡深部与浅部的异常信号,使深部的弱异常得到有效增强.同时,在模型体间距较近或叠加分布时,其识别结果能够很好的保留模型体的原始形态,具有较高的横向分辨率.此外,本方法能够有效压制模型内部及边界处的噪声影响.但是,滤波参数的选取需要平衡滤波器在压制噪声和增强边界两方面的作用.在应用本方法进行边界识别时,需要先进行化极处理.
3 实测数据应用
研究区地处中国新疆启鑫地区,位于中亚造山带南缘,塔里木板块东北缘北山裂谷构造带核部,古生代以来区内经历了一系列的碰撞造山、伸展挤压运动,是我国西北地区重要的多金属成矿带.北山地区构造总体呈北东-北东东向展布,主要受卡瓦布拉克—红柳河深断裂、白地洼—淤泥河深断裂、红十井—矛头山大断裂、白山大断裂共同控制(周济元等,2000;龚全胜等,2003;杨合群等,2006;刘振涛等,2007;朱江,2013;阮班晓,2017).图10为研究区地质简图,F-a—F-l为区内主要断裂构造,呈北东东、北东和北西向展布,白山大断裂(F-j)部分区段出露于研究区南部.图中F-a—F-l的分布位置与形态能够进一步验证THEGB方法的结果,同时,对研究区线性构造的推断与解释提供参考.
研究区内岩浆活动强烈,侵入岩分布较为广泛.区内的基性、超基性岩一般具有一定的磁性,且变化范围较大,能够引起不同程度的磁异常;中酸性岩体中的闪长岩磁性较强,属中强磁性,磁化率值一般在数百~数千(×10-5SI),通常会引起明显的磁异常;而火山岩具有较强的磁性,会引起明显的条带状磁异常;沉积岩通常表现为无磁性或弱磁性.
区内实测航磁数据是中国自然资源航空物探遥感中心于2018年应用搭载了自主研发的AGS-863航空磁矢量测量系统的Y-12固定翼飞机飞行测量获得,其矢量测量系统具有较高的精度与稳定性,为获得高精度的航磁矢量数据奠定基础(Xie et al.,2020).研究区测线方向分别为155°和335°,经过计算,研究区的地磁倾角为61.1°,地磁偏角为0.53°.图11为化极后的总场异常、北向分量与东向分量异常等值线图,数据的网格化间距均为150 m.由图11a总场异常等值线可知,研究区内的高磁异常等值线呈明显的北东东向、北东向分布,与区内大面积出露的闪长岩相对应.北向分量(图11b)呈现出南正北负、北东东或近东西向的异常分布特征.东向分量(图11c)呈现出西正东负、近南北向的异常分布特征.
为了消除噪声影响,分别对总场异常和水平分量进行向上延拓处理,对延拓后的水平分量进行THEGB方法处理,获取研究区的线性构造分布特征.由模型体试验可知,THEGB方法以极大值描绘场源边界,同时,场源边界在异常图中通常表现为异常梯度带、扭曲变化带、串珠状异常带和异常错位带等线性特征(杜晓娟等,2009;孙斌,2013).因此,我们结合地质图中主要断裂构造的走向、规模以及磁异常特征,利用THEGB方法的极大值进行区内主要线性构造的划分与推断,并分别将推断结果叠加在THEGB结果图(图12a)和ΔT异常等值线上(图12b).
图12显示的线性构造总体分布趋势与地质图中的断裂构造分布特征相似,主要呈北东东、北西和北东向展布.地质图中(图10)的F-a、F-b、F-c、F-d、F-e、F-h、F-j和F-k断裂在识别结果中均有所体现,特别是F-h与F-j的识别效果较为清晰、连续.其中,地质图中的F-h位于研究区中部,呈近东西向展布,是大面积出露的闪长岩的南部边界,其东段被沉积层覆盖而无法追踪.此断裂在图12中对应于THEGB方法识别出的构造线F10,图中F10是不同走向线性构造的分界,北部的线性构造呈近东西向展布,南部主要呈北东向展布.同时,F10也是研究区中部高磁异常体的南部边界,控制了中部闪长岩、花岗岩的分布;地质图中F-j是区内白山大断裂的部分区段,对应于图12中THEGB方法识别出的构造线F15,图12a中F15的异常信号清晰、连续,表现为明显的线性异常带,成北东向展布.磁异常图12b中,F15是不同异常特征的分界线,北部为大面积的正值区,南部为负值区,期间分布小范围正异常.综合地质图中的主要断裂的对比分析,THEGB方法识别出的线性构造与已知断裂有着较好地一致性,而且识别结果包含了更丰富的细节信息.为了综合分析此方法的应用效果,对总场异常分别进行了总水平导数法、解析信号振幅法、斜导数法、斜导数总水平导数法和总水平导数斜导数法处理,结果示于图13,图中黑色实线方框为对比区域.
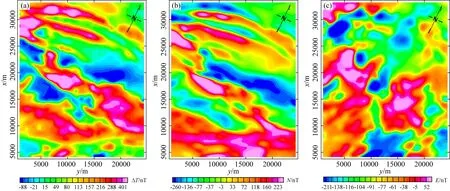
图11 研究区化极后的异常等值线图

图12 研究区断裂构造推断结果图

图13 实测数据不同方法处理效果对比
由图12和图13综合分析可知,研究区共识别出29条线性构造,分析认为F1—F17为区内主要断裂构造,F18—F29为可能存在的磁性异常体场源边界.其中,位于研究区北部的F1—F6规模较大,具有明显的北东东向分布特征,控制同样是北东东向展布的高磁异常条带分布.值得注意的是,此高磁异常条带西部异常幅值高,东部异常幅值低,在地质图以及图13a、b的识别结果中缺失东部的异常信息,而THEGB方法对弱异常进行了有效均衡和增强;F9分布于沉积岩内,磁异常表现为较大范围的负异常区,呈北东向展布,在图13a—d的识别结果中无异常信号,仅在图13e中有较弱的异常信号,而THEGB方法中F9具有明显的线性特征,推测为沉积岩内的隐伏断裂构造;位于研究区中部的F10、F11和F12呈北西西和近东西向展布,控制了该区域闪长岩和花岗岩的南北边界,特别是F12的西段在其他方法的处理结果中均显示缺失或异常幅值弱,这可能是由于F12在地表并未出露,同时受距离较近的F11共同影响,但在THEGB方法中F12清晰、连续且异常幅值强;位于研究区南部的F14和F15呈北东向展布,控制了此区域较大范围出露的闪长岩的分布;F17在THEGB方法中具有明显的线性特征,控制了3组小规模的弱异常分布.此外,F18—F29的规模相对较小,识别结果的线性特征相对较弱,结合地质图中的岩性分布,推测为可能存在的磁异常场源边界.特别是F18、F19、F23和F28在其他方法的处理结果中异常信号不明显,而在THEGB方法的结果中异常特征相对独立、清晰.
综上所述,研究区内的断裂构造线主要呈北东东、北东和北西向展布,具有明显的方向特征.在实测数据应用中,THEGB方法对于幅值较弱的异常信号进行了有效均衡,所获得的异常等值线更加清晰、连续,线性特征明显,清晰刻画线性构造的平面展布与形迹.在实际应用时,需要对异常进行化极与去噪处理,并结合研究区地质概况与磁异常特征对区内的断裂构造与地质体边界进行分析研究.
4 结论
本文提出了基于航磁水平分量均衡滤波的位场边缘增强技术,并首次将其应用于理论模型和实测航磁矢量数据处理.此方法通过异常等值线的极大值描绘场源边界,其识别结果更加清晰、连续.模型试验结果表明,THEGB方法能够有效均衡不同幅值的异常信号,使弱异常得到有效增强.同时,对于相近或叠加分布的场源体,能够很好的保留模型体的位置和形态信息,具有较高的横向分辨率.在实测数据应用中,化极后的北向分量、东向分量的均衡滤波结果包含更多的细节信息,为研究区断裂构造和磁性岩体边界推断提供了更丰富的参考依据.研究认为,对航磁水平分量数据进行边界均衡增强是较为有效的位场边缘增强技术手段,充分发挥了航磁水平分量具有的方向特性优势,在航磁矢量数据处理与解释研究方面具有重要意义.
致谢感谢中国自然资源航空物探遥感中心提供实测航磁矢量数据,并允许发表数据处理结果.
