场地土层速度结构的背景噪声反演方法及其应用

荣棉水, 王继鑫, 李小军，*, 刘奥懿, 孔小山, 李航

1 北京工业大学城市与工程安全减灾教育部重点实验室，北京 100124 2 防灾科技学院河北省地震灾害防御与风险评价重点实验室，河北三河 065201

0 引言

大量震害和理论研究表明，区域近地表土层速度结构对地震动特性有显著的影响，主要表现为对地震动峰值和地震波中不同频率成分的放大或缩小，从而直接影响到地震灾害的严重程度(师黎静, 2007; 李小军等, 2020)，准确确定近地表土层速度结构对防震减灾极为重要(冯少孔, 2003).

由于钻孔、P-S波测井和地震勘探方法存在高成本、破坏环境、有地形时难开展等缺点，近几十年来，利用地表背景噪声观测反演土层速度结构的间接方法得到迅速发展.如欧洲自2001年起就设立了Site Effects Assessment using Ambient Excitations(简化为SESAME)计划(Bard et al., 2004)，致力于发展基于背景噪声的场地效应估计和沉积层速度结构反演方法.美、日、墨西哥等许多国家学者都相继研发操作简便、成本相对较低的背景噪声反演方法(Cho, 2019; Pia-Flores et al., 2017; Thomas et al., 2020).我国也有许多地震学家将噪声密集台阵方法应用于浅层速度结构的确定，取得了很好的效果(Li et al., 2020; 雷宇航等, 2021; 王宝善等, 2021).综合来看，具体到土层的速度结构的背景噪声观测记录反演，主要发展有三类方法：①用单点背景噪声的水平与竖向谱比法(均简称NHV)测定的卓越周期简单推算土层模型参数(王未来等, 2011)；②在观测区架设小孔径地震台阵，通过测定背景噪声面波相速度频散曲线反演场地下方随深度变化的速度结构(Tian et al., 2020; 王继鑫等, 2020)；③基于面波理论(van Ginkel et al., 2020)或散射场理论(Sánchez-Sesma et al., 2011)建立NHV与地下土层结构的联系，以单点或多点台阵方式反演土层速度结构以及在此基础上发展的NHV与面波的联合反演.第一类方法是根据卓越周期Tp和场地覆盖土层厚度h来估算地基上层的平均剪切波速度(VS=4h/Tp)，仅能反映场地土层的总体平均特性(Arai and Tokimatsu, 2004)，第二类方法在实际应用时需要将背景噪声探测仪器布设成一定尺度的台阵.相比较而言，第三类方法既没有台阵布设的限制，又能方便地与面波频散形成联合反演，应用更为灵活.在第三类方法中，单点NHV反演方法是多点反演的基础，因而成为当前研究的重点.

根据对引起地表NHV的噪声波场认识的差异，单点NHV反演方法大体分为三类：①认为NHV主要受背景噪声中体波成分影响，如Herak(2008)、Bignardi等(2016)用垂直入射的S波与P波传递函数的比值来计算NHV并据此发展了利用背景噪声反演浅层速度结构的ModelHVSR和OpenHVSR方法；②认为NHV主要受背景噪声中面波成分影响，如Arai和Tokimatsu(2004)在面波理论基础上发展的背景噪声反演方法，张立(2009)发展的基阶瑞利面波NHV反演剪切波速结构的遗传算法等；③认为NHV是包括体、面波两种不同类型波场共同作用的结果.Sánchez-Sesma等(2011)的研究表明，水平层状场地背景噪声波场可用散射方程来描述，该方程借助波动传播的平均能量密度建立了NHV与格林函数的关系式，首次将背景噪声波场考虑为含有体波、面波的共同作用，从理论上建立了利用基于背景噪声的地球物理特征(此处为NHV)反演场地土层模型参数的基础.随后García-Jerez等(2013)利用边界线积分对NHV的正演计算进行了改进，并结合蒙特卡洛或模拟退火建立了NHV反演方法.

从以上研究现状可知，当用不同的正演理论来解释噪声波场时，所发展的NHV反演方法也相应地存在本质上的差异.大量观测和理论研究均表明背景噪声波场是面波和体波共同作用的结果，基于散射场理论的NHV更全面考虑了不同波动类型，显然更符合观测实际，因此再回顾前述的三类背景噪声反演方法，现有基于散射场理论的NHV反演方法及实用的反演工具的开发就显得非常匮乏.已有的基于散射场理论NHV的反演方法如García-Jerez等(2016)发展的HV-Inv，其反演算法采用蒙特卡洛或模拟退火全局反演，仍存在计算效率不高、不利于快速求解等突出的问题，因此在考虑不同类型波场共同作用的前提下，发展快速有效的全局NHV反演方法是当前亟需开展的一项重要工作.

针对这一研究现状，本文基于散射场理论NHV的正演计算方法，引入遗传与模拟退火相结合的反演框架，提出了一种场地土层速度结构的背景噪声全局反演方法，利用多个算例验证了方法的合理性和适用性，并在唐山响嘡竖向观测台站场地开展了本文方法的实例应用.

1 NHV全局反演方法

1.1 土层速度结构的NHV正演方法

NHV是场地地表观测到的背景噪声的水平和竖向分量的比值，前文已述，基于对背景噪声波场的不同认识，NHV的理论计算可主要分为体波垂直入射解(Herak, 2008; Bignardi et al., 2016)、随机点源面波解(Arai and Tokimatsu, 2000)、散射场理论解(Sánchez-Sesma et al., 2011)三类.如何解释不同类型波场作用下的NHV一直是许多研究者寻求解决的难点问题，仅考虑单独某一种类型的波场(如体波或者面波)来解释NHV仍存在不足之处，散射场理论解全面考虑了背景噪声波场中体波和面波的共同作用，理论和观测结果均证实了用其解释NHV的合理性和适用性(Sánchez-Sesma et al., 2011)，本文采用该理论解作为NHV正演方法，对其简要介绍如下：

散射场理论解是随着背景噪声成像的地震干涉理论发展起来的(秦彤威等, 2021)，地震干涉理论认为，完全散射波场中任意两个观测点获得的位移记录的互相关正比于两观测点之间的格林函数(Shapiro et al., 2005)，在频率域中可以表示为以下公式(Sánchez-Sesma and Campillo, 2006; Perton et al., 2009; Sánchez-Sesma et al., 2011)：

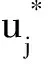
(1)

其中，格林函数Gij(xA,xB,ω)表示在xB点j方向作用的一个单元简谐点力δijδ(|x-xB|)exp(iωt)在xA点i方向引起的位移.在单元简谐点力δi jδ(|x-xB|)exp(iωt)中，i为虚数单位，ω为圆频率，t为时间.k=ω/β为S波波数，β为S波波速，Es=ρω2S2为平均S波能流密度，S2为S波平均谱密度，星号表示复共轭，Im表示给定的函数的虚部，尖括号表示平均.假定xA=xB，上式可以写为

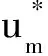
=-2πμEsk-1×Im[Gm m(xA,xA,ω)],

(2)

其中，μ=ρβ2，E(xA)为能量密度，下标m表示不同方向.该公式表明当激发力源和观测接收点重合时，能量密度与格林函数虚部成正比.当取x=0表示地表观测点，下标用1和2表示两个水平方向，3表示竖直方向，则水平和竖向谱比可写为

(3)

上式中格林函数虚部是与各土层的VS、VP、h、ρ相关的函数，由于其函数形式既涉及各层VS、VP、h、ρ组成的矩阵求解，又涉及同一土层的波数积分，函数形式较为复杂，对此，文献Sánchez-Sesma等(2011)附录中给出了分层场地格林函数虚部计算的详细推导过程和计算表达式，篇幅所限本文不再赘述.但无论格林函数虚部的计算表达式如何复杂，只要各层土体特性参数确定，则格林函数虚部也唯一地确定，这样上式就将地表平均测量值与地下介质的固有特性联系起来，本文即采用该式正演计算已知场地土层模型的理论NHV.

1.2 目标函数的确定

反演的过程就是以地表观测NHV曲线为目标提取地下一维速度结构的过程，为此需要确定一目标函数来描述反演模型的理论NHV与实际观测的吻合程度.作为对已有目标函数的改进，我们引入了斜率相关项并构建了一种新形式的目标函数(Rong et al., 2020)，其定义如下：

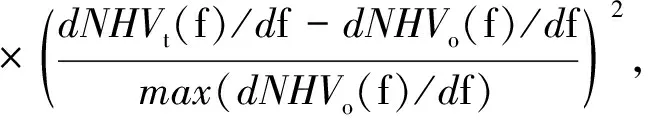
该式第一项代表模拟曲线和观测曲线幅值和谱形的差异，第二项表示模拟曲线和观测曲线之间斜率比的差异.采用两项乘积形式的目标函数将使得反演曲线需要同时拟合NHV曲线及其一阶导数曲线，从而实现多目标反演，这种多目标反演有利于结果的快速收敛，同时可以减少反演的多解性.在等式(4)中，NHVt(f)为理论NHV，NHVo(f)为观测NHV，f为频率，dNHVt(f)/df和dNHVo(f)/df分别代表NHVt(f)、NHVo(f)对频率f的一阶导数.P=(p1,p2,p3,…,pN)T是模型的参数向量，pi={VSi,VPi,hi,ρi}是第i层的参数.VSi、VPi、hi、ρi分别代表横波速度、纵波速度、厚度和密度，N表示土层总数.当N较大时，Φ(P)为多参数、多极值的非线性函数.

1.3 遗传模拟退火混合反演算法

遗传算法(GA)和模拟退火算法(SA)混合的全局优化算法已被用于土层模型参数的地震动观测记录反演(荣棉水等, 2018)，这种混合算法利用了模拟退火算法局部搜索能力强的优势避免遗传算法陷入局部极值而过早收敛，同时也利用遗传算法全局搜索能力强的优势有效克服了模拟退火算法全局搜索能力差的缺点，二者取长补短提高了反演的效率与准确性.为适应背景噪声数据的反演，本文对该混合方法进行了两方面的调整：一是不再以目标函数的精度作为反演是否结束的判断条件，而是改用预先设定的遗传迭代数来控制反演是否结束；二是不再根据目标函数的精度来进行遗传迭代过程中的早熟判断.这些调整进一步提高了反演的效率.算法简述如下：

首先用pi=(VSi,VPi,hi,ρi)表示第i个土层所需考虑的参数，i=1，2，3，…，N.设置全局反演参数，这些参数包括遗传种群大小(M)、变量维数(反演中考虑的最大变量数)、用于表示单个个体的二进制位数、SA初始温度T0和在特定温度下的迭代代数(l).然后初始化遗传种群模型，计算初始种群的目标函数值和其中每个个体的相对适应度值.模型种群中的每个个体用一串0和1的二进制码表示，其相对适应度值表达式为

(5)

(6)

(7)

适应度值是从上一遗传代进化到下一遗传代时对个体进行优胜劣汰的依据，根据适应度值进行遗传的选择、重组或变异操作.种群中个体的适应度值越大，其被复制并传递到下一代的概率就越高.完成遗传操作后父代种群就可以进化生成子代种群.

完成遗传操作后，对于新生成的子代种群，再引入SA操作以减少GA的过早收敛.在这个操作中，我们先比较子代种群中每个个体(Φchild)与其父代种群中相应个体(Φparent)的目标函数，然后计算它们的差值(ΔΦ=Φchild-Φparent).当差值ΔΦ<0时该个体可继续遗传到下一代，当差值大于零时，则给定一个随机扰动值，按照当前模拟退火的温度值计算接受新个体的概率值exp(-ΔΦ/Tk)，如果该个体的接受概率大于随机扰动值，则接受该子代个体加入当前的种群，参与后续的遗传进化，否则不接受该子代个体.接受概率计算式中Tk是SA第k次迭代的温度，Tk随着迭代代数(l)的增加而减少，其按下式计算获得：

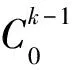
(8)

式中C0为温度衰减系数，通常是一个小于1的常数.通过遗传和模拟退火操作的组合，反演循环计算设定的最大遗传代数，并给出所反演的参数模型空间的最优解.为了更清晰地展示本文混合GA和SA全局优化算法的完整框架，用图1给出了反演计算流程图，从该图也能看出反演涉及的主要步骤如下：

图1 反演流程图

(1)生成初始种群；

(2)设置全局反演参数(模拟退火的初始温度、最大遗传代数、交叉率、变异率等)；

(3)根据遗传代数进行循环计算.计算当前遗传代下所有个体在当前温度下的NHVs和目标函数，之后根据目标函数计算种群的适应度值；

(4)执行每一代循环的GA操作，进行选择、重组和变异；

(5)执行SA操作，比较子代个体(Φchild)和父代个体(Φparent)的目标函数，判断在当前温度下子代个体是否能依据给定的随机扰动以可接受的概率被替换，依据最大遗传代数不断循环；

(6)输出最优解，结束反演过程.

2 反演方法的验证

2.1 反演参数的敏感性及反演策略的确定

前文已述对于每一层土体，都有VP、VS、h和ρ四个参数，当需考虑的土层数目较大时，模型空间将变得很大，会显著降低反演计算的效率.进行参数的敏感性分析可以明确对NHV起主要影响作用的模型参数，忽略影响极小的参数，从而降低模型空间的维度，节约计算资源.为了量化参数的敏感性，本文采用Arai和Tokimatsu(2004)参数敏感性的定义，用一无量纲偏导数的绝对值来表征反演模型参数的敏感度，其公式表示如下：

(9)

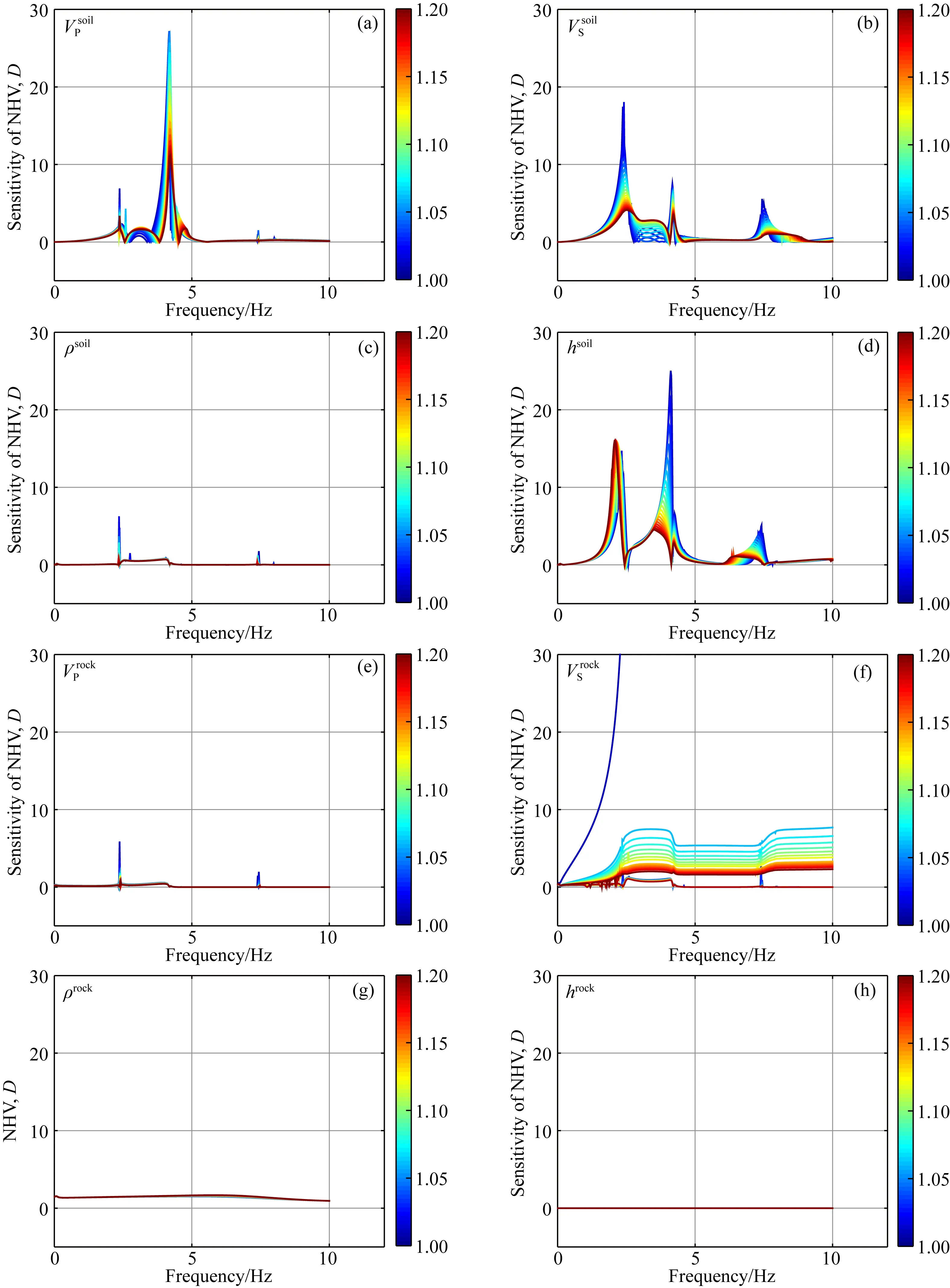
图2 简化模型的参数敏感性

表1 简化的土层模型

2.2 目标NHV曲线随机扰动后的反演实例

为了验证本文方法，从多个KiK-net台站中选择了符合一维场地假设(Thompson et al., 2012)的FKSH14台站场地作为一实例.KiK-net网站提供了该台站场地地面以下106 m的PS波测井记录，考虑到使算例模型中理论计算的NHV曲线能完整地体现该场地的深部和浅部特征，引用日本地震危险性信息站(J-SHIS)给出的FKSH14台站深部模型将其速度剖面延伸至地震基岩，但由于J-SHIS模型浅部信息较粗略，该模型第一层土厚度为170 m，我们将106～170 m范围的土层分为两层，其中上层的波速与PS测井揭示的工程基岩相同，下层的波速与J-SHIS模型的最上层相同，最终给出的FKSH14台站模型见表2所示.虽然本文重点关注土层的模型参数，但对于理论算例而言，给出兼具深、浅部特征的速度剖面可以为反演提供更合理的初始模型，也有利于获得深部特征对NHV影响的初步认识.

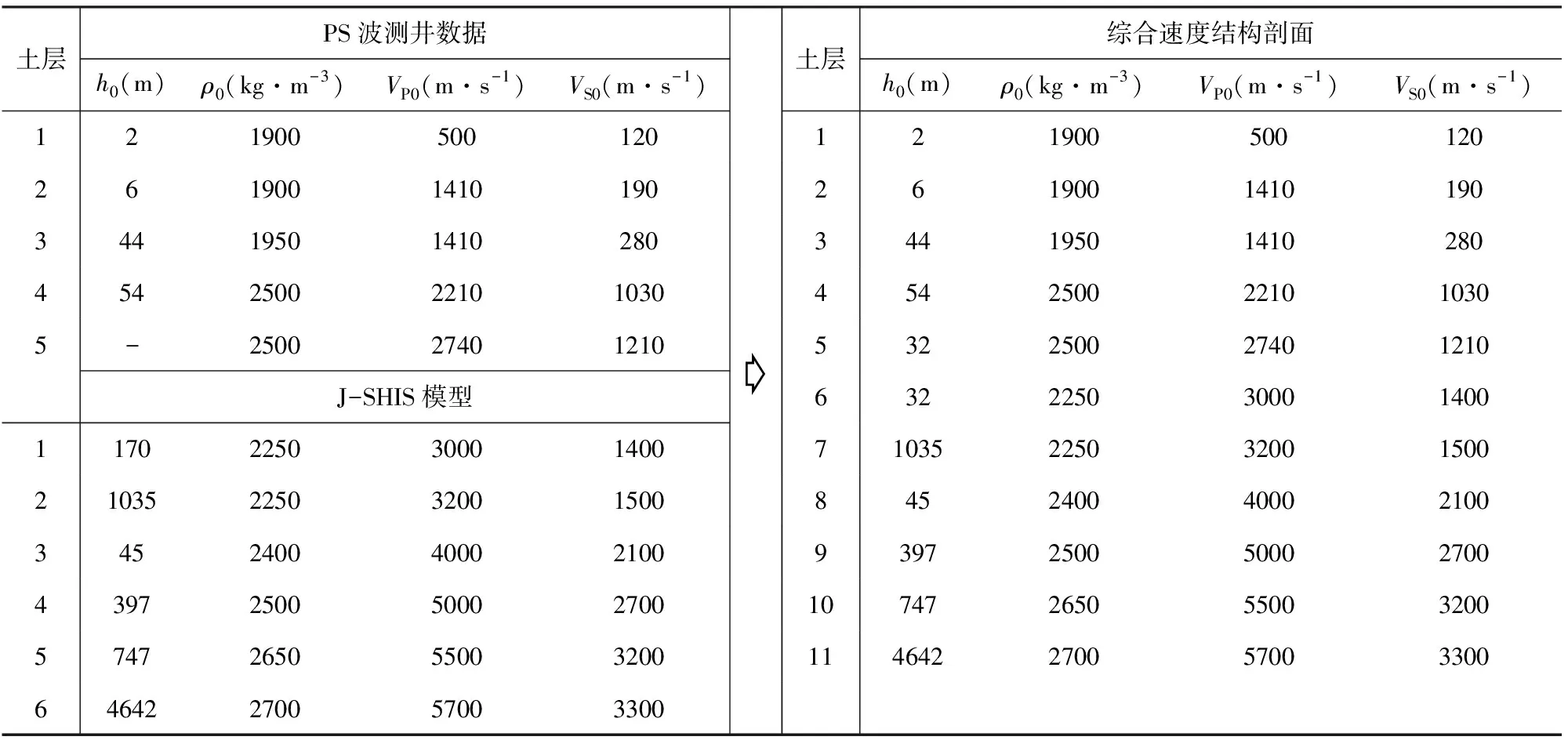
表2 FKSH14的PS测井、J-SHIS模型和下至地震基岩的综合速度剖面

在反演算法的检验研究中，一般都需对反演的目标曲线增加一定程度的随机扰动以考虑反演目标曲线的不确定性，使得反演算法的检验更符合实际情况.在FKSH14场地速度剖面的理论NHV曲线上添加30 dB的随机扰动以模拟目标NHV曲线的不确定性，并将添加随机扰动后的NHV曲线作为反演目标谱，如图3a所示.不同频率下添加随机扰动后的目标谱与理论NHV谱的差异如图3b所示，可见目标谱与理论NHV曲线差异在20%范围内.确定场地反演目标NHV谱之后，在开始反演过程之前，应预先确定所有模型参数的搜索范围(即为模型空间).由于本文仅关注场地的土层速度结构，将J-SHIS模型揭示的深部速度结构取为固定值，将FKSH14场地上部四层土体取为可变值.本文对上部四层土体所有模型参数的搜索范围都是根据初始模型速度剖面确定.例如，FKSH14的压缩、剪切波速度、厚度、密度分别设置为VP0、VS0、ρ0和h0，每层参数搜索范围为0.65VP0～1.35VP0、0.65VS0～1.35VS0、0.65h0～1.35h0，每层土体密度取为固定值.

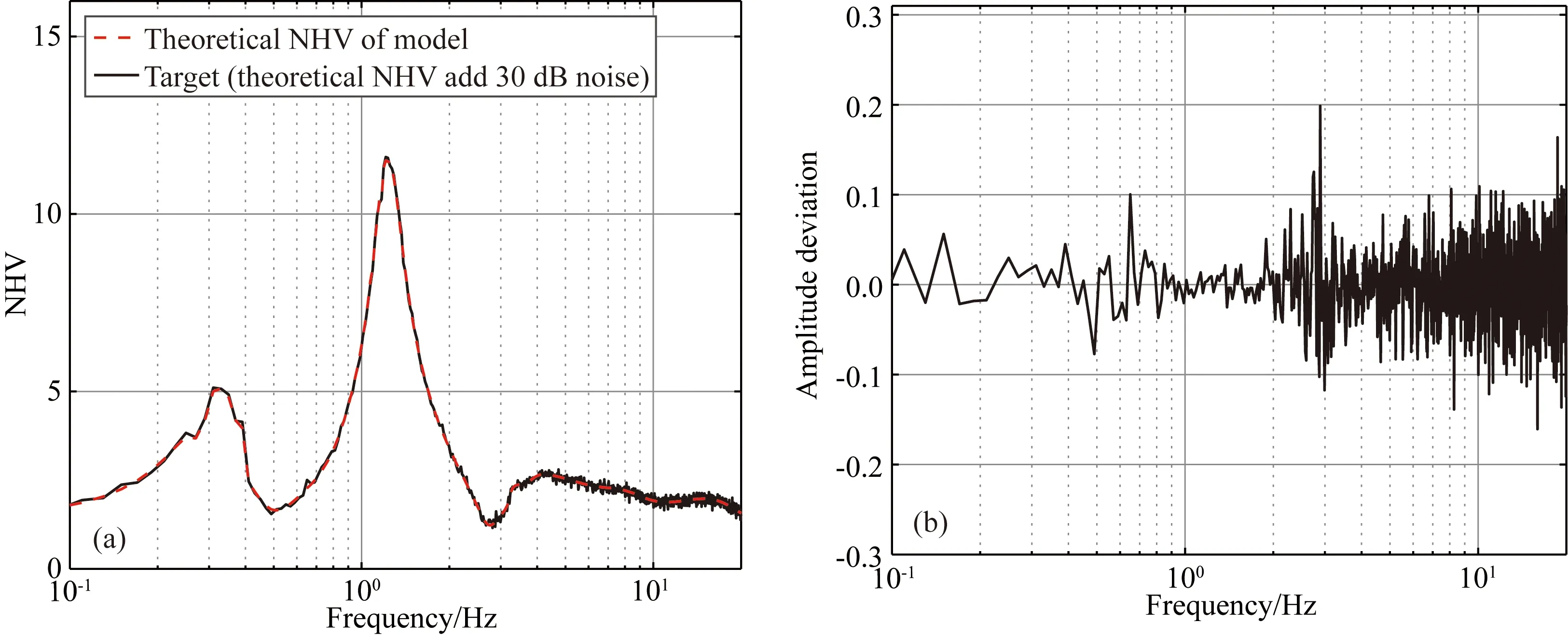
图3 反演目标曲线、FKSH14模型理论曲线及二者的差异

反演中将遗传代数取为100，每一遗传代的个体数为200.对于GA操作，代沟为0.9，交叉率为0.7，变异率为0.01.SA的初始温度设置为10 ℃，温度衰减系数C0为0.99.当遗传代数达到100代时，反演过程自动结束，得到与最小目标函数相对应的反演模型作为最佳反演模型.图4给出了反演各代的平均目标函数与遗传代数的关系，该图表明随着遗传代数的增加，目标函数快速降低，遗传40代之后目标函数曲线趋缓，此后即使遗传代数继续增加，目标函数也没有明显的降低，这也说明经过100代的遗传，获得的反演结果稳定在最佳反演模型附近.图4b给出了反演过程中所有的速度结构随模型出现先后的变化，该图表明随着遗传代数的增加，反演逐步收敛到目标模型，反演最佳模型与目标模型吻合良好.图5给出了各土层VS、h随遗传迭代次数增大的变化关系，该图清晰地显示随着迭代次数增大，各层VS、h很快收敛至某一固定值附近，表明了反演算法的有效性.初始模型、反演模型各参数的均值和方差均示于表3，由该表可知反演模型土层的参数与表2目标模型极为接近，尤其是各土层VS、h值几乎重现了目标模型.

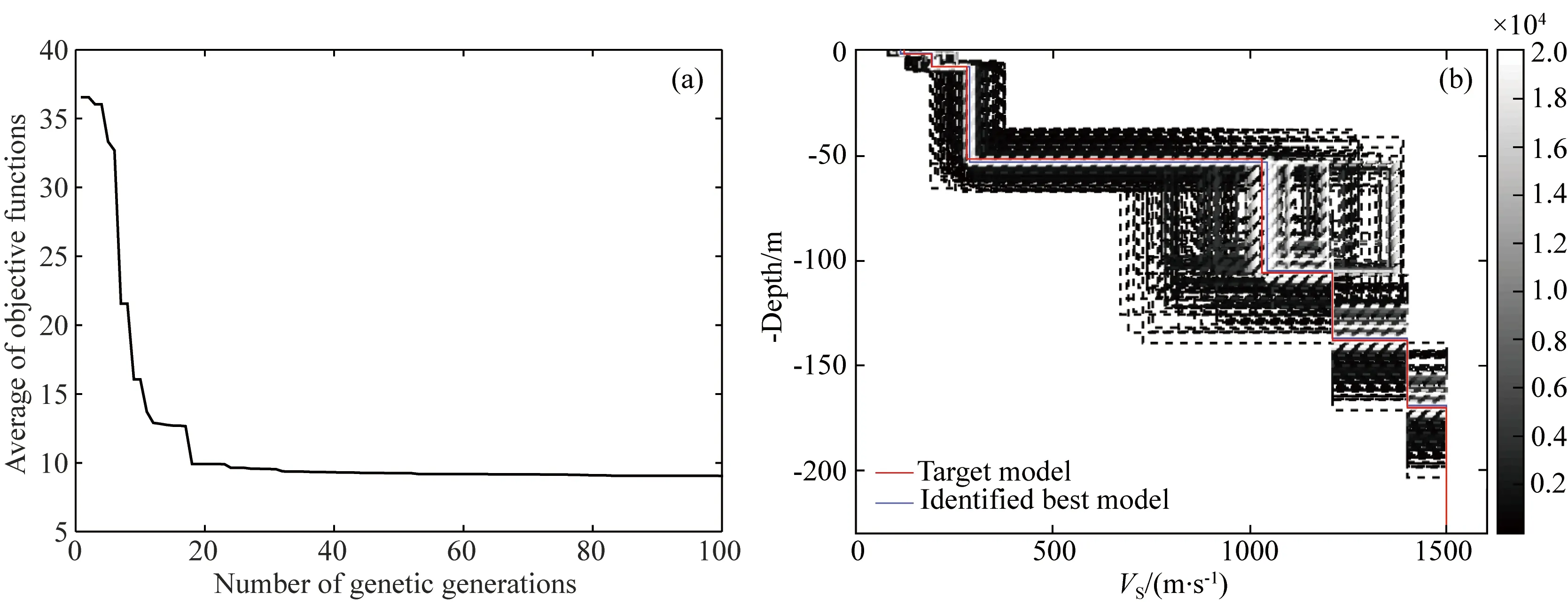
图4 目标函数变化曲线(a)及反演过程中速度结构的变化(b)

图5 各层VS与h随迭代次数增大的变化关系

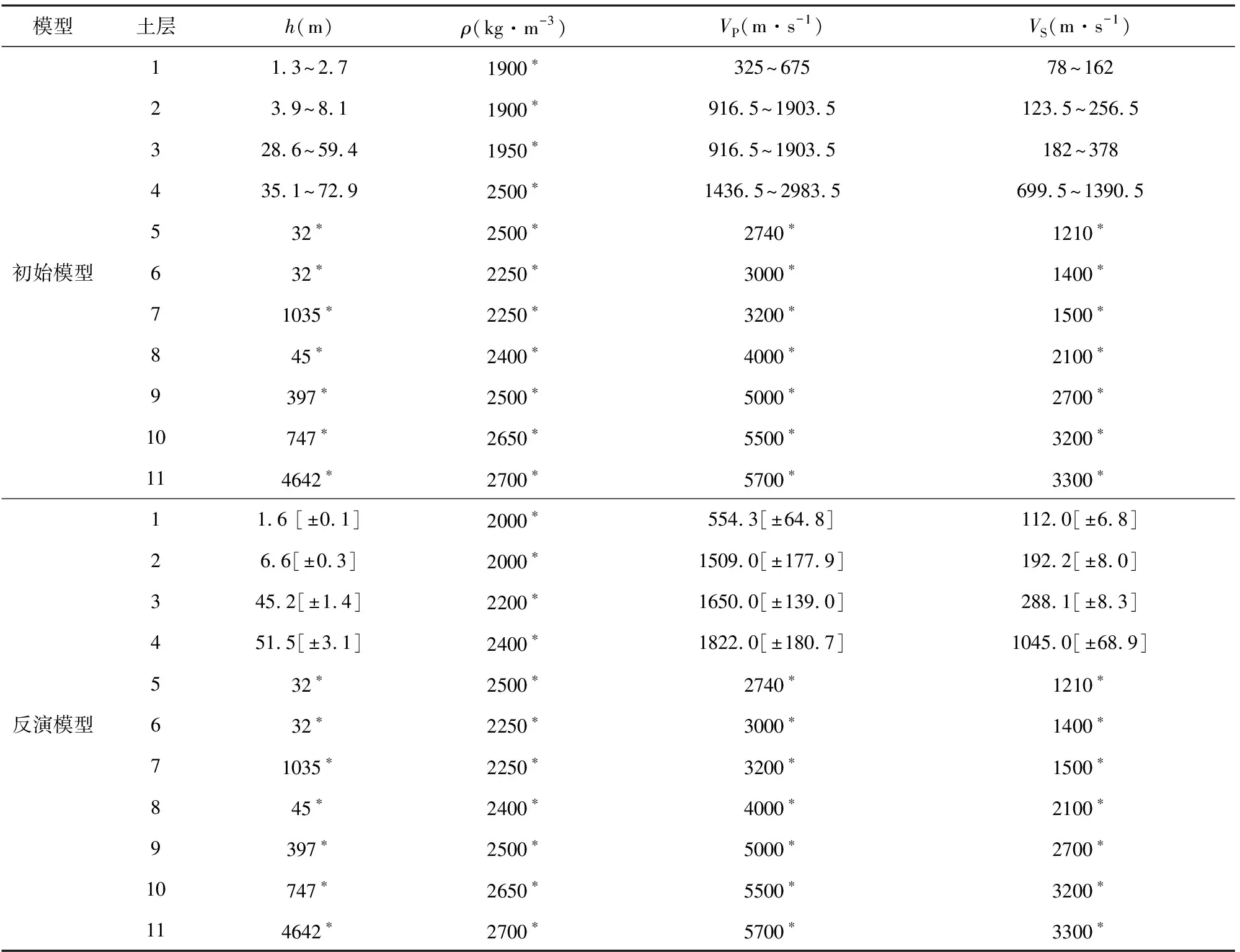
表3 FKSH14的初始模型和反演模型

2.3 对三类典型模型反演效果的验证及不同方法的比较

为了进一步验证本文方法对几类不同模型的反演效果，根据场地剪切波速变化的一般规律构建了三类典型模型，分别是剪切波速随深度逐渐变大的递增层模型、软夹层和硬夹层模型，模型参数列于表4中.反演目标谱分别取为模型理论NHV曲线添加30 dB随机扰动后的谱曲线，如图6a中黑色粗实线所示.反演中将表4所示模型剪切波速2000 m·s-1及以上的基岩层各参数取为固定值，上部三层土体的纵波、横波速度及厚度取为可变值，每层参数搜索范围为0.65VP0～1.35VP0、0.65VS0～1.35VS0、0.65h0～1.35h0，每层土体密度取为固定值.利用本文提出的反演方法和HV-Inv法分别反演100代.对于本文方法，与上一节中反演参数设置相似，将遗传代数取为100，每一遗传代的个体数为200，GA操作中代沟为0.9，交叉率为0.7，变异率为0.01，SA的初始温度设置为10 ℃，SA温度衰减系数C0为0.99.HV-Inv反演设置中采用全局的Monte Carlo法，迭代次数设置为100，扰动范围设置为5%(此值控制当前模型周围的最大扰动范围，在此范围内产生下一个模型).当代数达到100代时，反演过程自动结束，得到与最小目标函数相对应的反演模型作为最佳反演模型.不同方法反演目标函数随遗传代数的变化关系如图6b所示，由该图可知本文反演方法目标函数下降速度更快，更易趋近于稳定的最佳模型，说明本文反演方法较HV-Inv方法效率更高.图6c给出了经过相同代数的迭代之后，不同方法反演获得的最佳模型，可知本文方法与HV-Inv方法具有几乎相当的反演效果，比较而言，本文方法对岩土分界面的反演更为准确，针对软夹层模型，本文方法获得的反演模型更接近目标模型.从图6a不同方法获得的最佳模型理论NHV曲线对目标NHV曲线的拟合情况来看，本文方法与HV-Inv方法获得的最佳模型的NHV曲线均能非常好地拟合目标NHV，两种方法对目标NHV曲线的拟合效果基本相当.这一结果进一步表明本文方法适用于不同类型模型的反演.

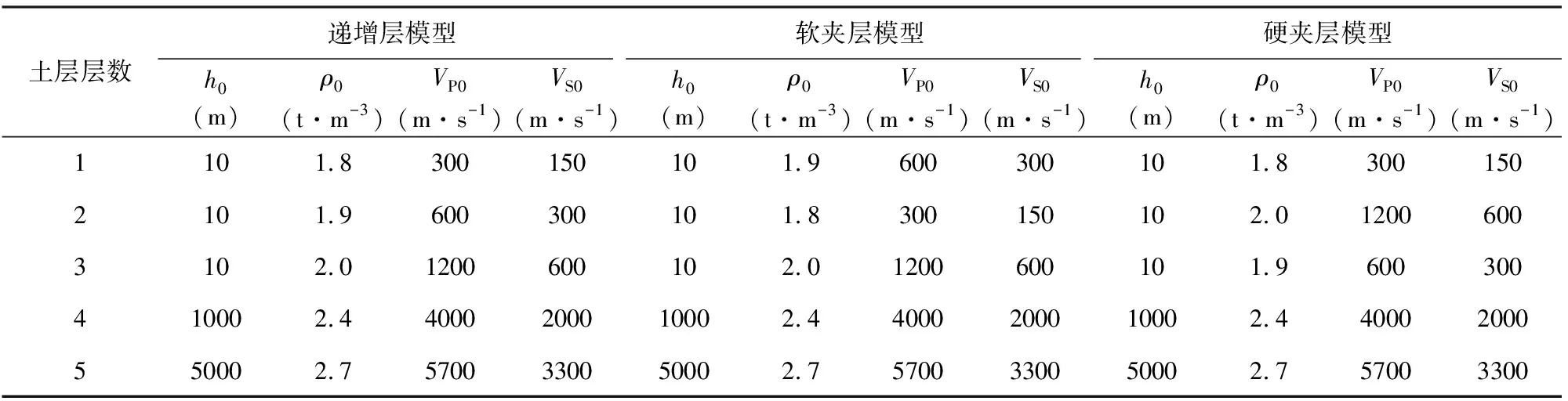
表4 递增层模型、软夹层和硬夹层模型参数

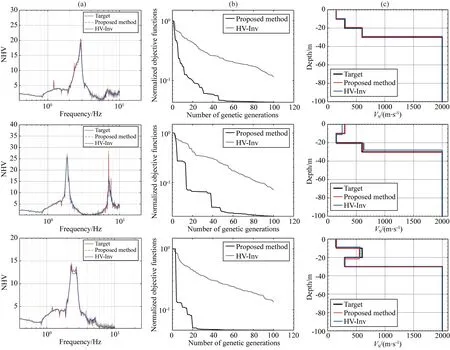
图6 不同方法对三类典型模型反演结果的比较

3 反演方法的应用实例

3.1 唐山响嘡竖向观测台阵场地及其噪声观测

本文选取唐山响嘡竖向观测台阵场地的3#测井作为观测场地，该测井穿透强风化层并到达弱风化层，井深47 m，其钻孔数据如表5所示(周雍年等, 2005).测井位于河北省唐山市滦县响嘡镇杜峪村(39.70°N，118.74°E)，地理位置示于图7.

图7 唐山响嘡竖向台阵位置示意图

笔者于2019年7月2—3日在3#测井场地布设了背景噪声观测台阵以1000 Hz的采样率进行了连续24 h的背景噪声探测实验.本文截取了最接近3#测井的观测点凌晨2∶00—3∶00的三分量记录，并进行了去均值、去趋势项等预处理.图8给出了预处理之后的三分量噪声波形记录及其振幅谱.

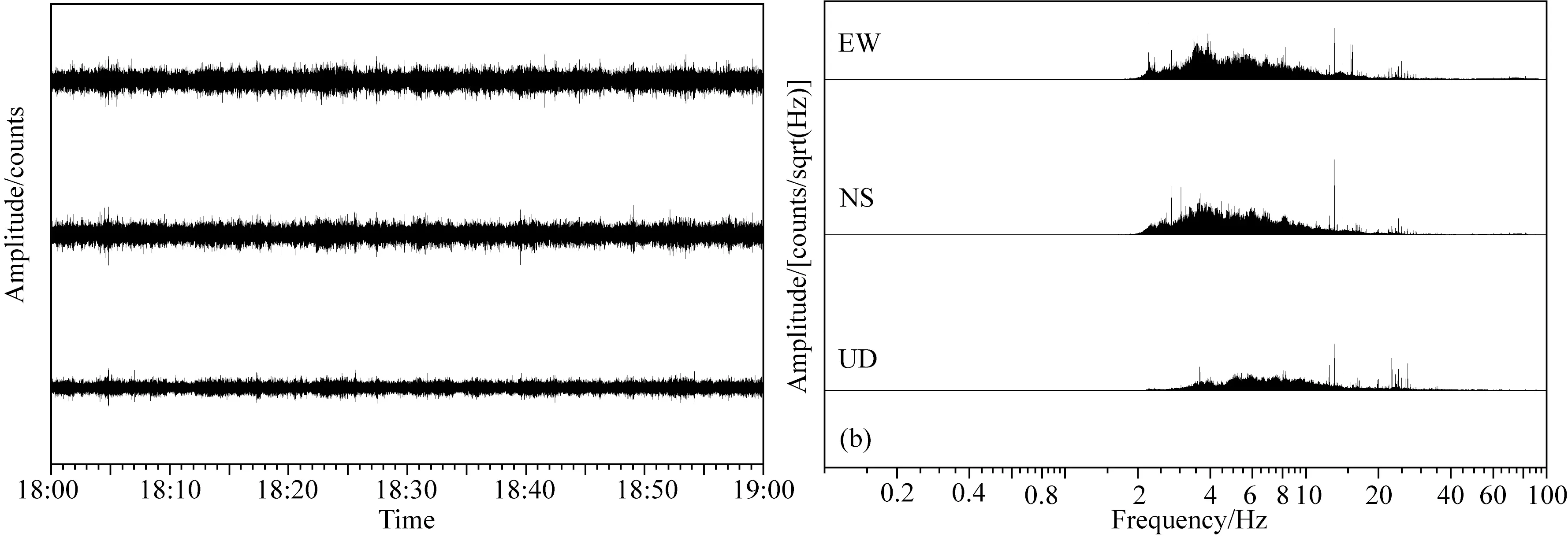
图8 试验场地3#测点的噪声观测记录

3.2 反演获得的土层速度结构模型与钻孔的比较

本文利用开源软件GEOPSY(http:∥www.geopsy.org-SESAME Project)处理噪声观测数据，该软件可在若干可选择的时间窗内计算三个分量的功率谱密度，在频域中对记录的波场进行统计分析.这些时间窗口的宽度取决于目标频带和记录长度.其中时间窗口的长度定义了可以进行合理分析的最小频率(Bard et al., 2004)，由于SESAME标准建议每个窗口至少有10个周期，因此最小频率(以Hz为单位)定义为10/lw(lw为窗口长度，以s为单位)；对于每个窗口，应用5%的锥度，以避免可能的截断效应；将反触发算法(Withers et al., 1998)应用于噪声记录序列，以便在计算中仅包括具有准平稳振幅的信号，选择标准是基于短时窗(STA)和长时窗(LTA)平均振幅的比较，STA、LTA、Min STA/LTA和Max STA/LTA的典型值分别取1、30、0.2和2.5 s，这一比率的上限旨在排除例如靠近传感器的操作人员产生的尖峰；对于所考虑的所有情况，时间窗口重叠5%；频率分析中采用了25%平滑常数的平滑函数(Picotti et al., 2017; Konno and Ohmachi, 1998)以确保低频和高频点的数量恒定.计算所得三分量功率谱密度如图9所示.

图9 试验场地3#测点观测记录功率谱

传统的NHV曲线是根据傅里叶振幅谱(FAS; 例如Bard et al., 2004)或响应谱(Zhu et al., 2020)计算.此处，文中根据功率谱密度(PSD)估算NHV曲线，其中通过矢量求和对两个水平分量求平均值，然后从PSD中获得噪声的NHV(Arai and Tokimatsu, 2004)：

(10)

式中，下标EW，NS和UD分别表示东西，南北和竖向分量.由于噪声观测结果易受环境、场地、仪器多因素影响，因此对观测NHV值还需检验其可靠性.欧盟SESAME项目(Bard et al., 2004)研究给出了检验NHV可靠性和峰值清晰度的标准(详见SESAME, 2004 “2.1结果可靠性标准”).本文依据该标准对唐山响嘡台3#场地实测NHV(见图10)进行检验，结果证实实际观测获得的NHV曲线满足其可靠性和峰值清晰度准则，可以认为唐山响嘡台3#场地实测NHV结果用于场地反演是可靠的.

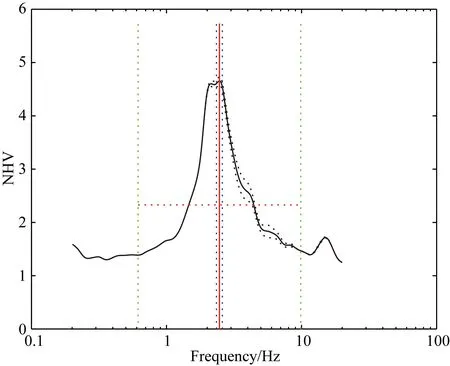
图10 唐山响嘡台3#场地实测NHV

许多研究证实NHV的空间变化与地下介质的横向不均匀性有密切联系(Macau et al., 2015; Bonnefoy-Claudet et al., 2009; Matsushima et al., 2014; Uebayashi et al., 2012).本文通过旋转实测噪声记录的东西、南北水平分量计算得到了NHV随水平面方位角的变化(见图11)，结果显示不同的水平面方位角情形下NHV频谱曲线较为一致，NHV频谱曲线随水平面方位角的变化是微小的，表明该场地在东西、南北两个水平方向仅表现出弱各向异性，将其近似为一维场地是合适的.图12给出了地表观测NHV与钻孔模型正演NHV的比较，虽然观测NHV与钻孔模型的理论NHV谱形接近，但图中也能看到二者在1.5 Hz以上频段仍有明显差异，据此可以推测反演模型的自振周期等特征可能接近钻孔模型，而分层波速等细部特征可能与钻孔存在明显差别.

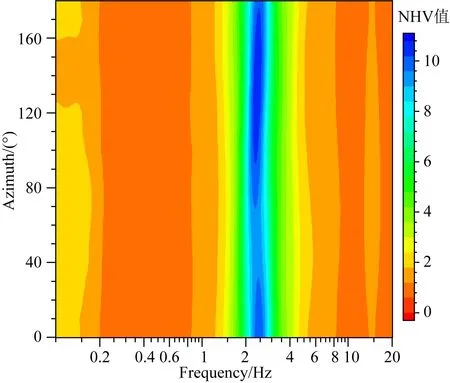
图11 唐山响嘡台3#场地基于傅里叶谱的NHV随水平面方位角的变化

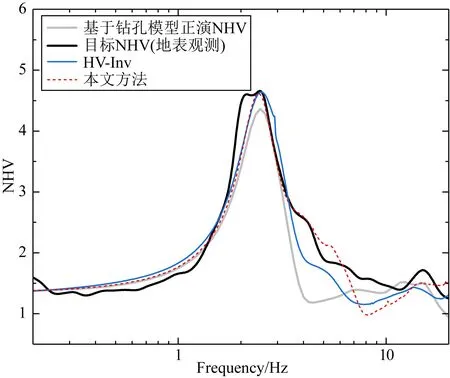
图12 地表观测NHV与钻孔模型正演NHV的比较及不同方法对地表观测NHV曲线的拟合

对土层速度结构的反演需要事先设定一个假设的初始速度结构模型.本文采用王继鑫等(2020)提取的3.5～20 Hz实测频散曲线，以0.1 Hz为步长采用改进半波长法估算出试验场地剪切波速剖面.由于本文主要关注场地的土层，岩土工程一般将剪切波速>500 m·s-1的层位定义为软基岩，借助上述改进半波长法估算的剪切波速剖面，得出剪切波速<500 m·s-1的覆盖土层厚度为29.2 m.再结合实测NHV的最高频率(20 Hz)以及频散曲线该频率下的相速度(193 m·s-1)，可以简单估算NHV曲线最高频率所对应的最小土层厚度为9.65 m，即用NHV反演所能分辨的土层厚度将不小于9.65 m.鉴于此，从工程应用角度对初始模型进行了一定简化，将覆盖土层总厚度取为30 m，并按10 m(高于最小分辨率)一层分为3层.根据此分层给出初始速度结构模型如表6所示.

随后分别利用本文提出的反演方法和HV-Inv法反演场地土层速度结构.对于本文方法，采用第2.3节理论算例中相同的反演参数，将遗传代数取为200，每一遗传代的个体数为200，GA操作中代沟值为0.9，交叉率为0.7，变异率为0.01，SA的初始温度设置为10℃，SA温度衰减系数C0为0.99.当遗传代数达到200代时，反演过程自动结束，得到与最小目标函数相对应的反演模型即为最佳反演模型.对于HV-Inv法反演，首先采用全局的Monte Carlo抽样，迭代次数设置为100，扰动范围设置为10%(此值控制当前模型周围的最大扰动范围，在此范围内产生下一个模型)，而后采用修正的模拟退火(Modified SA)，其初始温度设置为6.0℃，温度衰减系数C0为0.9，当遗传代数达到500代时，反演过程自动结束，得到与最小目标函数相对应的反演模型即为最佳反演模型.反演过程中不同方法的目标函数随迭代次数的变化曲线如图13所示，由该图可知本文方法收敛速度远快于HV-Inv方法，反演经100代之后本文方法的反演结果即趋于稳定.图14给出了不同方法反演的模型与钻孔数据的比较.VP、VS、h随迭代次数的变化情况示于图15，限于篇幅，仅给出了第一层土体参数的结果，该结果能清晰地显示反演参数随迭代次数增大快速收敛至最佳值的过程.我们也很容易注意到图15所示的土层厚度并不随迭代次数增加而变化，这主要是因为缺乏约束土层厚度的信息，将土层厚度取为了固定值.两种反演方法获得的最佳拟合模型示于图14中，将表5所示的钻孔模型采用等效波速法折算到相应层厚作为反演结果的参照.由该图可知，两种反演方法获得的四层土体速度结构模型总体上与钻孔揭示的速度结构较为接近，本文方法相比HV-Inv方法能更准确地获得基岩层剪切波速.对第一和第三层土体的波速不同方法的反演结果接近，且与钻孔数据较为接近，对第二层土体本文方法与钻孔数据的差别要远小于HV-Inv方法且反演结果与钻孔数据十分接近.图12给出了反演模型对应的NHV曲线对目标曲线的拟合结果，该结果表明本文反演模型能很好地拟合目标曲线，反演模型可视为更符合地表观测结果的土体等效速度结构模型，其模型参数的不确定性可用表6中的方差来描述.

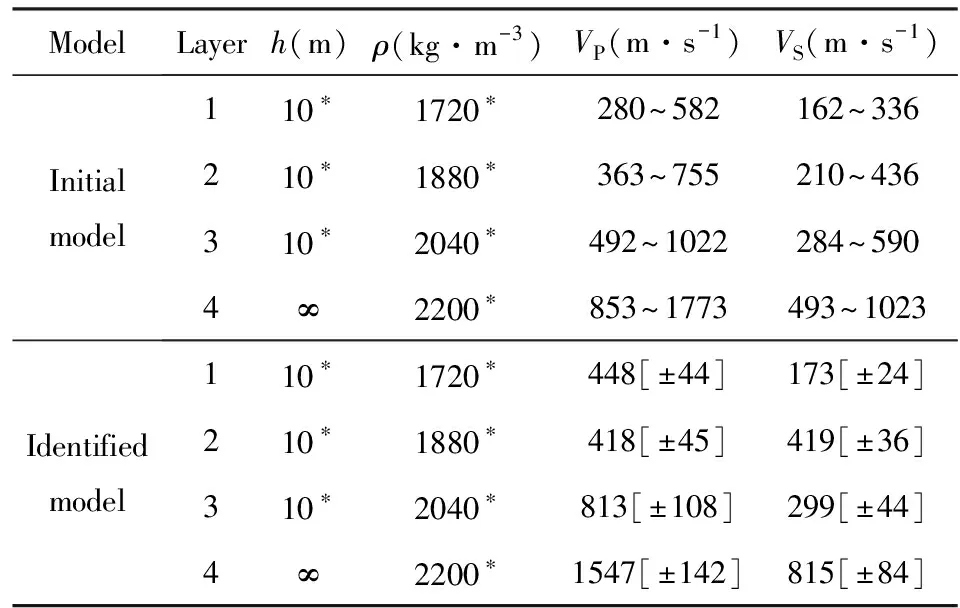
表6 初始模型和反演模型

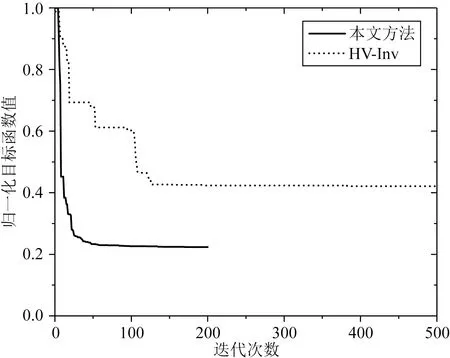
图13 归一化目标函数随迭代次数的变化曲线

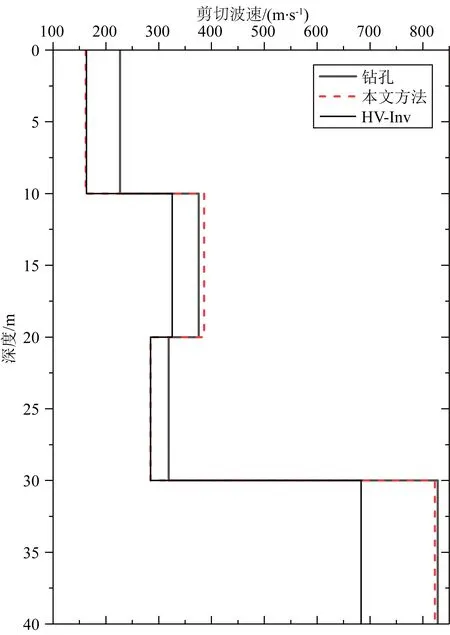
图14 不同方法反演的最佳模型及与钻孔数据的比较

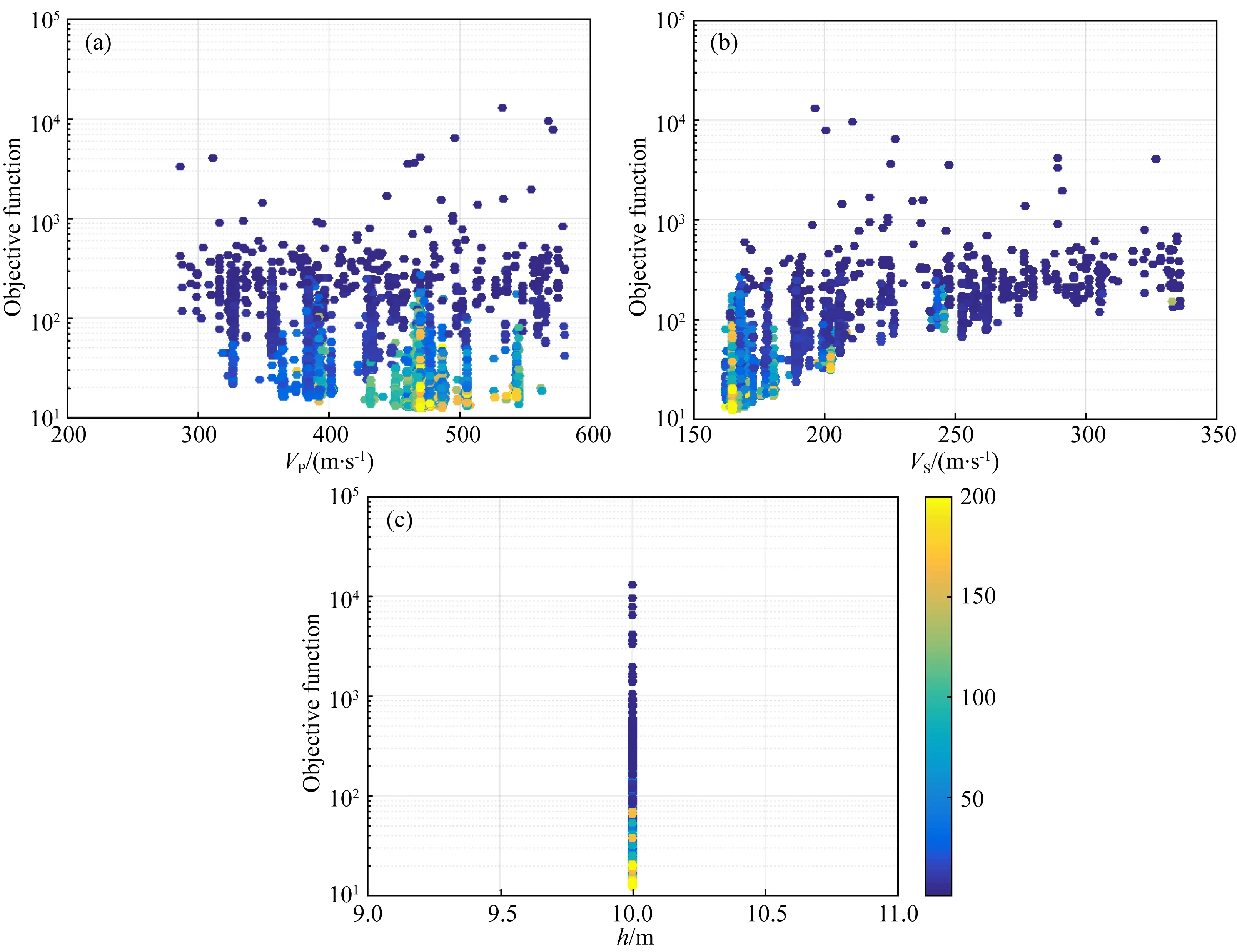
图15 参数随迭代次数变化

综合图12—15的结果我们可以看到，无论是采用本文方法还是HV-Inv方法，反演过程本质上都是使得反演模型的NHV曲线不断趋近目标NHV曲线的过程，而目标NHV与钻孔模型的理论NHV在幅值和频谱上本身就有一定差别(如图12)，从这个角度来看，反演得到的最佳模型与钻孔有差别属于正常现象，钻孔数据仅能作为反演结果的参照，但从图11揭示的结果，将该场地视为一维场地是合理的，钻孔在很大程度上能较好地代表背景噪声台站布设的场地特征，因此反演模型与钻孔越接近表明反演效果越好，图14的结果恰好证实本文反演方法的效果要优于已有的HV-Inv方法，尤其对于岩土分界面的揭示及基岩剪切波速的确定，本文方法更有明显的优势.

4 结论

场地土层是各类工程建设极为关注的近地表介质层，利用地表观测的背景噪声反演场地土层速度结构的研究仍较少.本文将已有的遗传模拟退火混合算法与基于散射场假定的NHV正演计算方法相结合，提出了一种基于背景噪声波场NHV反演场地土层速度结构的全局反演方法，通过简化模型的参数敏感性分析，揭示了场地土层的VP、VS及厚度是影响场地地表NHV的主要因素，而密度参数的影响几乎可以忽略.理论算例验证了本文全局反演方法的可靠性.随后本文利用唐山响嘡竖向台阵场地的背景噪声观测获得了面波频散曲线，为土层速度结构反演提供了初始模型信息.基于该初始模型，采用本文反演方法获得了较为接近钻孔测井数据的地下速度结构.

理论和实际应用算例以及与同类方法的比较均表明本文方法是基于地表背景噪声观测反演场地土层速度结构的合理、可靠的方法，可为近地表土层模型参数的确定提供一种低成本且有效的途径，但由于土层速度结构的背景噪声反演研究尚处于起步阶段，目前反演获得的土层速度结构的细致程度仍取决于与面波频散曲线相关的初始模型的精细程度以及地表NHV曲线的频段范围，这方面的研究仍有大量基本问题如模型参数对背景噪声波场的影响规律、反演模型的分辨率及其不确定性评价等都亟待解决，对于这些问题尚需进一步开展更深入的研究工作.