Asymmetric coherent rainbows induced by liquid convection∗

Tingting Shi(施婷婷) Xuan Qian(钱轩) Tianjiao Sun(孙天娇) Li Cheng(程力)Runjiang Dou(窦润江) Liyuan Liu(刘力源) and Yang Ji(姬扬)

1State Key Laboratory for Superlattices and Microstructures,Institute of Semiconductors,Chinese Academy of Sciences,Beijing 100083,China

2College of Materials Science and Opto-Electronic Technology,University of Chinese Academy of Sciences,Beijing 100049,China

3College of Physical Sciences,University of Chinese Academy of Sciences,Beijing 100049,China

4Center of Materials Science and Optoelectronics Engineering,University of Chinese Academy of Sciences,Beijing 100049,China

Keywords: coherent interference,thermal lens effect,convection,numerical simulation

1. Introduction

Coherent rainbows are colorful interference rings formed by injecting white laser into liquids or solids. It has been observed in pure solvents (e.g., water, acetone, and anhydrous ethanol),plastics,wax and ice.[1–3]Interference rings induced by single-wavelength lasers were reported much earlier (e.g.,liquid crystals,[4–6]tea,[7]nano-material suspensions,[8–18]and organic solvents).[19,20]There are mainly two models to explain interference rings in liquids: the thermal lens effect[8,16,19]and the electronic third-order nonlinear selfphase modulation.[9,10,12,14,17]While different materials and models were used in these studies, the asymmetric shapes of the interference rings (when appeared) were ascribed to convection,but no detailed discussion was given. Here we report experimental study of the effect of convection on the shape of interference rings. We also clarify the mechanism behind the coherent rainbows in the liquid. The optical path difference necessary for the interference comes from the local change of the refractive index,which in turn comes from the temperature distribution in the liquid induced by laser heating. The liquid behaves as a non-ideal plane concave lens, i.e., the thermal lens effect. When the temperature of the liquid in the middle part of the laser beam becomes much higher than that of the outer part, convection occurs in the upper part of the liquid,while the lower part stays still. This makes the temperature distribution in the liquid asymmetric (an up–down asymmetry),thus leading to the asymmetric interference rings.We also numerically simulate the effect of heat conduction on the temperature distribution in the liquid in two-dimensional cases,with and without convection, respectively. The numerical results agree well with our experimental observations.

2. Experimental systems and observations

2.1. Experimental setup

The experimental setup is shown in Fig. 1. A fiber laser with white light pulse is used(Model: SC-PRO,Wuhan Yangtze Soton Laser Company). Its wavelength ranges from 400 nm to 2400 nm,with a pulse width∼100 ps,a beam diameter∼2 mm(@633 nm),and an emission angle<1 mrad.The repetition rate is 1 MHz and the visible light power is continuously adjustable from 0 to 1 W.When the shutter(SH)is opened, the white laser (WL) beam from the fiber laser is focused through the lens (L) into the sample (S), and colorful interference rings(coherent rainbows)appear on the image screen(IS),an interference filter(IF)can be inserted into the laser beam,just behind the sample. The free-fall part(FF,enclosed by the dash line)has all the components fixed to a stage and we can let it go a free-fall. The focal length of the lens is about 10 cm,the sample is placed in a quartz cuvette,and the distance between the imaging screen and the sample is about 30 cm. The optical path is 10 mm in the liquid. Colorful images are recorded with a commercial cell-phone,and blackwhite images are recorded with a high-speed camera, which can capture 1000 frames per second with an image resolution of 800×600 pixels.[21]

Fig.1. Schematic diagram of the experimental set-up: when the shutter(SH)opens,the white laser(WL)beam from a pulsed fiber is focused through the lens(L)into the sample(S),and the colorful interference rings(coherent rainbows)appear on the image screen(IS).An interference filter(IF)can be inserted behind the sample. The FF part(enclosed by the dash line)is fixed to a stage and we can let it go a free-fall.

2.2. Experimental materials

Samples are water and/or dimethicone. Dimethicone is a kind of hydrophobic silicone material, also known as polydime-thylsiloxane. It has a wide range of molar mass(162–500000 g/mol),with viscosity varying from 0.65 mm2/s to 1000000 mm2/s. By adjusting the amount of chain stopper during synthesis,or mixing two kinds of dimethicone with different viscosity,one can obtain dimethicone with any specific viscosity.[22]The viscosity of dimethicone used in the experiment is 50 cst, 500 cst, 5000 cst, and 50000 cst, respectively(1 cst=1 mm2/s). The viscosity of water is about 0.89 cst at room temperature.

2.3. Experimental results

Multi-order colorful rings are observed in water and dimethicone with various viscosity, as show in Fig. 1 for the case of water. To make observation and analysis easier, we insert an IF (central wavelength 632.8 nm, half width of full magnitude 10 nm±2 nm)behind the sample and record blackand-white images with the high-speed camera, as shown in

Fig. 2. The interference rings of water (Fig. 2(a)) have an oval shape, with the distance between rings becoming wider and wider from the center to the edge. Obviously they are asymmetric, i.e., instead of concentric circles, they are oval with a core sitting in the upper part. The interference patterns from dimethicone with viscosity 50 cst,500 cst,5000 cst and 50000 cst are shown in Figs.2(b)–2(e). They are much bigger than that from water. The interference rings from the dimethicone with viscosity 50 cst (Fig. 2(b)) deviate from the circular symmetry most significantly, similar to water shown in Fig. 2(a). With the increase of the viscosity, the shape of the rings gradually changes from oval ones to circular ones. As for the dimethicone with viscosity 50000 cst,the shape of the interference rings is almost circular(Fig.2(e)).

After the shutter opens, we record the dynamics of the interference rings with the high-speed camera mentioned before. It takes much shorter time for water to form a stable oval shape than the dimethicone. We choose water as the sample in the following dynamic experiments, though the results of dimethicone are similar. The laser beam goes in the horizontal plane. As shown in Fig. 3(a), concentric circles start to appear when the shutter opens. Then the rings gradually spread out and the number of rings increases. The number of the rings reaches the maximum at∼0.08 s, and the interference rings distort more and more and reach a stable oval shape after∼0.20 s. When the white light goes perpendicularly,along the direction of the gravity,there are only a set of concentric circles.[1]This suggests that the asymmetric rings are caused by the convection in the liquid. To check it,we let the FF part go a free-fall and open the shutter simultaneously.As shown in Fig. 3(b), the interference rings also spread out(and the number of rings increases,too),however,their shape remains circular. When the shape of the interference rings is stable in static state, we reduce the laser power from 1 W to 0.6 W in less than 1 ms,the shape of the rings will remain the same,but the intensity of the rings will drops(Fig.3(c)).After a few milliseconds(ms),they begin to shrink inward,and the number of rings decreases gradually.

Fig.2. Interference rings from(a)water,(b)–(e)dimethicone with different viscosity.

Fig.3. Dynamic of the interference rings from water: (a)in static state,(b)in free-fall. (c)In static and stable state,the laser power is reduced from 1 W to 0.6 W in less than 1 ms.

3. Theoretical analysis and numerical simulation

Multi-order colorful interference rings in the liquid come from the change of local refractive index for sure. The controversy lays on which mechanism induces the refractive index change. Wuet al.explained it with electronic thirdorder nonlinear self-phase modulation and proposed a windchime model to account for the emergence of the ac electron coherence.[17]Many others took the thermal lens effect as the mechanism,such as Pillaet al.,[8]Wanget al.[16]and Zhanget al.[19]They ascribed the optical path difference to the temperature gradient in the liquid. However,the effect of convection in the liquid has not be discussed in details,though it has been mentioned before.[4,9–11,14,16–18]Here we clarify the formation mechanism of interference rings in the liquid with and without convection,respectively.

We make a gross assumption that the laser heating of liquid along the laser direction is uniform in a finite lengthlnear the focal point. In other words,we only consider the thermal conduction perpendicular to the laser propagation direction.In this way,the three-dimensional problem is transformed into a two-dimensional one,which greatly simplifies our subsequent theoretical analysis and numerical simulation.

The laser heating process of the liquid can be divided into two stages. In the first stage, the liquid at room temperature is suddenly irradiated by laser. The temperature rises continuously,but the temperature gradient is not big enough to start convection in the liquid. In the second stage, as the heating goes on,the temperature of the liquid in the middle part of the laser beam becomes much higher than that of the outer part,and convection is generated and it affects the heat conduction.

3.1. The first stage: no convection

First,we consider the case without convection. When the Gaussian-shape laser beam is absorbed,the local temperature goes up. The heating process of liquid can be expressed by the following heat conduction equation:

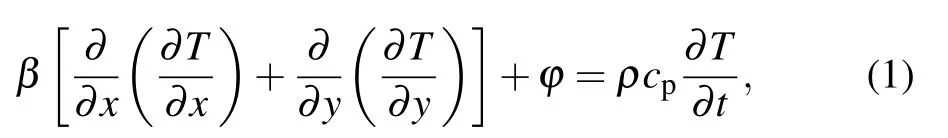
whereβis the thermal conductivity coefficient;x,yare the coordinate axes;the planexoyis perpendicular to the laser direction;ϕis the heat flux density;ρis the density of the liquid;cpis the constant pressure specific heat capacity of the liquid;andtis the time.

This is a typical thermal conduction process. The refractive indexnchanges accordingly, since the latter is inversely proportional to temperature for most media. The higher the temperature is,the smaller the refractive index is. Figure 4(a)shows the two-dimensional distribution of refractive index in the planexoy. Black circle indicates the Gaussian-shape laser spot, and its beam waist radiusw0is 100 µm in the simulation. The distribution of refractive index remains unchanged in the direction of laser beamz,so the optical-path difference∆ℓ=∫∆ndlpassing through the liquid also shows a bump shape when ∆nx=nx −nx=0, as shown in Fig. 4(b). In other words, we regard the optical-path difference at the center of the beam as zero, and then normalize the optical-path difference at each position, with laser wavelengthλ=632.8 nm.Figure 4(c)shows the radial gradient of the optical-path,which determines the outgoing direction of each sub-beamφ. The highest point corresponds to the maximum outgoing angle(i.e.,the outgoing direction),which determines the size of the outermost ring.[3]When the outgoing angle is smaller than its maximum value,there are two sub-beams going into the same direction(φr1=φr2),whose optical path difference can be expressed ass=(∆ℓr1−∆ℓr2)−(r1−r2)·φin far-field regime.They may interfere constructively or destructively,depending on the optical-path differencesbetween them. The constructive(destructive)interference occurs whens/λ=mkπfor integermbeing even(odd). As the liquid temperature increases,the maximum optical path difference and the maximum outgoing angle also increase. The radial distribution of interference rings may be simulated,as shown in Figs.4(d)and 4(e).The rings are dense at the center, and become sparser as the outgoing angle increases,in agreement with the experimental observations.

Fig.4. Formation mechanism and numerical simulation of interference rings without convection. (a) The two-dimensional distribution of refractive index in the plane xoy. Black circle indicates the Gaussianshape laser spot, and its beam waist radius w0 is 100 µm in the simulation. (b) The distribution of optical path difference ∆ℓ along the radial direction. (c) The radial gradient of the optical path difference. Two sub-beams at r1 and r2 are refracted into the same angle φr1 = φr2, whose optical path difference can be expressed as ∆s =(∆ℓr1 −∆ℓr2)−(r1 −r2)·φ in far-field regime. The constructive (destructive)interference occurs when s/λ =mkπ for integer m being even(odd). (d), (e) The radial distribution of interference rings obtained in the planes xoy and xoz by simulation,respectively.

3.2. The second stage: convection starts

As the heating goes on,the temperature difference of the liquid reaches a threshold, and convection starts. This is a result of Rayleigh instability which relates to the thermal gradient,the gravity and viscosity of the liquid. It is worth noting that convection occurs in the upper part of the liquid, while the lower part stays still. The reason is the following. With the laser beam being the center,from the center to the upper outmost part,the temperature is lower and lower,i.e.,the density becomes heavier. This results in buoyancy which can oppose gravity and viscosity of the liquid,thus leading to convection.In the lower half, no convection occurs since the temperature gradient is along the direction of the gravity. This leads to an asymmetric temperature distribution in the liquid,and thus the asymmetric interference rings. The higher the viscosity of the liquid is,the stronger the internal friction is in the flow,and it is more difficult to start convection. This is why the shape of the interference rings changes from oval ones to circular ones as the viscosity increases,as shown in Figs.2(b)an 2(e).

The dynamic experiment (Fig. 3(a)) also proves that the asymmetry comes from the convection. After the injection of the laser, but before the convection starts, heat conduction is symmetric and circular-shape rings are observed.As time goes by,convection starts. Accordingly,a non-circular temperature distribution forms, which turns the circular shape of the interference rings into an oval shape. When the FF part makes a free-fall, the convection cannot start, since the gravity does not act on the liquid(“weight-loss”).So,the interference rings remain circular(Fig.3(b)).

For the convenience of calculation,we may regard the effect of the convection as an additional thermal conductivity∆β. As shown before,the convection exists only in the upper half of the perpendicular plane. In other words, the effective thermal conductivity of the upper part is larger than that of the lower part, as shown in Fig. 5(a). The heat-conduction convection differential equation is the following:

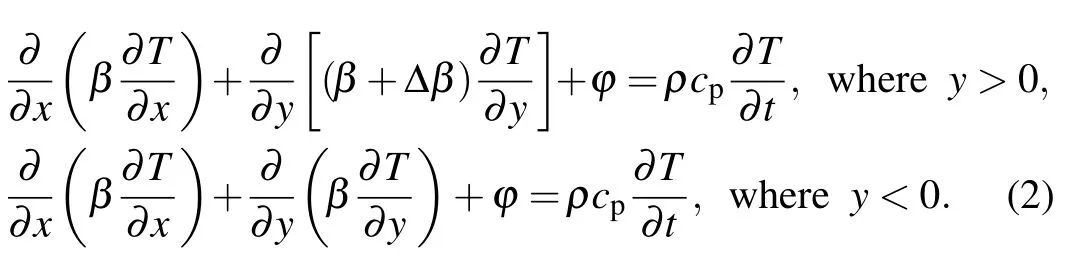
Because of the additional thermal conductivity ∆β,the refractive index distribution (temperature distribution) of the upper half plane is less dramatic than the lower half, in other words, the refractive index gradient (temperature gradient) is smoother, as shown in Fig. 5(b). The maximum value of the gradient is smaller,i.e.,the outgoing direction of the maximum ring decreases. Therefore, the shape of the interference rings is an oval with a small top and a big bottom. The fitting result verifies the theoretical explanation,as shown in Fig.5(c).This also explains why the size of interference rings from water is smaller than that from dimethicone. Table 1 shows some thermophysical parameters of water and dimethicone.The thermal diffusivityK=β/ρcp,which describes the diffusion ability in the process of heat conduction,of water(∼1.5×10−7m2/s)is 1.5 times that of dimethicone(∼1.0×10−7m2/s). The power of the incident light is the same, but the absorptivity of water is greater than that of dimethicone,of water is just 1.5 times that of dimethicone. So according to Eq.(1), when the steady state is reached(∂T/∂t=0),the temperature gradient of water and dimethicone is the same. The refractive temperature coefficient of water is−1.37×104K−1, while that of most liquid organic compounds is from−3×104K−1to−5×104K−1,[23]thus the maximum optical path difference gradient (the maximum outgoing angle) of water is smaller than that of dimethicone. So the size of the interference rings from water is smaller. Besides that,because the thermal conduction of water is greater than that of dimethicone, this explains why the time for water to reach steady state is shorter than that of dimethicone(∼0.20 s and∼2 s,respectively).

Fig. 5. Formation mechanism and numerical simulation of interference rings with convection. (a) Equivalent model of heat convection. (b)The distribution of refractive index in the plane xoy. (c)The radial distribution of interference rings obtained by simulation.

Table 1. Thermophysical parameters of water and dimethicone.

In addition, when the laser power is reduced suddenly,the temperature distribution in liquid remains unchanged(for a few ms),so the interference pattern does not change,as shown in Fig. 3(c). In other words, its response time is longer than 1 ms. This also suggests that the mechanism behind the interference rings is a thermal effect—the response time of refractive index change caused by thermal effect is about 10−3–1 s,while the response time of other effects is much shorter (for instance, the high frequency Kerr effect related to polarized molecules is about 10−11–10−12s).[24]All in all,the above experiments have confirmed that the asymmetry of interference rings is due to the convection,along with a local change of the refractive index induced by laser heating(thermal lens effect).

4. Discussion and conclusion

Focus a white light laser on different viscosity of dimethicone,different shapes of interference rings will appear. Increase the viscosity,the shape of the interference rings changes from oval to circular shape. When the liquid is free-fall, the interference rings remain symmetrical. The reason for the formation of interference rings is that the temperature distribution in the liquid changes due to laser heating, which affects the refractive properties and leads to optical path difference. The symmetry of the rings is caused by the convection, which makes the temperature distribution asymmetric.The two-dimensional heat conduction simulation is consistent with the observation results, thus verifying the rationality of the physical mechanism.