基于逆算子估计的AVO反演方法研究

印兴耀, 邓炜, 宗兆云

中国石油大学(华东)地球科学与技术学院, 山东青岛　266580

基于逆算子估计的AVO反演方法研究

印兴耀, 邓炜, 宗兆云

中国石油大学(华东)地球科学与技术学院, 山东青岛266580

摘要传统反演算法以优化算法为主，而基于逆算子估计的AVO反演算法则利用了直接求逆的思路.算法的关键在于寻找存在逆函数的子域，进而可以在子域内直接求逆，这种解决反问题的思路不同于一般的优化类算法所采用的直接搜索解的方式，具有更高的效率.AVO反演利用了振幅随着偏移距的变化特征，反演的精度受到地震资料质量的影响，通过加入L1范数约束以及合理的初始模型有助于提高反演的稳定性以及准确度.模型测算和实际应用表明，基于逆算子估计的AVO反演方法具有较高的精确程度和可靠性.

关键词AVO反演； 逆算子估计； L1范数； 初始模型

Aki&Richards approximation is utilized to establish the inversion objective function. L1 norm constraint is considered on the basis of reasonable initial model in order to improve effciency and stability during AVO inversion process. Inverse operator estimation algorithm utilizes numerical approximation of objective function in empirically constrained subspaces. The existence of inverse mapping inside these subspaces is supposed, and thus the existence of its numerical approximation is also supposed. This numerical approximation is used for the prediction of the solution. It can be divided into the following four steps: (1) initialization, (2) selection, (3)prediction,(4) solution space correction. Since this method is approximate, the algorithm is arranged into iterative cycles and the solution is gained successively.

Model test in which noise immunity and stability based on L1 norm constraint are considered lays the foundation for the actual data inversion. In the model test, the inversion results based on synthetic seismogram with different SNR noise remain good consistency with the model value. L1 constraint is necessary, a relatively stable result can be obtained in multiple inversion processes and it helps reduce the number of singular values. The seismic data is from China′s land, inversion quality can be evaluated by well data and seismic data.Inversion results of actual seismic data maintain good consistency with logging curves.

Reliability of the solution, noise immunity and convergence speed can be improved by increasing the constraint requirements and considering reasonable initial models. Poor lateral continuity when dealing with actual data can be reduced by optimizing the objective function and the initial model. In general, AVO inversion based on inverse operator estimation is effective and potential.KeywordsAVO inversion； Inverse operator estimation; L1 norm; Initial model

1引言

叠前弹性参数反演是利用叠前地震信息、测井资料数据以及地质信息反演地下的相关参数、预测储层以及流体(杨培杰和印兴耀，2008;印兴耀等，2010,2014)的一种方法.相比于叠后反演方法，利用AVO反演方法可以更为精确地提取反映岩石含油气性以及岩性的属性参数(Goodway et al.,1997;Gray and Andersen,2001; Xingyao Yin and Shixin Zhang，2014；Zong et al.,2015;Yin et al.,2015)，从而提高流体识别和储层预测的精度.

基于逆算子估计的AVO反演方法是根据Zoeppritz方程近似式(Bortfeld，1961；Aki and Richards,1980; Shuey,1985;郑晓东,1991；Zong et al.,2012，2013a )直接求取三参数的方法，利用Aki&Richards近似方程建立反演方程，目标函数为正演数据与观测数据残差的L2范数，由于反演问题的不适定性，较小的噪声即可对反演结果带来较大影响，可以通过正则化改善反演结果(Tikhonov,1963)，因此本文在L2范数基础上加入L1范数以及初始模型(宗兆云等，2012,2013b;Yin et al.,2013)进行约束.求解过程中逆算子估计算法的精确程度和稳定性至关重要，通过试验表明算法可以稳定地提取三参数信息.逆算子估计算法在实现过程中最重要的是找到存在逆函数的区域，继而在这些区域内直接求逆，并且在每一次求解中循环利用线性回归、径向基函数网络和克里金3种不同方法，增强了对于反问题的适应性.

本文首先阐述了基于逆算子估计的AVO反演方法的理论基础，包括反演目标函数构建以及目标参数求解过程，然后分别利用模型测算和实际资料应用验证方法的可行性以及有效性.在模型测试部分除了进行抗噪性测试，还考虑L1范数约束以及初始模型对反演的影响.实际应用部分则利用实际资料直接反演得到三参数信息，并验证其合理性.

2理论基础

2.1反演方程

1980年Aki和Richard整理了Frasier和Richards的研究成果，提出了Zoeppritz方程的近似式，即用纵横波反射系数以及密度反射系数表示的线性近似式：

(1)

其中，

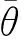
(2)

其中，Rp,Rs,Rd分别代表纵波速度反射系数、横波速度反射系数以及密度反射系数.利用正演模型我们可以得到某一个采样点不同角度的反射系数，原则上我们只需要3个角度的信息就可以达到目的.建立如下所示的目标函数：

(3)

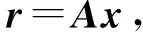
(4)

(5)

(6)

参数向量代表待求参数，数据向量代表观测数据，误差代表精度，精度表示形式为

算法实现包括4个步骤，初始化、选择、预测、校正.初始化阶段需要定义求解范围、模型向量和数据向量的维数；选择最为关键，目的在于在一个较大的空间内寻找到存在逆函数诸多的小空间；预测则是在这些空间内求解，可以通过很多方法求解，本文中采用线性回归、径向基函数网络(阎平凡和张长水,2005)、克里金3种方法.实验证明3种方法在算法循环的过程中的循环利用可以有效地提高算法的精度和适应性；在校正阶段则使求得的解更加合理，即使得目标函数最小.算法在上述步骤的不断循环中实现.

(1) 初始化

在这个阶段，对各个必要的参数进行初始化，下一次的计算参数要被限制在已定义的空间内部.

初始模型的集合是按照统一的概率分布在既定的空间内.所有的模型按照误差的大小排序，误差最小的称为Mb:

Mb={pb,db,errb},errb=min(erri),

i=1,2…q.

(7)

在每次的迭代中产生的每个模型集合都要按照特定的几何规则分布：先选择一个模型并且作为集合的中心，其他的q-1个模型随机地分布在以其为圆心、R为半径的球体或者超球体面上.

(2) 选择

第一次循环前，随机选择集合中心pc,且R=1.假设{pc,R}已知，将按照下列步骤产生新的预测模型：

1) 集合的中心模型{pc,dc,errc}作为第一个模型；

2) 张量Cm以Choleski分解Cm=LLT；

3) 候选模型pg=pc+R Lg；

g为单位向量.根据合理的条件判断该模型是否合理，为了提高算法的效率，在选择预测模型的时候如果产生了与之前的模型非常靠近的情况，那么就不应该被选择，这样就减少了需要正演评估的计算量.

(3) 预测

被选择的预测模型在这个阶段{pi,di,erri},i=1,2…q才是可以利用的：预测模型集合{pi,di,erri}→预测算法→候选解p0.

实验表明，在复杂多样的环境下只使用相同的预测算法不利于提高算法的适用性，最好的方式是：即使是在一个单一的求逆过程中都要利用多种预测算法.现在逆算子估计是利用3种预测算法：线性回归；利用RBFN(径向基函数网络)预测和“克里金”.

通过选择，可以保证在新的模型空间内逆函数存在，3种算法的循环使用对一个未知的反问题有更强的适应性.

(4) 校正

预测的质量原则上可以通过对下列事项的考虑来控制：1) 组成集合的个体的个数q；2) 集合的大小，即直径R；3) 集合的位置，即集合的中心pc.

模型个数q会影响计算量，q值越大，需要选择的模型越多，计算量就会增大，但是对结果的影响较小，q值是随着迭代次数的增加不断自动发生改变的，如果要求更高的精度选取较大的q值是有利的，一般选取范围为模型参数个数的3～5倍.校正的关键在于集合的大小以及集合的位置，具体的校正方法如表1所示，其中nwait表示在循环过程中误差没有改善的循环次数.可以看到目的就在于使得误差err越来越小.

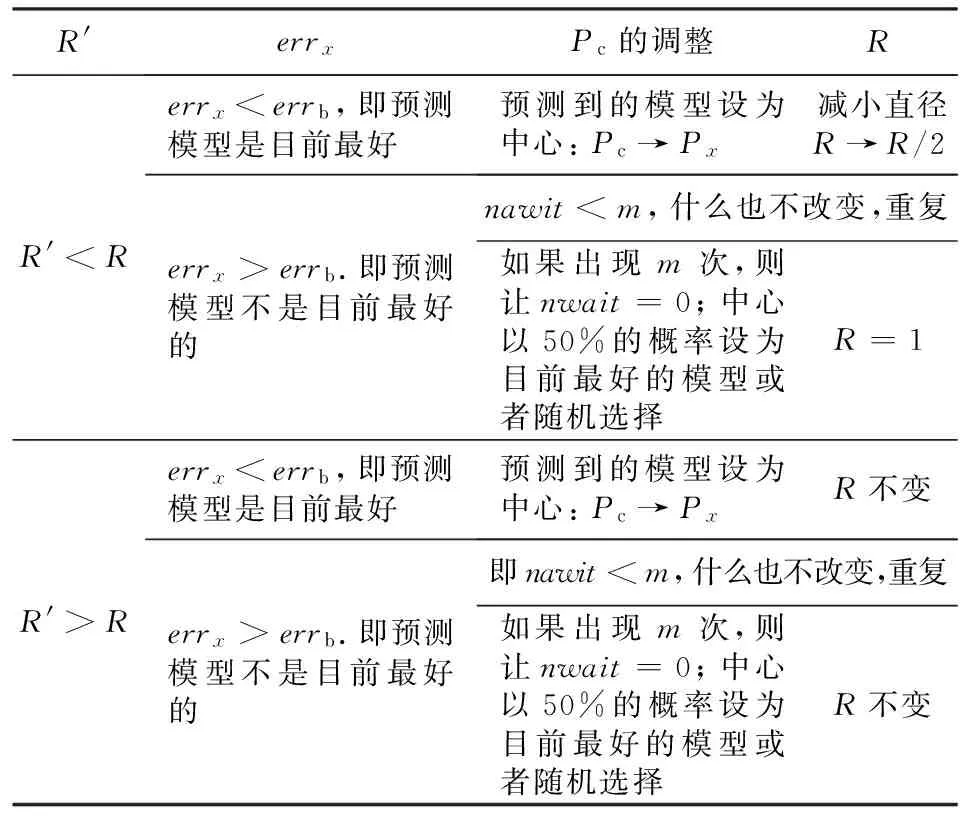
表1　校正方法表

3模型反演

下面是一个实际的井资料模型，包括横波速度、纵波速度以及密度反射系数.三参数模型值如图1所示.

图1　井模型参数图(a) 纵波速度反射系数； (b) 横波速度反射系数； (c) 密度反射系数.Fig.1　Well model parameters(a) P-wave velocity reflection coefficient; (b) Shear wave velocity reflection coefficient; (c) Density reflection coefficient.

利用模型数据以及主频为40 Hz的雷克子波合成地震记录，反演得到如图2所示的结果，其中蓝色为反演值，红色为模型值，青绿色为初始值，可以看到反演值与模型值保持很好的一致性，初始值为模型值的100次平滑，初始值与模型值的相关性不高，但是反演结果仍然理想.

给合成记录加信噪比为3的噪声，合成记录加噪声前后对比如图3所示((a)为未加噪声合成记录，(b)为加噪声记录)，对密度项的反演结果较其他两项较差，初始值较不加噪声反演的时候与模型值的相关性提高一点，但反演结果与模型值也保持了很好的一致性.图4为加信噪比时反演结果与模型值对比.

给合成记录加上信噪比为1的噪声，合成记录加噪声前后对比如图5所示((a)未加噪声，(b)为加噪声)，图6为反演结果.从图4和图6可以观察到，随着噪声增加，反演对初始模型的依赖性相应增加.

初始模型是对模型的不同程度的多次平滑，约束解的范围是在初始模型基础上加减一个该参数的最大值或者最小值.从模型测试的结果可以看出，无噪声时，反演结果与模型值有很高的吻合度，对初始模型的依赖较低，加入不同程度信噪比噪声后反演结果与模型值也保持了较好的吻合度，但是对初始模型的要求也相应有所增加，更好的初始模型有助于得到更好的反演结果.从3个测试的结果可以看到，对于密度的反演结果相对较差，这也是目前线性反演研究工作的一个难点，并非单纯只是本文所使用的算法的原因.从图2可以看出在资料信噪比较高的情况下对初始模型的依赖性不强.如果资料的信噪比较低，除了寻找更加合适的初始模型之外，还可以通过提高精度要求和循环次数来改善反演结果.总体来说，算法有较高的准确度和稳定性，但是对于密度项的反演结果较其他两项差一点.

由于本文采用的是一种新的非优化算法，所以对于加入L1范数以及初始模型是否对于反演有帮助是值得商榷的，因此笔者比较了不加范数和模型与加范数和模型两种情况的反演结果.

考虑到的影响主要分为两个方面：稳定性和反演中奇异值数量.

为了验证加约束项对于结果稳定性的影响，在信噪比为2的情况下，对上述的反演过程独立进行10次，将3参数信息利用道积分方法转换成密度、纵横波速度信息，得到10个反演结果.对于每一个采样点，计算这10次反演结果与模型值的方差以及所有采样点方差的总和的平均，得到表2，然后分别作归一化处理得到图7，从左至右分别是纵波速度方差、横波速度方差和密度方差，为了得到一个趋势笔者做了一定的平滑处理.值得注意的是，由于做了归一化，图7上的大小只是相对的，不能说明两者的绝对大小，绝对大小如表2所示.

图2　反演结果与模型值对比图红色曲线代表模型值，蓝色曲线为反演值，青绿色曲线为初始值. (a) 纵波速度反射系数反演结果比对； (b) 横波速度反射系数反演结果比对； (c) 密度反射系数反演结果比对.Fig.2　The comparison between inversion results and the model valueThe model value is colored with red.The inversion value is colored with blue and the initial value is colored with green.(a) Inversion result of P-wave velocity reflection coefficient; (b) Inversion result of shear wave velocity reflection coefficient; (c) Inversion result of density reflection coefficient.

图3　加噪声(信噪比为3)前(a)后(b)合成记录对比图Fig.3　The comparison of synthetic seismogram (S/N=3)

图4　合成记录加信噪比为3时噪声反演结果与模型值对比图红色曲线代表模型值，蓝色曲线为反演值，青绿色曲线为初始值. (a) 纵波速度反射系数反演结果比对； (b) 横波速度反射系数反演结果比对； (c) 密度反射系数反演结果比对.Fig.4　The comparison between inversion results and the model value with S/N=3The model value is colored with red.The inversion value is colored with blue and the initial value is colored with green. (a) Inversion result of P-wave velocity reflection coefficient; (b) Inversion result of shear wave velocity reflection coefficient; (c) Inversion result of density reflection coefficient.

图5　加噪声(信噪比为1)前(a)后(b)合成记录对比图Fig.5　The comparison of synthetic seismogram (S/N=1)

图6　合成记录加信噪比为1噪声反演结果与模型值对比图红色曲线代表模型值，蓝色曲线为反演值，青绿色曲线为初始值. (a) 纵波速度反射系数反演结果比对； (b) 横波速度反射系数反演结果比对； (c) 密度反射系数反演结果比对.Fig.6　The comparison between inversion results and the model value with S/N=1 The model value is colored with red. The inversion value is colored with blue and the initial value is colored with green. (a) Inversion result of P-wave velocity reflection coefficient; (b) Inversion result of shear wave velocity reflection coefficient; (c) Inversion result of density reflection coefficient.

图7　加约束项与初始模型前后稳定性对比红色曲线为不加约束和初始模型，蓝色代表加入约束项以及初始模型. (a) 纵波速度误差； (b) 横波速度误差； (c) 密度误差.Fig.7　Stability with constraint term and the initial model compared to the condition without it The error with constraint and initial model is colored with blue. The error without them is colored with red. (a) Error of P-velocity; (b) Error of shear wave velocity; (c) Error of density.

图8　合成10°、20°、30°地震记录以及反演剖面Fig.8　Synthetic seismograms and P-wave velocity, shear velocity, density inversion results

由表2可以得到，加了约束项和模型后方差总和整体上明显小于不加约束项，说明整体上稳定性有所提高.平均误差为方差，反应了与模型值的差值绝对值，可以看到加L1约束以及模型后误差明显减小.再观察图7，红色曲线代表未加约束项与模型，蓝色代表加约束项与模型，对于每一个采样点来说，未加约束项和模型的纵波速度的方差变化幅度为0.3～1，而加了约束项和模型的则基本维持在0.5附近，结合表2不难看出，加了约束项和模型后对于每一个采样点而言误差是相对较小的，并且从整体上来讲误差维持在一个更加稳定的水平.同样对于密度有类似的现象.综上所述，加入合适的约束项和模型后有利于提高结果的稳定性.

表2　方差总和数值表

其次是所耗时间，对10次反演过程经过统计，300个采样点平均在反演过程中由于奇异值存在而使得算法无法在既定的有限循环次数内达到求解精度的平均次数为12，而加入约束和初始模型后平均次数为3，所以时间有大幅度减少.

综上所述，算法可以通过加入L1范数与初始模型来提高稳定性以及计算效率.

对于二维剖面模型，在不加噪声的情况下，合成10°、20°、30°的地震记录(图8a).选取的初始模型是对每一道数据进行100次平滑，反演得到如下纵波速度、横波速度以及密度剖面如图8b所示(从左自右).

二维模型反演的目的在于验证横向连续性.从二维模型的反演结果看，算法具有较高的分辨率，横向连续性较好，说明在得到高准确度的反射系数或者子波后逆算子估计算法具有很高的准确性，这也为处理实际资料打下理论基础.

4实际应用

实际地震数据来自中国大陆陆地某勘探工区.图9为3个部分角度叠加剖面，图9依次分别是小角度(中心角度10°)、中角度(中心角度20°)、大角度(中心角度30°)的剖面，一共70道，采样间隔为2 ms.在该工区提取3个角度的地震子波，加入L1范数约束以及适当的初始模型有助于提高结果的准确性，反演得到如图10所示的结果，在图10中，左半图是初始模型，从上到下分别为纵波速度反射系数、横波速度反射系数以及密度反射系数.初始模型与地质先验信息以及井数据有关，是对工区的一个粗略的估计，所选择解的范围是在初始模型的基础上加减一个工区该参数的最大值，这样的一个范围被认为是比较合适的，因为所选取的范围至少要能包含合理的解，但是范围太大又会增加反演的多解性.另外一方面，如果得到了较好的初始模型，可以缩小解的约束范围，从而提高反演的效率和质量，但本文并非重点寻找更好的初始模型，而关心的是算法本身.图10的右半图是反演结果，从上而下分别是纵波速度反射系数、横波速度反射系数以及密度反射系数剖面，由初始模型和反演结果对比，初始模型可以确定解的范围以及初次迭代值，两者的相关性并不高，但是反演结果仍然比较理想.

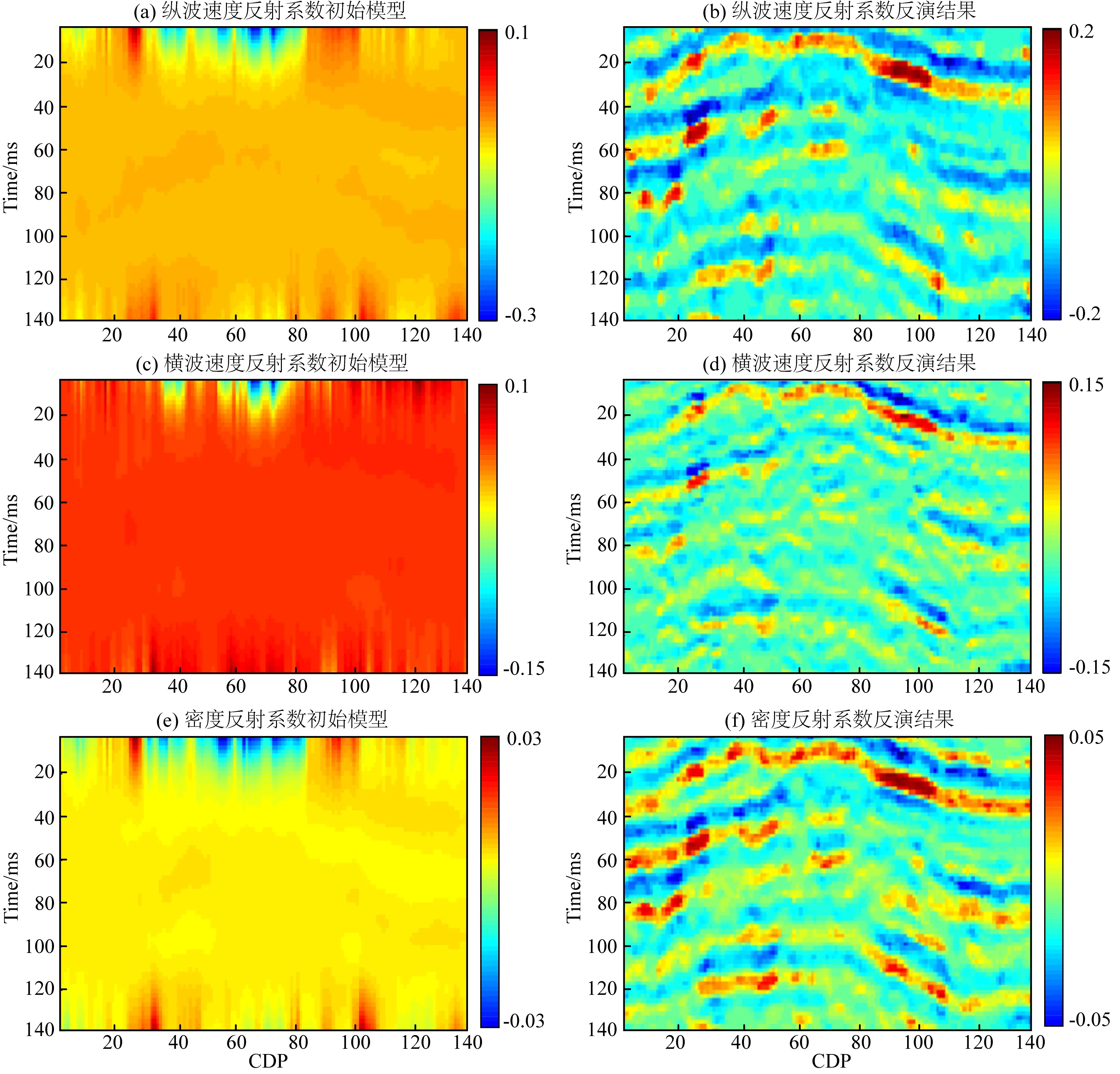
图10　纵波速度反射系数(上)横波速度反射系数(中)密度反射系数(下)剖面Fig.10　P-wave velocity reflection coefficient (top) wave velocity reflection coefficient (mid) density reflection coefficient (below) profiles

图11　反演值(第70道)(红色)与软件反演值(蓝色)对比Fig.11　Inversion value (70th trace) (red) and software inversion value (blue) contrast

反演结果整体效果体现出了地震有限频带内的信息，地震剖面上反射能量的强弱与反演结果是一致的，图10中红色代表高值，纵波速度整体上变化较大，而密度的变化较小，整体的横向连续性有待提高.为了验证结果的正确性，用某反演软件得到较为理想的反演剖面，随机抽出第70道与结果对比如图11所示，图中从左至右分别是纵波速度反射系数、横波速度反射系数以及密度反射系数，可以发现用逆算子估计算法反演得到的结果与用软件反演结果保持较好的一致性，两者在局部极值位置的反演结果有较好的统一.

5结论

本文采用Aki&Richards线性方程建立AVO反演方程，目标函数加入初始模型以及L1范数约束，采用非优化的逆算子估计算法进行求解，得到纵横波速度反射系数以及密度反射系数.模型试算证明算法可以增加对解的约束条件以及加入合理初始模型，加快收敛速度且提高解的可靠性，并且提高抗噪性.在处理实际资料时横向连续性和稳定性较差，可以通过优化目标函数以及优化初始模型的方法减小这个问题带来的影响.试验证明基于逆算子估计的AVO反演方法是有效并且具有较大潜力的.

References

Aki K, Richards P G. 1980. Quantitative Seismology: Theory and Methods. USA: W H Freeman & Co.

Bortfeld R. 1961. Approximations to the reflection and transmission coefficients of plane longitudinal and transverse WAVES.GeophysicalProspecting, 9(4): 485-502. Chen J J, Yin X Y. 2007. Three-parameter AVO waveform inversion based on Bayesian theorem.ChineseJournalofGeophysics(in Chinese), 50(4): 1251-1260.Downton J E, Lines L R. 2001. Constrained three parameter AVO inversion and uncertainty analysis.∥CSEG 2001 expanded abstracts. 251-254.

Downton J E, Lines L R. 2004. Three term AVO waveform inversion.∥SEG Technical Program Expanded Abstracts. 23(1): 215-218.

Goodway W, Chen T, Downton J. 1997. Improved AVO fluid detection and lithology discrimination using Lamé Petrophysical parameters “λρμρλμfluid stack” from P and S inversions.∥ SEG Annual Meeting Expanded Abstracts.

Gray D, Andersen E. 2001. The application of AVO and inversion to the estimation of rock properties.∥ SEG Annual Meeting Expanded Abstracts. 70: 549-552.

Kuzma H A, Rector J W. 2004. Non-linear AVO inversion using support vector machines.∥ 74th SEG Annual Meeting Expanded Abstracts. Ma X Q. 2001. Technical article: Global joint inversion for the estimation of acoustic and shear impedances from AVO derived P- and S-wave reflectivity data.FirstBreak, 19(10): 557-566.

Mogensen S, Link C. 2001. Artificial neural network solutions to AVO inversion problems.∥ 2001 SEG Annual Meeting Expanded Abstracts. Press F. 1968. Earth models obtained by Monte Carlo inversion.JournalofGeophysicalResearch, 73(16): 5223-5234.

Shuey R T. 1985. A simplification of the Zoeppritz equations.Geophysics, 50(4): 609-614. Simmons J L Jr, Backus M M. 1996. Waveform-based AVO inversion and AVO prediction-error.Geophysics, 61(6): 1575-1588. Tikhonov A N .1963. Solution of incorrectly formulated problems and the regularization method.SovietMathematicalDoklady, 4:1035-1038.

Yin X Y, Zhang S X. 2014. Bayesian inversion for effective pore-fluid bulk modulus based on fluid-matrix decoupled amplitude variation with offset approximation.Geophysics,79(5):R221-R232Yan P F, Zhang C S. 2005. Artificial Neural Networks and Evolutionary Computing (in Chinese). Beijing: Tsinghua University Press. Yang P J, Yin X Y. 2008. Non-linear quadratic programming bayesian prestack inversion.ChineseJournalofGeophysics(in Chinese), 51(6): 1876-1882.

Yin X Y, Wu G C, Zhang H Z. 1994 .The application of neural networks in the reservior prediction.JournaloftheUniversityofPetroleum(in Chinese), 18(5):20-26.

Yin X Y, Zhang S X, Zhang F C, Hao Q Y. 2010 .Elastic impedance inversion for reservoir description and fluid identification based on Russell approximation.OilGeophysicalProspecting(in Chinese),45(3): 373- 380.Yin X Y, Zong Z Y, Wu G C. 2013. Improving seismic interpretation: a high-contrast approximation to the reflection coefficient of a plane longitudinal wave.PetroleumScience, 10(4): 466-476. Yin X Y, Cao D P, Wang B L, Zong Z Y. 2014 . Progress on fluid identification method based on pre-stack seismic inversion.OilGeophysicalProspecting(in Chinese), 49(1)：22-34,46.

Yin X Y, Cui W, Zong Z Y, et al. 2014. Petrophysical property inversion of reservoirs based on elastic impedance.ChineseJ.Geophys.(in Chinese), 57(12): 4132-4140.

Yin X Y, Zong Z Y, Wu G C. 2015. Research on seismic fluid identification driven by rock physics.ScienceChinaEarthSciences, 58(2): 159-171. Zheng X D. 1991. The approximate equations of Zoeppritz equation and its applications.OilGeophysicalProspecting(in Chinese), 26(2): 129-144.

Zong Z Y, Yin X Y, Zhang F, et al. 2012. Reflection coefficient equation and pre-stack seismic inversion with Young′s modulus and Poisson ratio.ChineseJ.Geophys. (in Chinese), 55(11): 3786-3794, doi: 10.6038/j.issn.001-5733.2012.11.025. Zong Z Y, Yin X Y, Wu G C. 2012. AVO inversion and poroelasticity with P- and S-wave moduli.Geophysics, 77(6): N17-N24.

Zong Z Y, Yin X Y, Wu G C. 2013a. Elastic impedance parameterization and inversion with Young′s modulus and Poisson′s ratio.Geophysics, 78(6): N35-N42. Zong Z Y, Yin X Y, Wu G C. 2013b. Multi-parameter nonlinear inversion with exact reflection coefficient equation.JournalofAppliedGeophysics, 98: 21-32.

Zong Z Y, Yin X Y, Wu G C, et al. 2015. Elastic inverse scattering for fluid variation with time-lapse seismic data.Geophysics, 80(2): WA61-WA67.

附中文参考文献

陈建江, 印兴耀. 2007. 基于贝叶斯理论的AVO三参数波形反演. 地球物理学报, 50(4): 1251-1260.

阎平凡, 张长水. 2005. 人工神经网络与模拟进化计算. 北京: 清华大学出版.

杨培杰, 印兴耀. 2008. 非线性二次规划贝叶斯叠前反演. 地球物理学报, 51(6): 1876-1882.

印兴耀, 吴国忱, 张洪宙. 1994 .神经网络在储层横向预测中的应用.石油大学学报:自然科学版, 18( 5): 20 -26.

印兴耀, 张世鑫, 张繁昌, 郝前勇. 2010 .利用基于Russell 近似的弹性波阻抗反演进行储层描述和流体识别. 石油地球物理勘探, 45(3): 373-380.

印兴耀，曹丹平，王保丽，宗兆云. 2014 .基于叠前地震反演的流体识别方法研究进展.石油地球物理勘探，49(1): 22-34,46.

印兴耀, 崔维, 宗兆云, 刘晓晶. 2014.基于弹性阻抗的储层物性参数预测方法研究. 地球物理学报, 57(12): 4132-4140.

郑晓东. 1991. Zoeppritz方程的近似及其应用. 石油地球物理勘探, 26(2): 129-144.

宗兆云, 印兴耀, 张峰等. 2012. 杨氏模量和泊松比反射系数近似方程及叠前地震反演. 地球物理学报, 55(11): 3786-3794.

(本文编辑胡素芳)

AVO inversion based on inverse operator estimation

YIN Xing-Yao, DENG Wei, ZONG Zhao-Yun

Geo-ScienceandTechnologyFaculty,ChinaUniversityofPetroleum,QingdaoShandong266580,China

AbstractAmplitude variation with amplitude or angle (AVO/AVA) inversion has been widely utilized in exploration geophysics to estimate the formation of elastic parameters underground. The traditional inversion algorithms are mainly optimization, while the AVO inversion based on inverse operator estimation is to inverse directly. The key is to find the subspaces which exist inverse mapping instead of searching for the solution directly as optimization algorithms do.

基金项目国家重点基础研究发展计划(2013CB228604)，国家油气重大专项(2011ZX05030-004-002)，中国博士后科学基金(2014M550379),山东省博士后基金(201401018)和山东省优秀中青年科学科研奖励基金(2014BSE28009)联合资助.

作者简介印兴耀，男，中国石油大学(华东)教授.主要从事地球物理理论与方法方面的研究. E-mail： xyyin@upc.edu.cn

doi:10.6038/cjg20160426 中图分类号P631

收稿日期2015-03-20，2015-10-08收修定稿

印兴耀, 邓炜, 宗兆云. 2016. 基于逆算子估计的AVO反演方法研究.地球物理学报，59(4):1457-1468,doi:10.6038/cjg20160426.

Yin X Y, Deng W, Zong Z Y. 2016. AVO inversion based on inverse operator estimation.ChineseJ.Geophys. (in Chinese),59(4):1457-1468,doi:10.6038/cjg20160426.