金属橡胶内螺旋金属丝微动磨损预测模型研究*

2023-02-06肖笃平任志英黄健萌黎洪银路纯红王秦伟

润滑与密封 2023年1期

肖笃平任志英黄健萌黎洪银路纯红王秦伟

(1.福州大学机械工程及自动化学院福建福州 350116；2.福州大学金属橡胶与振动噪声研究所福建福州 350116；3.河北工业职业技术学院汽车工程系河北石家庄 050091)

金属橡胶作为一种非连续性多孔的弹性金属元件，与传统橡胶材料相比具有能够适应多种恶劣工作环境、不易老化失效等优点，且具有优异的缓冲吸震、隔振阻尼等性能，因此被应用在航空航天、军事装备等多个高科技领域中。而特殊的制备工艺流程使得金属橡胶内部细金属丝(丝径0.05～0.3 mm)之间相互啮合、交错勾连，在受到外界载荷时，金属丝之间将发生挤压、滑移摩擦等现象。因此，长时间的微动滑移将使得细金属丝表面发生磨损以及损伤，最终导致金属丝发生疲劳断裂(见图1)，进而演变为整个金属橡胶构件的性能退化与失效，影响其使用寿命，增加工业成本[1-2]。因此，金属橡胶内部金属丝之间随机接触形态下的微动磨损模型研究,对探究金属橡胶构件的磨损失效与使用寿命预测具有重要意义。

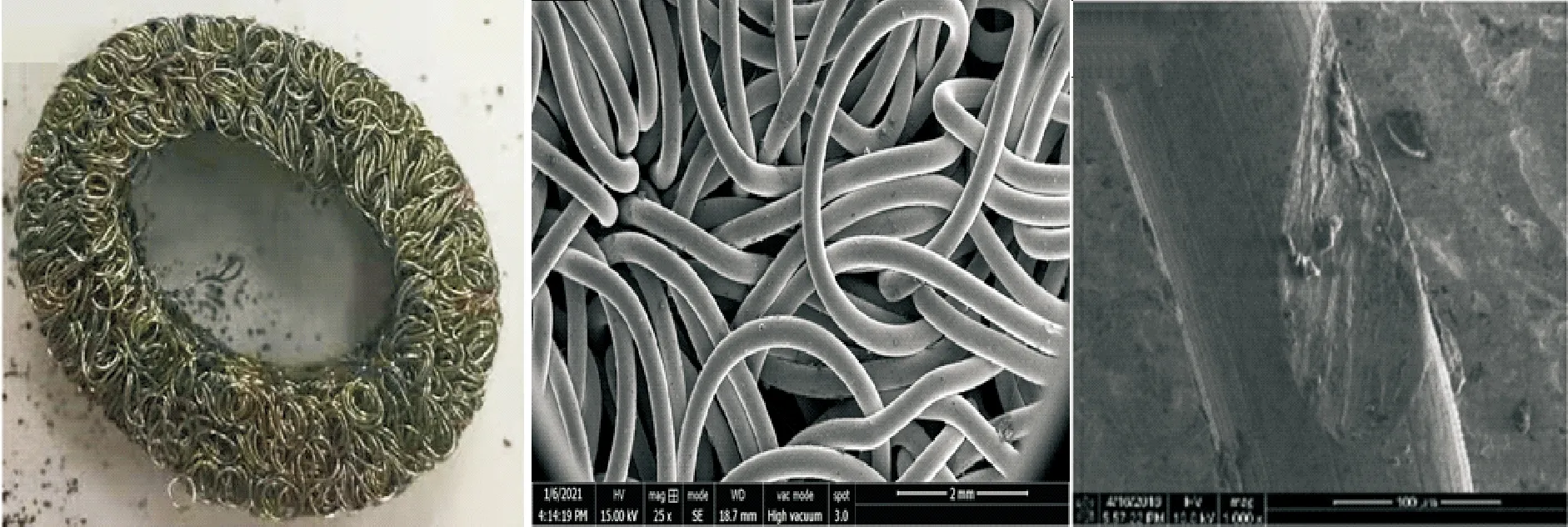
图1 金属橡胶宏/微观磨损示意

现有关于金属橡胶内金属丝微动摩擦磨损的研究，主要探究了不同微动因素对磨损结果的影响规律。如董秀萍等[3-4]探究了金属丝在不同载荷下的微动摩擦磨损性能,对金属橡胶隔振构件进行疲劳试验，并对金属丝疲劳断裂的原因进行了分析。侯军芳等[5]运用电镜和X射线技术，对金属丝进行金相观察分析，分析了不锈钢丝动态加载疲劳断口的形貌特征。黄明吉等[6]研究了金属橡胶不锈钢丝丝径对摩擦磨损行为影响的规律及机制，建立了磨损深度与丝径之间的定量关系。除此之外，沈燕、CRUZADO、范娜等人[7-9]探究了不锈钢钢丝在不同接触载荷下的微动摩擦磨损性能；张德坤、王大刚等[10-11]考察了接触载荷、循环次数和微动振幅3个因素对钢丝试样磨损深度和摩擦性能的影响；CRUZADO等[12]探究了金属丝在不同夹角下的微动磨损特性。然而，关于金属丝微动磨损预测模型的研究较少，目前应用较为广泛的是Archard磨损模型，且多结合有限元分析，但其主要探究磨损过程的有限元实现与优化，并没有建立有效的预测模型[13-15]。OUT和VON MORGEN[16]应用几何学仅对几种常见形状的磨损体积进行了建模计算，并没有对其他磨损表征参数进行拓展分析。ARGATOV等[17]考虑磨损系数对接触压力的依赖作用，对典型的垂直接触状态下磨损深度模型进行了参数优化，但对于锐角接触状态的模型并没有深入探究。CRUZADO等[13]提出椭圆积分计算椭圆磨痕长短轴的计算模型，但其中涉及综合刚度、综合弹性模量等不易确定的参数且模型复杂，计算较为困难，不适用于金属橡胶存在多接触点且复杂的结构。

综上所述，目前关于金属丝微动磨损预测模型的研究仅垂直接触状态下较为成熟，而对于锐角接触预测模型的研究，存在模型不成熟、计算复杂以及未将磨损深度与磨痕长度相关联等问题，不适用于金属橡胶内部金属丝的微动磨损预测。

基于此，本文作者对金属橡胶内部金属丝微动磨损的有限元仿真结果进行了分析，根据螺旋金属丝与直金属丝磨损结果相差较小，将微动滑移状态下的螺旋接触对理想化为直金属丝接触对，以磨损深度、磨痕尺寸为磨损表征参数，探讨不同接触形态下金属丝微动磨损特征的演化规律，分析磨痕夹角与金属丝接触夹角的关系；以垂直接触磨损模型为基础，建立任意接触角度下的磨损形貌特征预测模型，为预测金属橡胶内部金属丝微动磨损和使用寿命提供了理论基础。

1 几何建模及有限元分析

1.1 有限元几何建模及参数设置

为了准确地反映金属橡胶内部金属丝复杂无序的接触形态，基于现有的金属橡胶模型虚拟制备技术[18]，得到成型后内部金属丝之间的接触形态，如图2所示。

图2 金属橡胶数值模型金属丝接触示意

由图2所示数值几何模型可知，金属橡胶内部金属丝呈现为螺旋弯曲的形态，并与其他金属丝交缠勾连与啮合相嵌，当受到外载荷作用时，内部接触点将会发生微米级别的摩擦磨损现象[19]。为了确定金属丝的螺旋曲率对于其微动磨损的影响，取任意相同微动试验参数，应用MSC.Marc软件对螺旋金属丝(选用曲率影响最大时的微元弹簧接触对模型)与直金属丝进行微动磨损有限元分析，观察两者的磨损结果，具体参数设置与结果如表1所示。可知，在同等试验条件下，螺旋金属丝接触对磨损深度较直金属丝略小，但两者相差仅为5.8%，故可将金属橡胶内部金属丝之间的微动磨损理想化为直金属丝的微动磨损，即螺旋金属丝的曲率对微动磨损的影响较小，可不作考虑。

文中以直金属丝接触微元为研究对象进行有限元建模，对金属丝接触点处局部网格进行多种尺寸大小的精细化分，结果误差小于5%，与文献[15]中结论一致。故考虑丝径大小将精细网格尺寸设置为4 μm×4 μm，材料采用常见的304不锈钢，金属丝之间的摩擦因数按经验值取为0.15，磨损系数采用磨损后期稳定阶段的平均值。对上金属丝施加接触载荷，下金属丝进行循环微动，采用磨损深度、磨损体积以及磨痕尺寸等参数表征金属丝的微动摩擦磨损行为。而内部金属丝的无序性主要体现为金属丝之间接触夹角的随机性，故文中重点探究接触夹角对于金属丝微动磨损结果的影响程度与变化规律。

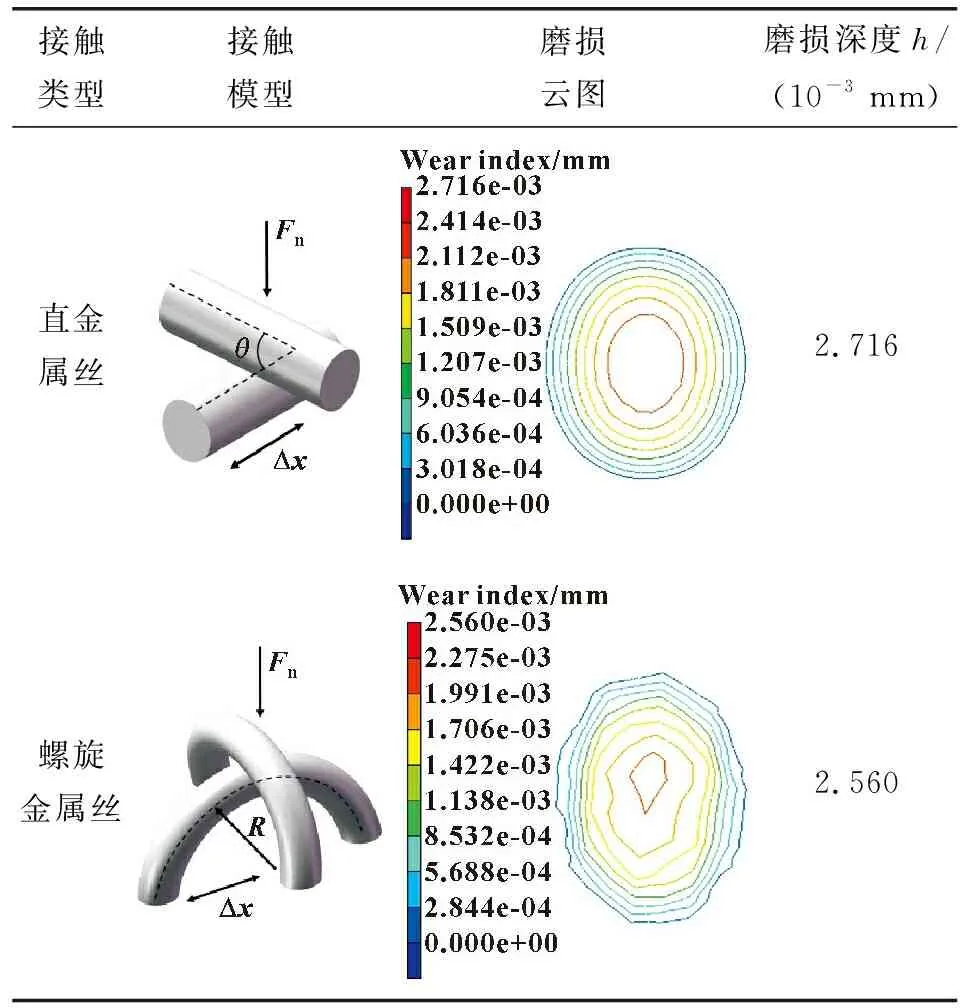
表1 2种接触类型微动磨损结果

试验参数设置参照文献[20]中金属橡胶数值模型被压缩0.6 mm时得到的间接参考参数，具体可如表2所示。

表2 微动磨损仿真实验参数

1.2 有限元结果分析

金属丝接触微元可看作理想圆柱体，受到载荷作用之前金属丝之间为点接触状态；当施加作用力Fn后，根据赫兹接触理论，接触点开始发生弹性变形，接触点处的应力分布如图3所示。可以发现无论是垂直交叉接触还是任意接触夹角接触，其接触中心点处的接触应力最大，故金属丝磨损后，接触中心点处磨损现象最严重。

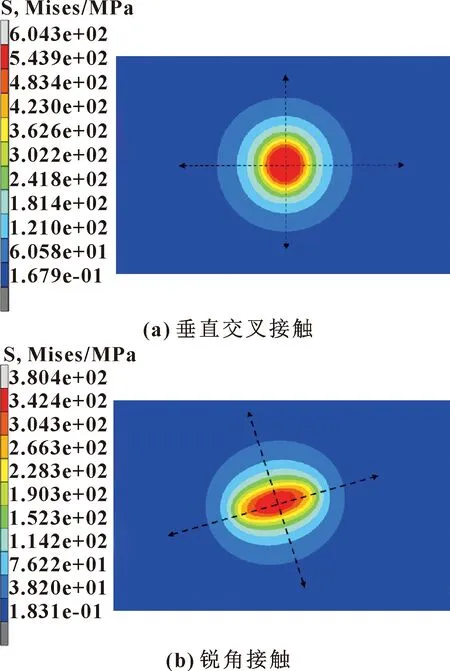
图3 金属丝初始接触应力云图

1.2.1 接触夹角对磨损特性的影响规律

金属丝以不同夹角接触摩擦时，仿真得到的磨损深度与磨损体积随时间的动态变化规律如图4所示。可知，随着接触夹角的不断增大，任意时刻产生的磨损深度与磨损体积均增大；以不同夹角接触时，其磨损深度与磨损体积均随微动时间的增加而不断增大，其中磨损深度呈现出非线性增大趋势，磨损后期增大趋势逐渐平缓。

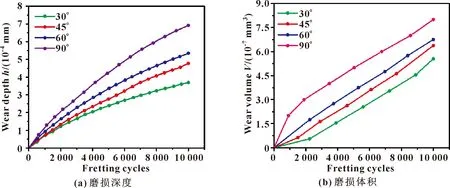
图4 不同夹角接触时金属丝磨损结果随微动周次的变化

仿真得到的不同接触夹角下磨损形貌等值线图以及磨痕尺寸变化曲线如图5所示。从图5(a)—(d)中可知，锐角交叉下的磨损形貌呈现为椭圆状，而垂直交叉下的磨损形貌近似为圆形。由图5(e)可知，随着接触夹角的不断增大，椭圆磨痕的长半轴长度在不断减小而短半轴长度在不断增大，最后在垂直交叉下长短半轴长度近乎一致，即呈现为圆形状磨痕。由图5(f)可知，金属丝的最大磨损深度与磨损体积都随着接触夹角的增大而逐渐增大，这主要是由于在磨损过程中随着金属丝接触夹角的不断增大，金属丝之间的实际接触面积反而在不断减小，使得接触界面的接触正应力不断增大，所以磨损程度加深。

图5 不同接触夹角下磨损形貌等值线和磨痕尺寸变化

1.2.2 不同接触夹角下金属丝磨痕的特性研究

为了更好地找出金属丝之间接触形态与磨损形貌之间的关系，对不同接触夹角与所形成磨痕夹角之间的关系进行统计分析，见图6。通过磨痕云图结果分析可知，当线匝垂直交叉时，磨痕与金属丝之间呈对称分布；当线匝之间为任意锐角交叉时，椭圆状磨痕长轴与金属丝轴线之间的夹角不再是接触夹角。通过对仿真结果的磨痕长轴与金属丝轴线之间的夹角进行测量分析，得到不同接触状态下磨痕夹角与接触夹角的关系如图7和表3所示。

图6 线匝接触夹角与磨痕夹角示意

图7 磨痕夹角与线匝接触夹角关系

表3 不同锐角接触下的磨痕夹角

根据上述对磨痕夹角的测量分析可知，在任意锐角交叉下，磨痕夹角大小近似为金属丝接触夹角的1/2(考虑仿真以及测量的误差)；对于垂直交叉，亦可认为磨痕与金属丝的夹角为45°。同时，锐角交叉下金属丝磨损界面承受压力的区域亦为椭圆状，并且该椭圆区域的长轴与线匝之间的夹角刚好为金属丝接触夹角的1/2[13,21]，进一步佐证了这一观点。其特有的磨痕特点主要是由于金属丝特别的圆弧表面几何特征，具体如图8所示。

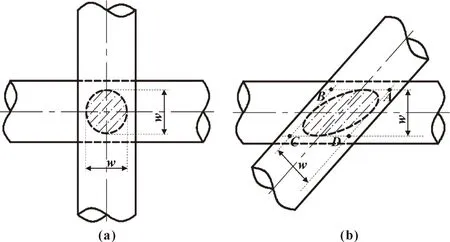
图8 垂直接触(a)和任意锐角接触(b)下金属丝磨损磨痕示意

如图8所示，假设任一深度时磨痕的最大宽度为w，当金属丝垂直相交时，磨痕的任一方向上的最大宽度近似都为w，而当金属丝以任一锐角相交并具有相同磨损深度时，上下线匝表面的最大宽度不受影响即同样为w[22]。如图8(b)所示，假设金属丝的接触夹角为θ，最大宽度界线形成平行四边形ABCD，由几何关系可知，四边形的两组高度即为磨痕的最大宽度值w，所以四边形ABCD的四条边都相等。由此可知四边形ABCD为一个菱形并且椭圆磨痕与菱形的四条边都相切，所以椭圆的长轴为金属丝夹角的角平分线，即椭圆磨痕夹角为金属丝接触夹角的1/2。并且根据金属丝接触状态可知，最大宽度边界线经过金属丝中线接触点处，即切点为各边中点，故可得接触夹角与磨痕夹角的关系：

(1)

式中：α为磨损磨痕夹角；θ为金属丝接触夹角。

2 任意接触形态下磨损数值模型

在上述研究中，主要分析了接触夹角对金属丝微动磨损的影响规律，同时通过对仿真数据的统计计算以及几何分析，发现任意接触夹角与磨痕夹角的特殊大小关系。据此，文中以垂直交叉下的磨损演化数值模型为基础，通过金属丝磨痕的特殊几何关系建立任意锐角接触下的磨损演化模型。

2.1 Archard磨损理论

Archard模型主要假设物体的磨损量与物体之间的接触力学的计算结果相关，经过多年的研究发展，其中的力学影响形式可以分为多种形式，主要有正压力、表面摩擦力、剪切力等形式[23]。文中研究认为金属丝之间的磨损主要由正压力所导致的，一般可写成下式[18]所示：

(2)

式中：h为磨损深度；k为磨损系数；p为接触压力；ds为滑动距离。

因此，磨损深度计算公式可表示为

(3)

2.2 微动磨损演化模型

(4)

(5)

(6)

式中：a0为接触初始半径；a为磨痕半宽；υ为泊松比；E为弹性模量；R为金属丝半径；F为接触正压力；Δx为微动行程；N为微动周次；h为磨损深度。

根据上文分析，磨痕夹角与金属丝接触夹角之间存在1/2的特殊几何关系，因此以金属丝的接触中心为原点建立坐标系，探究任意接触角度下椭圆形磨痕长、短半轴的演化规律，如图9所示。

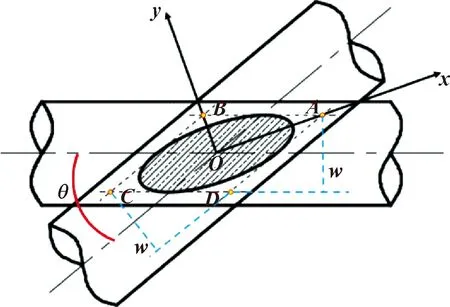
图9 任意锐角交叉下磨损磨痕坐标示意

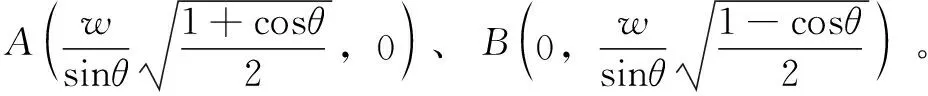
(7)

因此，椭圆轮廓的导数方程为

(8)

将式(8)以及切点坐标代入椭圆轮廓基本方程中，即可得椭圆磨痕轮廓的长、短半轴与接触宽度的关系为

(9)

(10)

式中：m、n分别为磨痕长短半轴；w为接触宽度；θ为接触夹角。

故可得椭圆磨痕长、短半轴长度的关系为

做好高校学生管理工作，不仅有利于促进学生的全面发展，还有利于培养学生的综合素养。但近年来，随着高校学生的连年增多，高校学生管理工作出现了各种各样的问题，为了有效提升高校学生管理工作的质量与成效，必须从根本上解决这些问题。因此，详细研究当前高校学生管理工作的瓶颈与突破是很有必要的，本文提出了高校学生管理工作的新思路与新方法，它在一定程度上能够推进高校管理工作的改革，从而建设适宜师生工作与学习的和谐校园。

(11)

在微动磨损的后期稳定阶段，除了接触界面的边缘部分存在应力集中现象，接触面的接触压力几乎为均匀分布，因此稳定阶段椭圆磨痕界面的接触压力可以表示为

(12)

将式(11)、(12)代入式(3)中，即可得任意接触角度下的磨损深度演化模型：

(13)

式中：θ为线匝接触夹角；n为椭圆磨痕短半轴长度；n0为椭圆磨痕短半轴初始长度。

由于椭圆磨痕短半轴长度演化规律与垂直交叉时的接触半宽相似[22]，考虑接触夹角的影响以及误差，可将椭圆磨痕的磨损深度演化模型式(13)假设改写为如下形式：

(14)

式中：K(θ)为考虑接触夹角的校正参数。

根据文献[21]，锐角夹角下的磨损体积为垂直接触下的磨损体积的1/sinθ。因此可假设磨痕短轴与垂直接触圆形磨痕半宽的演化关系也与接触夹角有关，并且通过与有限元结果拟合对比分析，可设定校正参数K(θ)为(1+sinθ)/sinθ，即任意锐角接触状态下磨损深度的演化模型如下式所示：

(15)

将式(4)、(5)代入式(15)中，即可得包含材料属性、几何特性以及环境因素等参数的微动磨损演化预测模型，如式(16)所示。

(16)

式(16)将任意锐角接触下磨损深度与各微动参数联系起来，根据式(16)得到稳定阶段平均参数下的磨损深度与各微动参数之间的演化关系，如图10所示。

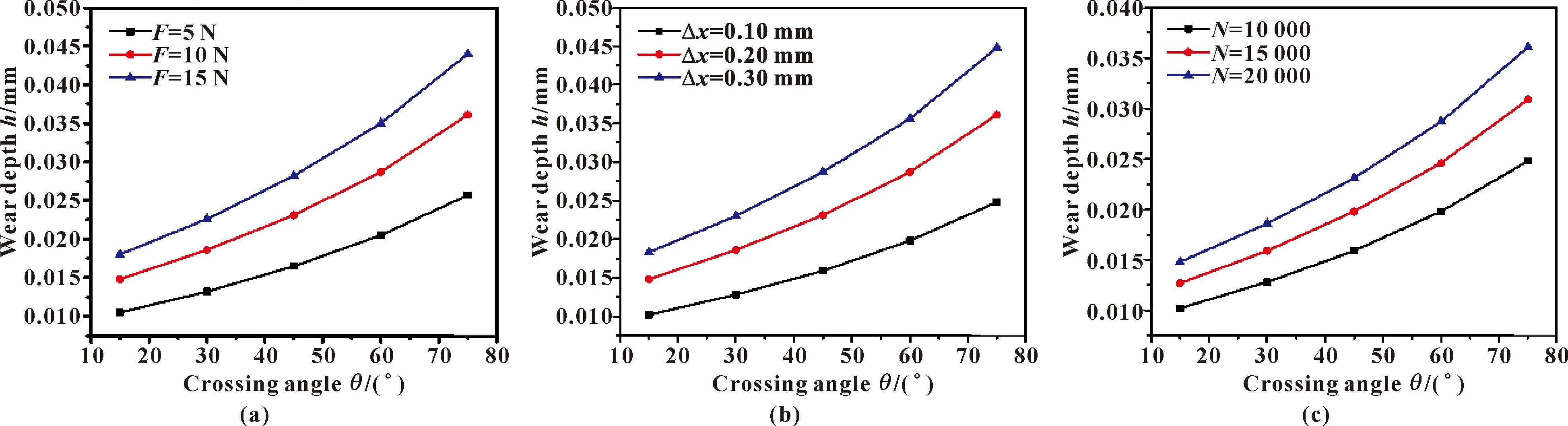
图10 不同夹角下磨损深度与接触载荷(a)、微动行程(b)与微动周次(c)变化关系

根据弦长与弧长的几何关系，垂直交叉金属丝磨损深度与磨损宽度的关系可由式(17)得到。而对于金属丝圆柱表面，磨损深度一定情况下在表面形成的磨损宽度是一定的，故任意接触角度下同样适用。

(17)

式中：R为曲率半径；w为接触宽度；h为对应弧高。

将式(17)分别代入式(9)、(10)中，椭圆磨痕的长、短半轴长度演化模型可表示为

(18)

(19)

式中：f为误差系数。式(18)、(19)将任意接触夹角下椭圆磨痕的尺寸参数与各微动参数联系起来，根据式(18)、(19)得到磨痕长短半轴长度与各微动参数之间的变化关系，具体如图11所示。

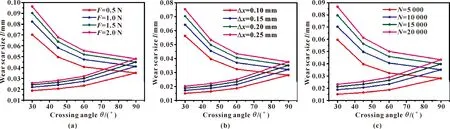
图11 不同夹角下磨痕尺寸与接触载荷(a)、微动行程(b)、微动周次(c)变化关系

3 模型验证

由于条件所限，为了验证上述预测演化模型的适用性与正确性，文中将基于已有相关文献中的细金属丝微动磨损实验数据进行验证分析。文献中的试验均采用往复式微动磨损试验机，试验材料主要为钢丝绳细丝，主要以磨损深度、椭圆磨痕尺寸为表征参数，采用扫描电镜与测量仪对金属丝磨损表面进行测试观察，以探究不同接触载荷、微动行程、接触夹角以及不同周次对金属丝磨损的影响。

3.1 磨损深度演化模型验证

基于王大刚[11]、CRUZADO等[12-13]的细金属丝微动磨损试验，对磨损深度模型进行验证分析，主要试验参数设置如表4所示。将试验参数代入上述预测模型中，考察金属丝微动磨损过程中不同微动参数下磨损深度试验值与理论值之间的吻合度(其中磨损系数详细见参考文献)。

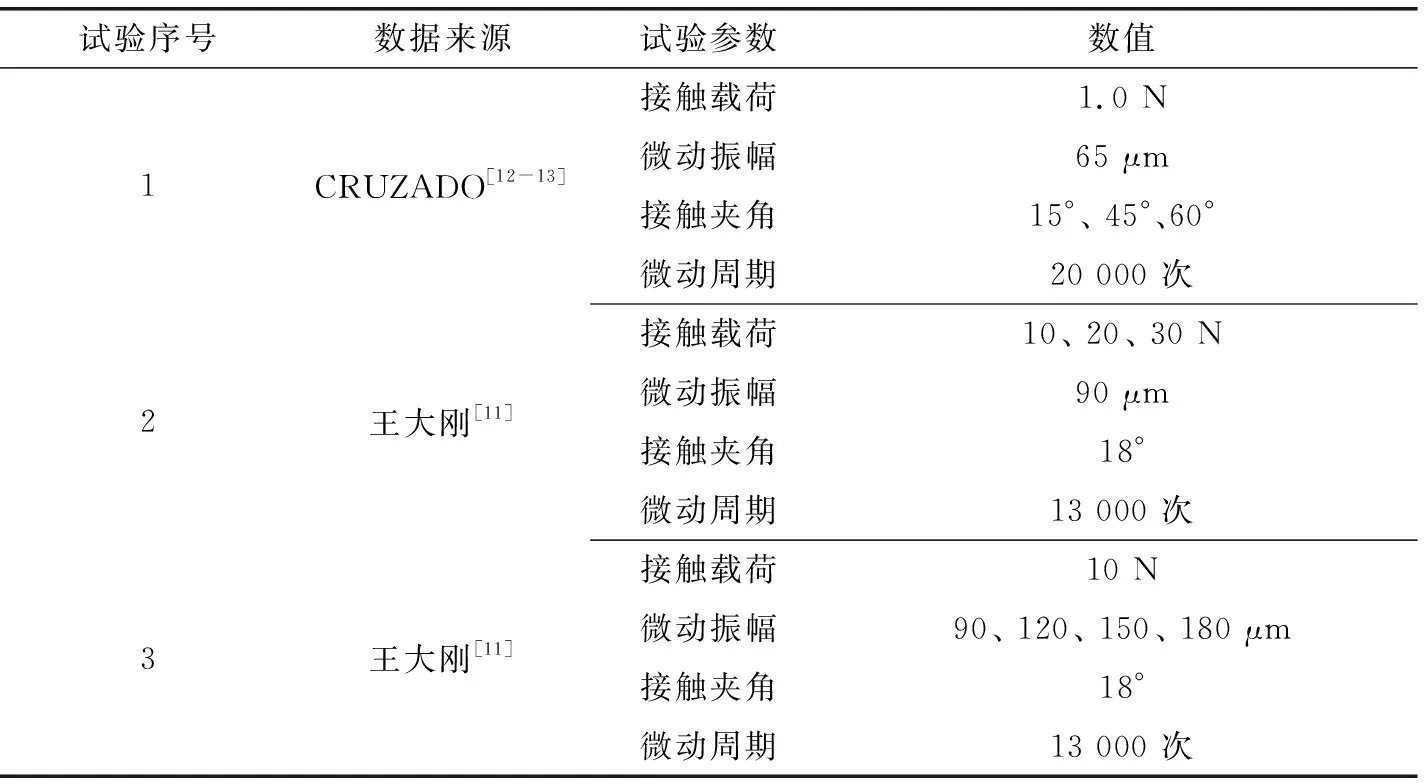
表4 金属丝微动磨损试验参数[11-13]

使用电子显微镜观察金属丝在接触夹角分别为15°、30°、45°、60°、75°下的微动磨损缺口，如图12所示。磨痕则近似呈现为椭圆状，利用磨痕测微仪对金属丝磨损深度进行测量，得到不同参数下金属丝的磨损深度试验值。将试验值与理论值进行对比，得到文中预测模型的精确度如图13所示。

图12 不同夹角下钢丝磨损缺口的扫描电子显微镜照片[12-13]

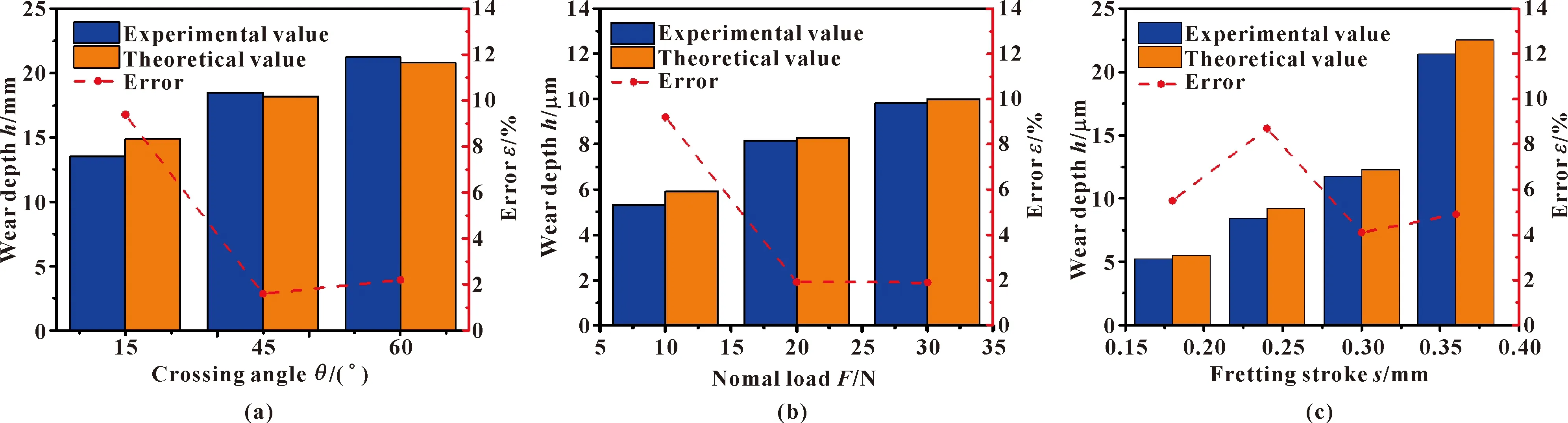
图13 不同接触夹角(a)、接触载荷(b)、微动行程(c)下磨损深度试验值与预测值对比

由图13可知，不同微动参数下磨损深度的预测值与试验值吻合较好，预测值较试验值普遍偏大，两者之间的误差保持在10%以内，故文中提出的磨损深度预测模型具有良好的预测效果，为进一步预测金属橡胶磨损提供了一种途径。

3.2 磨痕尺寸演化模型验证

当金属丝以锐角交叉磨损形成椭圆状的磨痕，磨痕的长短轴长度是一个至关重要的磨损参数。基于CRUZADO等[13]的细金属丝微动磨损试验，对磨痕尺寸模型进行验证分析，主要试验设置参数如表5所示。利用显微测量仪对椭圆磨痕的长短轴长度进行测量，得到不同接触角度下钢丝磨痕长短轴的试验值，再将试验值与文中计算的理论值进行对比，结果如图14所示。可知，不同接触夹角下磨损深度的预测值与试验值吻合较好，除在15°接触角时长轴长度预测误差较大，其余接触情况下两者之间的误差可保持在10%以内。考虑到夹角较小时磨损测量会出现误差，摩擦试验的试验结果可能呈现大于15%的分散性[24]，故是可以接受的。因此，文中提出的微动磨损模型能够较好地预测任意接触锐角磨损磨痕的形状尺寸，对于进一步了解金属丝的磨损行为提供了一种有效途径。