结构参数对贯通挡板袋型阻尼密封动力特性的影响*

2023-02-06曹世裕李剑钊荆建平

润滑与密封 2023年1期

张旭曹世裕孙丹李剑钊荆建平

(1.上海交通大学机械系统与振动国家重点实验室上海 200240；2.哈尔滨船舶锅炉涡轮机研究所(中国船舶重工集团公司第七〇三研究所) 黑龙江哈尔滨 150001)

在涡轮机转子-密封-轴承系统中，轴承一般安装在转子的两端，该处振幅极小，不能有效地抑制长转子的振动；而密封因安装灵活、数量多，可成为抑制转子振动的潜在手段之一。自ALFORD[1]在对航空发动机转子失稳研究中首次关注密封的动力学效应以来，许多学者开始研究如何避免因密封造成的转子失稳，以及如何通过合理的密封设计为转子系统提供额外的阻尼。VON PRAGENAU[2]第一次提出阻尼密封的概念，指出凹凸不平的静子表面能够有效提高密封-转子系统的阻尼，由此产生了蜂窝密封等结构形式。VANCE等[3-5]指出由于有周向流动带来的显著的交叉阻尼作用，ALFORD[1]提出的bulk-flow模型不能准确描述迷宫密封，并提出了一个用挡板分隔迷宫密封腔室，阻止气流周向流动的新结构，即袋型阻尼密封。袋型阻尼密封由于结构简单，获得了广泛的应用。如图1所示[6]，典型的袋型阻尼密封由交替排列的基本腔室和二次腔室组成，基本腔室被周向的挡板分隔。为了获得正阻尼，基本腔室设计成发散型间隙，与之配合，二次腔室设计成收敛型间隙。

文中所述贯穿挡板袋型阻尼密封，其二次腔室也被挡板贯穿，进一步削弱周向环流对其动力特性的影响，其结构如图 2所示[7]。针对该型密封结构参数对动力特性的影响，国内外学者做了大量工作。GRIEBEL[8]研究了袋型阻尼密封有效腔室齿顶间隙凹槽位置和排列方式对动力学特性的影响，结果表明一个腔室搭配一个凹槽的结构设计使得动力学特性系数达到最优。张万福等[9]提出了一种基于变厚度挡板的新型渐扩/渐缩袋型阻尼密封，并研究了其密封动力特性。MOORE[10]使用SCISEAL计算了8齿迷宫密封动力学特性。HIRANO等[11]使用CFX-TASC-Flow软件仿真计算了汽轮机转子迷宫密封的刚度和阻尼系数。刘晓锋和陆颂元[12]采用FLUENT分析计算了5齿空压机转子迷宫密封的动力学特性。CHOCHUA 和SOULAS[13]根据动网格技术和非定常CFD方法提出了“单频单向涡动模型”。 PUGACHEV等[14]给转子施加椭圆涡动轨迹以便求解袋型阻尼密封动力特性，发现求解效果良好。孙丹等人[15]研究了袋型阻尼密封动特性对转子稳定性的影响。司和勇等[16]分析了密封结构对汽轮机转子动力特性的影响。

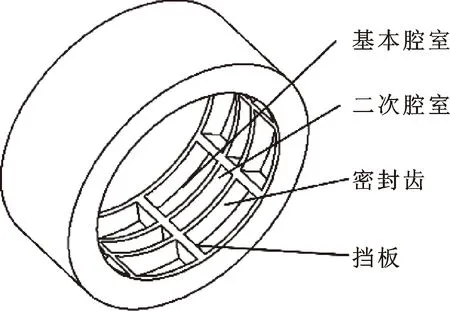
图2 贯穿挡板袋型阻尼密封结构[7]

作为该领域工作的补充，本文作者针对贯通挡板袋型阻尼密封的动力特性，基于扰动法与CFD方法，探究腔室深度、密封间隙、基本腔室宽度3种结构参数对其动力特性的影响规律，为贯通挡板袋型阻尼密封的结构尺寸设计提供参考。

1 密封-转子系统动特性系数求解方法

文中采用扰动法求解密封-转子系统的动特性系数。当转子在平衡位置附近发生涡动时，密封间隙随之发生周期性变化，又由于轴颈旋转运动和密封两侧的压差作用，间隙内流体在轴颈表面发生周期性的压力变化，由此产生刚度和阻尼作用。

求解时，通过CFD方法获得轴颈按给定参数涡动时轴颈表面的压力分布，列出轴颈受力方程，解出8个动特性系数。

下面就轴颈受力分析和轴颈表面流体力求解做详细说明。

1.1 扰动下轴颈的受力分析

密封-转子系统可以简化为如图3所示用8个动特性系数描述的动力学模型。

若转子在密封轴心附近产生一个小扰动Δx、Δy，密封对转子的作用力ΔFx、ΔFy为

(1)

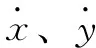
图3 转子-密封系统的力学模型

此时不论x、y还是Fx、Fy均包含了幅值和相位2个信息，将动态位移Δx、Δy与受力ΔFx、ΔFy做傅立叶级数(FS)并取一次谐波分量，可得：

(2)

(3)

将式(2)、(3)代入式(1)，可得：

(4)

此时若通过仿真计算等手段求出转子在给定频率Ω下的涡动轨迹x、y及相应的轴颈径向力Fx、Fy，即可通过式(4)求解轴承动特性系数。

通常，在考虑交叉刚度Kxy、Kyx与交叉阻尼Cxy、Cyx时，式(4)中未知数个数多于方程个数。一般通过增加扰动工况来补充方程，即增加激励组合的数目。如图4所示，若轴颈依虚线所示椭圆轨迹涡动(为方便叙述，用轨迹长轴方向指称激励方向)，x、y方向激励各可以贡献一组方程。此时方程与未知数数目一致，解此线性方程组可得8个动特性系数。

图4 y方向(a)、x方向激励(b)的椭圆涡动轨迹

1.2 沿椭圆轨迹涡动时轴颈力的仿真计算

在给定涡动下的轴颈所受径向力需要通过对流体域压力分布求解得到。文中用FLUENT计算当轴颈做图4所示单频椭圆涡动时轴颈表面压力分布。

贯通挡板袋型阻尼密封与转子之间的密封流体区域由密封间隙区域、基本腔室区域和二次腔室区域组成，以周向挡板数为8、密封齿数为6的袋型阻尼密封为例，通过ANSYS ICEM CFD建立贯通挡板袋型阻尼密封流体区域的结构化网格如图 5所示。

图5 贯通挡板袋型阻尼密封流域的结构化网格

为了控制施加到转子表面的单频椭圆涡动位移，文中采用了FLUENT19.0中的动网格技术，通过加载UDF，在三维非定常CFD数值计算求解器中输入单频椭圆涡动位移。

三维非定常CFD数值计算流程如图6所示，在前述网格的基础上，先对其进行稳态求解，获得初始边界条件。在此基础之上再对其进行三维非定常的CFD数值计算，即瞬态求解。并在转子表面设置监控点，通过积分的方式从中提取出转子涡动位移信号和流体激振力信号。

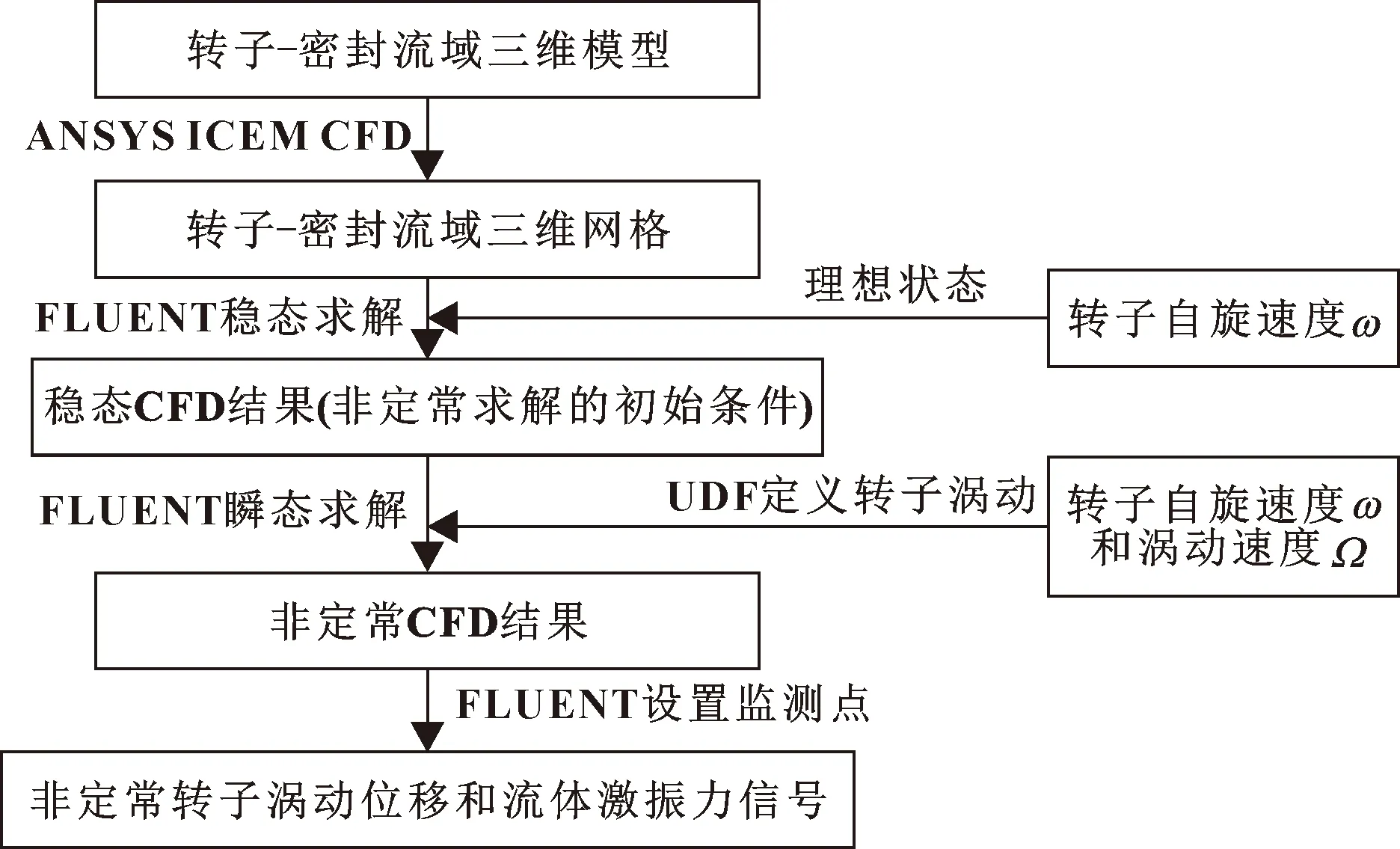
图6 三维非定常CFD数值计算的流程

进一步地，FLUENT求解器通过Monitors监控轴颈表面上每个网格单元的压力，对整个轴颈表面进行积分，最终得到每一时刻轴颈在x、y方向上受到的径向力:

(5)

式中：k为上文所规定的加载方向；Fkx、Fky表示轴颈所受的时域径向力；S表示密封所对应轴颈表面区域；pk为轴颈压力分布；φ为轴颈表面点角坐标。

求Fkx与Fky的傅立叶级数，取轴颈涡动频率对应的分量，可得Fkx和Fky。代入式(4)中，即可求得该密封-转子系统的动特性系数。

2 计算结果与讨论

在上述方法基础上，探究了腔室深度、密封间隙和腔室宽度这3个结构参数对贯通挡板袋型阻尼密封动力学特性的影响规律。

2.1 结构参数和仿真输入

以某汽轮机用贯通挡板袋型阻尼密封为例进行讨论，所述密封部分结构参数如表1所示。

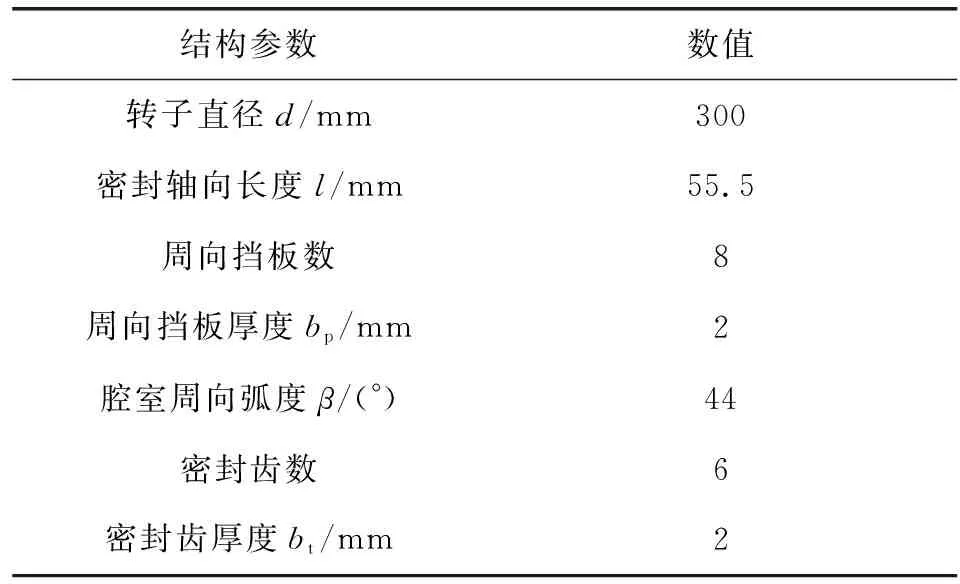
表1 贯通挡板袋型阻尼密封部分结构参数

结合该阻尼密封的实际工作环境，设置仿真输入参数如表2所示。

表2 贯通挡板袋型阻尼密封流域的输入参数

给出了计算过程中输入的轴颈涡动位移曲线如图7所示，相应的时域轴颈径向力相应曲线如图 8所示。由图 8可看出流场建立到稳定过程中流体力的变化，从第二个涡动周期开始，流场趋于稳定，轴颈受力周期性明显。此时以2种涡动下稳态过程中的周期力的傅立叶级数一阶谐波分量代入式(4)中，即可计算得到动特性系数。腔室中速度分布云图如图 9所示。文中所用腔室深度、宽度与密封间隙见表3。

图7 贯通挡板袋型阻尼密封流域的涡动位移信号

图8 贯通挡板袋型阻尼密封流域的响应力

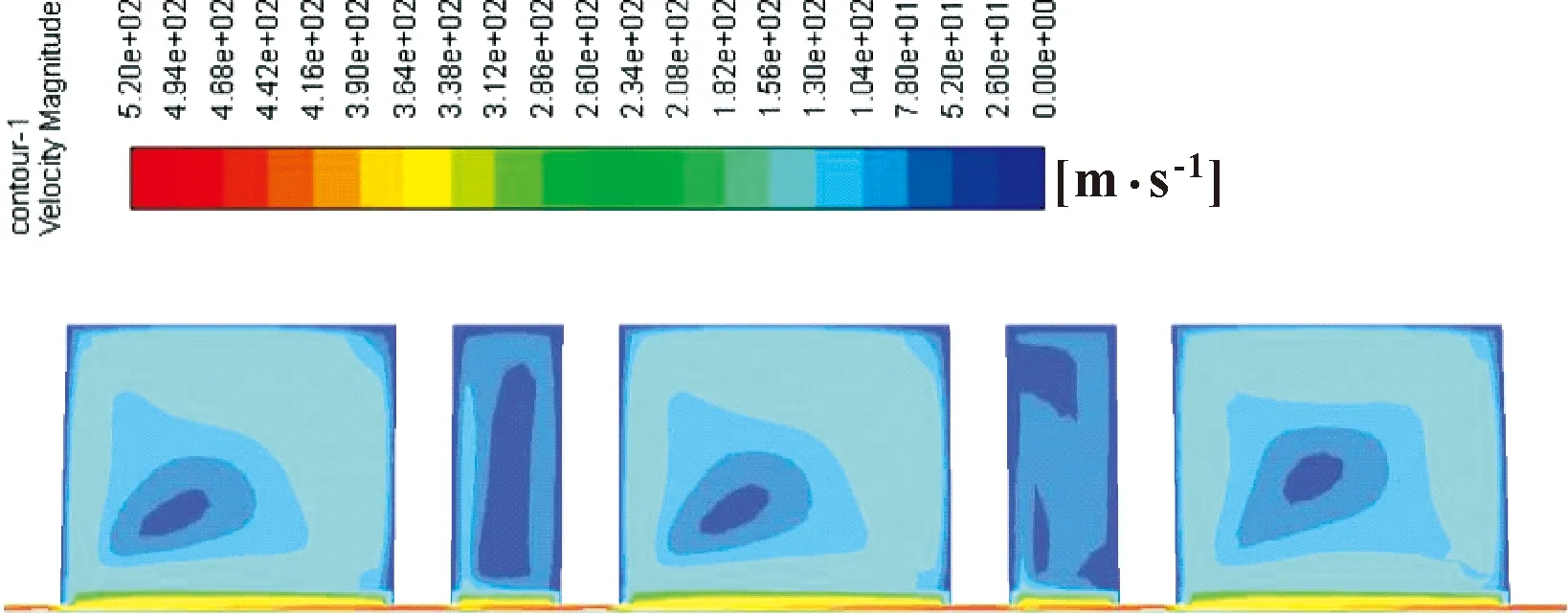
图9 袋型阻尼密封流域速度云图

表3 示例中贯通挡板袋型阻尼密封结构参数

2.2 腔室深度的影响

依次取腔室深度为4、5、6、7、8、9、10 mm，其他参数按表3不变，探究了腔室深度对贯通挡板袋型阻尼密封动力学特性的影响。

按照前述方法，求得了不同腔室深度下的动特性系数，如图 10、图 11所示。在所讨论腔室深度范围内，贯通挡板袋型阻尼密封的动特性系数均为正值。其中随腔室深度增加，直接刚度单调递增，直接阻尼单调递减；交叉刚度随着腔室深度的增大先增大后减小，交叉阻尼随着腔室深度的增大先减小后增大，均在腔室深度为6 mm左右时出现极值。

图10 腔室深度对贯通挡板袋型阻尼密封刚度的影响

图11 腔室深度对贯通挡板袋型阻尼密封阻尼的影响

图10中，直接刚度明显大于交叉刚度，在所述参数变化范围内，直接刚度的变化幅度(约700%)也比交叉刚度变化幅度(约300%)明显。图 11中，直接阻尼和交叉阻尼大小接近，但稍大；在所述参数变化范围内，两者变化幅度相仿。

2.3 密封间隙的影响

依次取密封间隙为0.1、0.15、0.2、0.25、0.3、0.35 mm，其他参数按表3不变，探究了密封间隙对贯通挡板袋型阻尼密封动力学特性的影响。

按照前述方法，求得了不同密封间隙下的动特性系数，如图 12、图 13所示。可以看出：在不同密封间隙下，贯通挡板袋型阻尼密封的动力学特性系数均为正值。在密封间隙大于0.1 mm时，直接刚度随密封间隙增大不断增大，直接阻尼随间隙增大不断减小；而交叉刚度和交叉阻尼均随着密封间隙的增大而先减小后增大，交叉刚度在密封间隙为0.25～0.3 mm时出现极小值，交叉阻尼在密封间隙为0.3～0.35 mm时出现极小值。

图12 密封间隙对贯通挡板袋型阻尼密封刚度的影响

图13 密封间隙对贯通挡板袋型阻尼密封阻尼的影响

另由图12、图 13可知，所讨论密封间隙参数范围内，直接刚度明显大于交叉刚度，直接阻尼和交叉阻尼大小接近，但稍大。

2.4 基本腔室宽度的影响

密封腔室宽度由密封轴向长度、齿数和齿厚决定。在实际的涡轮机械中，受安装尺寸和结构布局的影响，密封的轴向长度一般是给定的，此时齿厚越大、齿数越多，腔室宽度就会越小，反之亦然。由于对袋型阻尼密封而言，密封腔室对动力学特性起主导作用；且在袋型阻尼密封结构设计中，基本腔室宽度一般是二次腔室宽度的整数倍，因此文中将封齿厚度与基本腔室-二次腔室宽度比固定，通过改变密封齿数，讨论基本腔室宽度对贯通挡板袋型阻尼密封动力学特性的影响。

文中使用的若干组基本腔室宽度、二次腔室宽度、齿数的参数见表4。按照前述方法，求得了动特性系数如图14、图15所示。

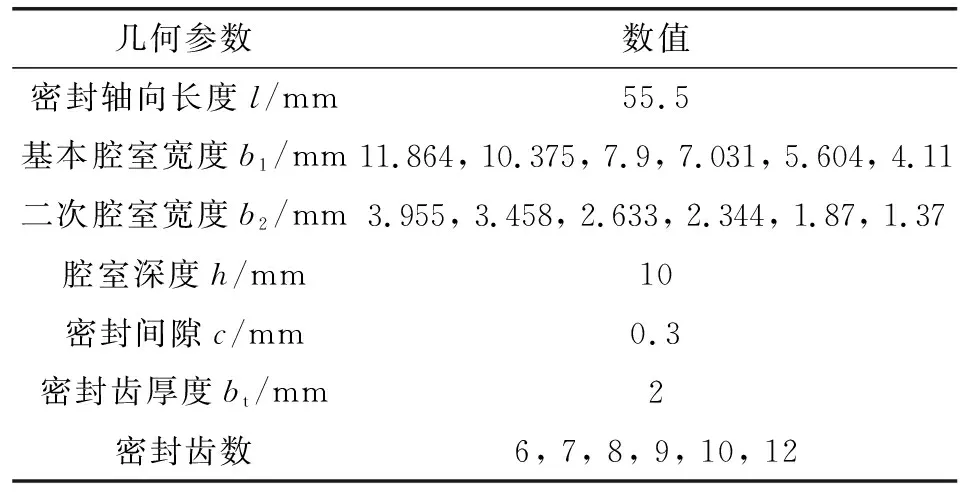
表4 计算所用结构几何尺寸

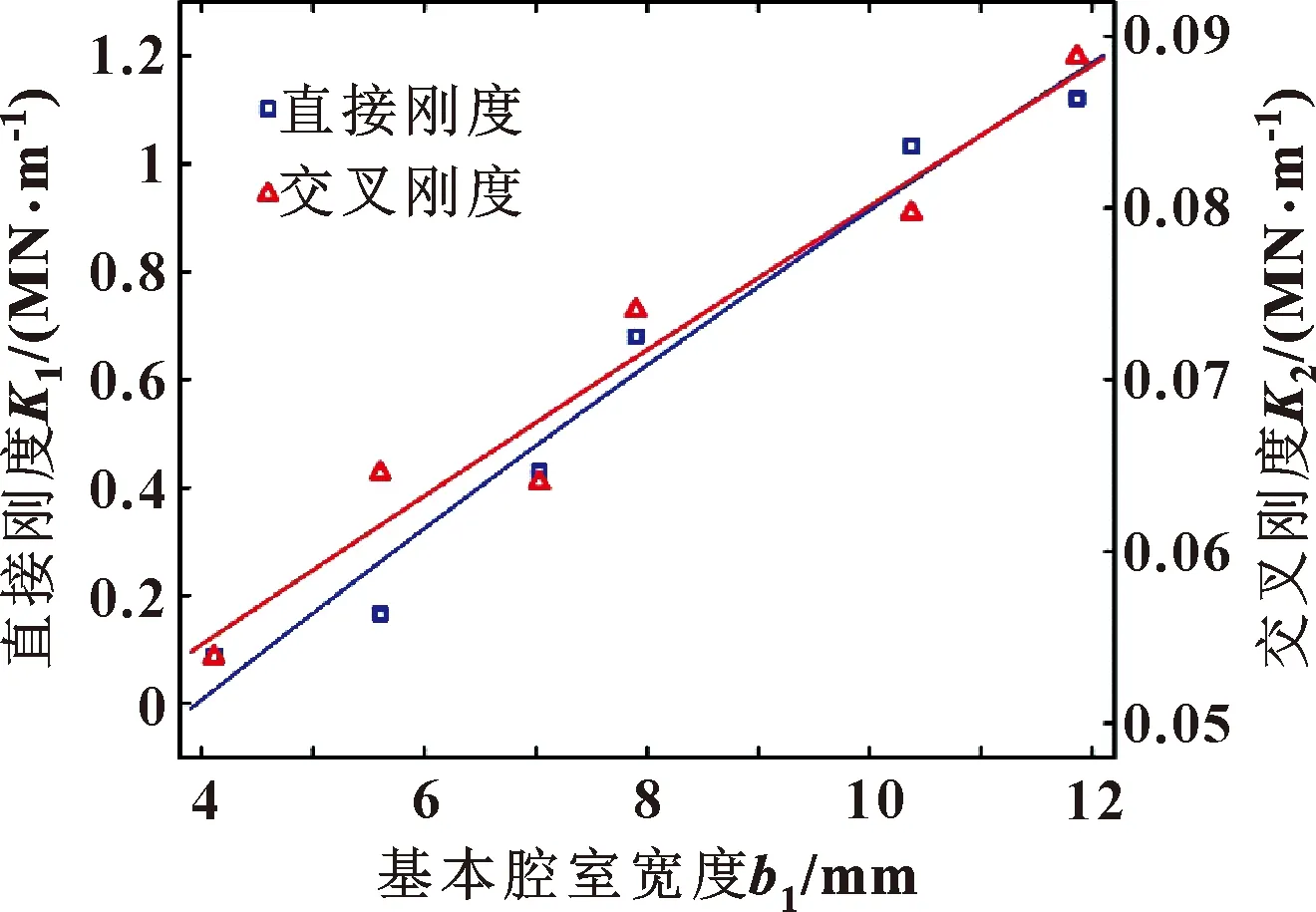
图14 基本腔室宽度对贯通挡板袋型阻尼密封刚度的影响

图15 基本腔室宽度对贯通挡板袋型阻尼密封阻尼的影响

从图14、图 15中可以看出：在所讨论基本腔室宽度范围下，贯通挡板袋型阻尼密封的动力学特性系数均为正值；随着基本腔室宽度的增大，直接刚度和交叉刚度均大致呈现线性增大的趋势，而直接阻尼和交叉阻尼均大致呈现先增大后减小的趋势；直接阻尼在基本腔室宽度为7 mm左右时出现极大值，而交叉阻尼在基本腔室宽度为9 mm左右时出现极大值。

另由图14中可以看出，腔室宽度进一步减小时，该型密封有产生负刚度的趋势。