基于BP神经网络的机器人力矩补偿研究

梁学胜，高伟强，许东伟，刘建群，郭俊权

(1.广东工业大学机电工程学院，广东广州 510006；2.佛山市智昂科技有限公司，广东佛山 528225)

0 前言

拖动示教以其简单直观、对操作者要求低等优点而广泛应用于喷涂、冲压等工业机器人中。拖动示教又称为直接示教，可以分为伺服级接通示教和功率级脱离示教[1]。后者需要伺服驱动器工作于力矩模式，然后由生产工人按照需求直接拖动机器人进行示教，生成机器人控制程序。这种示教方法操作简单，适用于需要面对复杂运动工况的工业机器人，但需要操作者施加较大的力来克服机械臂重力、惯性力等进行拖动示教，操作灵活性受到约束，难以获得平稳、准确的运行示教位姿。因此，如何对拖拽示教进行力矩补偿助力，成为该类示教机器人控制器设计的关键。

文献[2]提出机器人零力控制的概念，即机器人示教过程中仿佛处于不受重力和摩擦力的环境，并且GOTO[3]提出通过位置控制实现零力控制的方法。游有鹏等[4]提出基于力矩控制的零力控制方法，并给出基于自测量的重力矩和摩擦力矩计算方案。可以看出，这类方法在实际示教控制中需要进行机器人动力模型的实时解算。而机器人精确的动力学模型实时解算中获取机器人结构、运动等参数较为困难，且会大大增加算法耗时，这严重制约了这类运动控制算法在高速采样示教机器人中的应用。针对上述问题，本文作者针对拖动示教喷涂机器人，提出一种基于神经网络的机器人拖动示教力矩补偿方法：(1)分析多自由度机器人拖动示教过程中惯性力、重力等因素对各个关节力矩补偿的影响；(2)采用无监督学习的BP神经网络对算法模型进行训练，使用经过训练的模型来替代复杂的机器人动力学解算以提高算法的计算效率，实现算法在高速采样示教机器人中的应用。

1 机器人力矩补偿分析

力矩补偿需要对机器人整体进行动力学分析，通常，关节型机器人的动力学方程有如下表示[4-5]：

(1)

拖动示教喷涂机器人的总体结构如图1所示。可知：整个机器人的惯量主要分布于大臂和小臂，大、小臂关节的力矩计算是力矩补偿算法的关键部分。此外，该机器人跟常规的6DOF机器人相比，还增加了平衡气缸、连杆等辅助结构。因此，为保证算法的有效性，还需对大臂和小臂的力矩补偿进行修正。

图1 喷涂机器人总体结构Fig.1 Overall structure of spraying robot

1.1 喷涂机器人的力矩补偿算法

在力矩补偿算法中，为了降低算法耗时，阻尼力矩可以通过实验测试获得的一常数对角阵Cf来近似替代部分阻尼力，将剩下的部分以及式(1)中计算较为复杂且数量级较小的非线性耦合项交由操作者施加外力来克服。因此，关节电机应补偿力矩TJ可简化为

(2)

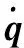
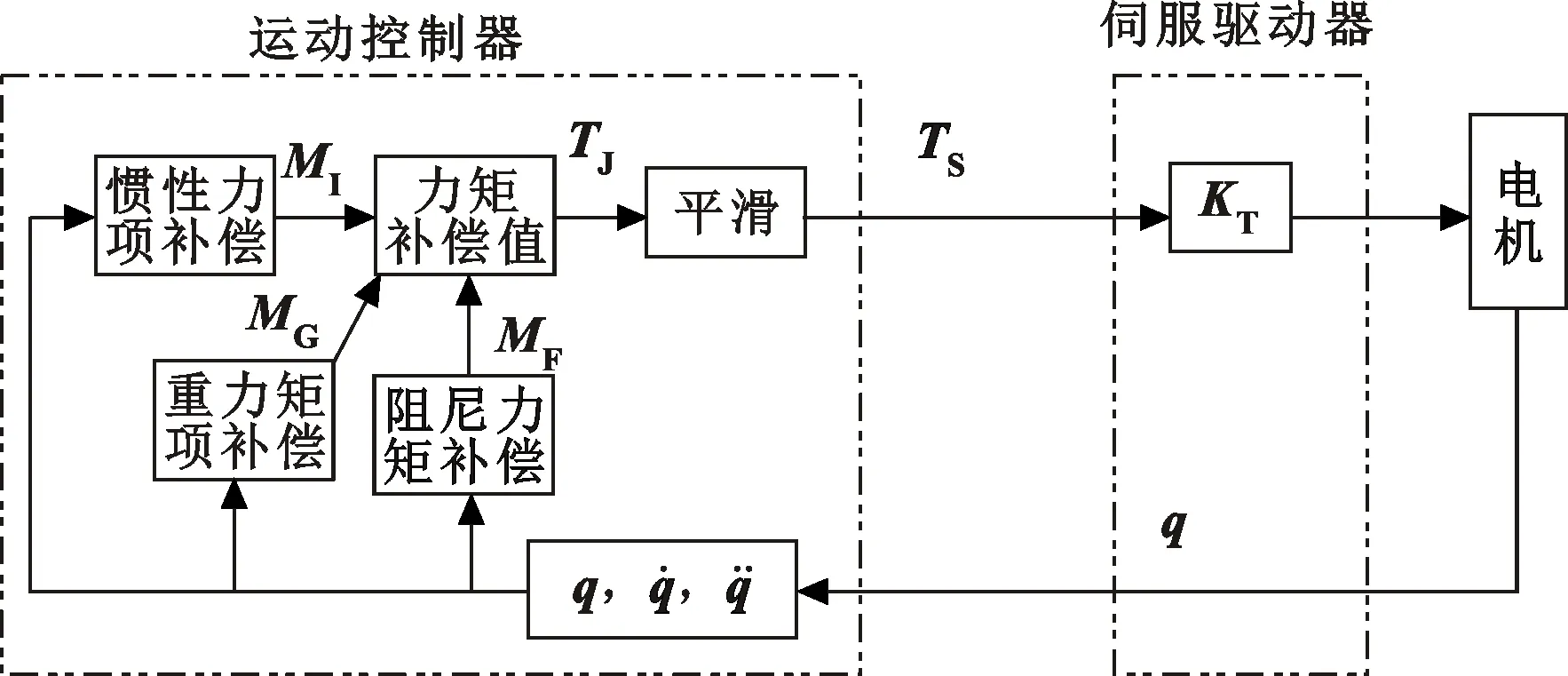
图2 力矩补偿算法流程Fig.2 Flow of torque compensation algorithm

1.2 针对小臂的力矩补偿

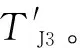
(3)

式中：T3为小臂平衡气缸产生的力对小臂关节产生的力矩。

连杆一AOB可看作是一刚体，F1为小臂平衡气缸产生的推力，其大小可以根据气缸压力设定值p1查询气缸理论出力表获得，可得

F1·d1=F3·OB

(4)

F2为连杆二中的推力，其大小等于F3在其方向上的分量，即

F2=F3·cosθ

(5)

联立可得，小臂平衡气缸产生的力对小臂关节产生的力矩为

T3=F1·d1·OB-1·cosθ·d2

(6)

图3 小臂机构受力Fig.3 Force analysis for forearm

1.3 针对大臂的力矩补偿

为了减小大臂关节电机的负载，机器人大臂两侧各安装有一个平衡气缸，通过产生同等的拉力来平衡整个机器人的重心，因此力矩补偿中需要减去这两个气缸产生的力矩。大臂机构受力如图4所示，点D为大臂平衡气缸支座，OD沿竖直方向，平衡气缸拉力方向与大臂形成一微小夹角α，β为大臂摆角。同时，还要考虑小臂平衡气缸对大臂力矩补偿的影响。因此，大臂力矩补偿值TJ2可修正为

(7)

式中：T21、T22分别为小臂平衡气缸和大臂平衡气缸对大臂关节产生的力矩。

由图3分析可得

T21=F1·d1

(8)

由正弦定理可知

(9)

因此可得

(10)

式中：F4为大臂两侧平衡气缸产生的拉力，其大小可以根据气缸压力设定值p2查询气缸理论出力表获得。

图4 大臂机构受力Fig.4 Force analysis for big arm

2 BP神经网络

上述力矩补偿算法中需要进行动力学模型计算，运算量较大，算法耗时高达数毫秒甚至是数十毫秒，无法应用于高速实时采样的示教机器人。

人工神经网络是一种模仿生物神经网络行为特征、进行分布式并行信息处理的算法模型，反向传播(Back Propagation，BP)神经网络被证明有良好的非线性函数逼近能力[7]。机器人的力矩补偿算法是复杂的非线性系统模型解算，利用神经网络的函数逼近来替代高运算量的机器人运动控制算法，是解决这类算法实时性问题的有效手段之一。

2.1 模型构建

使用的神经网络由输入层、隐藏层和输出层组成。这3层神经元个数分别为nI、nH、nO，各层神经元的索引分别用i、j、k表示。

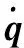
(11)

参考Kolmogorov定理并采用试凑法[8]，通过实验测试得到隐藏层的神经元个数nH为34时，算法模型有较好的收敛效果。根据神经网络的任务目标为函数逼近，选择隐藏层和输出层的激活函数为带泄漏的线性整流函数(LeakyReLU)，参数α为0.182[9]，该激活函数表达式为

(12)

BP神经网络由线性单元组成，需要训练的参数为ωi、bi、ωj、bj，分别是输入层和隐藏层中各个神经元的权重和偏置。设xi为输入层第i个神经元，隐藏层中第j个神经元的输出H(j)可以表示为

(13)

输出层中第k个神经元的输出Y(k)可以表示为

(14)

使用的神经网络模型如图5所示。

图5 三层BP神经网络Fig.5 Three layers BP neural network

2.2 模型训练

(15)

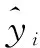
图6 神经网络模型训练过程

3 实验测试

为了验证力矩补偿算法和已完成训练的神经网络模型，下面进行实验以测试算法模型的精度、计算效率以及力矩补偿的有效性。

神经网络函数逼近精度可以通过数据测试集来验证。以大臂力矩补偿为例，将第二节中所得测试集代入BP模型中得到预测值，结果如图7所示。与文中第1.3节所述力学模型计算所得的理论值相比，平均误差为9%，最大误差为17%，BP模型预测值的分布和趋势与理论值一致，通过增加训练数据集样本数或增加模型训练次数，可以降低误差使该模型进一步实用化。

图7 神经网络模型效果Fig.7 Effect of BP neural network model

将训练好的神经网络模型移植到自研的基于EtherCAT总线的喷涂机器人控制器中进行拖动示教实验。实验平台采用IPC，控制器CPU为Intel i5 4200U。测试环境为Ubuntu 14.04，内核为基于Xenomai 3.1.0的实时内核，关节驱动采用EtherCAT总线伺服电机，实验机器人本体采用佛山某机器人公司喷涂机器人。使用Xenomai高精度内核时钟对算法的耗时进行测试，测试结果如表1所示。相比较可得:经过基于BP神经网络的算法将算法平均耗时减少70%，单个周期计算耗时小于3 ms，适用于高速采样的示教机器人。

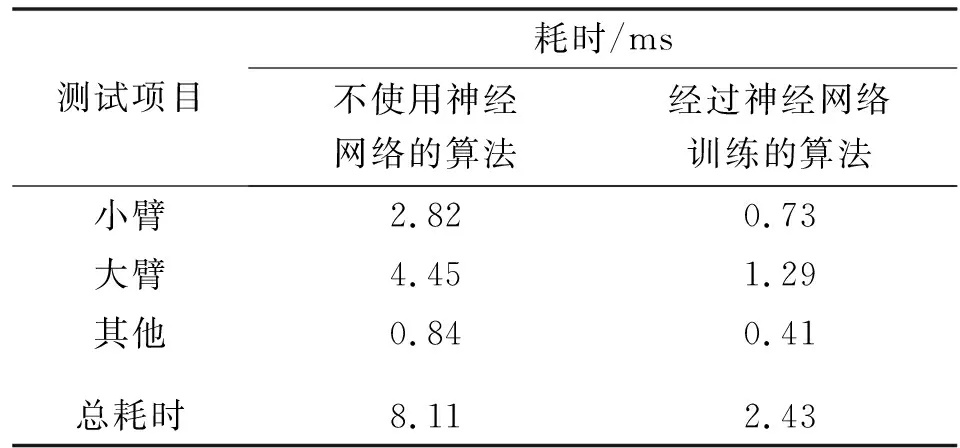
表1 力矩补偿算法单个周期耗时

最后由操作者拖动机器人末端进行示教，使用精度为±0.5%的测力计测量机器人静止状态下向前拖动机器人所需要的最小外力Fmin。实验现场如图8所示。无力矩补偿算法时最小外力Fmin为92.64 N，使用力矩补偿算法后为14.74 N。对机器人的各个方向进行10次拖动并测量最小外力，其平均值如表2所示。由此可得:力矩补偿效果明显，操作者可以轻松进行机器人的拖动示教。

图8 拖动实验现场照片Fig.8 Photo of the dragging experiment scene

表2 力矩补偿算法效果Tab.2 Effect of torque compensation algorithm

4 结束语

拖动示教喷涂机器人由于具有使用简单方便、示教喷涂效果所见即所得等优点，得到越来越多涂装企业的重视和推广应用。目前这类机器人最大问题之一就是拖拽力大、拖动示教灵活性差。解决这一问题的有效方法就是示教时，让关节的伺服驱动器工作于力矩模式，通过关节助力降低人工拖拽力，提高操控灵活性。

通过对拖动示教喷涂机器人建立力矩补偿动力学模型，提出将BP神经网络应用于拖动示教在线关节力矩补偿算法中，解决了补偿力矩高效实时的计算问题。该算法在自研的基于EtherCAT总线的机器人控制器中进行了有效性验证。所用的BP神经网络模型收敛速度快，计算效率高，函数逼近能力强。该模型经过训练后可以替代复杂的机器人动力学解算，有效提高算法的计算效率，为解决低采样周期中算法的实时性问题提供了参考。