食品搬运机器人小臂的静态分析与优化

韦洪新，王智森

（景德镇学院 机械电子工程学院，江西景德镇 333000）

0 引言

机器人作为一种新兴产业，近年发展势头十分迅猛，在我国生产行业中承担越来越重要的角色［1］。机器人由于精确度高、适应性强、稳定性好等优点逐渐获得企业的青睐［2］。在实际的生产制造当中，食品搬运是一项十分费时费力且重复性高的工作。在工业生产制造技术不断发展的过程当中，企业所需的人力成本逐渐增加，出现劳动力短缺的现象也越来越严重，食品搬运机器人由于它的种种优点可以很好地完成食品运输工作。由于食品搬运机器人的效率更高，对材料的利用率也高，可以大大地降低生产成本，企业扩大生产规模也变得更容易。这对推动食品工业生产制造产业发展壮大，提高产品质量，控制生产成本有巨大的作用。

我国对食品搬运机器人的研究起步较晚，与国外技术相比还存在一定差距。机器人的结构在设计的过程中，除了满足相应的强度、刚度和工作受载条件外，还应当尽量轻便，提高机器人节约材料，实现优化等效果。近年来，我国研究人员对食品类机器人进行了相关研究。为满足单体食品在搬运过程中的自动化分拣，蒋毅等［3］采用ADAMS和SimDesigner方法对机器人虚拟样机进行了分析，为机械臂的设计和驱动电机的选择提供了参考。针对食品包装箱码放的实际要求，陈亚琳［4］采用ADAMS软件和D-H法对机器人的选型及控制系统的设计提供了理论依据。赵相博等［5］对食品冷藏箱码垛机器人进行了路径规划，利用直线和插值多项式，为机器人在搬运中各点的位置准确性提供了技术支撑。本文在SolidWorks中建立食品搬运机器人小臂的三维模型，通过分析计算求出小臂的受力情况，并进行有限元静态分析，在此基础上进行形状优化设计。

1 食品搬运机器人的结构分析

食品搬运机器人的结构主要由传动轴、大臂、法兰、小臂、连杆等主要部件及附属零部件组成，整体模型如图1所示。其中底座起支撑作用，大臂通过连杆传动轴和小臂箱体分别与连杆和小臂相连，承受驱动臂座以上载荷。小臂左端与小臂箱体连接，右端与前爪法兰相连。腕部中心轴为末端执行器，通过旋转法兰和前爪法兰将所受载荷传递给小臂。

图1 食品搬运机器人Fig.1 Food handling robot

小臂是连接机器人抓手与大臂的关键部件，其强度和刚度对机器人的工作精度有直接影响。因此，研究食品搬运机器人小臂的受力状态，优化结构设计对机器人提高整体性能具有十分重要的作用。

2 小臂的结构与静态分析

2.1 几何模型的建立

ANSYS软件在处理结构的力学等分析中具有强大的处理功能，但在几何模型的构建中存在一定的不足，比较繁琐。三维模型的建模中常用的软件有UG、Pro E、SolidWorks等，本文选择SolidWorks软件对食品搬运机器人的小臂进行实体建模。在模型的构建中，保证强度和刚度的同时，忽略与分析影响不大的细节，如小的倒角、螺纹孔等［6-7］。将建立好的模型保存为.x_t格式，并将其导入到ANSYS Workbench中。

2.2 小臂的有限元模型

小臂的材料选择硬质铝合金，相关的材料属性：密度2 780 kg/m3，泊松比0.29，弹性模量6.9×104MPa，抗拉强度 370 MPa，屈服强度 125 MPa。单元类型设置为SOLID187，在划分技术中选择自由网格，同时设定网格单元尺寸为10 mm，将相关参数输入到分析软件中，生成164 663个节点，235 948个单元，划分后的有限元模型如图2所示。

图2 小臂的有限元模型Fig.2 Finite element model of forearm

2.3 分析载荷受载情况

食品搬运机器人在工作时，小臂的受力情况随其他零部件结构位置的改变而变化。经分析可知，当小臂与小臂箱体、前爪法兰、手腕旋转法兰及腕部中心轴处于水平位置，即图1所示位置时，小臂所承受载荷量最大，产生的变形和位移最大。在对小臂进行静态分析时，以此时的受力状态为研究对象。由原始设计参数可知，机器人所能抓取的最大载荷为90 kg，小臂右端零部件的总质量为22 kg，在计算时将右端物体和零部件视为刚体，简化为施加在小臂右端的力F物和力矩M1，小臂的质量为51.8 kg，其重心位置距离大臂335 mm，机器人的受力及结构尺寸简图如图3所示。

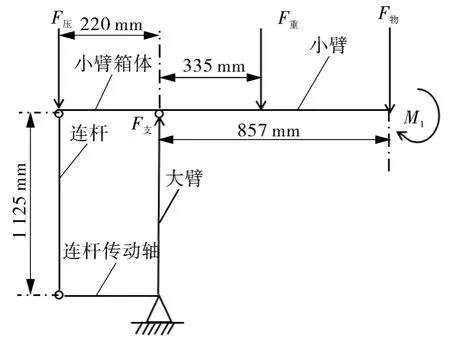
图3 食品搬运机器人结构受力简图Fig.3 Structural stress diagram of food handling robot

根据材料力学中力和力矩平衡公式可得以下方程：

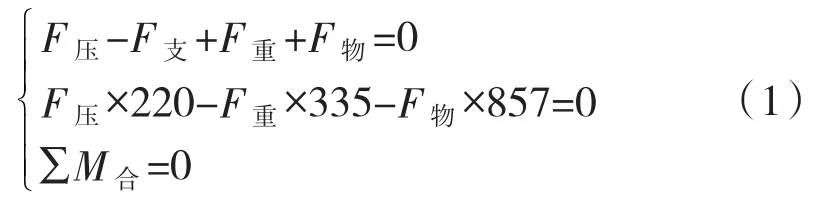
将已知条件代入式（1）可求出相关未知量，大臂所承受的支撑力为6 656.8 N，小臂箱体左端的压力为5 050.8 N。此时，可将小臂箱体左端压力分解为施加在小臂左端的力和力矩。机器人小臂结构的受力简图如图4所示，其中力矩M2的大小为2 272.9 N·m。

图4 受力简图Fig.4 Force diagram

2.4 应力与应变求解

由上述对小臂的载荷分析和受力情况，在ANSYS Workbench中输入相关载荷及位移约束，并进行结果后处理［8］。总的变形云图和von-Mises应力分布云图分别如图5和图6所示。

图5 小臂总变形云图Fig.5 Total deformation nephogram of forearm

图6 小臂应力云图Fig.6 Stress nephogram of forearm

从图5可知，小臂在承受最大载荷时的总的变形量为0.338 mm，最大变形量发生在小臂右端与前爪法兰连接位置。与小臂总长相比，变形量很小，可以满足食品搬运机器人在工作时的精度要求。从图6可知，小臂所受应力较小，最大应力为9.68 MPa，主要集中在左端小臂套筒与直径连接最外侧部分，由于硬质铝合金的屈服强度为125 MPa，所以小臂的强度满足设计要求。

3 拓扑优化

3.1 拓扑优化的理论根据

在数学模型处理中，一般的优化问题可由下式获得：minV（x）

式中V（x）——目标函数；

ximax，ximin—— 优化变量取值的最大值和最小值；

xi——优化变量；

i——优化变量的数量；

Gj，Hk——约束函数；

j——不等式约束的数量；

k——等式约束的数量。

对于连续体结构引入柔顺度函数C，C取值越小，结构越稳定，刚度越大［9］。函数C：

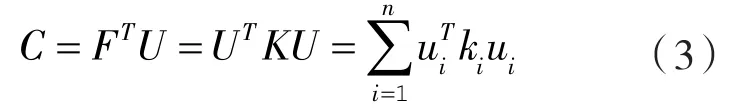
式中F——结构载荷；

U——位移量；

K——刚度矩阵；

ui——单元位移矩阵；

ki——单元刚度矩阵。

代入中间密度惩罚模型公式：

式中xi——相对密度；

E0——弹性模量；

p——惩罚因子。

对于插值单元，惩罚后的刚度矩阵k（xi）关系式：

式中k0——密度为1单元刚度矩阵；

f——隐函数映射关系。

通过式（2）、（3）、（5）联立，求出以质量为约束的拓扑优化模型公式（6）。

其中，f为各参量间的隐函数关系，M（xi）为最终优化的质量，M0为原始质量，M*为设定质量允许的最大值，mi为单元质量，gj为可能存在的不等式约束，hk为可能存在的等式约束，ximax，ximin指相对密度的上下限。

由上述理论基础，在ANSYS Workbench中选择拓扑优化分析，优化分析流程如图7所示，优化空间的选取结合实际情况选择应力较低且在设计中便于装配调试的区域。

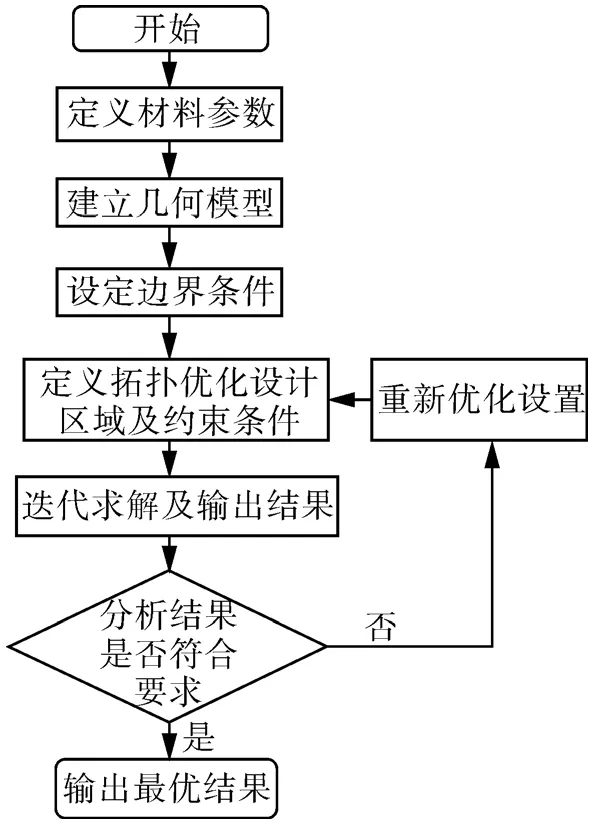
图7 拓扑优化流程图Fig.7 Topology optimization flow chart

3.2 小臂的拓扑优化

小臂在整体连接时大部分为实体材料，结构存在很大的优化空间。利用ANSYS Workbench软件自带的形状优化模块功能，基于前面的静态分析，原有的网格划分设置和受力情况不变，在形状优化模型求解中，设置小臂的质量减少20%为优化目标［10］。完成分析计算后可以得到满足初始条件的优化结果图8，图中浅色部分为不建议去除部分，深色部分为建议去除部分。建议去除部分主要分布在2个地方，一为小臂的两侧及中心轴处，一为小臂套筒右端圆角处。其中，沿水平方向的小臂两侧边的深色部分全长分布，其他方向分布很少。

图8 优化结果Fig.8 Optimization results

综合考虑小臂的实际使用情况和形状优化结果，小臂套筒右端圆角及附属零部件和小臂圆轴中心处可以考虑减重。经多次反复计算分析，可将小臂套筒圆角设定为35 mm，小臂中心轴切除直径值为80 mm，优化后的小臂模型如图9所示。对重构后的小臂模型再次静态分析，可求得总变形云图和应力云图分别如图10和图11所示。

图9 优化后的小臂模型Fig.9 Optimized forearm model

图10 优化后总变形云图Fig.10 Total deformation nephogram after optimization

图11 优化后应力云图Fig.11 Stress nephogram after optimization

优化前后的结果对比如表1所示，对优化后的小臂进行分析，可以得出以下结论：从图10可知，小臂的最大变形量仍然很小，为0.349 mm，与优化前0.338 mm相比变化率增加了约3.2%，位移变形量不大，能够满足机器人作业要求；从图11可知小臂的最大应力值为8.60 MPa，远低于硬质铝合金材料屈服强度125 MPa，与优化前9.68 MPa相比减少了约11.2%，有充足的安全余量；在刚度和强度均满足于设计要求条件下，小臂质量由原来的51.8 kg减少为现在的41.6 kg，减轻原有质量的约19.7%，达到了轻量化的设计要求。综合分析可知，除小臂位移量发生较小增加外，最大应力和质量均有较大的减少，优化后的整体结构满足设计性能要求。

表1 小臂优化前后的性能对比Tab.1 Performance comparison of forearm before and after optimization

4 结语

以食品搬运机器人小臂为主要研究对象，对小臂进行研究，建立机器人的三维模型，确立其危险工况时小臂的受力情况。通过ANSYS Workbench对小臂进行静力学分析和拓扑优化，获得相关分析数据。以实现机器人小臂的轻量化为目标，结合拓扑优化分析和实际制造工艺及加工装配的影响，对小臂结构进行优化。结果表明：经过轻量化设计后，小臂的质量减轻了19.7%，与此同时，小臂的刚度得到提升，小臂的强度在合理的变形量内。该优化方法为食品搬运机器人同类其它产品和相关结构的设计提供理论参考，为其他结构的优化设计提供相关经验。