深埋矿体采场爆破对矿柱的损伤特性研究

张翔宇,严 鹏,卢文波,张立新,宋 亮,陈 明

(1.武汉大学 水资源与水电工程科学国家重点实验室,武汉 430072;2.武汉大学 水工岩石力学教育部重点实验室,武汉 430072;3.五矿矿业控股有限责任公司,合肥 230091)

中国新型工业化、城镇化、信息化和农业现代化建设对矿产资源和能源的刚性需求巨大，且仍将长期保持高位态势[1]，而经过数十年高强度的开采，我国浅部露天矿陆续闭坑，地下开采矿山比重不断增加。

地下矿山开采大规模使用的是房柱法或房柱嗣后充填采矿法，回采过程中，通过预留矿柱支撑上部岩体以保证采场结构的稳定，因此矿柱的稳定事关矿山生产安全，一旦失稳，将导致采空区顶板坍塌，威胁矿工安全，甚至造成更为严重的事故，矿柱的稳定性是地下深埋矿山安全开采的先决条件[2]。针对矿柱的稳定性，国内外学者指出深部采场爆破开挖损伤是地应力(静)与爆炸应力(动)共同作用的结果[3]，实际采场爆破产生的损伤对矿柱的安全稳定具有一定影响。Kaiser等[4]研究表明深部矿体爆破开挖过程中，由于爆破开采速率快，动应力增加将导致矿柱失稳破坏；Zhou等[5]通过研究矿柱爆破回采时相邻矿柱产生的动力响应，指出受爆破动荷载的影响将会触发较为强烈和大范围的矿柱坍塌，爆破扰动对矿柱的影响不可忽视；Huang等[6]研究表明尽管微差爆破(爆破优化)可以减少爆破振动对矿柱的影响，但爆炸荷载对矿柱的影响仍然不可忽略，容易使深部薄矿柱更易失稳。严鹏等[7]同样指出爆破设计的优化及控制爆破的采用只能减小爆破荷载产生的爆破损伤，无法消除爆破损伤，故深部采场爆破对矿柱造成的损伤需深入研究。

然而目前对矿柱的研究主要从力学机制、敏感性因素和数值模拟等方面进行其稳定性分析，这些计算方法中均未考虑采场爆破损伤对矿柱稳定的影响。如Huang等建立基于弹性薄板理论的力学分析模型，利用能量变分方法，推导了屈曲应力和长径比的关系，并将其用于地下开采薄矿柱的稳定性评价；谢学斌等[8]根据矿壁和充填体的联合承载机理，建立了矿壁受横纵荷载作用的稳定性分析模型，并对冬瓜山铜矿开采进行了分析验证；宋卫东等[9]采用正交试验，从矿柱宽度、开采深度和矿房宽度等方面对影响矿柱稳定性的因素进行了敏感性分析，得出保证安全开采的矿柱最小尺寸；徐文彬等[10]针对和睦山铁矿采空区垮塌现象，采用数值模拟建立了围岩失稳演化模型，并对其破坏机理进行了分析；Jaiswal等[11]利用三维有限元法(3DFEM)，将围岩视为应变软化材料，研究矿柱应力应变之间的关系，指出矿柱峰值强度与宽高比及单轴抗压强度具有一定相关性。例如矿柱稳定性计算方法中，常用公式(1)[12]计算矿柱承载强度σc(σR、B、H、V分别代表矿石单轴抗压强度、矿柱宽度、高度和体积，c、d为系数)。

σc=σR(B/H)cVd

(1)

式(1)表明保持矿柱形状规格不变，矿柱强度与矿石单轴抗压强度有直接关系。林斌等[13]在378组岩石(6类岩石)样本的试验中表明，岩石单轴抗压强度与其弹性模量成正相关关系，而弹性模量与声波波速的变化具有直接关系，声波波速的下降导致岩石弹性模量的降低[14]，目前工程上常用声波波速降低率表征岩体受爆破损伤的影响程度。由此可知，采场爆破对矿柱产生的爆破损伤将直接导致矿柱部分区域单轴抗压强度σR的降低，进而影响整个矿柱的计算强度(σc)。

综上可知，现有的矿柱稳定性分析中，未考虑高地应力与爆炸荷载共同作用下的矿柱损伤效应，往往高估矿柱的承载能力，增加采场作业的风险性。因此，有必要深入研究采场爆破对矿柱造成的损伤特性，探讨高地应力与爆破荷载相互作用的机理，为矿柱的稳定性分析提供必要的计算前提。本文以陈台沟深埋矿体开采为背景，基于ANSYS/LS-DYNA建立扇形孔爆破三维数值模型，研究深部采场爆破对矿柱的损伤特性，从理论与数值模拟角度解释爆破荷载与地应力相互作用的关系，为矿山安全开采提供技术支撑。

1 工程概况

陈台沟铁矿位于鞍山市北东11 km的千山镇，矿区距鞍千公路1 km，铁矿总资源量12.74亿t，共有5条矿体，主矿体Fe1走向长2 600 m，倾向北东，倾角68°～75°，平均厚度170 m，矿体控制标高-650～-1 670 m。设计年产量1 100万吨/年，采用分段凿岩阶段空场嗣后充填采矿方法，双中段(-780 m与-1 020 m)同时开采。通过对陈台沟铁矿现场取样(图1)并进行室内试验，得到矿岩物理力学试验参数，见表1。

表1中：ρ为岩石密度；Vp为岩石声波波速；fc为单轴抗压强度；ft为抗拉强度；μ是泊松比；E是弹性模量；φ为摩擦角；C为黏聚力。

矿体一期开采时，拟定采场结构参数(矿房矿柱尺寸)为20 m×80 m×80 m，高度方向25 m、25 m、30 m进行分段凿岩爆破，单盘区立面图如图2所示。先一步回采矿房，回采结束后充填、养护，然后二步回采矿柱。中深孔落矿，具体参数如下：采用Simba1354型液压凿岩台车凿扇形孔，炮孔直径80 mm，边孔角40°，此后每隔8°布置下一个炮孔，孔深7.1～26.4 m，堵塞段长度分别为2 m，3 m间隔布置，孔底距2.5～6.1 m，采用孔底起爆，孔底与矿柱边界留有0.7 m安全距离。

(a) 单轴压缩试验前后对比

表1 岩石力学参数Tab.1 Mechanical parameters of rock mass

图2 盘区立面布置图(m)Fig.2 Panel elevation layout (m)

2 数值模拟模型

2.1 计算分析模型

实际开采过程中，扇形孔数量多，孔深长，工程岩体尺寸较大，常采用多排分批次爆破，若采用全过程扇形孔爆破开采数值模拟，对网格划分和计算机性能要求高，且计算时间长，计算过程会因网格过度畸变而中断，因此本文计算模型取凿岩爆破第一排，排距1 m，取采场中段矿体进行计算，微差时间为50 ms。①～⑥依次起爆。为方便后续分析，将矿房矿柱交界面处分为上、中、下三个区域，如图3，炮孔参数见表2。

研究不同埋深对采场爆破的影响，以陈台沟铁矿-780 m埋深地应力水平为参考，其实测地应力水平σx=19.26 MPa，σy=16 MPa，水平地应力与自重应力近似相等，故以静水压力为研究标准。而-1 020 m埋深最大地应力为35 MPa，根据两者不同埋深进行线性插值，得到不同埋深开采的地应力水平，具体地应力加载工况分别见表3和图3，除爆破开挖面为自由边界外，其它边界条件均为无反射边界。

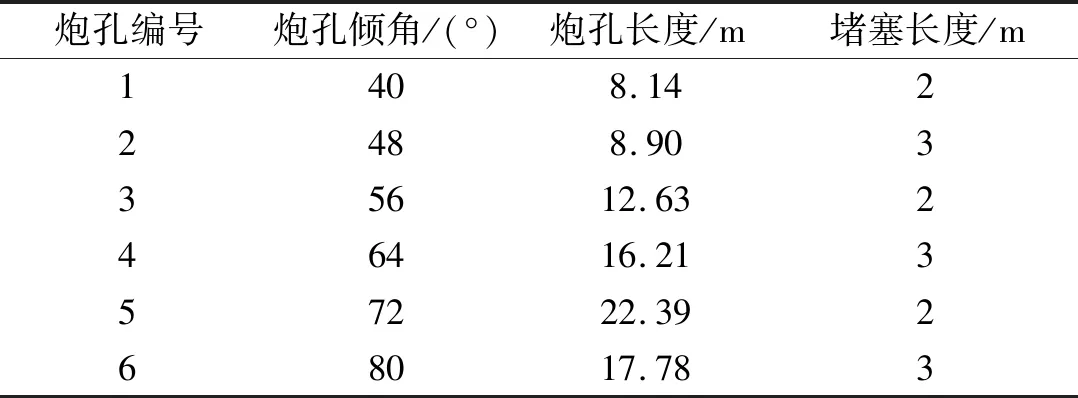
表2 炮孔参数Tab.2 The parameters of blast holes

表3 地应力加载工况Tab.3 In situ stress loading conditions

图3 计算模型Fig.3 Computational model

2.2 材料本构模型

Riedel等[15]提出的(Riedel Hiermaier Thoma)RHT模型广泛用于混凝土、岩石等脆性材料的损伤计算[16]，该模型考虑了三维应力空间中的强度特性，能较好反应岩石等材料在高地应力情况下的力学性能，通过引入失效面、弹性极限面和残余应力面来控制材料破坏[17]。

RHT模型中，失效面(σfail)是标准化静水压力、Lode角和应变速率的函数。其失效面方程可表示为

(2)

Borrvall和Riedel[16]提出3P*≥Fr时

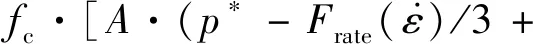
(3)

李洪超等[18]指出在三轴压缩试验条件下，拉压子午面参数Q0、B对三轴压缩试验条件下的应力应变曲线没有影响，参考文献[19]得Q0、B的参数为0.68和0.05。

Q=Q0+BP*

(4)

在RHT本构中，采用典型的p～α状态方程描述静水压力、材料密度和内能之间的关系，如式(5)。

(5)

其中：

(6)

(7)

(8)

B0=B1=γ0=2s-1

(9)

T2=0

(10)

(11)

(12)

式中：A1A2A3T1T2为材料参数；ρ0为材料初始密度；c0为纵波波速；s，γ0为系数，取B=B1=1.22。通过表1中的实测物理力学参数，计算得A1=T1=80.63 GPa,A2=98.34 GPa,A3=20.67 GPa，βc=0.009，βt=0.012。

材料孔隙开始压碎时的应力为pel，为2/3倍的单轴抗压强度，近似取pel=100MPa。损伤系数D由累积损伤应变和失效应变决定。其中：

(13)

(14)

当D=1时，表示材料完全损伤，D=0时材料未损伤，D1，D2是材料系数。

本文依据室内试验得到计算所用的部分参数，因所测岩石的单轴抗压强度、抗拉强度等与Xie等[19]的RHT模型参数近似，故剩余参数参考文献[19]，具体取值如表4所示。

表4 岩石RHT模型参数(kg,m,s)Tab.4 Parameters of RHT model for rock(kg,m,s)

炸药材料模型选取LS-DYNA软件内置*MAT_HIGH_EXPLOSIVE_BURN的炸药模型，采用Jones-Wilkins-Lee(JWL)状态方程来模拟炸药爆轰过程，状态方程如下

P为Chapman-Jouguet爆轰压力，V为相对体积；E0为初始能量密度,取2.39 GPa；Ap，Bp，R1，R2和ω为描述JWL方程的独立常数[20]。炸药参数见表5[21]。

2.3 参数验证

本文计算所需部分参数未能通过实验测得，表4所列参数是否适用于本文计算仍有待分析，故该节以陈台沟-780 m埋深巷道开挖后的声波测试结果验证分析表4的参数在本工程中的适用性。

表5 炸药参数Tab.5 The explosive parameters

陈台沟-780 m巷道开挖过程中，在巷道两边分别钻设声波孔，声波孔按顺时针编号，如图6所示，1#和4#孔下倾15°，2#和3#孔下倾45°，孔深10 m，现场实测声波孔见图4，声波测试结果见图5(其中2#孔测试时发生塌孔，因此数据中未有2号声波测试孔)。以声波波速降低率大于10%表征岩体损伤，图5表明，-780 m高程的1#、3#和4#测孔损伤深度为1.4 m、0.8 m和1.2 m，而图6中数值模拟损伤深度约1.05 m，由计算结果可知，实测损伤深度与数值模拟损伤深度误差较小，使用表4中的参数可以良好反映陈台沟深部岩体开挖的岩石条件。

图4 声波测试孔Fig.4 Sonic test hole

图5 声波测试结果Fig.5 Sonic test results

图6 实测与数值模拟对比结果Fig.6 Comparison results of actual measurement and numerical simulation

3 扇形深孔爆破损伤模拟分析

3.1 应力平衡分析

深部采场爆破考虑地应力作用时，采用重启动技术，将计算分为两个阶段，第一阶段为地应力平衡阶段，二阶段为爆破损伤计算。通过在模型边界上施加地应力荷载，待地应力平衡后，利用*STRESS_INITIALIZATION关键字实现第二阶段计算中对第一阶段应力、位移等计算结果的继承，进而模拟高地应力条件下爆破损伤。本文选取模型的第三主应力(最大压应力)分析，取静态地应力平衡后单元的应力时程曲线(图7)，论证炸药起爆前模型的应力情况。分析最大压应力可知，在炸药起爆前(300 ms时刻)，模型应力状态已达平衡，且不再产生应力震荡，可以进行高地应力条件下爆破损伤计算。

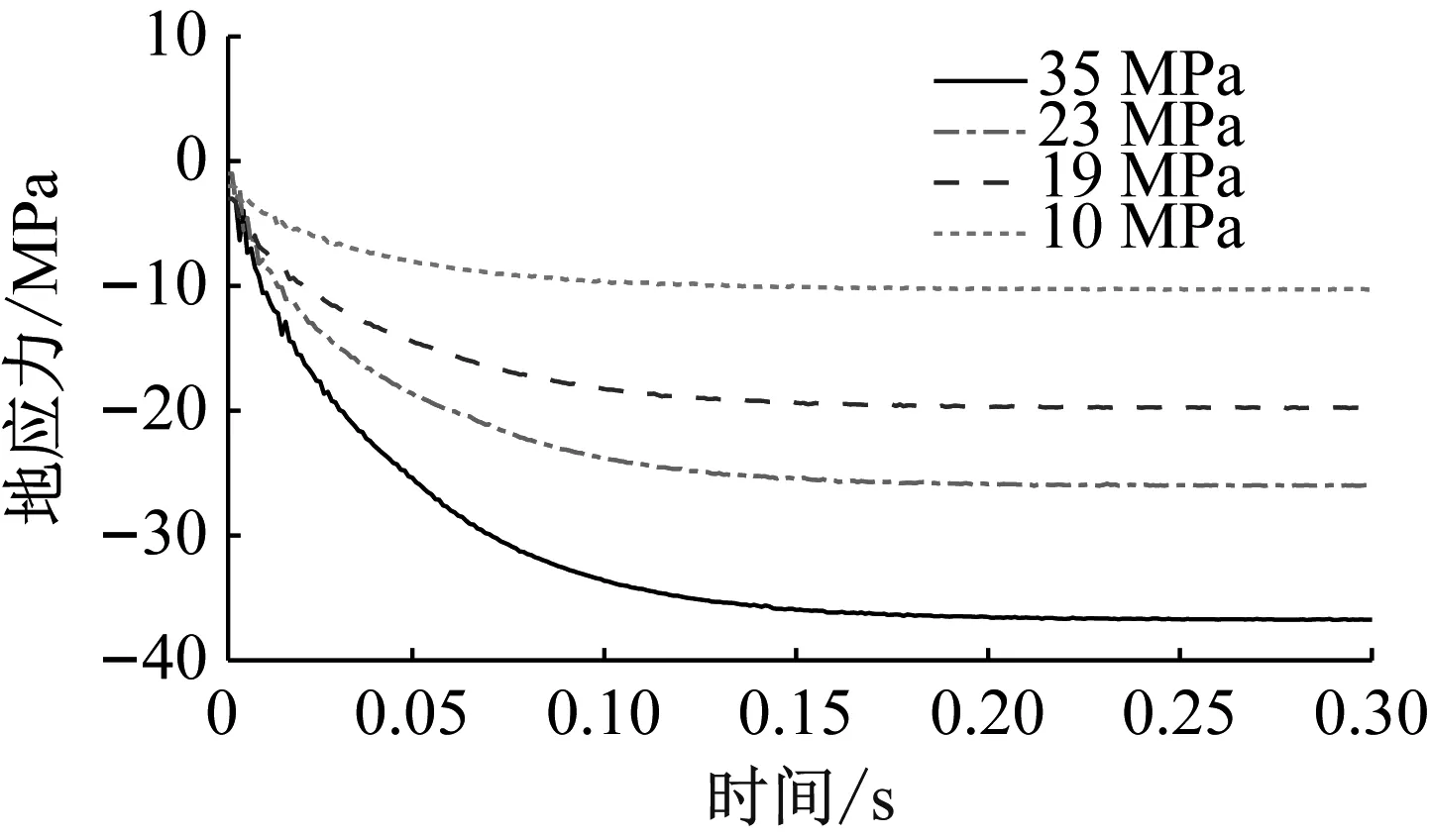
图7 地应力平衡应力时程曲线图Fig.7 the time history curve of in situ stress equilibrium

3.2 采场爆破损伤计算

为对比分析不同地应力条件下采场爆破对矿柱的影响，首先计算无地应力场矿房矿柱的损伤形态(图8)。

图8 无地应力条件下矿房矿柱损伤形态Fig.8 Damage morphology of room and pillar without in-situ stress

在无地应力的条件下，沿矿房高度方向，损伤布满整个矿房计算中段；沿矿柱深度方向，爆破损伤由矿柱中部向外辐射发展，在矿柱中部区域爆破损伤深度最小，损伤深度为1.30 m，上部损伤深度较大，最大损伤深度为1.74 m，在矿柱上部区域与下部区域，损伤深度均大于中部区域。

扇形孔爆破开采过程中，考虑不同静水压力作用下采场爆破对矿柱的影响，将表3中的工况进行计算分析，不同工况下的矿柱损伤如图9，统计矿柱不同区域的最大损伤深度如表6，绘制不同地应力条件下矿柱的损伤深度变化，如图10。

对比图8与图9可知，在地应力水平较低时(0～10 MPa)，矿柱中部区域具有一定程度的损伤内凹区，随着静水应力场的增大，矿柱上部与下部损伤深度衰减较快，其衰减趋势相同，而中部损伤内凹区的矿柱爆破损伤衰减较慢，即由于不同的装药结构及装药密集程度，地应力对矿柱不同区域的爆破损伤影响程度具有一定差异性；无地应力水平作用时，矿柱上部与下部损伤深度较大，随着地应力水平的增加，损伤深度较大区域衰减幅值较大，损伤深度较小区域衰减幅值较小，地应力水平达20 MPa左右时，上中下3个区域的损伤深度基本一致，矿柱受爆破损伤的影响区域变得更加均匀，此时爆破损伤基本在矿柱表面(约0.5 m)，扇形孔爆破对矿柱造成影响逐渐减小，但扇形孔爆破产生的损伤无法消除，其存在对矿柱的稳定性势必存在一定影响。

表6 不同工况下损伤深度Tab.6 Damage depth under different working conditions

(a) 10 MPa(-440 m)

图10 矿柱损伤深度变化Fig.10 The variation of pillar damage depth

3.3 爆破荷载与地应力相互作用关系

本文计算过程中，扇形孔数量多，炮孔长度不一，炮孔距不同，难以定量分析地应力对扇形多孔爆破的影响，但若仅考虑爆炸荷载与地应力相互作用的关系，定性分析爆炸荷载随地应力变化而变化的趋势，可以近似将炮孔中心面处应力变化简化为平面应变模型。故本节近似以厚壁圆筒模型进行简化，如图11。首先从理论层次分析爆炸荷载与地应力相互作用的关系，然后通过数值模拟分析炮孔周围的应力场变化，最后以矿柱区域的应力场进行验证，探讨不同地应力水平对矿柱爆破损伤的影响。

假设厚壁圆筒内外径分别为r和R，受内外压分别为q1及q2。

内外的应力边界条件为如式(15)所示

图11 厚壁圆筒受力示意图Fig.11 Stress conditions of thick-wall cylinder

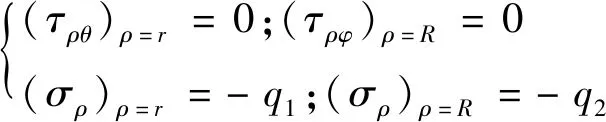
(15)

极坐标下圆筒受均布压力的一般解如式(16)

(16)

对于开挖后的深埋隧洞，认为R趋于无穷大、q1为0、q2为地应力，则开挖后的二次应力场为

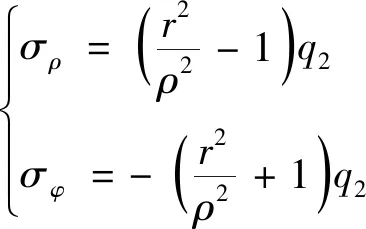
(17)

对于无初始应力场的隧洞，内壁受爆炸荷载时，认为R趋于无穷大、q1为荷载峰值、q2为0，则爆炸荷载诱发的二次引力场可表示为

(18)

对于弹性体，多应力场可线性叠加，故深埋隧道在有内荷载的情况下二次应力场可表示为

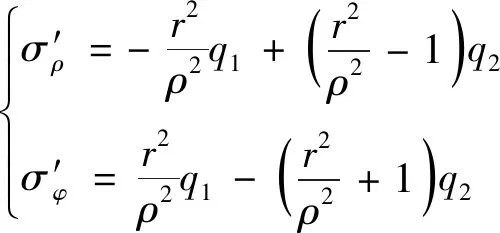
(19)

式(19)中拉为正，压为负，ρ≥r，地应力q2与爆炸荷载诱发的径向压应力符号相同，与环向拉应力符号相反，其存在增加了径向压应力峰值，抑制了爆炸荷载作用在孔壁上环向拉应力峰值。

耦合装药时，透射入岩石中冲击波的初始压力P为[22]

(20)

(21)

式中：ρG和ρ0为炸药与岩石密度；D为炸药爆速；c0为岩体声波波速；k为透射系数[23]。计算k=1.65，按照表5中乳化炸药参数进行计算得透射入岩体内部的爆破荷载峰值为5.96 GPa，较埋深780 m时(约19 MPa)的地应力，近似认为地应力对炮孔周围的径向压应力影响可以忽略。

爆炸荷载作用下，炮孔周围产生较大的环向拉应力，炮孔周围裂隙区主要是受拉破坏的结果，由爆炸荷载q1随距离的衰减公式为[24]

(22)

r1为粉碎区半径，取r1=3～5r0，r2为裂隙区半径，r2=10～15r0可以计算得10倍炮孔半径处爆炸荷载衰减为109.63 MPa，由此可知，爆炸应力波经过裂隙区较大幅度的衰减，地应力将对环向拉应力产生一定程度的影响，尤其在埋深-1 020 m时，实测地应力水平为35 MPa，为衰减后荷载的1/3，对其环向拉应力影响更为明显。故在炮孔远区，由爆炸荷载产生的环向拉应力随地应力(埋深)增加逐渐降低，而在炮孔近区，爆炸荷载将会产生较大的径向压应力，受地应力影响较小。

为验证上述分析，进行单孔直径80 mm爆破数值模型验证，其模型示意图如图12，模型边界施加不同地应力水平。由于理论模型无法反映剪应力随地应力变化的趋势，故数值模拟计算时，对压拉剪三者进行分析，弥补理论部分的缺少。取距炮孔中心d分别为0.2 m，0.5 m，1 m(5r，10r，25r，r为炮孔半径)处单元压应力、剪应力和拉应力水平，如图13。

图12 单孔计算模型Fig.12 The calculation model of single hole

在炮孔近区，即0.2 m(d=5r)处，拉应力保持较低应力水平，压应力与剪应力随着地应力水平增加而增加，且保持数百兆帕应力水平，较大的压剪应力使近处岩体产生压剪破坏，即炮孔近区主要受压应力和剪应力联合控制；在距炮孔0.5 m(d=10r)和1 m(d=25r)处，压剪应力随地应力的增加无明显变化，较炮孔近区的压剪应力峰值低1个数量级，而拉应力随地应力的增加而不断减小，使裂隙区(拉损伤区)范围减小。

(a) 压应力变化

为验证矿柱区域爆破损伤随地应力增加而减小的原因与是否与上述分析相符，取矿房矿柱交界面处的应力水平进行分析。由于炮孔底部预留0.7 m的垂直安全距离，扇形孔倾斜角度为40°～80°，即炮孔底部到矿房矿柱交界面的最小直线距离为1 m左右，炮孔半径为0.04 m，矿房矿柱交界面处距炮孔底部约为25倍炮孔半径，爆破损伤主要受拉应力控制，取矿房矿柱交界面处拉应力如下图14，可以看出，矿房矿柱交界面处拉应力大小随地应力的增加而减小，对比图10可知，损伤深度与拉应力呈正相关关系，与单孔爆破炮孔远区应力场变化相一致，即地应力的增加抑制拉应力的大小进而减小矿柱区域的爆破损伤深度。同样在图9中可以看出，矿房区域的爆破损伤(相邻扇形孔孔间的爆破损伤)随地应力增加无明显变化，可以间接证明在扇形孔近区主要受爆炸荷载产生的压剪应力作用，其压剪应力水平较高，受地应力的影响较小，导致只有矿柱区域(扇形孔远区)的损伤深度减小。

图14 矿房矿柱交界面处拉应力变化趋Fig.14 The variation of tensile stress at the interface between room and pillar

在胡英国[25]的研究中，通过最大拉应力准则、最大压应力准则和摩尔库伦准则对岩体爆破损伤特性进行分析，在2倍～10倍炮孔半径为压剪损伤区，其外围为拉损伤区，约占总体损伤的80%，由内而外，岩体爆破损伤类型由压剪损伤向拉损伤过渡；杨建华等[26]的研究中，认为爆炸荷载作用下，3.5倍炮孔半径范围内产生压剪损伤，而拉损伤的范围远大于压剪损伤，其损伤范围由岩体抗拉强度决定。本文的理论与数值模拟分析结果与上述两位学者的研究成果类似。

同时，胡英国[25]从时间尺度上，将岩石介质中的径向与环向应力进行组合，大致得到四个阶段的应力状态演化过程，如图15所示。I-径向压应力与环向压应力组合的压剪应力状态；II-径向压应力与环向拉应力组合的拉剪应力状态；III-径向拉应力与环向拉应力组合的拉剪应力状态，Ⅳ-径向拉应力与环向压应力应力组合的拉剪应力状态。炸药爆炸在孔壁岩体产生的压应力虽很大，但急剧衰减，应力状态I产生的损伤区域较小；若岩体在压剪状态I不能损伤，由于岩体的抗拉强度较小，极有可能会在阶段II、III、Ⅳ产生较大范围的拉损伤。

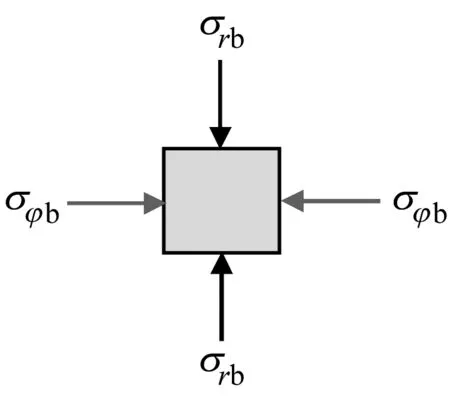
(a) 状态I

上述四种状态未考虑地应力的影响，若简单的将地应力水平考虑到上述作用过程中，由爆炸荷载诱发的环向拉应力与地应力符号相反，地应力的存在将会抑制II、III、Ⅳ状态的拉应力，若环向拉应力σφb在某一距离处衰减至与地应力同一水平，则此距离外的岩石所受拉应力将会降低至较低水平甚至不产生环向拉应力，岩石产生拉损伤的风险降低。

通过式(22)计算爆炸荷载在20倍炮孔半径处诱发的环向拉应力衰减33.29 MPa，30倍炮孔半径处诱发的环向拉应力衰减至17.17 MPa，根据不同埋深的地应力水平及拉应力的影响范围，可以估计，在地应力水平为19 MPa左右时(埋深-780 m)，可将矿房的安全距离设置为1.2 m，在地应力水平为35 MPa左右时(埋深-1 020 m)，可将矿房的安全距离设置为0.8 m，以此来减少扇形孔爆破开采过程中对矿柱造成的拉损伤深度，提高深部矿体开采过程中的安全性。

4 结 论

本文通过研究不同地应力水平下矿柱的损伤特性及地应力对爆破损伤区的作用机理，可以得出如下结论：

(1) 采场扇形孔爆破作用下，矿柱区域的爆破损伤主要受环向拉应力影响，随地应力增加，拉应力逐渐减小，矿柱损伤深度逐渐减小；在矿房区域，矿体破碎受多孔爆破产生联合作用，主要受压剪应力控制，地应力对矿房区域爆破损伤影响较小。

(2) 深部地应力的存在有利于减小扇形孔爆破损伤对矿柱的影响，随着地应力水平的增加，矿柱中部的爆破损伤深度衰减较慢，上部与下部区域的衰减趋势相同，在地应力水平大于20～30 MPa后矿柱爆破损伤将趋近相同深度，通过对拉应力影响范围的估计，建议-780 m和-1020 m埋深开采矿房时应保留的安全距离分别为1.2 m和0.8 m。

(3) 对比不同工况下矿柱的损伤深度可知，地应力水平为20 MPa左右时，矿柱的爆破损伤深度下降30%左右，地应力水平超过30 MPa后，矿柱损伤深度下降40%～50%左右，但地应力的增加无法消除爆破损伤的存在，深部地应力水平对矿体爆破开挖造成的影响不可忽视。

本文计算过程中，由于扇形孔孔身长，装药量大，在不同地应力水平下矿房的损伤形态基本相同，此时并未影响相邻炮孔间矿石的损伤效果，建议在不同埋深开采矿房时调整相邻扇形孔之间的角度，以控制扇形孔数量，达到相同的开采效果，节约钻孔的经济效益。