基于颗粒离散元的矿柱群连锁失稳机理分析

2018-09-20周子龙柯昌涛王亦凡

中国地质灾害与防治学报 2018年4期

周子龙，柯昌涛，王亦凡，周静

(中南大学资源与安全工程学院，湖南长沙 410083)

0 引言

房柱采矿法长期以来作为地下采矿的主要方法，矿石采出后在地下产生了大量空区，这些空区依靠矿柱群支撑顶板以上的岩体载荷，一旦矿柱群失稳，就会造成顶板大规模坍塌的地质灾害，甚至还会形成矿难。实际上，由于受地下水、腐蚀性化学物质以及物理风化等持续的侵蚀，矿柱的功能在不断退化，强度在持续减弱，最终会使矿柱群处于濒临崩塌的临界状态，一个微小的扰动就会诱发大规模失稳。国内外已经发生了很多矿柱群大规模失稳的灾害，造成了重大的人员伤亡、严重的设备损毁以及生产被迫中断的灾难性后果[1-5]。最典型的是1960年发生在南非的矿柱群大规模失稳的事故，近2 km2的空区坍塌，437个矿工被灾难夺去生命。一系列类似的灾难，引发了国内外学术界和工程界对矿柱群大规模失稳机理的研究和探讨，例如：ZIPF R K[1]对发生过矿柱连锁失稳的大量案例进行分析后发现，这些矿山在矿柱宽高比、开挖率、边界矿柱等方面具有相似的特征，即煤矿宽高比普遍小于3.0，金属非金属矿山普遍小于1.0，开挖率普遍高于60%，并且没有边界矿柱的存在。除了宽高比、开挖率、边界矿柱，BE′RESTA P[2]提出顶板的刚度对矿柱群失稳有一定的影响。POULSEN B A[6]对矿柱失稳过程中的载荷转移规律进行了定量的假设，并用数学方法对矿柱群连锁失稳的风险进行了定量的评估，引入概率方法预测矿柱群连锁失稳的概率；丘帆等[7]用Voronoi图的方法估算矿柱承担的顶板载荷面积，从而估算矿柱应力和评价系统稳定性；MA Haitao等[8]研究了采空区大规模坍塌的多米诺效应；周子龙等[9]应用重整化群理论计算矿柱群的临界失稳概率，并且开展了双矿柱的力学实验和数值模拟研究，揭示了双矿柱协同变形和强度特征[10-11]；REED GUY[12]提出了煤矿矿柱群和顶板的系统稳定性标准；LI Chong等[13]则尝试从矿柱群系统能量的角度出发解释多米诺失稳的机理。目前国内外的研究集中于矿柱大规模失稳的评价与案例分析，而对矿柱群失稳的动态过程和发生机制则研究的较少。因此本文利用PFC2D颗粒离散元软件建立了矿柱群数值模型，模拟矿柱群的渐进式失稳过程，揭示矿柱群连锁失稳的诱导因素和发生机制，具有实际意义和工程应用价值。

1 数值模型

某矿采用房柱法开采，形成了面积达1.2×104m2的采空区。空区埋深为h=500 m，地表地势平坦，围岩密度为ρ=3 169 kg/m3，垂直地应力可估算为σy=ρgh=15.5 MPa(g=9.8 m/s2)，由于空区埋深大，水平地应力不可忽视，水平地应力可根据侧压系数估算为σx=kσy=17.05 MPa，式中k为侧压系数取1.1。矿柱宽W=6 m，高H=6 m，矿房宽L=9 m，开挖率为e=84%。根据以上数据建立PFC2D数值计算模型见图1。模型长160 m，高56 m，顶板距离模型上边界30 m，底板距离模型下边界20 m，施加恒定的水平和垂直应力边界。

图1 PFC2D多矿柱数值模型及恒定应力边界Fig.1 Numerical model of multiple pillars with PFC2D and its constant stress boundary condition

1.1 黏结模型及微观参数

PFC中最基本的单元是球(三维)或单位厚度的圆盘(二维)，称为颗粒，通过给颗粒赋予微观物理力学参数，来模拟材料的宏观力学行为。通过在颗粒的接触处施加黏结模型将颗粒散体黏结为一个具有强度的宏观物体，PFC中存在两种黏结模型，接触黏结和平行黏结。接触黏结模型作用于颗粒接触点处，等效于在颗粒的接触点处用胶水黏结，在黏结点处只能承受力而无法承受力矩的作用。平行黏结模型是更接近材料微观黏结本质的模型，图2所示是平行黏结模型和颗粒接触的示意图，表1列出了颗粒和平行黏结微观参数。

图2 PFC2D颗粒接触及平行黏结模型示意图Fig.2 Schematic of particle and parallel bond in PFC2D

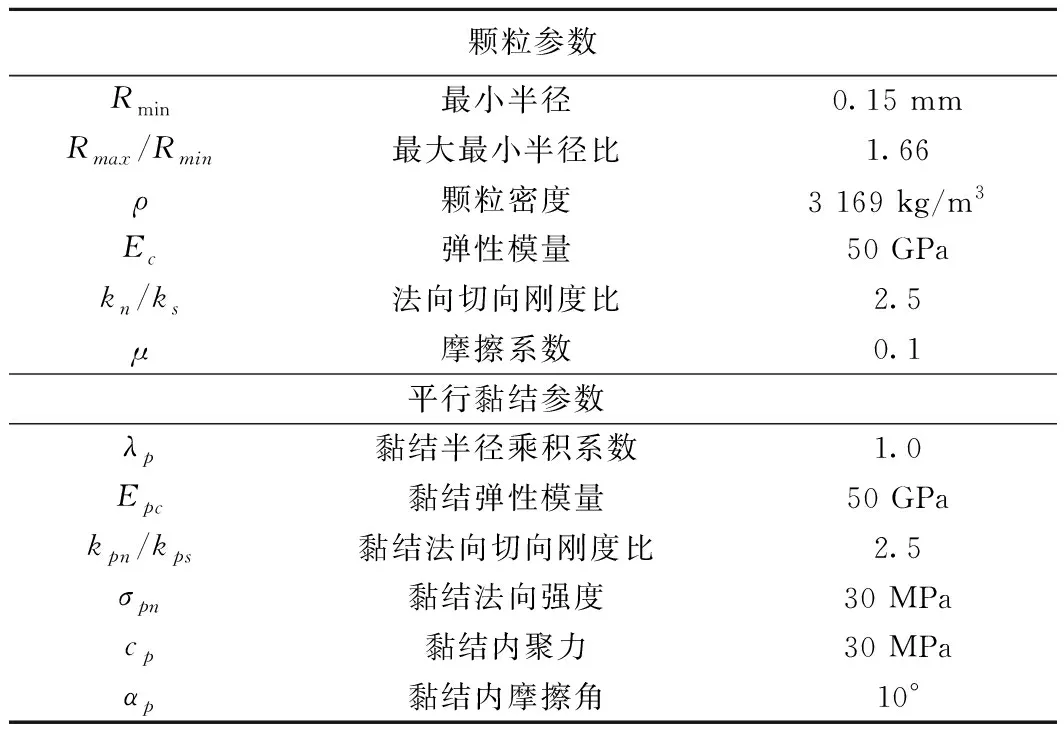
颗粒参数Rmin最小半径0.15 mmRmax/Rmin最大最小半径比1.66ρ颗粒密度3 169 kg/m3Ec弹性模量50 GPakn/ks法向切向刚度比2.5μ摩擦系数0.1平行黏结参数λp黏结半径乘积系数1.0Epc黏结弹性模量50 GPakpn/kps黏结法向切向刚度比2.5σpn黏结法向强度30 MPacp黏结内聚力30 MPaαp黏结内摩擦角10°

平行黏结模型等效于一个充填在两个颗粒之间的胶结体，能够承受力和力矩的作用。在PFC2D中，平行黏结等效于一个单位厚度的长方体，其三个维度的尺寸为：

Rp=λpmin(RA,RB)

Lp=(RA+RB)/2t=1

(1)

颗粒在运动过程中，平行黏结内部产生应力，当黏结体内部应力超过强度极限时，平行黏结破裂，当微观裂纹贯通时可以模拟宏观破裂。给模型安装平行黏结，在现场取得50 mm×100 mm长方体岩石取样，测得单轴压缩应力应变曲线，用于校正数值模型微观参数。在PFC2D中建立与岩石试样相同尺寸的数值模型，通过不断调整微观力学参数，使得模拟得到的单轴压缩应力应变曲线与实验获得的曲线较好地吻合，对应的微观力学参数值列于表1。

1.2 计算步骤

模型计算步骤如下：(1)建立模型，施加微观力学参数，计算使得颗粒达到平衡状态；(2)在模型顶部施加垂直应力σy=15.5 MPa，计算后达到平衡；(3)通过伺服机制移动垂直墙体使模型达到水平应力σx=17.05 MPa；(4)给模型施加平行黏结，开挖矿房颗粒，在1#到7#矿柱中建立应力监测圆监测矿柱应力，计算达到平衡状态；(5)删除4#矿柱，测得1#～3#和5#～7#矿柱垂直应力曲线。

2 结果分析与讨论

2.1 矿柱群连锁失稳过程分析

图3(a)是4#矿柱失稳后，1#～7#矿柱垂直应力的变化情况，图3(b)是各矿柱应力峰值时刻的裂纹发展情况，在A～F的各个时刻各矿柱的垂直应力列于表2。在A时刻，各矿柱都处于稳定状态，此时1#～7#矿柱垂直应力分别为37 MPa、38 MPa、39 MPa、41 MPa、39 MPa、38 MPa、37 MPa，矿柱中无裂纹出现。

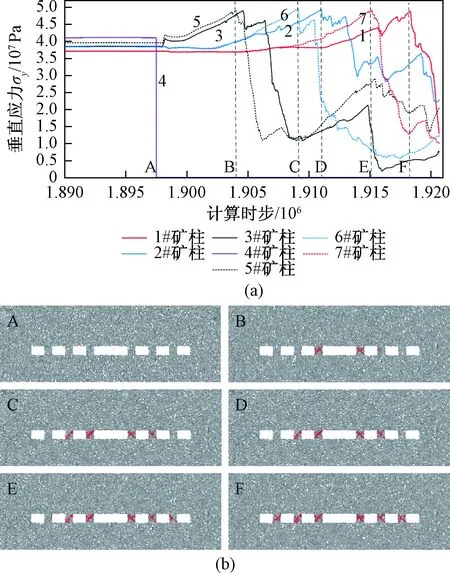
图3 矿柱应力变化及裂纹扩展Fig.3 Vertical stress variation and crack growth of the pillars

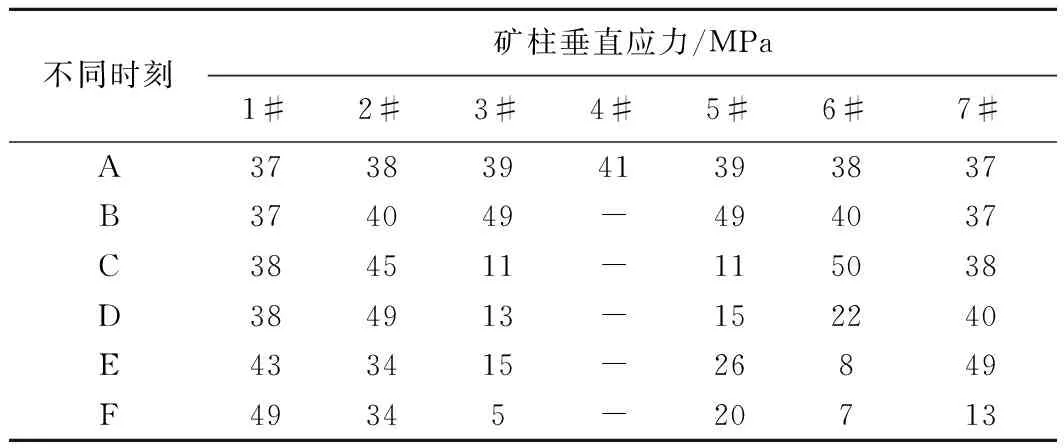
不同时刻矿柱垂直应力/MPa1#2#3#4#5#6#7#A37383941393837B374049-494037C384511-115038D384913-152240E433415-26849F49345-20713

4#矿柱失稳(删除颗粒单元)后，3#和5#矿柱最先受到影响，应力开始增加，3#矿柱和5#矿柱的应力增加速度大致相等，在B时刻均达到强度峰值，分别为49 MPa、49 MPa，3#矿柱呈东北向西南的45°剪切破坏，5#矿柱呈西北到东南的45°剪切破坏。在3#和5#矿柱应力增加过程中，1#、7#、2#、6#矿柱应力基本保持不变，3#和5#矿柱应力接近峰值的时候，2#和6#矿柱应力开始增加，6#矿柱在C时刻达到应力峰值50 MPa，矿柱呈西北到东南的45°剪切破坏。随后在D时刻，2#矿柱达到强度峰值49 MPa，矿柱呈东北向西南的45°剪切破坏。6#矿柱达到峰值破坏时，1#和7#矿柱应力开始增加，7#矿柱在E时刻达到应力峰值49 MPa，矿柱呈西北到东南的45°剪切破坏。到F时刻，1#矿柱应力达到峰值49 MPa，矿柱呈东北向西南的45°剪切破坏，至此全部矿柱发生破坏。

根据应力曲线峰值，1#～3#，5#～7#矿柱的强度分别为49 MPa、49 MPa、49 MPa、49 MPa、50 MPa、49 MPa，根据计算公式：安全系数=矿柱强度/矿柱应力，矿柱群处于稳定状态即图中A时刻的安全系数分别为：1.32、1.29、1.26、1.26、1.32、1.32。在A时刻时，矿柱的剩余强度只有10 MPa，4#矿柱失稳后，转移到各个矿柱上的应力使它们的载荷上升达到强度值，安全系数下降到1.0，造成邻近矿柱的连锁失稳。另外，矿柱在破坏过程中的裂纹发生发展有一些共同的特点：5#、6#、7#矿柱的剪切裂纹都是从西北往东南的45°方向，而1#、2#、3#矿柱的剪切裂纹却是从东北往西南的45°方向，这可能是由于顶板的沉降使矿柱受到弯矩的作用导致，1#、2#、3#矿柱的弯矩方向与5#、6#、7#矿柱弯矩方向相反。

2.2 不同的矿柱安全系数诱发连锁失稳结果分析

根据2.1节的分析，矿柱的初始安全系数分布在1.26～1.32，通过移除空区中间位置的矿柱，随即诱发了连锁失稳。在本节通过提高平行黏结模型的微观强度参数，增强矿柱的强度，保持其它一切变形参数不变，然后移除4#矿柱，观察矿柱是否发生大规模失稳。开展了两组数值模拟研究，微观参数的取值见表3。

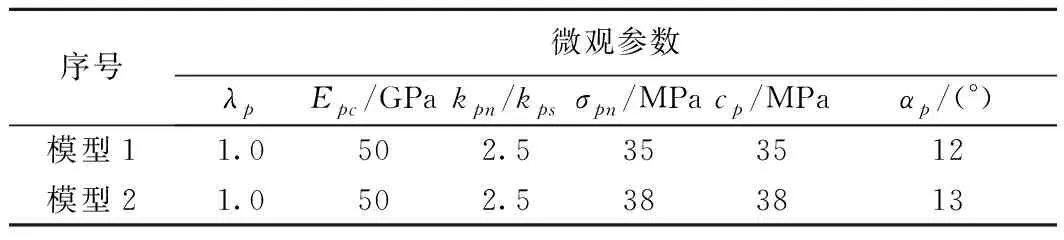
表3 不同安全系数的平行黏结微观参数

模型1的矿柱应力变化曲线见图4(a)，矿柱破坏裂纹扩展见图4(b)，在不同时刻各矿柱垂直应力值列于表4。

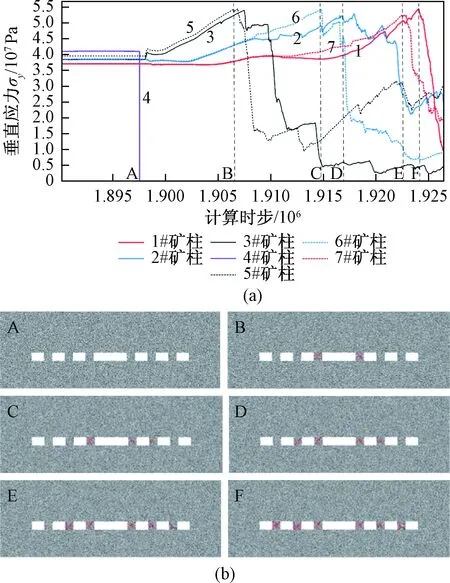
图4 矿柱应力变化及裂纹扩展Fig.4 Vertical stress variation and crack growth of pillars

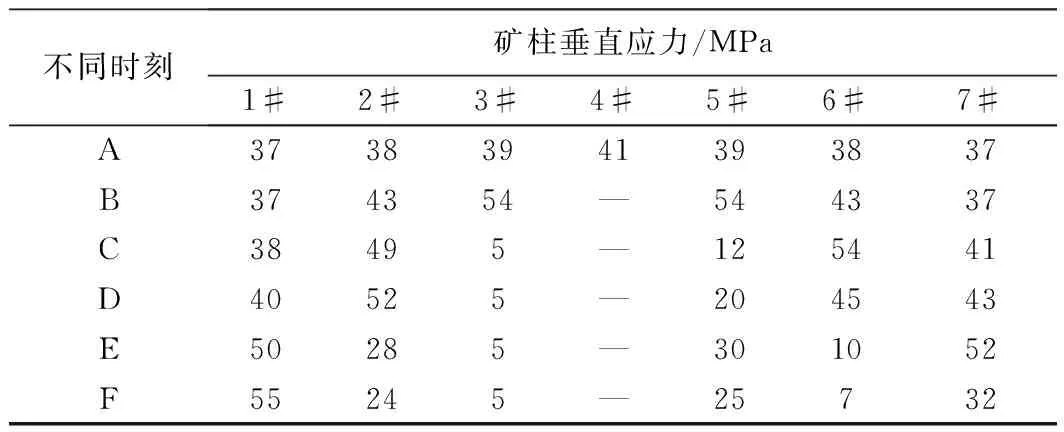
不同时刻矿柱垂直应力/MPa1#2#3#4#5#6#7#A37383941393837B374354—544337C38495—125441D40525—204543E50285—301052F55245—25732

图4(b)矿柱的破坏顺序与图3(b)一样，图4(a)的应力变化曲线与图3(a)也十分相似。在A时刻的稳定状态时，1#～7#矿柱的垂直应力分别为37 MPa、38 MPa、39 MPa、41 MPa、39 MPa、38 MPa、37 MPa。删除4#矿柱后，在B时刻，3#和5#矿柱应力达到峰值54 MPa，3#和5#矿柱破坏后，2#和6#矿柱应力开始大幅增加，分别在D时刻和C时刻达到峰值52 MPa、54 MPa，2#和6#矿柱破坏后，1#和7#矿柱应力开始增加，分别在F时刻，E时刻达到峰值强度55 MPa、52 MPa。根据应力曲线峰值，1#～3#，5#～7#矿柱的强度分别55 MPa、52 MPa、54 MPa、54 MPa、54 MPa、52 MPa，计算得到矿柱的初始安全系数分别为：1.49、1.37、1.38、1.38、1.42、1.41，安全系数分布在1.37～1.49。模型1的结果与图3相比，微观参数增大后，矿柱强度提高，矿柱安全系数也相应提高，因此矿柱能够承载更多的转移载荷，模型1中矿柱承载的转移载荷增大为18 MPa，相比图3的10 MPa有所提高，但是矿柱仍然发生了大规模的连锁失稳，可知此模型的载荷转移量大于18 MPa，要想避免连锁失稳，必须进一步提高矿柱安全系数值。

模型2相对模型1具有更高的矿柱强度，其它所有参数保持一致。得到的应力变化曲线见图5。

图5 矿柱应力变化曲线Fig.5 Vertical stress variation of pillars

由图5可知，4#矿柱失稳后，3#和5#矿柱的应力分别增加到54 MPa和55 MPa后达到稳定的状态，2#和6#矿柱最终应力增加到44 MPa后达到稳定状态，1#和7#矿柱应力基本保持不变，矿柱群的连锁失稳没有发生。由此推断，在图1所示的矿柱和顶板结构形状和地应力状态以及表1所示的岩石变形微观力学参数条件下，矿柱群发生连锁失稳的临界安全系数就位于模型1和模型2之间。

2.3 不同的矿柱破坏位置诱发连锁失稳结果分析

2.1节和2.2节模拟了采空区中央位置的矿柱失稳诱发连锁失稳的情况，以及诱发连锁失稳的矿柱安全系数临界条件。通常，由于采空区顶板的沉降，中央位置的顶板沉降最大，使整个空区顶板呈现出一个类似漏斗的形状，由此造成空区中央位置的矿柱应力最大，越靠近空区边缘，矿柱应力越小，空区中央位置的矿柱失稳带来的扰动效应一般来说也最严重。实际工程中的采空区矿柱形状往往不规则，矿柱布局也不均匀，矿柱应力大小不一，因此不一定是空区中央的矿柱最先失稳，本节将探讨空区边缘的矿柱失稳是否会诱发矿柱连锁失稳的问题。基于图1所示的数值模型和表1的颗粒微观力学参数，模型达到平衡状态时，移除边缘的1#矿柱，得到的应力变化曲线如图6所示。

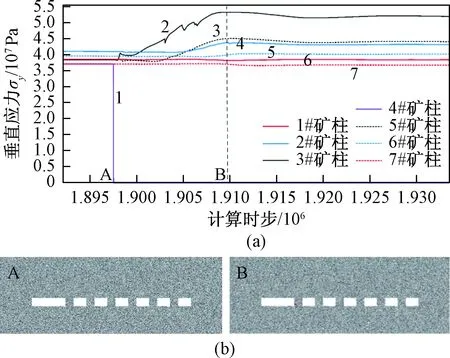
图6 边界矿柱失稳后应力变化曲线Fig.6 Vertical stress variation and crack growth of pillar 2#～6# after pillar 1# fails

A时刻矿柱处于稳定状态，1#～7#矿柱的垂直应力分别为37 MPa、38 MPa、39 MPa、41 MPa、39 MPa、38 MPa、37 MPa，根据2.1的分析，矿柱初始安全系数分别为：1.29、1.26、1.26、1.26、1.32、1.32。1#矿柱移除后，2#矿柱的应力上升后又小幅下降最终稳定在52 MPa，最终安全系数下降到0.94。2#矿柱安全系数小于1.0，但是图6(b)B时刻的裂纹图表明2#矿柱中并没有形成贯通的裂纹，2#矿柱并没有发生破坏，可能是因为两个方面的原因：一是矿柱内应力分布不均匀，局部应力很高，造成了矿柱的局部破坏，如图6(b)，2#矿柱左下角和右上角有少量裂纹扩展，但并没有贯通；二是边界矿柱对顶板的端部支撑作用，此时顶板类似悬臂梁，沉降得到有效控制，没有对2#矿柱形成持续的加载，图6(a)也证明2#矿柱的应力最终维持平稳状态，因此没有造成2#矿柱的破坏。与此不同的是，中央位置的矿柱失稳，由于离边界矿柱远，边界矿柱对顶板的沉降发挥不了有效的约束作用，顶板的沉降对矿柱形成了持续的加载，直到矿柱破坏。2#矿柱未失稳，发挥了类似边界矿柱的作用，因此3#～7#矿柱也保持稳定，3#矿柱应力最终增加到44 MPa后稳定，4#矿柱应力增加到43 MPa后稳定，而5#、6#、7#矿柱的应力基本不变，没有受到1#矿柱失稳的影响。

2.4 不同刚度对矿柱群连锁失稳的影响

在PFC2D中，颗粒法向刚度与弹性模量成正比，因此要研究刚度对矿柱群连锁失稳的影响，只需要改变颗粒弹性模量Ec的值就能实现不同的刚度。在图1数值模型和表1微观力学参数的基础上，分别将弹性模量缩小10倍和增大10倍，不改变法向刚度切向刚度的比值，其它参数也保持不变如表5所示，分别建立两组模型，按1.2节的步骤开展计算。

表5 不同顶板颗粒刚度参数

在模型1的软弱顶板条件下，得到的矿柱应力变化曲线见图7，各峰值时刻各矿柱的垂直应力值见表6。

图7 矿柱应力变化曲线Fig.7 Vertical stress variation of pillar 1#～7# after 4# fails

所得的图7矿柱破坏的顺序与图3基本一致，呈现出渐进的破坏顺序，4#矿柱失稳瞬间，5#和3#矿柱首先在B时刻破坏，6#和2#矿柱分别在C时刻和D时刻破坏，最后破坏的是位于空区两边的1#和7#矿柱，破坏顺序呈现出典型的“多米诺骨牌效应”。由表6可知，1#～3#、5#～7#矿柱的强度分别45 MPa、50 MPa、49 MPa、49 MPa、49 MPa、50 MPa。

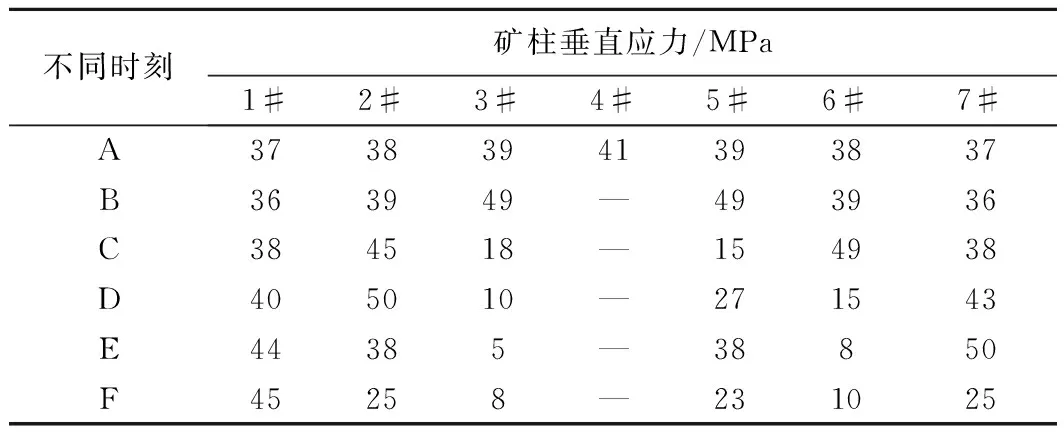
表6 软弱顶板条件下矿柱垂直应力变化值

模型2的坚硬顶板条件下所得的计算结果如图8所示。各时刻矿柱垂直应力值见表7。

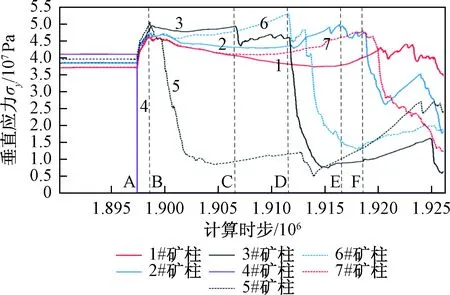
图8 矿柱应力变化曲线Fig.8 Vertical stress variation of pillar 1#～7# after 4# fails

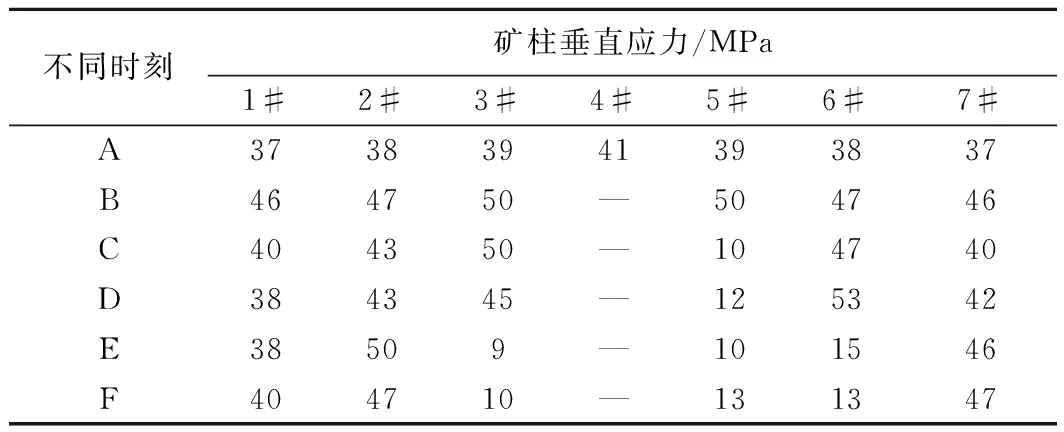
不同时刻矿柱垂直应力/MPa1#2#3#4#5#6#7#A37383941393837B464750—504746C404350—104740D384345—125342E38509—101546F404710—131347

由图8可知，在坚硬顶板条件下，所得和结果与软弱顶板条件完全不同，图8的应力曲线变化方式与图7有本质的区别。在删除4#矿柱的瞬间，即A时刻，1#～3#、5#～7#矿柱的应力都明显增加，在B时刻同时达到峰值，3#和5#矿柱应力增加了11 MPa，2#和6#矿柱应力增加了9 MPa，1#和7#矿柱应力也增加了11 MPa，说明在顶板刚度非常大的情况下，4#矿柱的失稳瞬间使得顶板的载荷均匀地转移给剩余的矿柱。B时刻之后，1#～3#、5#～7#矿柱的应力几乎不再增长，5#矿柱率先失稳，应力迅速下降，1#和3#矿柱的应力经过一段平稳的时期也开始迅速下降，2#、6#、7#矿柱应力有微小的增加后也迅速破坏，因此总结图8中各矿柱的破坏特征，可以发现矿柱群失稳的顺序不再具有图7渐近式失稳的特征，因此在坚硬顶板条件下矿柱群失稳不再显著地表现出“多米诺骨牌效应”。由此可以证明，顶板刚度在矿柱群大规模失稳中确实发挥了重要的作用，这种作用主要体现在影响载荷转移上，当顶板较软弱时，矿柱的载荷转移从失稳诱发矿柱开始，离失稳诱发矿柱越远，受到载荷转移的影响就越迟；但是当顶板是刚度很大的硬岩时，在失稳瞬间，载荷几乎同时均匀地转移到剩余稳定的矿柱中。值得一提的是，PFC模拟岩石材料时的微观颗粒弹性模量不可能达到500 GPa之大，因此在矿柱群失稳过程中，载荷均匀转移到所有矿柱上的情况较少，图7的矿柱应力转移模式是最常见的。