双索非线性振动瞬时相位差及其来源

孙测世，林俊强，邓正科

(1.重庆交通大学 土木工程学院，重庆 400074；2.湖南城市学院设计研究院有限公司，长沙 410005)

工程中索结构的振动危害极大，一直是人们关注的重点问题[1-3]。从相位来看，各索若处于同步振动状态(同相)，即拉索的惯性力方向一致时，拉索对锚固结构的作用力瞬间增大数倍，可造成锚固结构严重受损；若各索处在异步振动状态(异相)，则极易引起邻索间的碰撞[4-6]，导致索结构的使用寿命大大缩减。

目前，对多索结构的研究已表明，参数差异对相邻拉索的相对振动存在较大影响。孙测世[7]进行了斜拉桥全桥模型试验，发现当激励频率达到一定值时多根索会发生大幅振动，且相邻索的振动间均存在一定相位差，导致产生碰撞。孟新田[8]建立了斜拉桥的多索-梁动力学简化模型，分析了双索间在倍频关系下拉索的大幅振动问题。赵跃宇等[9]建立了一种双索质量块模型，分析了拉索与拉索之间在振动过程中的相互影响，研究发现单根拉索参数的变动对相邻拉索振动的影响较大。国内外学者对于拉索的相对振动的研究在模态分析中往往以“同相”与“反相”模态体现，Lepidi等[10]采用一个具有双索的简化模型研究了索承重桥梁的模态耦合，研究表明拉索存在同相和反相的局部模态。Ahmad等[11]建立了双索网络结构，研究了辅助索刚度对双索网络平面内自由振动特性的影响，发现双索网结构在平面内自由振动中存在同相和反相模态。Abdel-Ghaffar等[12]首次研究了拉索振动过程对斜拉桥振动产生的影响，研究表明MECS模态分析中可获得大量拉索局部模态，其中包括相邻拉索的同相和反相模态。吴庆雄等[13]对多索-梁结构的研究中发现二索-梁结中也存在同相和反相模态，并且在此基础上建立了多索梁模型。Zhou等[14]提出并分析了在锚索锚固附近布置有阻尼器的两根平行拉索系统，研究发现第三模态下两平行索之间振幅同相，第四模态下两平行拉索振幅反相。

对其他类似结构的研究中也表明相频特性随结构参数变化。最为典型的结构为摆，根据参数的差异，其相位角、相位差会有不同的影响和变化，会呈现同步或异步运动的现象[15-17]；Kapitaniak等[18]通过在平台上两个平面弹性摆加水平激励，发现了稳定的同异步运动状态，并分析了同异步振动下的分岔情形。

综上，索的相频特性与物理参数和激励密切相关，相邻拉索会因参数关系改变而出现同步或异步振动。本文对双水平索质量块模型展开对索的瞬时相位差研究，揭示不同参数下高阶近似项中引起双水平索非线性振动瞬时相位差的因素及其影响规律。

1 力学模型与多尺度分析

1.1 基本假定

如图1所示双水平索与质量块耦合振动力学模型，其中质量块M仅考虑沿索轴向的运动X(t)，不考虑质量块阻尼。其中，跨度为l，跨中垂度为d。索的单位长度质量m，以索的轴向方向为x方向，重力加速度g的方向为y方向。x、y方向对应位移分别用u、v表示。

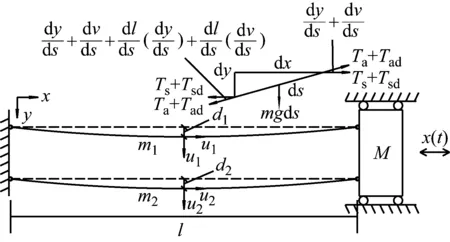
图1 双水平索与桥面耦合力学模型Fig.1 The coupling mechanical model of double horizontal cable and bridge deck

其它基本假设包括：①不考虑索和梁的材料非线性；②不计拉索的抗弯刚度、抗扭刚度以及抗剪刚度；③认为两根拉索的重力垂度均为抛物线；④拉索的本构关系服从胡克定律并且各点受力均匀；⑤不计桥塔振动对索的影响；⑥只考虑桥面的竖向运动。

1.2 振动方程的建立

根据Hamilton原理，拉索的动力学方程为

(1)

其中

式中：m为单位长度质量;E为拉索弹性模量;A为拉索截面面积;εd为拉索振动中的动应变。y(x)水平索的静态构型，其表达式可为：

y(x)=4f(1-x)x

(2)

式中，f为悬索垂跨比。

当引入质量块位移函数X(t)和阻尼项后可得到

(3)

引入如式(4)中的无量纲变换

(4)

(5)

类似地，将质量块的运动方程进行无量纲化后可得

(6)

1.3 离散化模型

悬索的振动可以表示为各阶模态振动的组合，因此可利用分离变量法令

(7)

(8)

式中:v1(x,t)、v2(x,t)分别表示索1和索2的动位移；qn(t)、Bn(t)为索1和索2振动的广义时间坐标；Φ(x)为索1和索2振型函数，其正对称模态函数Φ1(x)和反对称模态函数Φ2(x)如下[19]

(9a)

(9b)

利用Galerkin方法进行离散，可将包含时间二阶项和空间二阶项无量纲偏微分方程简化为只含有时二阶项的无量纲离散控制方程，将相应的量代入，联合各式并简化系数，则可得相应双水平索质量块耦合振动方程组如下

(10a)

(10b)

(10c)

式中，各系数如下：

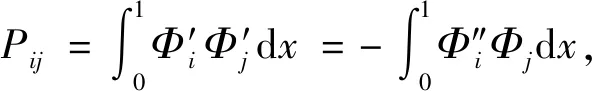
1.4 摄动分析

基于多尺度法对式(10a)～(10c)求近似解，令：

q(t;ε)=εq0(T0,T1,T2)+ε2q1(T0,T1,T2)+

ε3q2(T0,T1,T2)+…,

(11a)

B(t;ε)=εB0(T0,T1,T2)+ε2B1(T0,T1,T2)+

ε3B2(T0,T1,T2)+…,

(11b)

Z(t;ε)=εZ0(T0,T1,T2)+ε2Z1(T0,T1,T2)+

ε3Z2(T0,T1,T2)+…,

(11c)

其中，Tn=εnt(n=0,1,2,3,…)，代入式(10a)～(10c)并按ε的幂次整理得到：

ε：

(12a)

(12b)

(12c)

ε2：

(13a)

(13b)

(13c)

ε3：

(14c)

设式(12a)～(12c)的复数解为

qk1=A1eiω1T0+cc

(15a)

Bk1=A2eiω2T0+cc

(15b)

Z1=A3eiω3T0+cc

(15c)

代入式(13a)～(13c)，令长期项为0，可得特解：

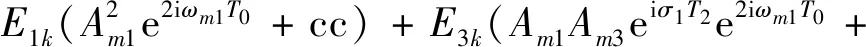
(16a)

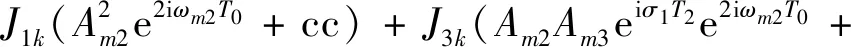
(16b)

(16c)

式中，各系数如下：

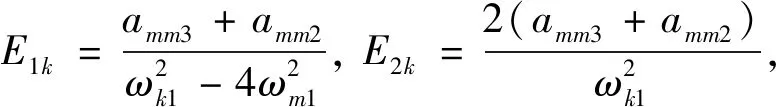
再将式(15a)～(16c)代入式(14a)～(14c)取双索和质量块三阶长期项为0可得：

其中：

Tem=-am1F4k-am1F3k-3am4+

为便于求解式(17a)～(17c)，假定质量块仅提供拉索轴向激励X(t)=QcosΩt，其中Q为质量块的无量纲振动幅值，为质量块的实际激励幅值Qb除以索长l，即：Q=Qb/l。令Amn=1/2aneiβn(n=1,2)，代入式(17)，并设稳态振动时

经分离实、虚部可得平均方程

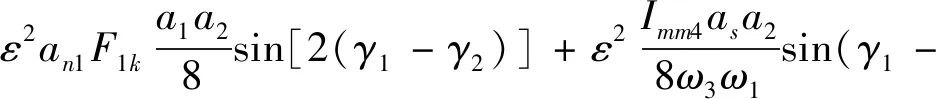
(18a)

(18c)

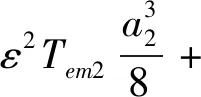
(18d)

由式(18)可知，至此问题转化为四个方程求解a1、a2、γ1和γ2四个未知数的非线性代数方程组，虽然一般可以通过直接简化方程，研究非平凡稳态解的稳定性，但是由于简化过程存在耦合项，直接求解比较困难，因此引入直角坐标的方法，做以下转换

sinγ1=p1m/a1，cosγ1=q1m/a1

sinγ2=p1n/a2，cosγ2=q1n/a2

再利用数值计算方法求解方程组，最后得双索响应近似解为

2 不同计算方法的对比验证

为验证基于多尺度法的计算结果的正确性，本节利用算例将数值结果与Runge-Kutta法直接积分、有限元法计算结果进行对比。在给定参数m1=m2=136 kg/m、l=440 m、EA=2.98×109N、H1=8 000 kN、Q=0.000 1等基础上，改变另一根拉索的索力参数。为结果具有一般性，选用垂跨比这一在工程中较常用和直观的无量纲参数进行分析。按f1=0.009，f2=0.011或0.01，考虑两个不同垂跨比之比的工况，即f2/f1=0.01/0.009=1.11和f2/f1=0.011/0.009=1.22。

利用有限元软件ANSYS建立双索质量块模型，采用LINK10模拟拉索单元。质量块采用MPC184单元模拟，不考虑阻尼力与弹性恢复力，仅作为一个连接两根拉索的物体，具有无穷大的刚度和一定的质量，通过给质量块一个x方向的动位移，使双索产生参数振动。同时，采用四阶Runge-Kutta编制MATLAB程序直接对常微分方程式(10)进行直接数值积分。

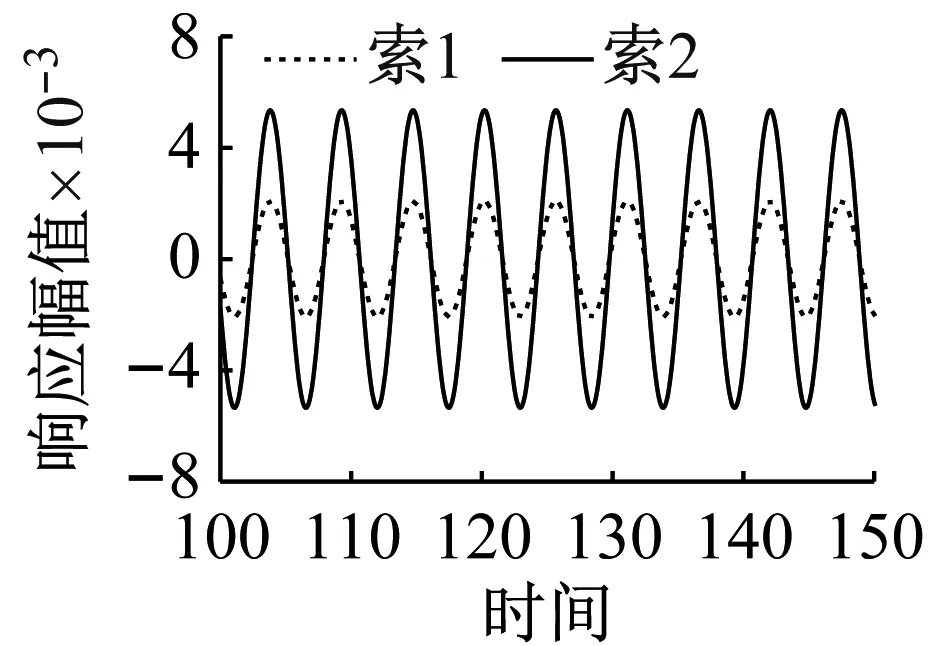
下文将以f2/f1=1.11和1.22，Ω=1.05作为算例进行分析，模拟两组参数下的相对振动，绘制出相应的时程曲线图与Runge-Kutta法求得的响应以及非线性有限元分析结果进行对比。为方便比较，将有限元的有量纲的数据转化为无量纲，对比结果如图2和图3所示。可见，在参数条件为f2/f1=1.11，Ω=1.05时，索1与索2处于同步振动；在参数条件为f2/f1=1.22，Ω=1.05时，索1和索2处于异步振动。

比较两组不同拉索参数下的Runge-Kutta法与多尺度法所得的时程曲线，可见两组不同参数下两种求解方法的结果吻合良好。有限元分析得到的时程曲线的上波峰到下波峰的距离均有微小的减小，但二倍频项与漂移项的影响确有微小增大。这是由于进行理论分析与Runge-Kutta法计算时，均忽略了面内外耦合。在进行非线性有限元分析时，给与了面外微小扰动，振动过程面内外有一定的耦合，分散了系统的振动能量，因此振动幅值会有所减小。综上可见，无论是Runge-Kutta法还是非线性有限元分析，结果都与多尺度法结果有较好的吻合，验证了多尺度方法求解结果的可靠性。

(a) 多尺度法与R-K法结果对比

3 高阶解对相频特性的影响

为研究高阶解对相频特性的影响，继续通过第2章算例分别考察高阶近似项中的相移值γ1和γ2、漂移项等因素对瞬时相频特性的影响，进一步阐述不同参数下双水平索的相对振动变化规律。

3.1 高阶近似项对瞬时相位的影响

图4为f2/f1=1.11，Ω=1.15时的时程曲线。其中，图4(a)为仅考虑线性近似解双索响应时程曲线，图4(b)为考虑ε的前两阶时双索的时程曲线图。横坐标为无量纲时间变量，纵坐标为无量纲响应幅值。

(a) 未考虑高阶近似项

对比图4(a)、图4(b)可知，未考虑高阶近似项时，两根索在振动过程中瞬时相位差值变化波动不大，且索1受高阶项的影响相对较小；在考虑高阶近似项时，受到高阶近似项中二倍频项及漂移项的影响，响应曲线线型会产生较大的变化。故可推断出两根拉索在相移值为零(γ=0)时，两根拉索会产生一定的瞬时相位差异，因此，绘制了双索在f2/f1=1.11时的复平面图。

如图5所示，在未考虑高阶近似项时，两根拉索的复平面图都为圆形，相同时刻对应点均在外圆的半径上，相角差值为零。当考虑高阶近似项时，索1与索2的复平面图中心点均产生一定的偏移，索2尤为明显，从而使复平面图中对应曲线形状发生变化。两根拉索的瞬时相位差也会因为高阶项的存在出现差异，如图6所示。为了便于比较，定义无量纲参数为

(20)

式中，Δp为两根拉索间响应的瞬时相位差。

(a) 未考虑高阶近似项

在未考虑高阶近似项时，即在相移值γ1和γ2为零时，其瞬时相位差幅值也为零，如图6中虚线所示。当考虑高阶近似项时，受到高阶近似项的影响，瞬时相位差会呈现很大的变化幅度，相位差时程曲线成周期变化，在该参数条件下，最大相位差可达到0.2π，如图6中实线所示。

为更加直观的分析在不同参数下的瞬时相位差变化情况，定义新的无量纲参数

(21)

式中，Δpmax为Δp的幅值。

取各频率下两根拉索间响应的瞬时相位差幅值pmax，绘制pmax-Ω曲线图，将考虑高阶近似解与仅考虑线性近似解时瞬时相位差随频率变化曲线图进行对比，如图7所示。

由图7可知，当Ω<1.05时，双索处于同步或异步振动(图7(a)中为异步振动，图7(b)中为同步振动)，两根曲线几乎重合，说明高阶近似项对双索间的瞬时相位差无明显影响；当Ω>1.05时，相位差逐渐变大；当Ω>1.10后，差异明显增大，此时高阶近似项对相位差的影响不可忽略。图7(b)中，在特定频率下，高阶近似项甚至能使瞬时相位增大0.8π。

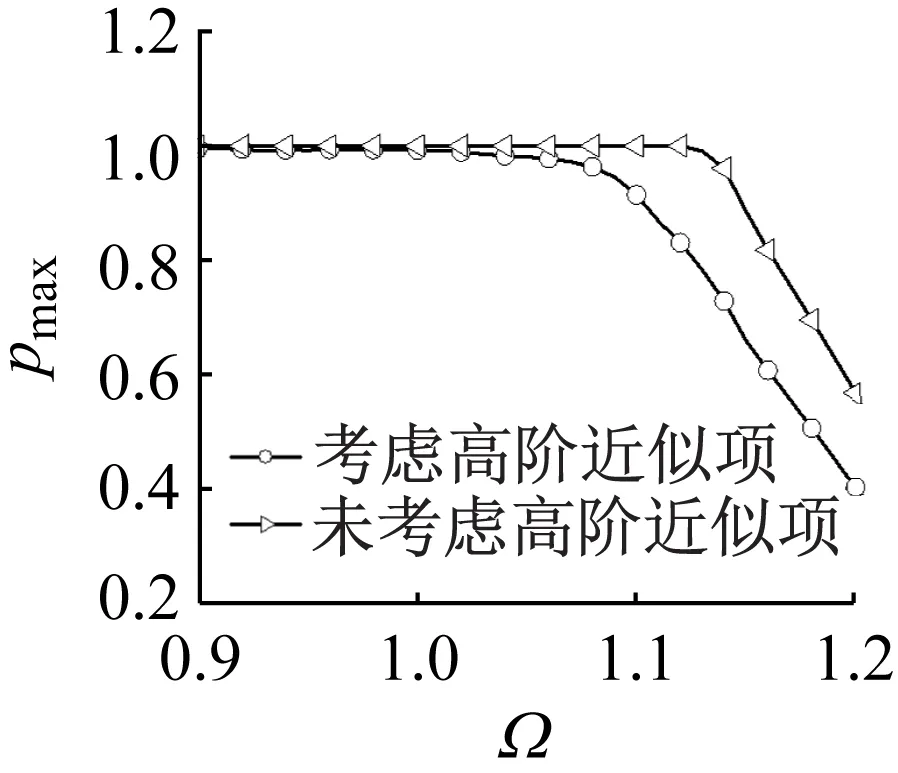
(a) f2/f1=1.22

综上所述，考虑高阶近似项后，拉索间的瞬时相位差会有很大的变化，因此，在对索的相频特性分析时，不能忽略高阶近似项的影响。

3.2 高阶近似项中各因素对瞬时相位的影响

在3.1节基础上，为进一步追溯高阶近似项中导致其“不能忽略”的因素。将第2章已经验证的MATLAB程序进行适当修改，使高阶项中的相移值γ以及漂移项的影响剥离出来进行分析。

3.2.1 相移值γ对瞬时相位的影响

由式(19a)、(19b)可知，在双索的近似解中，无论是漂移项还是二倍频率项均含有相移值γ，可见相移值γ的存在可能对响应会有一定的影响，因此绘制出f2/f1=1.11，Ω=1.15时的瞬时相位时程曲线图与瞬时相位差曲线图，如图8所示，两者进行比较，研究相移值γ对相频特性的影响。

由图8(a)可知，瞬时相位差时程曲线不仅向右平移而且向下平移。向右平移是因为两根拉索的相移值γ不为零，响应时程与瞬时相位时程均产生一定的右移。而因为两根索相移值存在一定的差异，从而导致瞬时相位差值整体加上或减去一个定值，所以瞬时相位差时程曲线会产生一定的下移。故图8(a)中Δt和Δ(Δp)的数值大小取决于两根拉索在同一频率下的相移值大小(Δt为瞬时相位差时程曲线幅值往右偏移的时间差，Δ(Δp)为瞬时相位差时程曲线幅值往下偏移的瞬时相位差的差值)。

(a) γ=0和γ≠0的瞬时相位差

考虑了相移值后，如图8(b)所示，瞬时相位差时程曲线会向右平移，两曲线在同一时刻上对应两点的相位差数值大小就是相移值γ。双索结构由于两根拉索的参数差异，相移值也可能会具有较大差异，而且瞬时相位时程曲线线型也具有一定的差异，故瞬时相位差也会受到较大的影响。

对于双索近似解，如式(19a)、(19b)中含有二倍频项与漂移项，分别绘制出γ=0和γ≠0时各项系数的变化曲线，如图9所示。

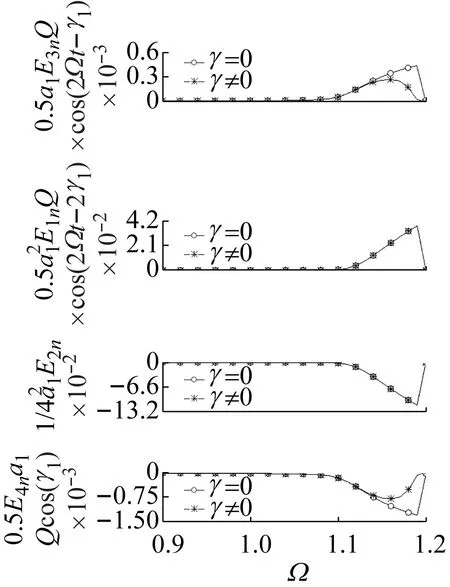
(a) f2=0.01

由图9可知，高阶近似项各项系数中均含有响应幅值a1、a2。在向上扫频时，由于响应幅值a1、a2增大，各项系数绝对值也相应的增大。将各项参数进行对比，可见仅第一项与第四项在γ=0和γ≠ 0时较大的激励频率Ω区域时出现明显差异。但第一项与第四项的数值大小相对于第二项与第三项为小量，数值上可以忽略不计。因此可知，γ对高阶项引起的相位差幅值的影响可以忽略。

3.2.2 漂移项对瞬时相位的影响

从式(19a)、(19b)中可见，响应幅值是漂移项中的参数，因此响应幅值对瞬时相位可能也有一定的影响。根据文献[20]表明，瞬时相位的变化与漂移项在响应振幅中所占比重有关。所以漂移项会影响瞬时相位数值变化，可通过漂移项在响应振幅中所占比重对瞬时相位差幅值进行定性研究。由图9可知，可将第一项和第四项的幅值忽略，令式(19a)、(19b)中二倍频率项的余弦值为1，振动达到振幅，则可定义新的无量纲参数

(22a)

(22b)

式中:D1、D2为索1、索2响应近似解中的漂移项(此处仅考虑绝对漂移量);Av1、Av2为索1、索2响应近似解中不考虑漂移项后的响应幅值，称为无漂移幅值。β1与β2分别反映索1、索2的漂移项在响应幅值中所占的比重。

取f2/f1=1.11时，β1与β2随Ω的变化曲线如图10所示。

图10 β-Ω曲线Fig.10 The curves of β-Ω

由图10可知，β1与β2曲线在Ω<1.05时基本重合，且均约等于0，此时高阶解中几乎无漂移项，因此，图7中对应频率范围内两根拉索相位差很小；在Ω>1.10时β2明显大于β1，这是因为索力较小的索，漂移项的占比明显增大，进而导致图7中该频率范围内的瞬时相位显著增大。

综上所述，高阶近似项引起的相位差幅值大小受γ的影响不大，而高阶项中的漂移项的变化对瞬时相位的影响却有决定性作用，因此可利用β值的变化情况对瞬时相位差幅值作定性判断。

4 结 论

(1) 对比分析表明，Runge-Kutta法、非线性有限元法和多尺度法的结果具有较好的一致性，不同参数下，双索会呈现同步或异步振动的现象。

(2) 高阶近似项对拉索间的瞬时相位差有影响，相频分析时不能忽略，在一定频率下，甚至能使瞬时相位增大0.8π。进一步的分析表明：高阶近似项中相移值γ对瞬时相位差的贡献可以忽略，而漂移项对瞬时相位差却有决定性作用。

(3) 双索系统的瞬时相位差来源于线性解中相移值γ的差异以及高阶项中漂移项占比参数β的差异两个方面。