单元整体教学理念下的作业设计

刘江艳

单元作业在整体思维的引领下，注重各单元知识间的联系，强调从问题解决层面引导学生感悟知识的整体性，有利于学生形成良好的知识结构。笔者基于单元整体教学理念，从“课时内作业、跨课时作业、跨单元作业”三个维度，谈谈对作业设计的思考。

课时内、跨课时和跨单元三类作业的选题注重各单元知识间的关联，考查点分别指向基础夯实、知识迁移和能力提升，同时兼顾分层，以满足不同层次学生的学习需求。以下是学生分课时学习一元二次方程解法及根与系数的关系后，笔者设计的作业。

一、课时内作业设计策略

课时内作业针对每课时的重点知识和技能设计，是单元作业中的基础内容，面向全体学生。这部分作业旨在帮助学生梳理“一元二次方程”单元内相关知识点，宜选考查点相对单一的常规典型题，帮助学生巩固“双基”，訓练灵活解方程的能力。本单元知识点包含一元二次方程的定义和四种解法、根的判别式以及根与系数的关系等。据此，笔者在控制题目难度和体量的基础上，设计了以下作业。

1.下列方程是一元二次方程的是（   ）。

A.x²+y+3=0      B.3x²－2=0

C.x²+1/x=7        D.5x+3=0

2.若关于x的一元二次方程（a+1）x²+x+a²－1=0的一个根是0，则a的值为（   ）。

A.1     B.－1   C.±1      D.0

3.一元二次方程4x²+1=4x的根的情况是（   ）。

A.无实数根

B.只有一个实数根

C.有两个相等的实数根

D.有两个不相等的实数根

4.用配方法解方程x²+4x+1=0，配方正确的是（   ）。

A.（x－2）²=5      B.（x－2）²=3

C.（x+2）²=5     D.（x+2）²=3

5.已知α、β是一元二次方程x²+x-2=0的两个实数根，则α+β－αβ的值是__________________。

6.关于x的方程mx²－2x+3=0有两个不相等的实数根，那么m的取值范围是______________。

7.设x₁、x₂是一元二次方程x²－mx－6=0的两个根，且x₁+x₂=1，则x₁=__________，x₂=____________。

8.解方程：①3x²+5（2x+1）=0

②3（x－2）²=x（x－2） （用两种不同的方法解）

以上题目中，第1～7题涉及考点一元二次方程的定义、根的判别式、根与系数的关系、配方法等；第6、7题变换题型进一步巩固单元重点知识；第8题针对解方程的基本技能而设计，“用两种不同的方法解”旨在让学生感受方法选择的必要性。

二、跨课时作业设计策略

跨课时作业是将单元内各知识点融合起来进行综合考查的作业。与课时内作业相比，跨课时作业的综合性增强，难度有所提升，有利于促进学生形成知识网络，训练学生灵活应用知识解决问题的能力，从而完成对所学知识的迁移。

对于“一元二次方程”单元，方程解法是基本技能，解法与根的判别式不可分割；根与系数的关系与根的意义关系密切；解法、根的判别式、根与系数的关系均与一元二次方程的一般式紧密相连。笔者抓住这部分知识间的横向联系，关注解题方法的多样性，注意控制题目难度和深度，设计了如下作业。

9.已知关于x的一元二次方程x²+kx-6=0有一个根为-3，则方程的另一个根为___________。

10.已知等腰三角形ABC的两边AB、BC的长是关于x的方程x²－mx+m/2－1/4=0的两个实数根。①求证：无论m取何值，方程总有两个实数根；②如果三角形第三边AC的长为2，那么等腰三角形ABC的周长是多少？

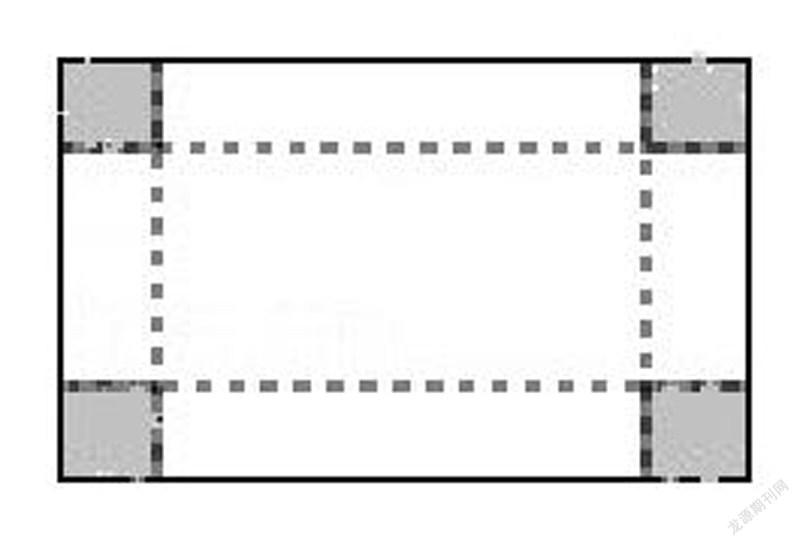
11.如下图，有一块矩形硬纸板，长30cm，宽20cm。在其四个角各剪去一个同样的正方形，然后将四周突出部分折起，可制成一个无盖长方体盒子。当剪去正方形的边长取何值时，矩形硬纸板剩下的面积为500cm²？当剪去正方形的边长取何值时，所得长方体盒子的底面积为200cm²？

从题意看，第9题是考查一元二次方程的根的意义，但其解法涉及解方程的技能、根与系数关系的理解，能体现以上知识点间的相关性；第10题将根的判别式、根与系数的关系以及根的定义等知识融合，并置于几何问题背景中，要求学生将几何问题转化为探究方程根的问题，再加以解决；第11题是方程的实际应用问题，其本质是探究方程的解是否符合题意，解决此题需要学生建立方程模型。

三、跨单元作业设计策略

跨单元作业是基于单元整体教学理念设计的、旨在培养学生数学核心素养的作业。该作业注重体现单元与单元知识间的联系，引导学生在问题解决中体会单元内容所蕴含的数学思想。

一元一次方程、一元一次不等式（组）、二元一次方程（组）以及一元二次方程等小单元归属于“方程与不等式”这个大单元。“方程与不等式”单元内容是学生学习初中数学的基本工具，为学生展开数学应用提供了基本模型，也是学生学习函数内容的重要基础。不仅如此，解二元一次方程（组）的“消元”和解一元二次方程的“降次”等方法都体现了化归的数学思想。笔者结合以上分析，重点围绕化归思想设计了3道作业题。以阅读探究题为例：

12.观察下列式子，完成后面的问题。

x²+4x+2=（x²+4x+4）－2=（x+2）²－2

∵（x+2）²≥0，∴x²+4x+2=（x+2）²－2≥－2，原式有最小值，是－2;

－x²+2x－3=－（x²－2x+1）－2=－（x－1）²－2

∵－（x－1）²≤0，

∴－x²+2x－3=－（x－1）²－2≤－2，原式有最大值，是－2。

问题：①求代数式－2x²+100x的最值；②解决实际问题“在紧靠围墙的空地上，利用围墙及一段长为100米的木栅栏围成一个長方形花圃（如下图），设长方形一边长x米，花圃的面积为S平方米。完成下列任务：用含x的式子表示花圃的面积S；说明当x取何值时，花圃的面积S为1200平方米？当x取何值时，花圃的面积S最大？最大面积是多少平方米？

这道题以阅读材料的方式呈现，为学生探究问题提供了支架。其内容融合了配方法和以实际问题为背景的最值问题，体现了方程与函数之间的关联性。解决问题①时，学生在阅读材料的提示下，利用“配方法”对代数式进行转化，求出代数式的最值，并在解决问题的过程中体会“配方法”所蕴含的化归思想。解决问题②时，学生先探究数量关系，列出关系式“-2x²+100x”，呈现函数模型“S=-2x²+100x”；接着针对“当x取何值时，花圃的面积为1200平方米？”的问题，构建一元二次方程模型“-2x²+100x=1200”，并计算解决；“当x取何值时，花圃的面积S最大？花圃的最大面积是多少平方米？”的问题是函数最值问题，学生将其巧妙地转化为问题①，即求代数式“-2x²+100x”的最值，问题解决便水到渠成。该题有一定的难度，适合学有余力的学生完成，或全班学生在教师的引导下完成。

一般来讲，课时内作业在课堂上完成，跨课时作业在课后完成，跨单元作业是选做作业。

（作者单位：襄阳市第三十五中学）

责任编辑  刘佳