Hoek-Brown屈服准则在岩质边坡稳定性分析中的应用对比

蒋正，祝斌

（杭州市勘测设计研究院有限公司，杭州 310012）

1 引言

近年来，岩质边坡稳定性问题一直为广大科研工作者研究的热点与难点。随着计算机技术的快速发展与应用，通过计算机的强大计算能力来对边坡的稳定性进行模拟计算已经成为人们分析边坡稳定性的一种可靠的手段与方法。Mohr-Coulomb准则原理相对简单便于应用，能够较为全面地反映岩体的强度特征，因此，是目前在岩土工程数值模拟中最常用的强度准则之一。但是该准则对低应力区、拉应力区和高应力区的岩体强度特性的解释存在不足，而Hoek-Brown屈服准则能够很好地弥补Mohr-Coulomb轻度准则在该方面的缺点，因此，利用Hoek-Brown屈服准则对岩体边坡稳定性分析与之对比具有一定现实研究意义[1-2]。

本文以华城矿露天矿山为研究背景，基于Mohr-Coulomb强度准则与Hoek-Brown强度准则的方法，通过FLAC 3D数值模拟的方式对该露天矿山的同一边坡进行数值模拟分析对比，根据边坡实际工程情况，比较两种强度准则在FLAC 3D数值模拟中的差异以及边坡的实际工程情况，以便更好地解决边坡稳定性问题。

2 工程背景

华成矿露天灰岩矿山Ⅰ区边坡位于该矿山采场北帮，地形位置属矿区地形最高处，采场位置属生产临时边帮逆层坡，南北方向长约403 m，东西方向宽为183 m，边坡最高点的高程为300 m，最低点高程为130 m，形成有8个台阶，已形成最高170 m垂高的边坡。边坡角40.52°，坡顶地形坡度+0°～-16°左右，最高点大于+320 m，属高危边坡，是该区研究的重点边坡体。

边坡岩体岩性主要为灰岩，均为弱含水层且岩体裂隙不发育，工程地质稳定性较好。根据边坡岩体现状与现场测试的实际情况确定边坡岩土体物理力学指标。岩体力学参数如表1所示。

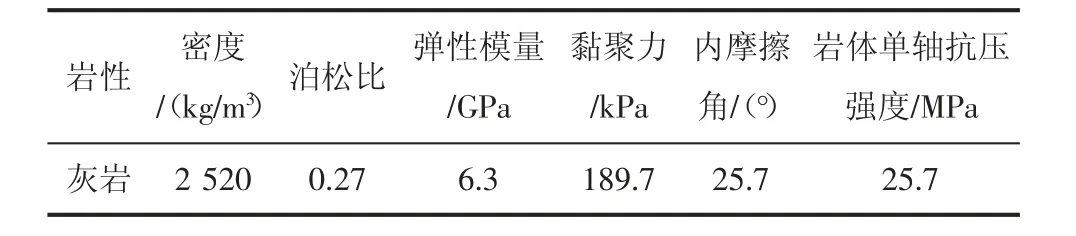
表1 Ⅰ区边坡体岩体力学参数

3 数值模型建立

根据华成矿露天矿Ⅰ区边坡的实际情况以及研究的实际要求，建立边坡开挖后的FLAC 3D计算模型，如图1所示。初始地应力只考虑重力作用，顶面设置为自由边界，其余边界条件均设置为位移约束，本构模型采用Mohr-Coulomb与Hoek-Brown两种本构模型共同计算分析对比。

图1 F LA C3D模型图

4 Hoe k-Br o w n准则参数确定

由于狭义Hoek-Brown强度准则的不足[3]，于1992年E.Hoek提出了修正后的Hoek-Brown强度准则也称为广义Hoek-Brown经验强度准则，并给出了个各类岩体经验参数值[4-5]。 表达形式为：

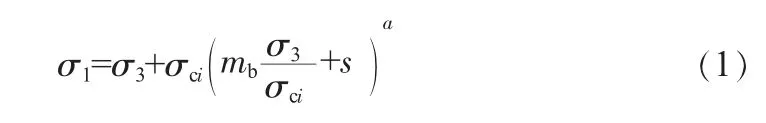
式中，mb为岩体的Hoek-Brown常量mi为组成岩体的完整岩块的Hoek-Brown常数；s、a与岩体特征有关的参数；σci为岩块单轴抗压强度，MPa；σ1、σ3是最大最小主应力，MPa。

对于经验参数m、s采用地质强度指标法（GSI）来进行确定，该矿区采取常规爆破的方式岩体扰动系数D可取1.0，根据矿区边坡特征情况查阅表格资料可以确定GSI=40、mi=7，边坡岩体Hoek-Brown准则参数计算如下：

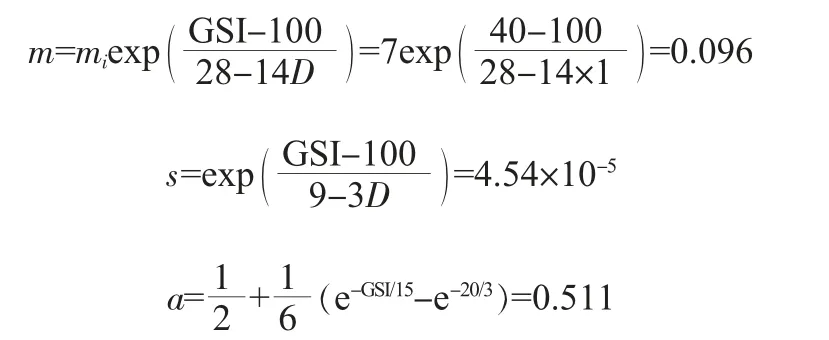
由已知岩体力学参数可求得参数值如表2所示。

表2 岩体力学参数表

5 计算对比分析

利用FLAC 3D自带Mohr-Coulomb与修正的Hoek-Brown本构模型来对边坡的稳定性进行模拟计算分析。在FLAC 3D中修正的Hoek-Brown本构模型可以利用SOLVE fos命令求解安全系数，通过对抗剪强度进行折减的方式来实现安全系数的求解。根据边坡的实际情况计算选取本构模型参数，经过数值模拟计算分别得到Mohr-Coulomb与Hoek-Brown两类分析图，并通过边坡的位移云图、应力云图、最大剪应变与位移矢量图几个方面来对边坡进行全面的分析对比[6-8]。

5.1 边坡位移

如图2～图5可知，边坡的水平位移与垂直位移的基本情况。由水平位移云图可以看出基于Hoek-Brown准则的边坡水平位移总体延呈层状增加，基于Mohr-Coulomb准则的边坡位移有明显集中于边坡体下部区域的情况。水平位移上可以看出基于Mohr-Coulomb准则的边坡最大水平位移量明显大于基于Hoek-Brown准则的位移量。由垂直位移云图可以看出基于Hoek-Brown准则的最大位移为0.294 m，基于Mohr-Coulomb准则最大位移量为0.226 m，小于Hoek-Brown准则下的位移量的大小。

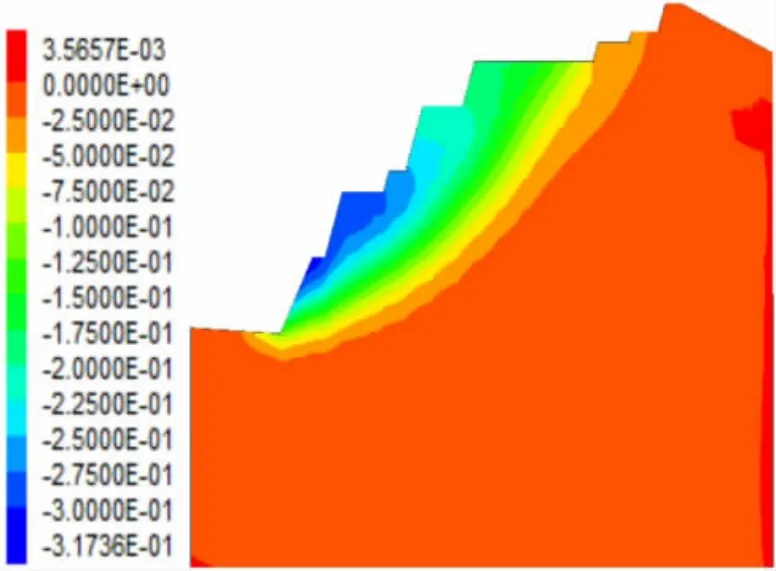
图2 水平位移云图（Mohr-Coulomb准则）

图3 水平位移云图（Hoek-Brown准则）

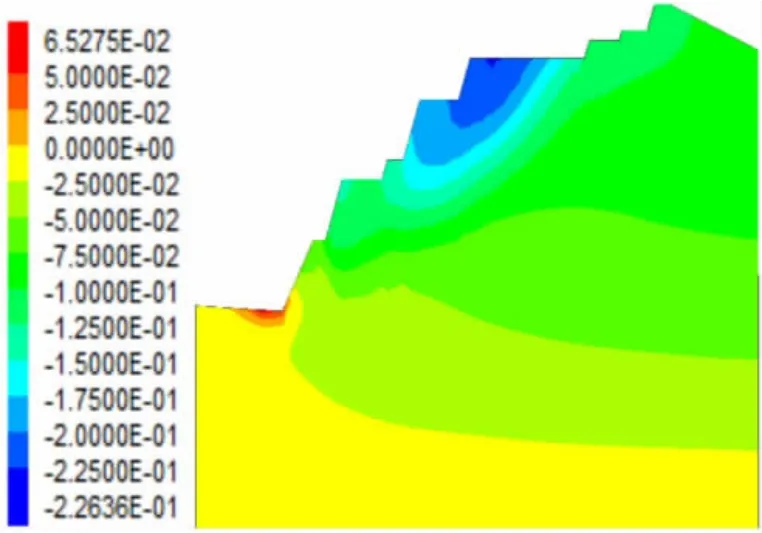
图4 垂直位移云图（Mohr-Coulomb准则）

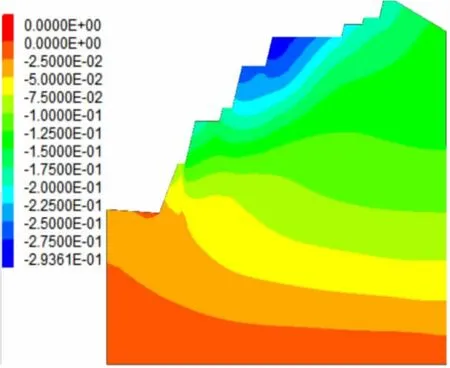
图5垂直位移云图（Hoek-Brown准则）

5.2 应力分析

如图6～图9可知，边坡的水平应力与垂直应力基本情况，可知在Mohr-Coulomb强度准则与Hoek-Brown强度准则下边坡的水平应力与垂直应力趋势基本一致。在坡脚处都出现应力集中现象，沿坡面向内部应力逐渐增大。通过图6与图7和图8与图9的对比可知，在同一位置处基于Hoek-Brown应力准则下的水平应力与垂直应力稍大于基于Mohr-Coulomb强度准则下的应力大小。

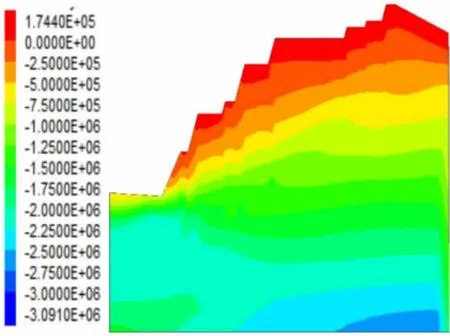
图6 水平应力云图（Mohr-Coulomb准则）

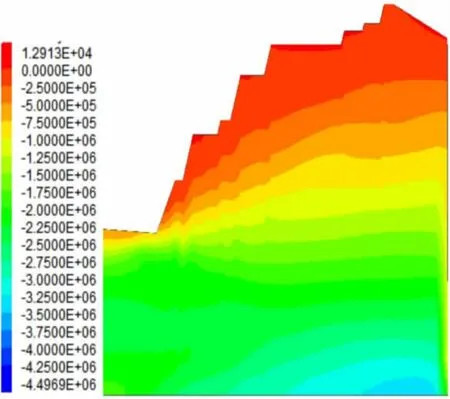
图7 水平应力云图（Hoek-Brown准则）

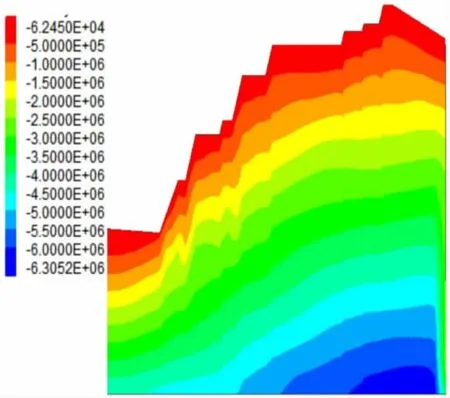
图9 垂直应力云图（Hoek-Brown准则）

5.3 最大剪应变

图10为基于Mohr-Coulomb强度准则的最大剪应变增量图，可以看出最大剪应变集中于边坡第一台阶的底部，形成了具有贯穿坡体的潜在滑动面；图11为基于Hoek-Brown应力准则下的最大剪应变增量图，可以看出最大剪应变集中于第二台阶边坡的底部。与图10相比具有明显的不同，且潜在的滑动面与图10相比不是那么明显，究其原因主要是边坡模拟计算采取的屈服准则不同因而出现两种不同的模拟计算结果。Mohr-Coulomb强度准则采用的是剪切屈服函数和非关联的剪切流动法则，而Hoek-Brown屈服准则流动参数与应力状态有关。

图10 最大剪应变增量图（Mohr-Coulomb准则）

图11 最大剪应变增量图（Hoek-Brown准则）

5.4 边坡的矢量位移与安全系数

针对文中实际的露天矿山边坡实际情况，采用FLAC3D来进行模拟计算分析。图12与图13分别为基于Hoek-Brown强度准则与Mohr-Coulomb强度准则下的位移矢量图，反映的是岩体质点的运动趋势。由图13可知在Hoek-Brown准则下的最大值为3.15×10-6，边坡上部分滑动位移的可能性比下部边坡更大；在Mohr-Coulomb准则下的最大值为1.68×10-6，边坡下部分滑动位移的可能性比上部边坡更大，因为基于Hoek-Brown强度准则能够考虑到拉应力以及结构面的影响岩体边坡破坏的情况，因此，位移矢量图中会有这样的差异。通过Hoek-Brown强度准则与Mohr-Coulomb强度准则分别求出边坡的安全系数为0.96与1.12，可知基于Hoek-Brown强度准则相对于Mohr-Coulomb强度准则所得到的安全系数相对要小。

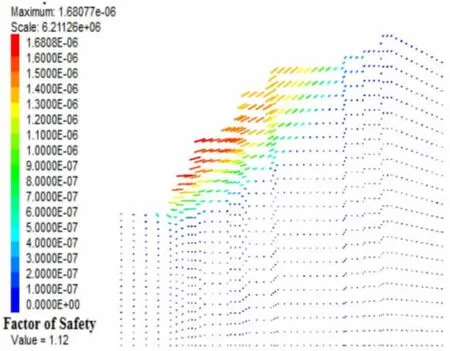
图12 位移矢量图（Mohr-Coulomb准则）

图13 位移矢量图（Hoek-Brown准则）

基于Hoek-Brown强度准则与Mohr-Coulomb强度准则的方法对华成矿露天灰岩矿山Ⅰ区边坡的数值模拟分析可以看出，该边坡的稳定性较差在边坡的底部出现了应力集中的现象，须要及时采取相应的工程措施对边坡进行加固或者削坡减荷，已确保边坡的稳定性与实际生产活动的安全。

6 结论

基于Hoek-Brown本构模型与Mohr-Coulomb本构模型在对边坡的稳定性分析数值模拟与实际的观测资料对比可以看出：

1）基于Mohr-Coulomb应力准则的水平位移主要集中于坡脚处，基于Hoek-Brown准则为沿坡面的位移最大，这与实际监测值中各台阶处位移量基本变化不大的情况基本相同，比较符合实际情况。在五台阶处垂直位移方向上可以看出基于Hoek-Brown准则下边坡的沉降量更大，更接近与实测值的26.5 cm。

2）两者在应力云图中都出现了应力集中的现象，对边坡的稳定性不利，基于Hoek-Brown准则的应力分布稍大于基于Mohr-Coulomb应力准则的数值模拟结果，但是差别不大。

3）最大剪应变增量图可以看在基于Mohr-Coulomb应力准则下形成了具有贯穿坡体的潜在滑动面，剪切破坏区明显小于基于Hoek-Brown应力准则下的破坏区域。这说明Mohr-Coulomb应力准则在边坡底部压应力区的剪切破坏的描述较好而在边坡上部处于拉张破坏区的模拟能力则不足，而基于Hoek-Brown应力准则的数值模拟分析则相对较好。

4）基于Hoek-Brown强度准则的边坡上部分矢量位移比较大，而基于Mohr-Coulomb强度准则计算结果则是下部边坡位移量大。由现场实际监测的情况与前者较为接近更符合边坡的实际情况，也由边坡的安全系数可知，基于Hoek-Brown强度准则考虑到边坡岩体结构面、节理等岩体的不完整性因素，因此，计算出的安全系数较为偏小。在边坡稳定性分析与设计中更偏安全。

Hoek-Brown强度准则与Mohr-Coulomb强度准则在边坡数值模拟分析中都有着自身的特点，基于Hoek-Brown强度准则在边坡的移动特征以及岩体强度所处应力状态更为符合边坡岩体的实际特征，对建设施工中的边坡具有一定的指导与借鉴意义。