能量开放场地中地层相对位移模型研究

杜修力,周 楠,赵 密,黄景琦,刘鹏程,苏驰翔

(1.北京工业大学城市与工程安全减灾教育部重点实验室,北京 100124; 2.北京科技大学土木与资源工程学院,北京 100083)

引言

近年来，随着我国基础设施建设的快速发展，大量地下结构工程得到大规模建设，如地铁隧道、地下车站、山岭隧道等。同时我国又处于欧亚地震带与环太平洋地震带之间，为强地震高发的国家。因此，在地下结构的运行周期内，保证其地震安全性是科学研究及工程设计的重要问题。

对于地下结构的抗震问题，目前已开展了大量的研究工作[1-4]，而合理且简便的实用抗震分析方法是这些研究所要达到的最终目标。通过现场观测、模型试验和理论分析表明，地下结构的地震响应受控于周围围岩土体的变形，结构在地震作用下随周围岩土体一起振动，其加速度、位移等结构响应与周围岩土体基本一致[5-6]。根据地下结构的地震响应特性，日本学者在20世纪70年代提出了将地层相对位移作为荷载的拟静力分析方法—反应位移法[7-9]。反应位移方法计算步骤简单明确，模型简单，是一种实用性很强的拟静力分析方法，在日本的地铁区间隧道、地铁车站和地下停车场等多种地下结构中得到了广泛应用，并写入日本相关设计规范中，如《大型地下结构抗震设计指南》等[10]。我国多部规范也采用了反应位移方法作为地下结构地震响应分析的分析方法之一，如《城市轨道交通抗震设计规范》《城市轨道交通工程设计规范》等[11-12]。在反应位移方法中，地震荷载包括土层相对位移对结构产生的地震土压力、结构周围土层对其的剪切力和结构本身在地震作用下的惯性力。周围土层对结构的约束作用通过地基弹簧进行模拟。图1给出了经典反应位移方法示意。

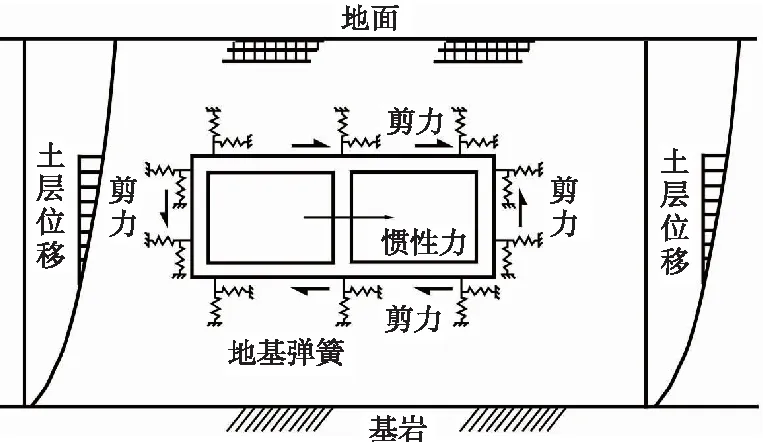
图1 经典反应位移方法示意

在反应位移方法[13-15]中，地震作用主要通过地震作用下的地层变形实现，地层变形模式的假设是否合理直接决定了反应位移方法的准确性。在日本《大型地下结构抗震设计指南》中，基于建设地下结构所在的表层地基反应位移为基岩以上土层的一阶模态的假设，推导出地层位移沿深度方向按余弦函数分布，给出了基于基岩速度设计谱的位移分布函数。我国《城市轨道交通抗震设计规范》中同样假设地层位移按照余弦函数分布，但这些位移模型的提出是基于假定设计地震基准面为刚性基岩面，其上覆土层等效为能量半封闭的系统(即在水平方向上能量开放，但在竖直方向上能量封闭的系统)，地震动从基岩面传入土层内很难再传输出去，基岩以上土层场地响应可近似等效为单自由度的一维振动响应。这种假设对于大部分城市的土层场地是合理的，但作为沉积土层，往往在土层底部会遇到波阻抗突然增大的岩石层。随着城市轨道交通的快速发展，实际工程中遇到了很多场地条件难以等效为能量半封闭的情况，如金安桥地铁车站其土层波阻抗沿着深度方向并未出现明显增大情况；京张高铁八达岭车站完全建设于山体之中等。对于这种情况，很难再将地下结构所在场地的地震响应问题等效为能量半封闭的体系，其实际上为一种能量开放体系。对于可等效为能量开放的场地，继续使用规范中给出的余弦函数的位移分布模式和设计地震基准面的选取方法进行反应位移方法抗震设计将带来很大的不合理性。因此，需要针对能量开放场地的位移场响应进行系统研究，以提出适用于此类场地的地层位移模型。

本文将水平均匀半空间能量开放系统在地震动垂直入射时的场地响应问题等效为应力波的一维传播问题。通过一维土柱模型模拟场地土的动力响应特性，模型顶部为自由表面，底部设置黏性人工边界，地震动输入通过等效节点力的方式进行输入。模拟不同场地类别、地震烈度等级及近远场效应下场地的位移响应，最终提出能量开放体系的一种地层位移模型。

1 能量开放场地的地震响应分析模型

对于均匀水平半空间场地，在地震动垂直入射情况下，其地震响应可简单等效为一维土柱模型进行分析。建立的一维土柱模型如图2所示。

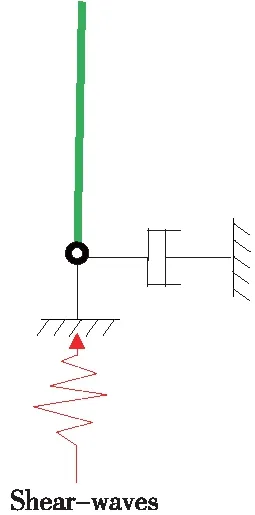
图2 能量开放场地一维计算模型

考虑辐射阻尼效应，在一维土柱模型底部施加黏性边界，黏性边界的阻尼系数为

CT=ρcs

(1)

为实现一维土柱的波动输入，在杆件底部施加等效节点力F(t)，则

(2)

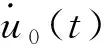
为合理研究不同围岩等级情况下能量开放场地的地震动响应，针对Ⅲ、Ⅳ、Ⅴ级围岩场地进行分析，各级围岩基本参数如表1所示。

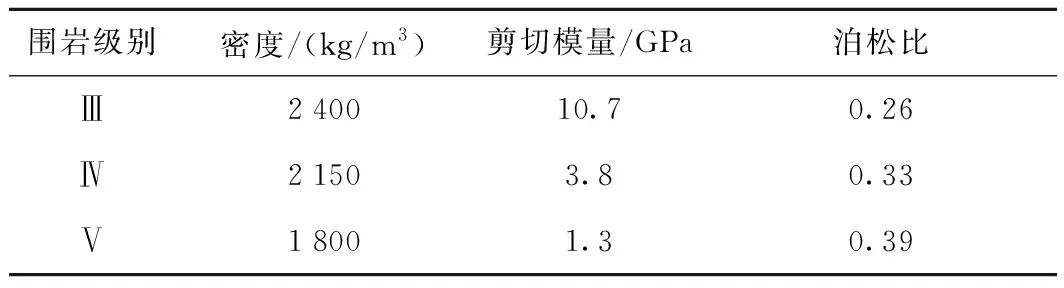
表1 场地材料参数

2 输入地震动及模拟工况

地震动为人工合成地震动，选取反应谱为GB20909—2014《城市轨道交通结构抗震设计规范》中给出的加速度设计反应谱，见图3。结构阻尼比取ξ=0.05，参数η和γ分别取1.0。

对于规范中给出的设计地震动加速度反应谱特征周期Tg，对于同一类场地在3个不同反应特征周期分区(0.35 s区、0.40 s区和0.45 s区)具有不同的Tg值。本研究取3个分区的Tg平均值作为每类场地的特征周期。选取的特征周期Tg见表2。

表2 本研究选取的反应谱特征周期Tg s

为描述地震地面运动从开始、强震段、自然衰减的全过程，采用经典的非平稳模型[16]

F(t)=f(t)A(t)

(3)

式中，f(t)为非平稳强度函数，其函数形式为

(4)

式中，tb=0.5Ts；tc=1.2Ts；c=2.5/Ts。其中，Ts为平稳持时，其取值参照文献[17]中结果取值。

图4给出Ⅳ类场地在设计烈度为7度情况下，1条人工合成地震动的时程曲线。

图4 人工合成地震动时程曲线

3 结果分析

对于每一类场地条件，抗震设防烈度分别设为6度、7度、8度和9度。输入地震动在合成时区分近场和远场的区别。每个工况共计算90条人工地震动，通过数理统计的方法获得不同场地条件及不同设防烈度下能量开放体系中地层的峰值剪应变分布规律。

3.1 Ⅲ级围岩条件不同设防烈度下峰值剪应变分布规律

图5、图6分别给出了不同设防烈度下，Ⅲ级围岩场地的峰值剪应变随埋深的分布规律。从图5、图6中可以看出，随着深度增加，在各级设防烈度下的峰值剪应变均先增加后减小，直到基本保持不变，并且在各级设防烈度下，峰值剪应变的拐点深度位置大致相同。同时，设防烈度的增加会使得峰值剪应变增大，衰减至平稳状态的深度值更大。在同一设防烈度下，近场地震动引起的最大剪应变要略大于远场地震动引起的峰值剪应变。

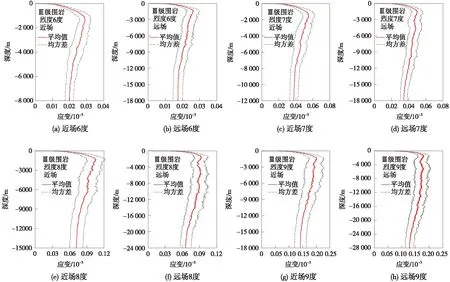
图5 不同设防烈度下峰值剪应变分布规律

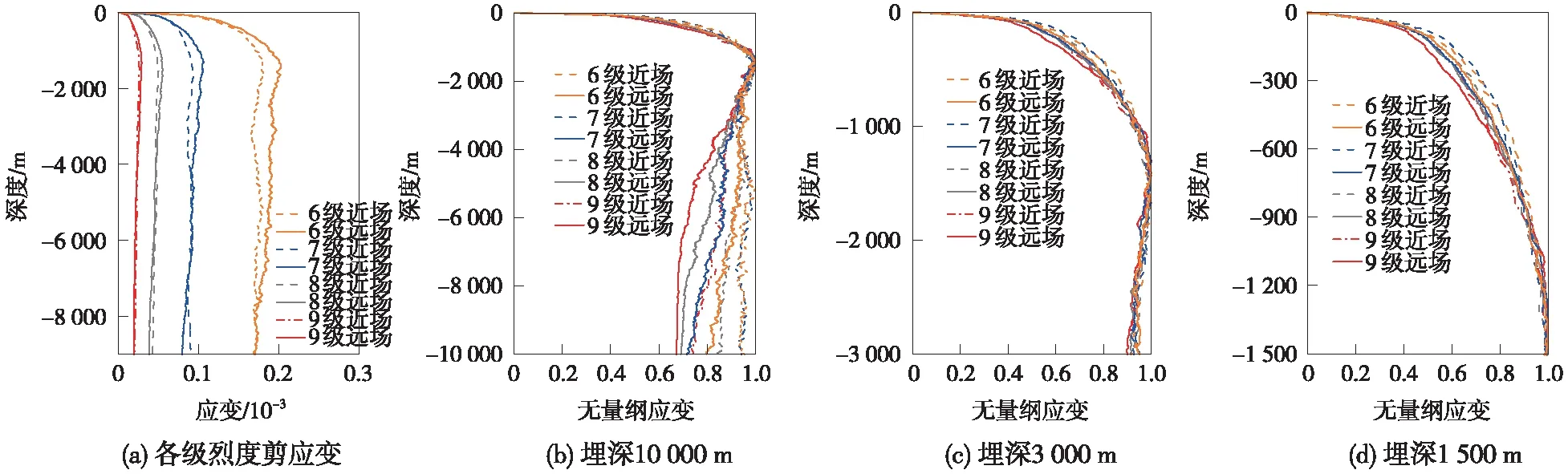
图6 各级设防烈度下峰值剪应变及无量纲化峰值剪应变

3.2 Ⅳ级围岩条件不同设防烈度下峰值剪应变分布规律

图7、图8分别给出了不同设防烈度下，Ⅳ级围岩场地的峰值剪应变随深度变化的分布规律。从图7、图8中可以看出，不同设防烈度情况下的峰值剪应变均随埋深增加呈先增大后减小趋势，直到基本保持不变。各设防烈度情况下，峰值剪应变的拐点埋深大致相同。同时，设防烈度的增加会使得峰值剪应变增大，衰减至平稳状态的深度值增加。在同一设防烈度下，近场地震动引起的最大剪应变要略大于远场地震动引起的峰值剪应变。

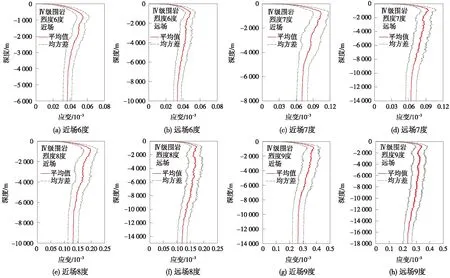
图7 不同设防烈度下峰值剪应变分布规律

图8 各级设防烈度下峰值剪应变及无量纲化峰值剪应变

3.3 Ⅴ级围岩条件下不同设防烈度下峰值剪应变分布规律

图9、图10分别给出了不同设防烈度下，Ⅴ级围岩场地的峰值剪应变随深度变化的分布规律。从图9、图10中可以看到，随着深度增加，不同设防烈度情况下峰值剪应变的变化规律均先增加后减小，直到基本保持不变。各设防烈度情况下，峰值剪应变的拐点埋深大致相同。同时，设防烈度的增加会使得峰值剪应变增大，衰减至平稳状态的深度值增加。在同一设防烈度下，近场地震动引起的最大剪应变要略大于远场地震动引起的峰值剪应变。

图9 不同设防烈度下峰值剪应变分布规律

图10 各级设防烈度下峰值剪应变及无量纲化峰值剪应变

3.4 不同围岩级别转折深度值对比

图11给出了无量纲化后的剪应变在不同场地条件及不同设防烈度下转折深度值规律。从图11中可以看出，在同一抗震设防烈度条件下，不同围岩场地的转折深度和下降斜率基本一致。因此，可以用一个统一公式对不同场地条件及不同设防烈度下的峰值剪应变进行描述。

图11 不同场地条件及不同设防烈度下转折深度值规律

3.5 参数拟合

针对剪应变随深度与转折深度比值的变化规律进行参数拟合，得到拟合公式

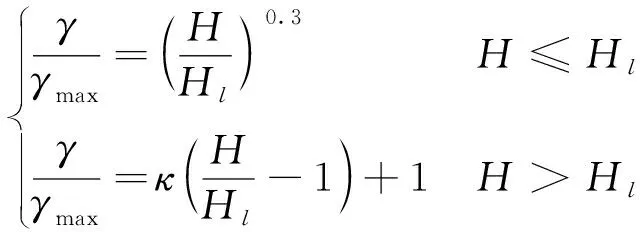
(5)

式中，γ为剪应变；H为埋深；γmax为埋深各点最大剪应变，其值见表3；Hl为应变沿深度方向增减拐点深度，其值见表4；κ为图12中峰值点后直线斜率，其值见表5。

表3 γmax取值 ×10-3

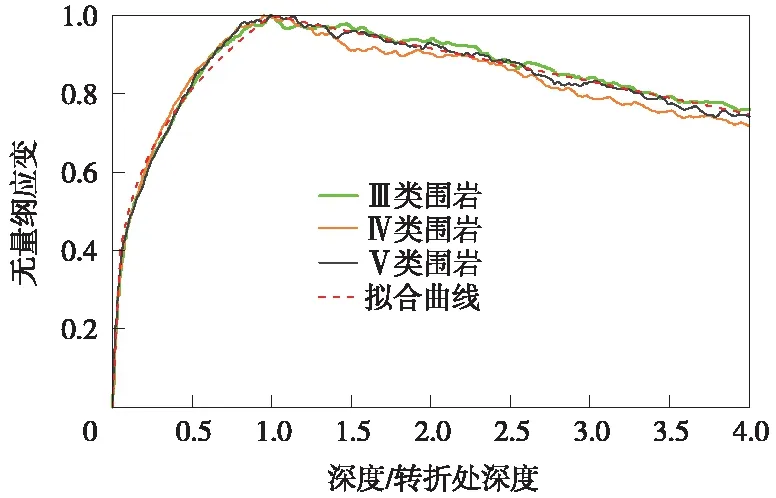
图12 剪应变随深度与转折深度比值变化规律

表4 拐点埋深Hl m

表5 斜率κ

式(5)能很好地反映在不同场地条件及不同设防烈度下，峰值剪应变随深度与转折深度比值的变化规律，拟合曲线如图12所示。

4 结论

针对均匀半空间能量开放场地的围岩地震动响应规律进行了研究，分析了不同场地条件及不同设防烈度下峰值剪应变分布规律，并对其转折深度值的规律进行了进一步分析。研究考虑了场地类别、设防烈度和近、远场效应等影响，主要结论如下。

(1)在能量开放的场地中，其地层剪应变模式并非按照余弦函数的形式分布。

(2)研究提出不同场地条件及不同设防烈度下峰值剪应变分布规律。模拟结果表明，在均匀半空间能量开放场地围岩的地震动响应随着深度的增加先增大后减小，最后趋于平均。在同一场地条件下，地震峰值加速度越大地震动响应越大。在同一地震峰值加速度条件下，场地类别越好则围岩的地震动响应越小。

(3)研究提出不同场地条件及不同设防烈度下剪应变随深度与转折深度比值的变化规律，在同一抗震设防烈度条件下，不同围岩场地的转折深度和下降斜率基本一致，同时根据模拟结果对其进行参数拟合。研究发现，在Ⅴ类围岩场地条件时，拐点深度为500 m；在Ⅳ类围岩场地条件时，拐点深度为850 m；在Ⅲ类围岩场地条件时，拐点深度为1 500 m。