三峡库区黄土坡滑坡滑带土直剪应力松弛特征试验研究

2020-04-20杨林筱陶现雨

安全与环境工程 2020年1期

陈琼，杨林筱，陶现雨

(中国地质大学(武汉)工程学院，湖北武汉 430074)

土的流变性主要包括以下几个方面：蠕变特性、松弛特性、流动特性和长期强度。应力松弛是岩土材料应变一定时，应力随时间而逐渐减小的现象。应力松弛是岩土材料常见的流变特性之一，大量岩土工程项目中存在岩土体应力松弛现象，例如隧道工程、基坑工程和滑坡工程中支护结构与围岩相互作用过程的应力松弛现象[1-5]。岩土体的应力松弛特性对滑坡支护结构的长期稳定性具有重要影响[6-7]。岩土体的应力松弛类型可分为非完全松弛和完全松弛两种类型[8-9]。岩土体的应力松弛量与其垂直压力有关，岩土体的埋深越大，其开挖后应力松弛量越大[10]。为了更加准确地描述岩土体的应力松弛特征，研究者们提出了各种岩土体应力松弛模型[11-13]。目前一些研究者多采用室内三轴试验[14]、直剪试验[15]等，研究不同应变水平、不同固结条件下岩土体的应力松弛特征。如张春晓等[16]以南宁膨胀土为例，采用弹性与黏弹性元件串联来描述膨胀土的应力松弛特性，该模型可以正确模拟膨胀土应力松弛的全过程；汪明武等[17]以非饱和石灰改良膨胀土为例，采用GDS非饱和三轴应力路径系统获取了其应力松弛曲线，并针对获得数据的振荡变化特点，引入经验模态分解理论研究了改良膨胀土应力松弛过程的波动特性；王志俭等[18]以安乐寺滑坡滑带土为例，采用GDS非饱和土三轴试验系统对滑带土应力松弛特征进行了试验研究，推导出了滑带土应力松弛模型；Paraskevopoulou等[4]以灰岩为例，采用轴向加压设备对灰岩应力松弛特征进行了试验研究，通过灰岩径向应变与应力的变化曲线确定了灰岩应力松弛量与垂直压力呈指数关系；赵振华等[19]开展了含卸压孔的硬岩在峰前加载、松弛、再加载和再松弛模式下的应力松弛试验，得出其峰前应力松弛特征。

综上研究可见，针对不同的岩土体，采用不同的试验方法得出的岩土体应力松弛模型不尽相同。特别是在滑坡的稳定性分析和计算中，经常采用抗剪强度指标来进行计算和反演，工程实践中积累了丰富的数据和经验关系。目前采用三轴试验对滑坡滑带土应力松弛特征进行的研究较多，而采用直剪仪对滑带土应力松弛特征研究的试验结果非常少，因此研究滑坡滑带土在不同的垂直压力、应变条件下的剪应力松弛特征则非常必要。基于此，本文以三峡库区黄土坡滑坡滑带土为例，开展了该滑坡滑带土直剪应力松弛特征的试验研究，研究结果对滑坡的长期稳定性计算和支挡结构的设计具有一定的指导意义。

1 工程概况

图1 黄土坡滑坡1#崩滑堆积体平面图Fig.1 Plan view of No.1 collapse and sliding accumu- lation mass of Huangtupo landslide

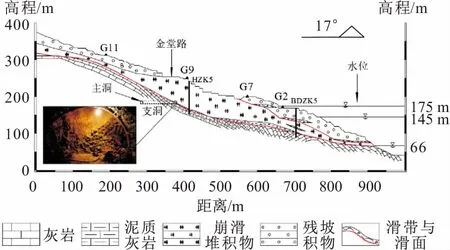
图2 黄土坡滑坡典型剖面图Fig.2 Typical crosssection of Huangtupo landslide

黄土坡滑坡位于湖北省恩施土家族苗族自治州巴东县，根据勘察资料，该滑坡由临江1#崩滑堆积体、临江2#崩滑堆积体、园艺场滑坡和变电站滑坡组成[20]，面积为135×104m2，体积为6 934×104m3，属于特大型滑坡。为了研究该滑坡的演化机理和防治措施，2010年2月中国地质大学(武汉)在黄土坡滑坡临江1#崩滑堆积体上修建了巴东野外大型综合试验场，其主要包括1条穿过滑体、滑带和滑床的试验主隧洞和5条试验支洞，见图1。试验主隧洞全长908 m，1#、4#支洞洞深为5 m，2#支洞洞深为10 m，3#支洞洞深为145 m，5#支洞洞深为40 m。临江1#崩滑堆积体代表性纵剖面见图2。在3#支洞揭露滑带土，滑带土埋深在20～50 m之间，为了研究原位滑带土的流变特性，沿滑带走向开挖试验平洞，然后进行原位剪切试验。在进行原位剪切试验时，需要安装压力盒、位移计、孔隙水压力计等量测仪器，但在安装这些仪器时发现该滑坡滑带土存在应力松弛现象，导致传感器的初始值在缓慢地变动。鉴于此，本文重点开展黄土滑坡滑带土的剪切应力松弛试验。

2 材料与方法

本次试验样品取自黄土坡滑坡3#支洞试验平洞内的滑带土，其基本物理性质指标见表1。

表1 黄土滑坡3#支洞试验平洞内滑带土的基本物理性质指标

注：括号内数据为平均值。

为了更真实地模拟现场条件下该滑坡滑带土的物理状态，将试样按如下方法制备：首先人工剔除滑带土中大于2 mm的颗粒，再根据滑带土的含水状态配成19.16%含水率的湿土，置于保湿缸中静止24 h以上备用；然后根据原状样试验结果，将备用湿土按天然密度为2.07 g/cm3制成环刀样，试样直径为61.8 mm、高度为20 mm；最后将制好的试样放入真空饱和缸中，抽真空4 h，再注入去离子水浸泡24 h。

本次直剪试验采用南京宁曦仪器有限公司生产的四联等应变直剪仪，轴向荷载由砝码施加，剪应变由电机控制；垂直位移和水平位移由位移传感器测量并由数据采集器记录，数据采样间隔为10 s。

为了研究不同埋深的滑带土应力松弛特征和变化规律，将滑带土试样分别在100 kPa、200 kPa、400 kPa、800 kPa垂直压力下排水固结，直至垂直变形不大于0.01 mm/h；然后以0.02 mm/min的剪切速率分级施加剪切应变。为了研究峰值强度前后滑带土的应力松弛特征，控制剪应变分别为1.62%、3.24%、4.85%、6.47%、8.09%、9.71%、11.33%、12.94%，达到目标剪应变后停止剪切，保持剪应变不变，记录滑带土应力松弛数据，每级剪应变持续24 h后再加载下一级剪应变。

3 结果与分析

3.1 滑带土应力松弛总体特征

为了便于讨论，定义某级恒应变条件下滑带土松弛开始时的剪切应力τmax与松弛24 h后的剪切应力τmin之差为应力松弛量Δτ，残余应力比为k=τmin/τmax，松弛应力比为R=Δτ/τmax。以剪切位移增量1 mm、剪切速率0.02 mm/min、应力松弛时间24 h为例，绘制4组滑带土在不同垂直压力(σn)下剪切应力与时间的关系曲线，见图3。

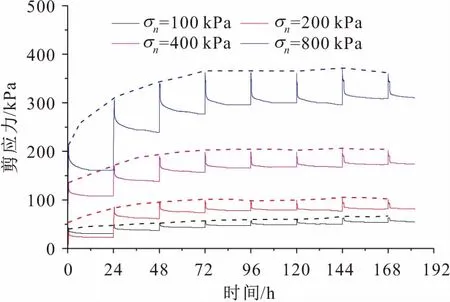
图3 不同垂直压力下滑带土剪切应力与时间的关系曲线Fig.3 Stress relaxation and time of sliding zone soil with different vertical pressure注：图中虚线代表剪应力最大值包络线。

由图3可见，随着垂直压力的增加，滑带土剪切应力不断增加；随着剪应变的增加，滑带土剪切应力表现出轻微的应变软化趋势。

通过滑带土各级应变下剪切应力的最大值和松弛24 h后的稳定剪切应力值，可以得到不同垂直压力下滑带土的峰值强度指标和稳定松弛强度指标，分别为cmax、φmax和cmin、φmin，其结果见表2。

由表2可知，滑带土的稳定松弛强度指标约为峰值强度指标的78.31%和85.65%，说明应力松弛对滑带土黏聚力的影响较对内摩擦角的影响更大，这是因为滑带土的应力松弛过程是以黏弹性为主，当应变一定且应力松弛后，黏性有减弱的趋势。

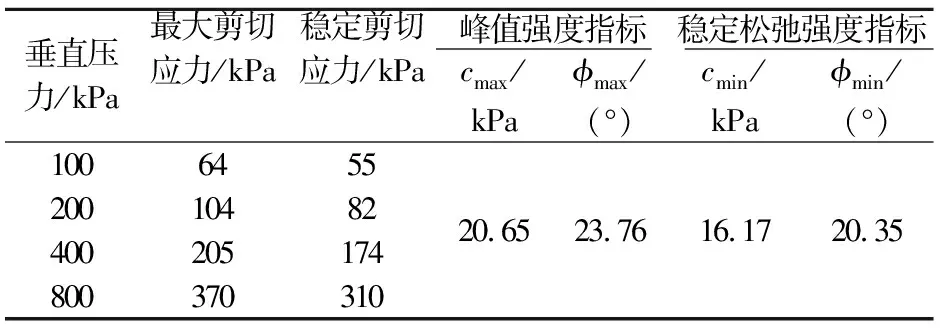
表2 滑带土的直剪强度指标

3.2 滑带土应力松弛过程中剪应力与时间的关系

为了研究滑带土应力松弛过程中剪应力随时间的变化，以垂直压力σn=800 kPa为例，对不同剪应变下滑带土的应力松弛曲线进行了研究，其结果见图4。

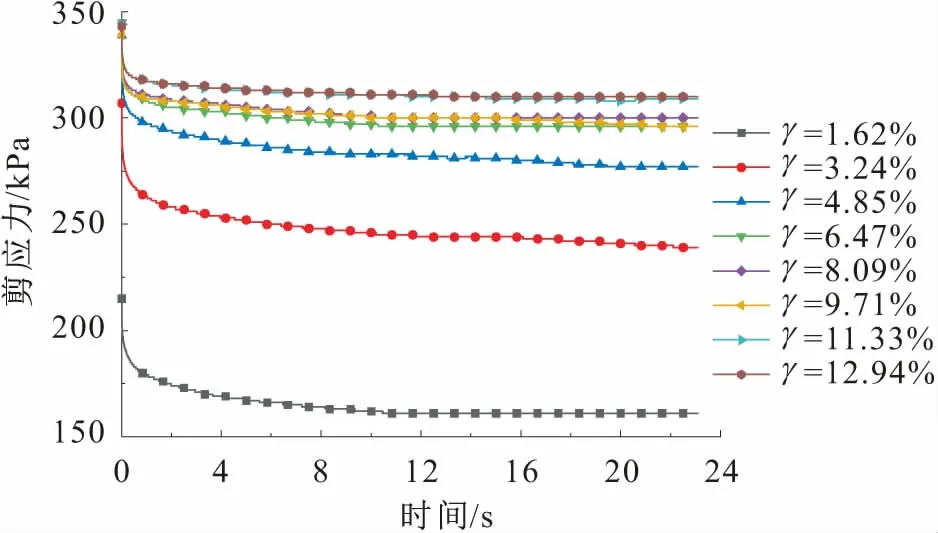
图4 不同剪应变下滑带土的应力松弛曲线(σn=800 kPa)Fig.4 Stress relaxation curves of sliding zone soil with different shear strain (σn=800 kPa)

由图4可见：应力松弛初期，滑带土的剪应力衰减较快，随着时间的增加，应力松弛过程趋于稳定；当剪应变(γ)超过6.47%之后，滑带土的应力松弛曲线几乎相同。

为了研究滑带土应力松弛量所占的百分比，以垂直压力σn=800 kPa为例，对滑带土的应力松弛曲线进行了归一化处理，其结果见图5。

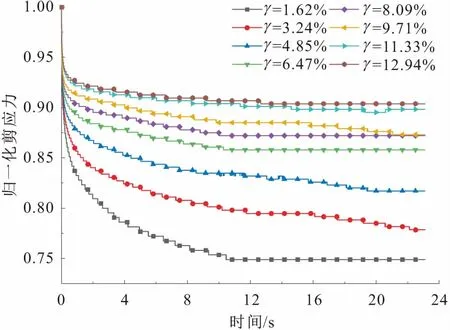
图5 不同剪应变下滑带土的归一化应力松弛曲线 (σn=800 kPa)Fig.5 Normalized stress relaxation curves of sliding zone soil with different shear stain (σn=800 kPa)

由图5可见：随着剪应变的增大，滑带土应力松弛曲线存在明显的转折点，转折点之前滑带土的应力松弛速率快速降低，转折点之后滑带土的应力松弛速率缓慢降低或趋近于水平;随着剪应变的增大，滑带土的残余应力比k增大，最终趋于0.90。

3.3 滑带土的应力松弛量和应力松弛比

不同垂直压力下滑带土应力松弛量与剪应变的关系曲线，见图6。

图6 不同垂直压力下滑带土应力松弛量与剪应变的关系曲线Fig.6 Stress relaxation amount and shear strain of sliding zone soil with different vertical pressure

由图6可见，随着垂直压力的增大，滑带土的应力松弛量逐渐增大；随着剪应变的增大，滑带土的应力松弛量呈先增加后减小的趋势。

不同剪应变下滑带土应力松弛量与垂直压力的关系曲线，见图7。

图7 不同剪应变下滑带土应力松弛量与垂直压力的关系Fig.7 Stress relaxation amount and vertical pressure of sliding zone soil with different shear stain

由图7可见，滑带土的应力松弛量与垂直压力为线性关系，且其曲线斜率随着剪应变的增大而减小。

不同垂直压力下滑带土应力松弛比与剪应变的关系曲线，见图8。

图8 不同垂直压力下滑带土应力松弛比与剪应变的关系曲线Fig.8 Stress relaxation ratio and shear strain of sliding zone soil with different vertical pressure

由图8可见，滑带土的应力松弛比整体上随着剪应变的增大呈递减的趋势。

4 讨论与分析

4.1 滑带土非线性应力松弛经验模型——双指数衰减模型

类似于土的蠕变曲线阶段划分，有的学者尝试将滑带土的应力松弛曲线人为地划分为三部分：瞬间松弛阶段、衰减松弛阶段和稳定松弛阶段[15,21]。这样划分的好处是可以对滑带土的应力松弛曲线进行细分，能够反映滑带土弹性阶段、弹黏性阶段，不便之处是建立滑带土应力松弛模型时需要的参数较多，且三个阶段拐点的划分界限不是很严格。本文通过对大量试验数据的分析发现，如果以应力松弛曲线曲率最大点(T)为分界点，滑带土的应力松弛曲线可以减少成两段式划分，所需的试验参数较少，拟合效果较好，划分界限的求解具有唯一性。以垂直压力为800 kPa、剪应变γ=12.94%的滑带土应力松弛曲线(见图9)为例，可知以曲率最小点(t=0.88 h)为分界点可将滑带土应力松弛曲线分为两个松弛阶段：第I松弛阶段时间较短，约占总时间的12.33%，应力松弛速率较快，且其速率的衰减也较快，应力松弛量约占总松弛量的74.14%，这一阶段滑带土的应力松弛以弹塑性为主；而第II松弛阶段持续时间则较长，应力松弛速率较慢，且其速率的衰减逐渐减小，应力松弛量约占总松弛量的25.86%，这一阶段滑带土的应力松弛以黏塑性为主。根据应力松弛曲线的变化趋势可知，该滑带土应力松弛量随着时间的延长会趋向于某一固定值，表现出非完全应力松弛的特征。

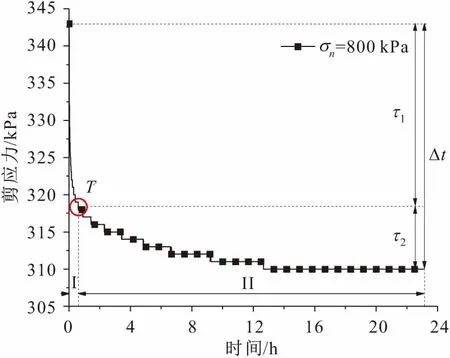
图9 剪应变为12.94%时滑带土的应力松弛曲线 (σn=800 kPa)Fig.9 The stress relaxation curve of sliding zone soil at shear strain of 12.94%(σn=800 kPa)

根据滑带土应力松弛曲线的特点，将其划分成两段以后，可采用双指数衰减模型来描述滑带土应力松弛过程中剪切应力与时间的关系：

τ(t)=τ0+A1e-t/b1+A2e-t/b2

(1)

式中：τo为t=∞时滑带土的残余剪切应力；A1、A2为与滑带土两阶段应力松弛量有关的参数；b1、b2为与滑带土两阶段持续时间有关的参数。各参数均由试验确定。

本文利用Matlab软件，采用双指数衰减模型对滑带土的应力松弛试验曲线进行了拟合，其拟合结果见表3。

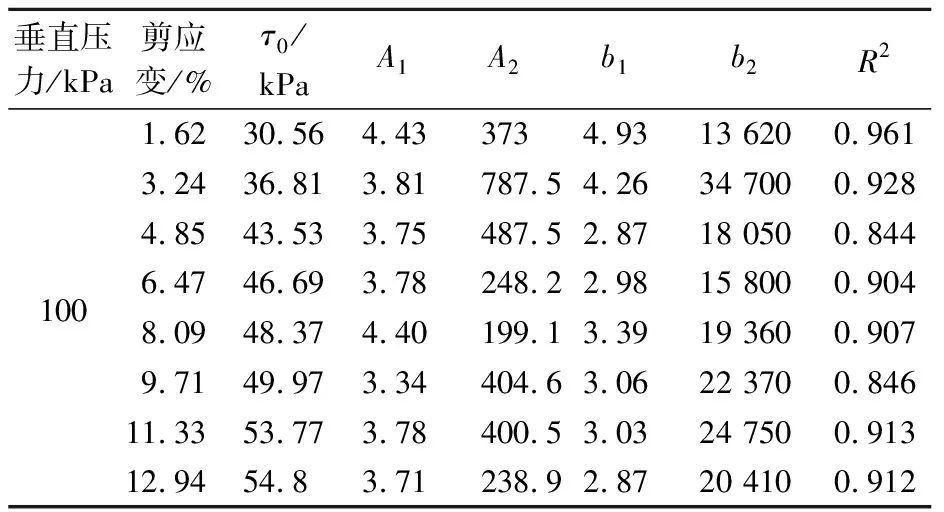
表3 双指数衰减模型对滑带土应力松弛曲线的拟合结果

续表3

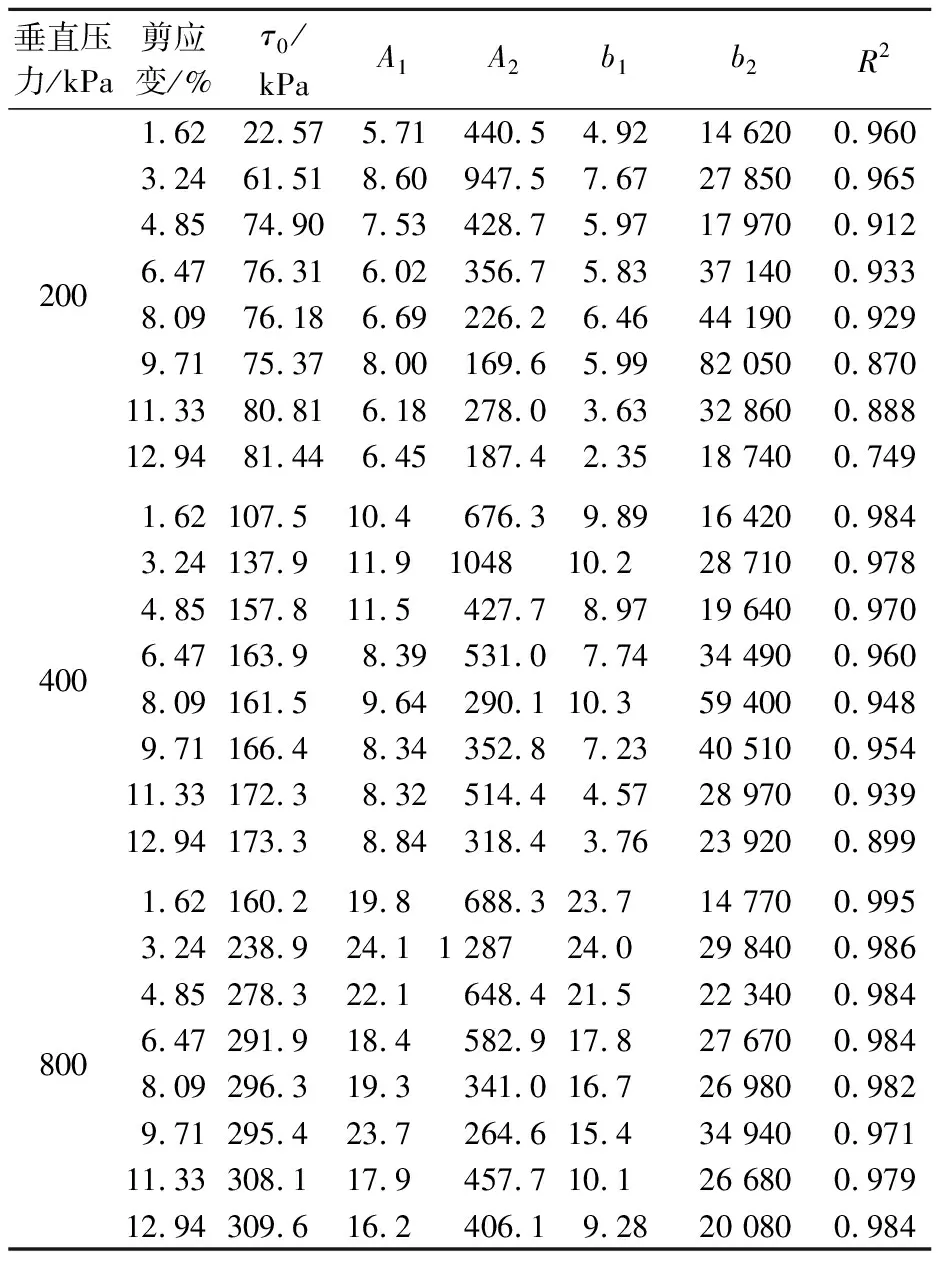
垂直压力/kPa剪应变/%τ0/kPaA1A2b1b2R21.6222.575.71440.54.9214 6200.9603.2461.518.60947.57.6727 8500.9654.8574.907.53428.75.9717 9700.9126.4776.316.02356.75.8337 1400.9332008.0976.186.69226.26.4644 1900.9299.7175.378.00169.65.9982 0500.87011.3380.816.18278.03.6332 8600.88812.9481.446.45187.42.3518 7400.7491.62107.510.4676.39.8916 4200.9843.24137.911.9104810.228 7100.9784.85157.811.5427.78.9719 6400.9706.47163.98.39531.07.7434 4900.9604008.09161.59.64290.110.359 4000.9489.71166.48.34352.87.2340 5100.95411.33172.38.32514.44.5728 9700.93912.94173.38.84318.43.7623 9200.8991.62160.219.8688.323.714 7700.9953.24238.924.11 28724.029 8400.9864.85278.322.1648.421.522 3400.9846.47291.918.4582.917.827 6700.9848008.09296.319.3341.016.726 9800.9829.71295.423.7264.615.434 9400.97111.33308.117.9457.710.126 6800.97912.94309.616.2406.19.2820 0800.984

由表3可知，采用双指数衰减模型对滑带土应力松弛试验曲线进行拟合的精度较高，R2平均值介于0.901～0.984之间。

将垂直压力为800 kPa、剪应变为12.94%时滑带土应力松弛的试验曲线与双指数衰减模型的拟合曲线进行对比，其结果见图10。

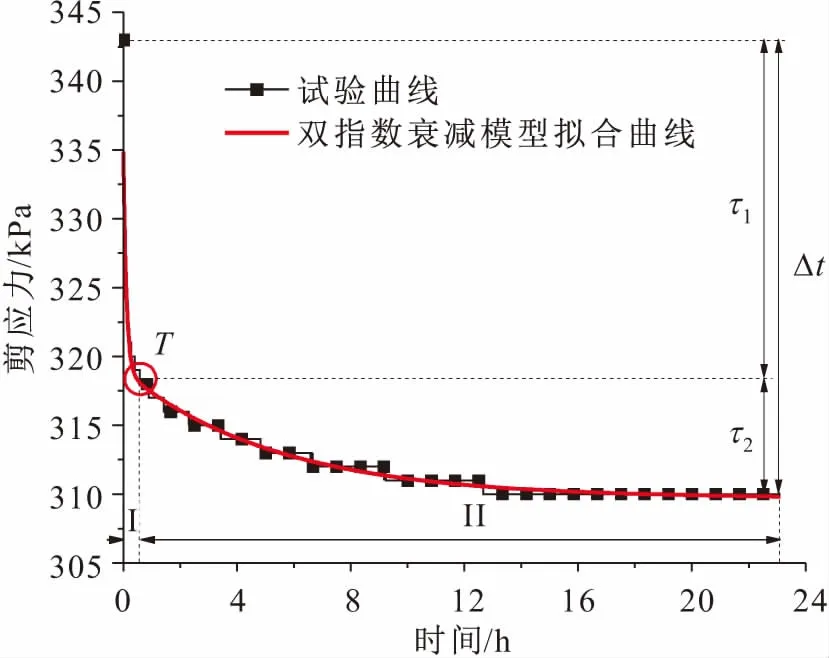
图10 剪应变为12.94%时滑带土应力松弛试验曲线与双指数衰减模型拟合曲线的对比(σn=800 kPa)Fig.10 The test and fitting curve of stress relaxation of sliding zone soil at shear strain of 12.94% (σn=800 kPa)

由图10可见，滑带土应力松弛双指数衰减模型的拟合曲线与试验曲线有较好的吻合度，能够正确地反映滑带土应力松弛曲线的基本特点。

4.2 滑带土双指数应力松弛特征

通过滑带土应力松弛双指数衰减模型的拟合曲线，能够以T点为分界点定量地划分滑带土两个松弛阶段，进而可以精确地计算出不同的垂直压力、剪应变条件下滑带土应力松弛拐点(T点)对应的时间，见图11。

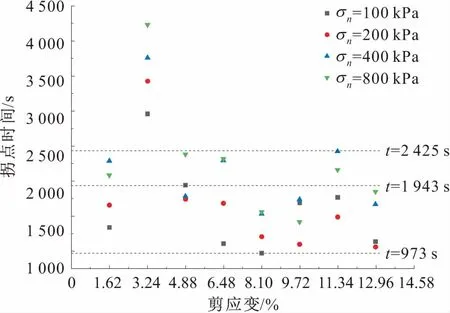
图11 不同垂直压力和剪应变下滑带土应力松弛双指数衰减模型拟合曲线的拐点(T点)时间分布图Fig.11 The distribution diagram of turning point of the fitting curve of the double exponential decay model of the stress relaxation of sliding zone soil with different vertical pressure and shear strain

由图11可见，除了剪应变为3.24%以外，其他剪应变条件下滑带土应力松弛双指数衰减模型拟合曲线拐点T(两个松弛阶段的分隔时间点)所对应的时间均分布在973～2 425 s内，且与垂直压力存在一定的关系：低垂直压力(100 kPa、200 kPa)时拐点(T点)均分布在1 943 s以下;高垂直压力(400 kPa、800 kPa)时(T点)多分布在1 943 s以上。其实，该拟合曲线拐点T的时间分布与滑带土的应力-应变曲线密切相关(见图3)，当应变为3.24%时滑带土的剪切应力接近峰值强度，所以其弹塑性达到最大，导致出现黏塑性的时间延长。

第I、第II松弛阶段滑带土应力松弛量的占比分布图，见图12。

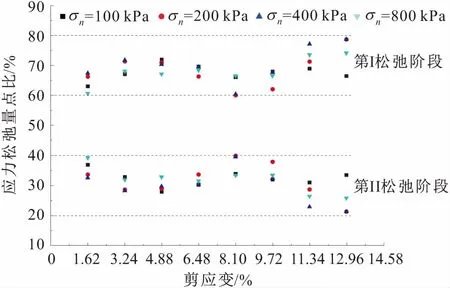
图12 第I、II松弛阶段滑带土应力松弛量的占比分布图Fig.12 The distribution diagram of the stress relaxation amount proportion of relaxation stage I and II of sliding zone soil

由12可见：第I松弛阶段内滑带土的应力松弛量占总松弛量的60%～80%；第II松弛阶段内滑带土的应力松弛量占总松弛量的20%～40%；第I松弛阶段与第II松弛阶段内滑带土的应力松弛量呈对称的关系，且第I松弛阶段滑带土应力松弛量的大小决定了总应力松弛量的大小和分布。

为了研究剪应变增量大小对滑带土应力松弛特征的影响，开展了剪应变增量为Δγ2=3.24%的滑带土应力松弛试验。以垂直压力为800 kPa为例，分别绘制剪应变增量分别为Δγ1=1.62%和Δγ2=3.24%时滑带土应力松弛双指数衰减模型拟合曲线拐点(T点)时间与剪应变的关系曲线以及滑带土第I、第II松弛阶段应力松弛量占比与剪应变的关系曲线，见图13和图14。

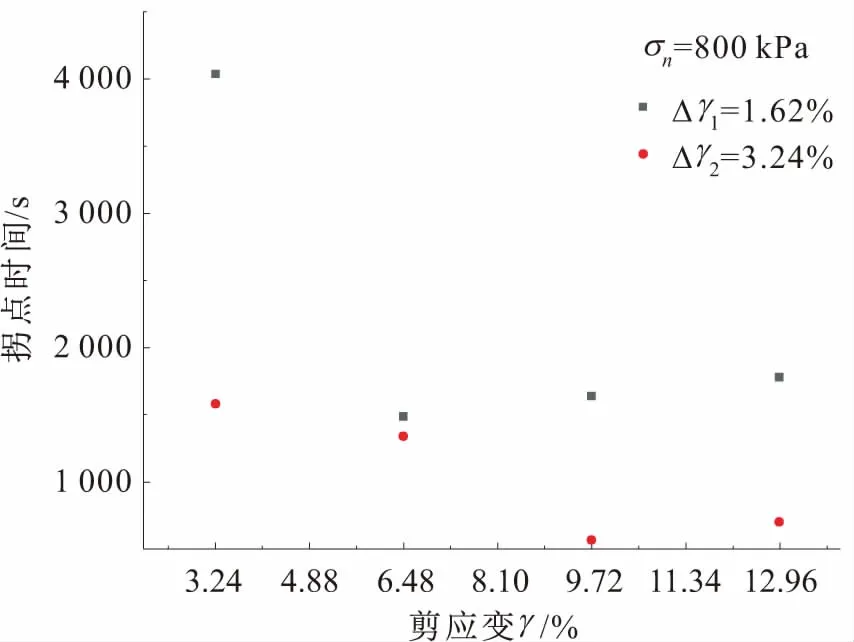
图13 不同剪应变增量下滑带土应力松弛拟合曲线拐点 (T点)出现的时间与剪应变的关系曲线 (σn=800 kPa)Fig.13 The relationship between turning point time of the fitting curve of stress relaxation of sliding zone soil and shear strain with different shear strain increments based on double exponential decay model

图14 不同剪应变增量下滑带土第I、第II松弛阶段应力松弛量占比与剪应变的关系曲线(σn=800 kPa)Fig.14 The relationship between the stress relaxation amount proportion of relaxation stage proportion of sliding zone soil and shear strain of relaxation stage I and II with different shear strain increments(σn=800 kPa)

由图13和图14可见，剪应变增量越小，滑带土应力松弛双指数衰减模型拟合曲线拐点T的时间越大，第I松弛阶段滑带土应力松弛量的占比也越大，这与应力松弛时间、土样排水固结密切相关；当剪应变增量增加一倍时，达到相同应变(如14.58%)所需的时间减小了一半。