某型发动机压气机叶-盘结构优化分析

魏武国， 彭伟程

(中国民用航空飞行学院航空工程学院， 德阳 618307)

在保证结构可靠性的前提下，提高航空发动机推重比有两个途径：一是保持发动机重量不变的情况下提高推力；二是保持推力不变的情况下减轻发动机重量。在发动机转子部件上采用整体叶盘(blisk)结构是一种有效的减重方法。20世纪60年代初，一些小型、短寿命发动机上就已经出现了整体叶盘结构；随后，逐步推广应用到小型涡轴、涡桨、大型军用涡扇发动机上；21世纪初，开始在高涵道比民用涡扇发动机上应用[1]。

在整体叶盘应用范围逐步扩大的过程中，制约其应用的两个工程问题有了深厚积累：一是以电化学加工、精密焊接、精密铸造等为代表的整体叶盘制造工艺有了长足进步[2-5]；二是整体叶盘的维修性变好，即外缘叶片在修理限度以内的损伤，可利用在翼孔探打磨技术进行修理。因此，在不改变外缘叶片气动外形、盘鼓连接半径、盘鼓连接螺栓、鼓筒轴向长度的条件下，将现有型号发动机榫头-榫槽连接式叶盘结构改为整体叶盘结构、就成了一种能快速提高后续批次发动机推重比的途径，但需对叶盘结构上至少两处位置进行改型优化：①叶片与轮盘的连接处。将叶根榫头与盘缘榫槽的间隙配合优化为叶身和盘缘直接连接；②第一步优化后，叶盘外缘质量减轻，轮盘子午面形状可进一步优化。

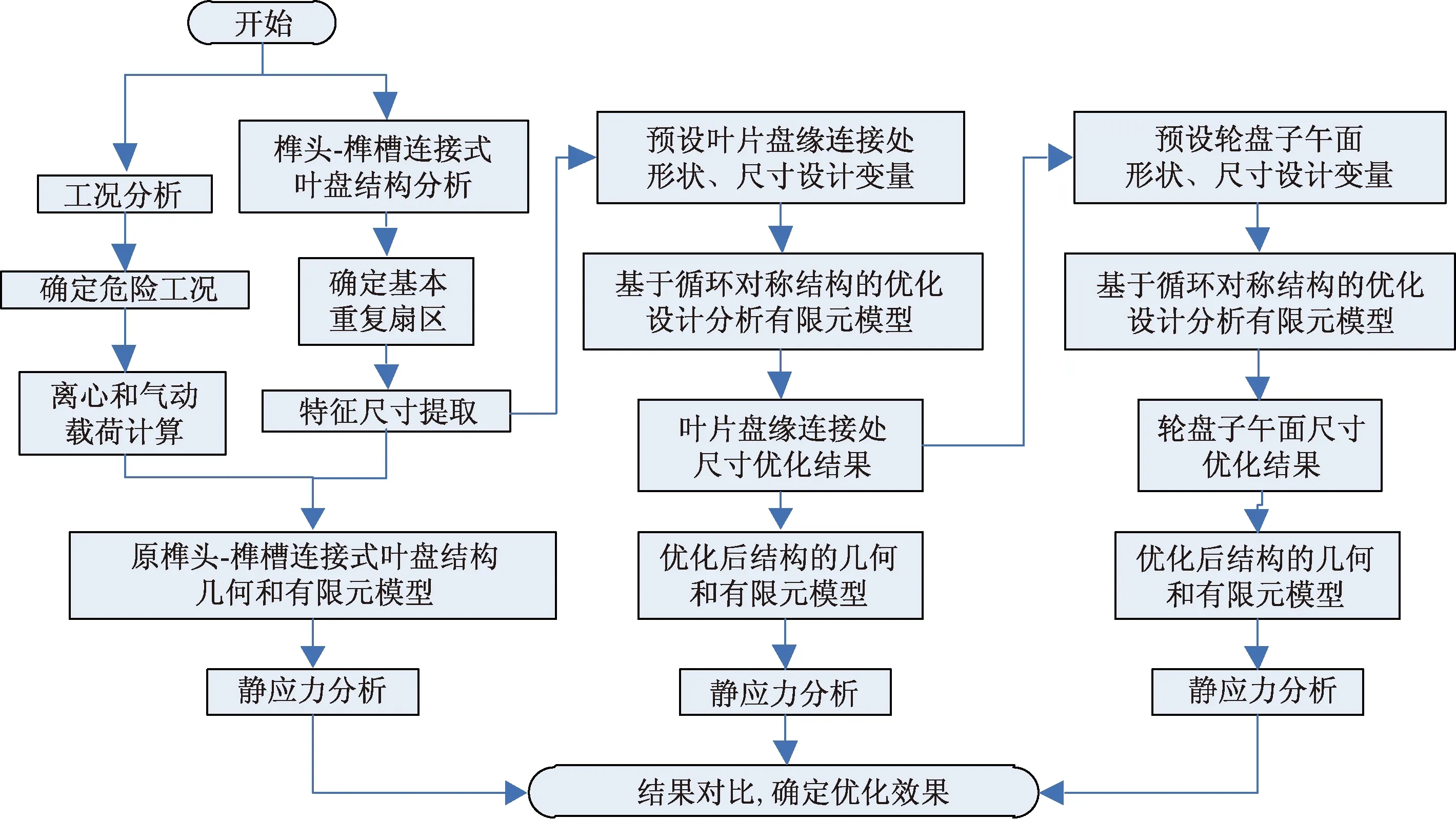
图1 榫头-榫槽连接式叶盘结构优化流程Fig.1 Optimization process of root-groove joint type blade-disc structure

国内学者对航空发动机盘类零件优化设计工作已逐渐深入，一些学者试图建立不预设结构形状的正向优化设计方法：刘超[6]提出了基于随机抽样敏度分析的双向渐进结构优化方法(bi-directional evolutionary structural optimization with random sampling sensitivity analysis, RSSA-BESO)，应用于涡轮盘拓扑优化中，比同等条件下单辐板盘减轻30.42%；文献[7-8]在RSSA-BESO基础上，提出了基于自适应策略的随机抽样敏度分析的双向渐进结构优化方法(self-adaption-bi-directional evolutionary structural optimization with random sampling sensitivity analysis, A-RSSA-BESO)，应用于风扇盘拓扑优化中，得到三辐板、四辐板风扇盘结构比单辐板盘分别减轻17.1%、19.42%；刘小刚等[9]在ANSYS优化平台上，运用基于固体各向同性材料惩罚模型(solid isotropic material with penalization, SIMP)函数的变密度法、通过扩大求解域对某发动机风扇结构开展拓扑优化分析，取得良好效果。而另一些学者则对盘类零件的原结构或预设结构形状直接开展尺寸优化，试图进一步减重：李伦未等[10]和陆山等[11]基于ANSYS优化平台，对单辐板、多辐板风扇盘结构、整体叶盘结构进行尺寸优化设计，证明了多辐板风扇盘、整体叶盘的结构优越性；张大义等[12]预设C型和M型两种高负荷斜流压气机叶盘结构方案，进行尺寸优化设计，证明M型方案减重更优。但目前还没有见到从现役机型榫头-榫槽连接式叶盘结构出发，综合考虑离心、气动载荷并尽量不改变鼓筒、连接螺栓等邻近零件几何参数的强约束条件下的结构优化工作。

在盘类和非盘类零件的结构优化[13-14]工作中，都证明了ANSYS软件平台结构优化设计与计算的可靠性。因此，在分析航空发动机转子结构特点的基础上，现以叶片-轮盘-鼓筒为改型优化对象，合理预设叶-盘连接处、轮盘子午面形状和尺寸设计变量；基于循环对称结构静应力分析方法，在ANSYS软件优化设计模块中采用一阶方法进行尺寸优化分析，计入叶、盘、鼓在最大转速工况下的离心和气动载荷，考虑叶片离心力弯矩补偿气体力弯矩从而改善盘缘应力状态的效应，由此建立从榫头-榫槽连接式叶盘结构到整体叶盘结构的优化策略与方法。

1 叶-盘结构改型优化分析方法

发动机转子由基本结构单元、即叶-盘-鼓轴向连接成多级组成，但每一级叶-盘结构都具有旋转周期对称性。因此，在通用有限元软件平台上、基于循环对称结构静应力分析方法，建立从榫头-榫槽连接式叶盘结构到整体叶盘结构的优化策略与方法，如图1所示。

分析实际发动机上榫头-榫槽连接式叶盘结构特点，确定循环对称结构基本重复扇区，提取特征尺寸，在通用有限元软件中建立扇区的三维实体模型；同时分析叶盘结构的工作条件，计算其在最大起飞工作状态下承受的离心、气动载荷；建立叶盘结构静应力分析的三维有限元模型。

确定叶盘结构优化的目标函数和约束条件，合理预设叶身与盘缘直接连接处的形状、尺寸设计变量，进行优化计算，将榫头-榫槽连接式叶盘结构优化为整体叶盘结构；用同样方法对轮盘子午面进行尺寸优化，得到轻量化后的整体叶盘结构。最后对比分析优化前、后的结构，确定减重效果。

结构优化的目的是减重，在材料密度为常数的情况下，可将目标函数设为结构体积。因此叶盘结构优化的本质是：在满足使结构可靠的应力约束条件下，于尺寸设计变量取值范围内，找出一组使叶盘结构体积最小的尺寸设计变量确定值，即

minV=f(X1,X2,…,Xn)

(1)

(2)

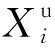
2 算例计算

2.1 分析对象

图2是某型发动机9级高压压气机子午面截图，各级叶盘均采用了榫头-榫槽连接式结构。不失一般性，选取第三级叶盘结构为优化分析对象，根据前述流程和方法，分两步对该结构进行优化减重分析，即在不改变叶片气动外形、盘鼓连接半径、盘鼓连接螺栓、鼓筒轴向长度的情况下，首先对叶盘连接处进行优化，再对轮盘子午面形状进行优化。

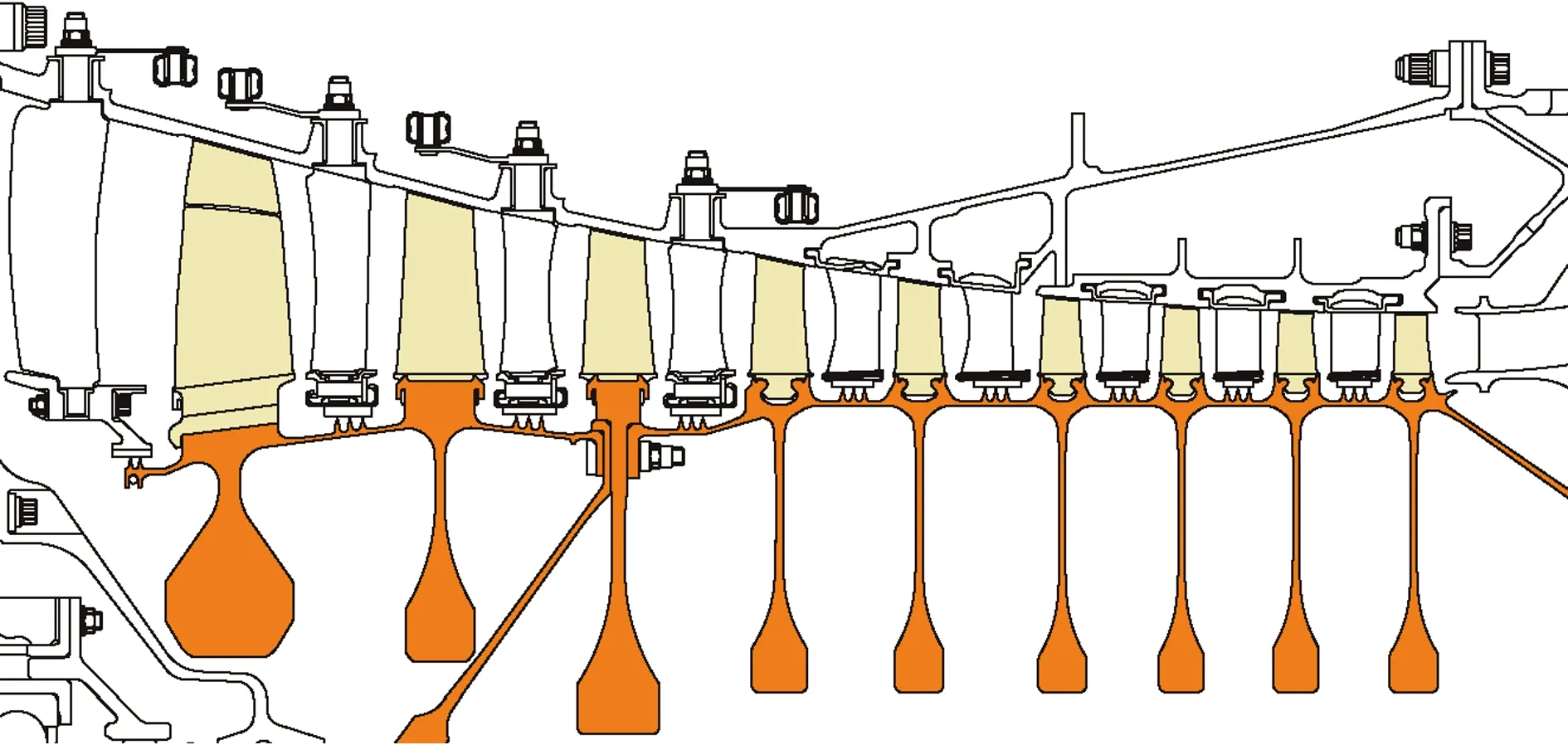
图2 某型发动机榫头-榫槽连接式压气机叶盘转子Fig.2 Root-groove joint type compressor blade-disc rotor of a turbofan engine

(1)叶盘连接处。在图3原结构的基础上、不修改叶根旋转半径，对叶盘连接处进行重修设计，如图4所示，取消了原结构中叶根榫头与盘缘榫槽的间隙配合，并取X1、X2、X3为尺寸设计变量，X1、X2、X3都是从旋转中心计起的半径。根据原结构设计尺寸，确定X1、X2、X3的取值范围，列于表1中；另外，为保证优化计算时3个尺寸设计变量之间的正确关系，可令X1≤X2-4 mm,X2≤X3。

(2)轮盘子午面形状。第(1)步优化后，对轮盘子午面形状进行重新设计，如图5所示。新结构的轮盘由内缘等厚空心盘、过渡段、外缘等厚盘和盘缘等几部分组成，其中内缘等厚空心盘与过渡段的形状尺寸包含在原轮盘子午面形状之内。取X4、X5、X6为尺寸设计变量，X4是内缘等厚盘厚度的1/2，X5是内缘等厚盘在径向的长度，X6是内、外缘等厚盘过渡段在子午面视图上的半径。同样根据原结构设计尺寸，确定X4、X5、X6的取值范围列于表1中，且限定3个尺寸设计变量之间的关系为X4-4.1 mm≤X6，式中4.1 mm是外缘等厚盘厚度的1/2。

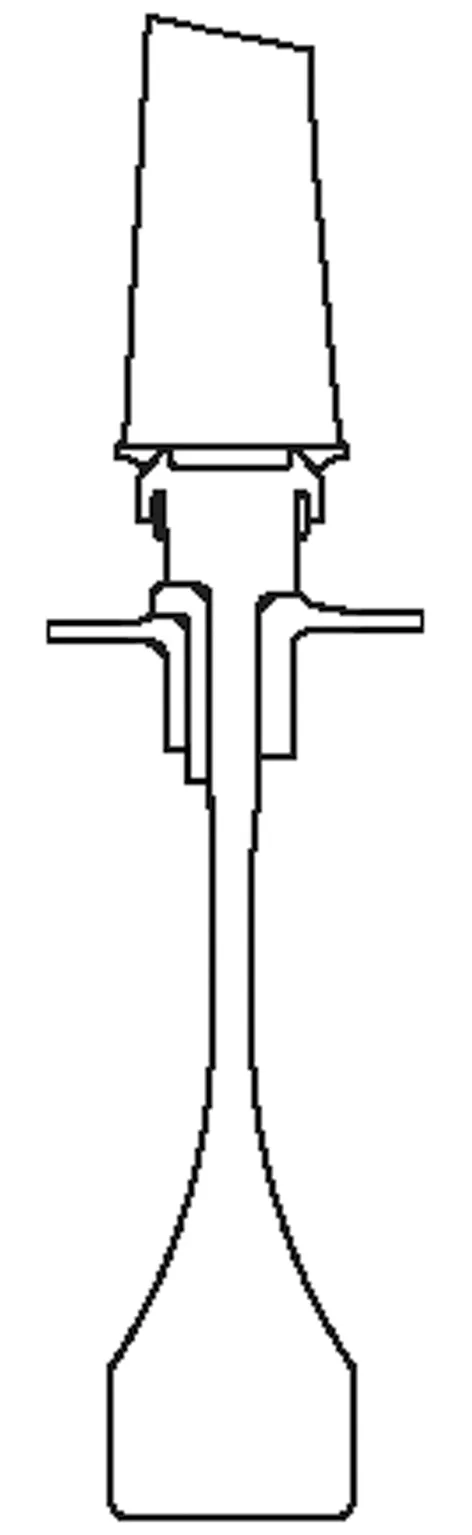
图3 原榫头-榫槽连接式叶盘结构Fig.3 Root-groove joint type blade-disc structure

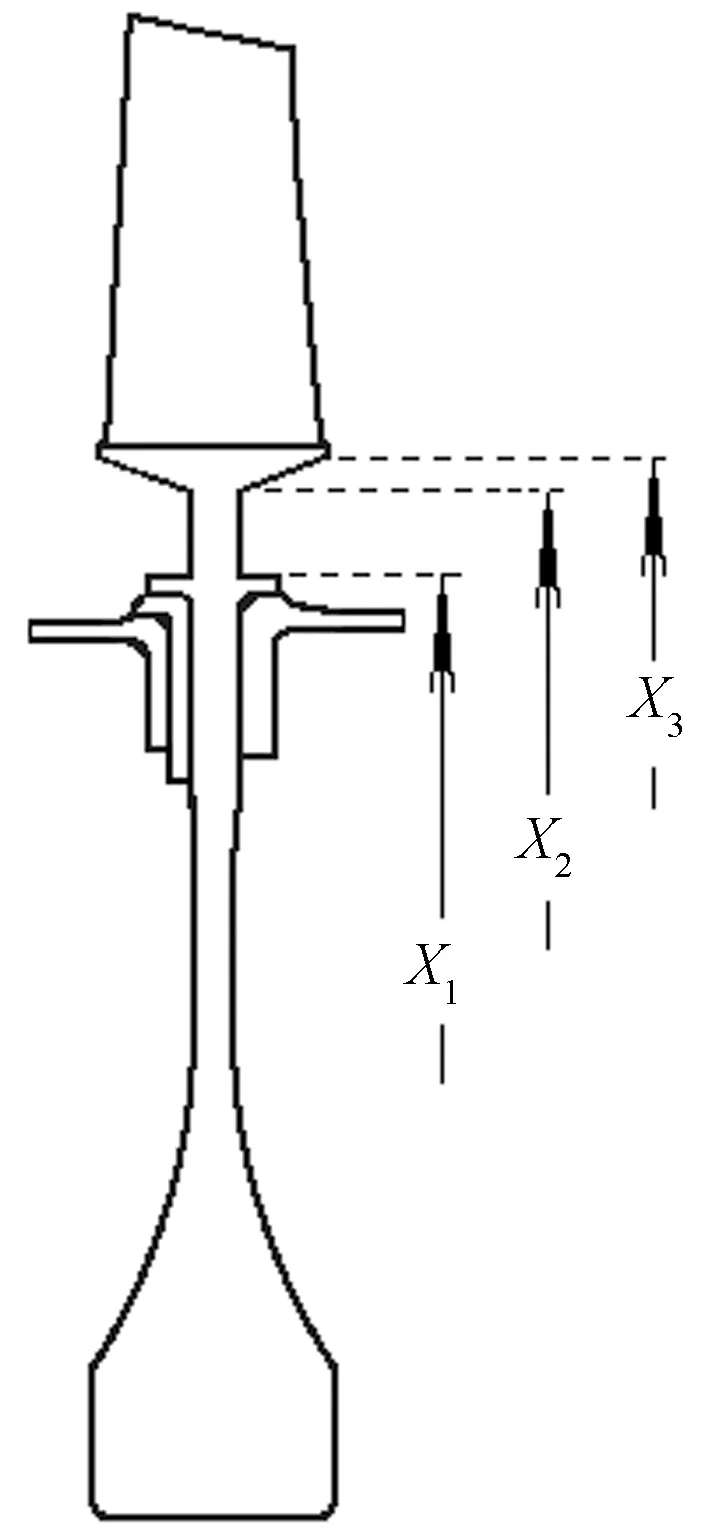
图4 叶盘连接处的优化设计变量Fig.4 Optimal design variables at the connection position of blade and disc rim

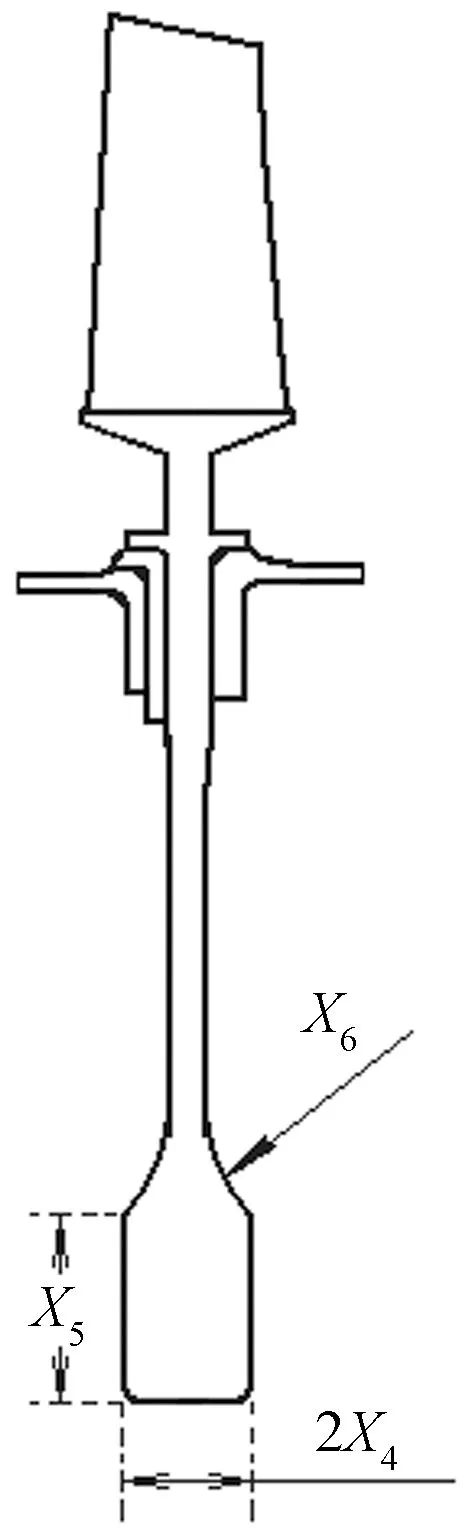
图5 轮盘子午面的优化设计变量Fig.5 Optimal design variables of disc

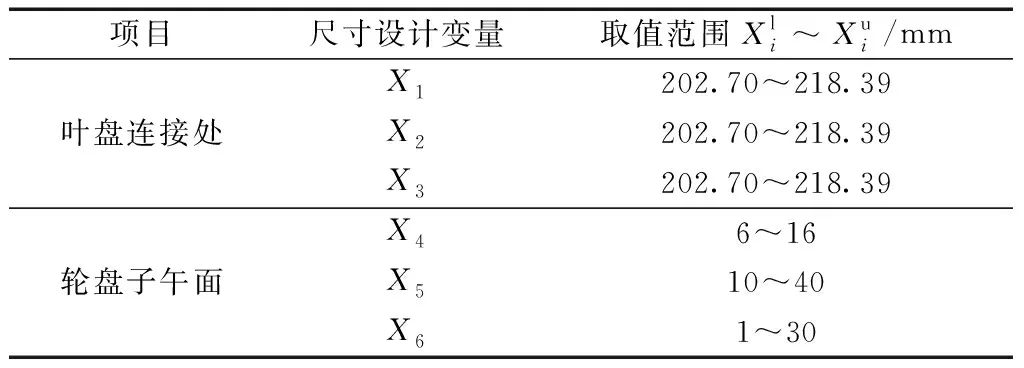
表1 尺寸设计变量的取值范围Table 1 The value range of dimensional design variables

2.2 工况及载荷计算

压气机叶盘结构整体要承受旋转工作时的离心载荷，此外，外缘叶片还要承受气体力载荷。对于压气机转子叶片而言，通常以叶根截面作为离心力弯矩补偿气体力弯矩的对象，从而改善叶根截面应力状态。对于整体叶盘结构，叶根截面就是叶盘连接处，为使叶盘连接处的应力状态和优化更精准，需要同时计入离心和气体力载荷。

选取压气机的最大起飞工作状态，转速ω=1 514.25 rad/s，此时该级转子叶片的进出口气流参数均值如表2所示，可用式(3)和式(4)计算叶片承受的轴向和切向气体力大小。

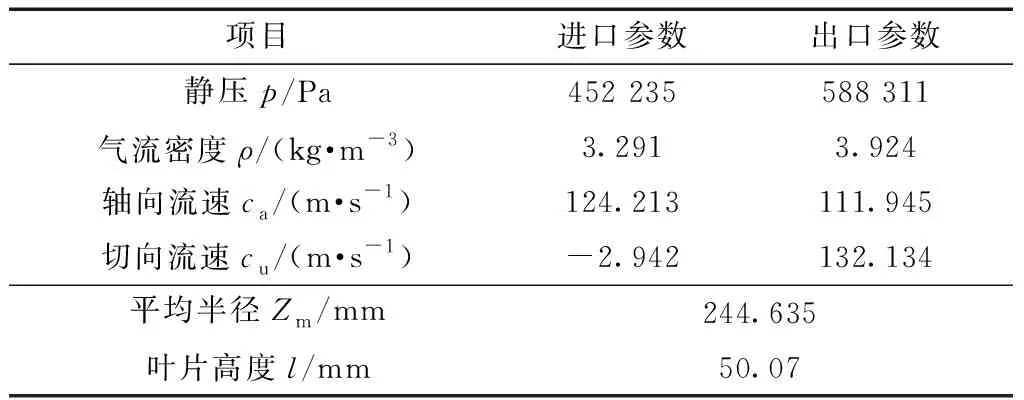
表2 最大起飞工作状态下转子叶片进出口气流参数Table 2 Airflow parameters at inlet and outlet of rotor blade under maximum take-off working condition

根据动量定理和作用力与反作用力定律，单位叶高上受到的轴向气体力[15]计算公式为

(3)

切向气体力[15]计算公式为

(4)

式中：p1m、p2m分别为叶片进、出口截面平均半径处气流静压；ρ1m、ρ2m分别为叶片进、出口截面平均半径处气流密度；c1am、c2am分别为叶片进、出口截面平均半径处气流轴向流速；c1um、c2um分别为叶片进、出口截面平均半径处气流切向流速；Zm为转子叶片的平均半径(即叶根与叶尖半径的平均值)；Q为叶片数目，本文中Q=60。

计算出该级压气机转子叶片承受的轴向气体力大小为172.49 N，施加在叶盆面上，沿轴向指向叶背；切向气体力大小为75.99 N，施加在叶盆面上，沿切向指向叶背。

2.3 有限元模型的建立

以工作时的旋转轴线为对称轴，叶盘结构呈现旋转周期对称性。为节省计算资源，在有限元结构分析中采用循环对称结构分析方法。取夹角为 6° 的扇形结构(1/60)为基本重复扇区，依图3形状和设计尺寸，忽略榫槽前后表面的卡环槽等一些对计算结果影响不大的细小结构，基于通用有限元软件平台建立原榫头-榫槽连接式叶盘结构静应力分析的三维有限元模型。

同理，依图4形状和设计尺寸建立叶盘连接处优化分析的有限元模型，经优化分析确定尺寸设计变量X1、X2、X3后，再依图5形状和设计尺寸建立轮盘子午面优化分析的有限元模型，优化分析确定尺寸设计变量X4、X5、X6。待尺寸设计变量X1～X6确定后，再依图4和图5建立叶盘连接处优化后的、轮盘子午面形状优化后的叶盘结构静应力分析有限元模型。

本文研究中，连接前后级叶盘的鼓筒是半径较大的薄壁零件，工作转速下鼓筒的径向位移大于轮盘上同半径位置处的径向位移，即轮盘会承受部分鼓筒的离心载荷，因此，在对叶盘结构进行静应力分析时，不能忽略鼓筒，有限元模型中轮盘前后表面各保留了部分鼓筒结构。

统一取叶、盘、鼓的材料为钛合金TC11，结构的工作温度在200 ℃左右，将此温度下的材料常数[16]列于表3中。其中屈服强度σs是TC11盘模锻件200 ℃时σ0.2的-3σ值。

表3 压气机叶、盘、鼓的材料常数Table 3 Material properties of compressor blade, disc and drums

实际结构上，叶根榫头与盘缘榫槽是间隙配合，但在最大转速工况下，叶片离心力使接触面紧压在一起，可视为固定连接。此外，由于轮盘与鼓筒的连接有定心要求，因此盘缘内圆柱面与鼓筒外圆柱面之间采用紧配合、再用精密螺栓连接的方式。本例静应力和优化分析的有限元模型中，将叶根榫头与盘缘榫槽的连接、盘缘内圆柱面与鼓筒外圆柱面的连接接触设定为绑定接触。根据设定，绑定接触的两个接触面间没有相对滑动和分离，可以将接触区域看作是被连接在一起的；因为接触面积是保持不变的，所以这种接触可用于线性求解。在优化迭代过程中的静应力求解计算中和三种结构静应力对比分析求解计算中，既贴合最大转速工况下叶-盘-鼓结构的连接接触实际，又没有忽略上述两个接触位置的真实应力状态。

划分网格前，设置好周期扩展参数，方便重复扇区上下界面上的节点进行匹配。划分网格时，三维实体模型中可扫掠部分均采用高阶六面体单元，其余非扫掠部分、比如叶根缘板等采用高阶四面体单元；绑定接触对中的接触面采用高阶四边形单元Conta 174、目标面采用Targe 170单元。

本文研究中所有叶盘结构的边界条件均设置为：盘鼓连接的精密螺栓孔内壁面径向自由、切向和轴向固定的约束，贴近转子工作实际，由此建立起了叶盘结构静应力仿真分析、优化仿真分析的三维有限元模型。图6～图8为对应图3～图5叶盘结构的基本重复扇区的网格划分，原榫头-榫槽连接式叶盘结构的重复扇区划得22 076 个节点、5 188个单元。

3 结果分析

3.1 尺寸优化计算

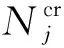
通用有限元软件ANSYS的优化设计模块中有两种优化方法：零阶方法和一阶方法。一阶方法基于设计灵敏度，先计算相关变量的梯度以确定搜索方向，再通过对目标函数添加罚函数将约束优化问题转化为无约束优化问题，进而采用线性搜索来寻优，适合于精细的优化分析[17]。根据本文提出的叶盘结构优化流程，本例采用一阶方法进行优化计算，设置好迭代次数后自动进入搜索循环，找到满足约束条件的解，如表5所示。

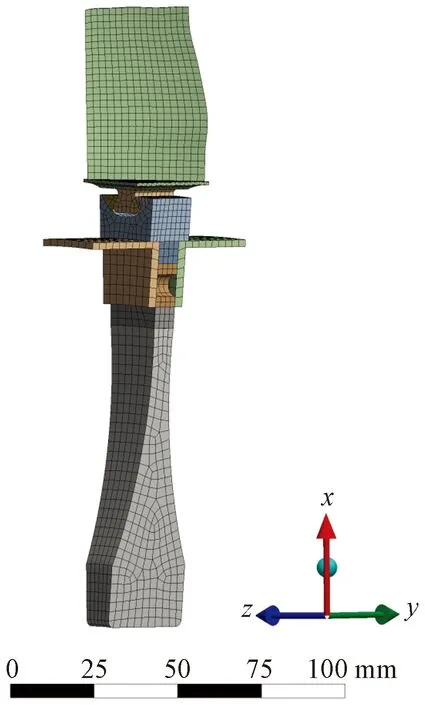
图6 原榫头-榫槽连接式叶盘结构的重复扇区网格划分Fig.6 Meshing of root-groove joint type blade-disc structure’s repeated sector

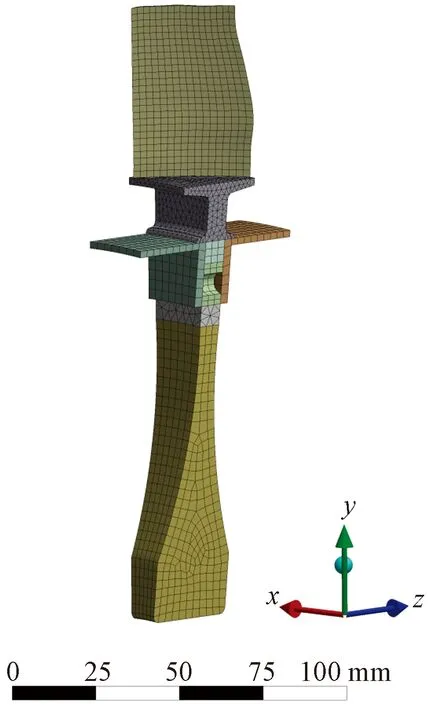
图7 叶盘连接处优化分析用的叶盘结构重复扇区网格划分Fig.7 Meshing of blisk’s repeated sector used for optimization analysis of blade disk connection

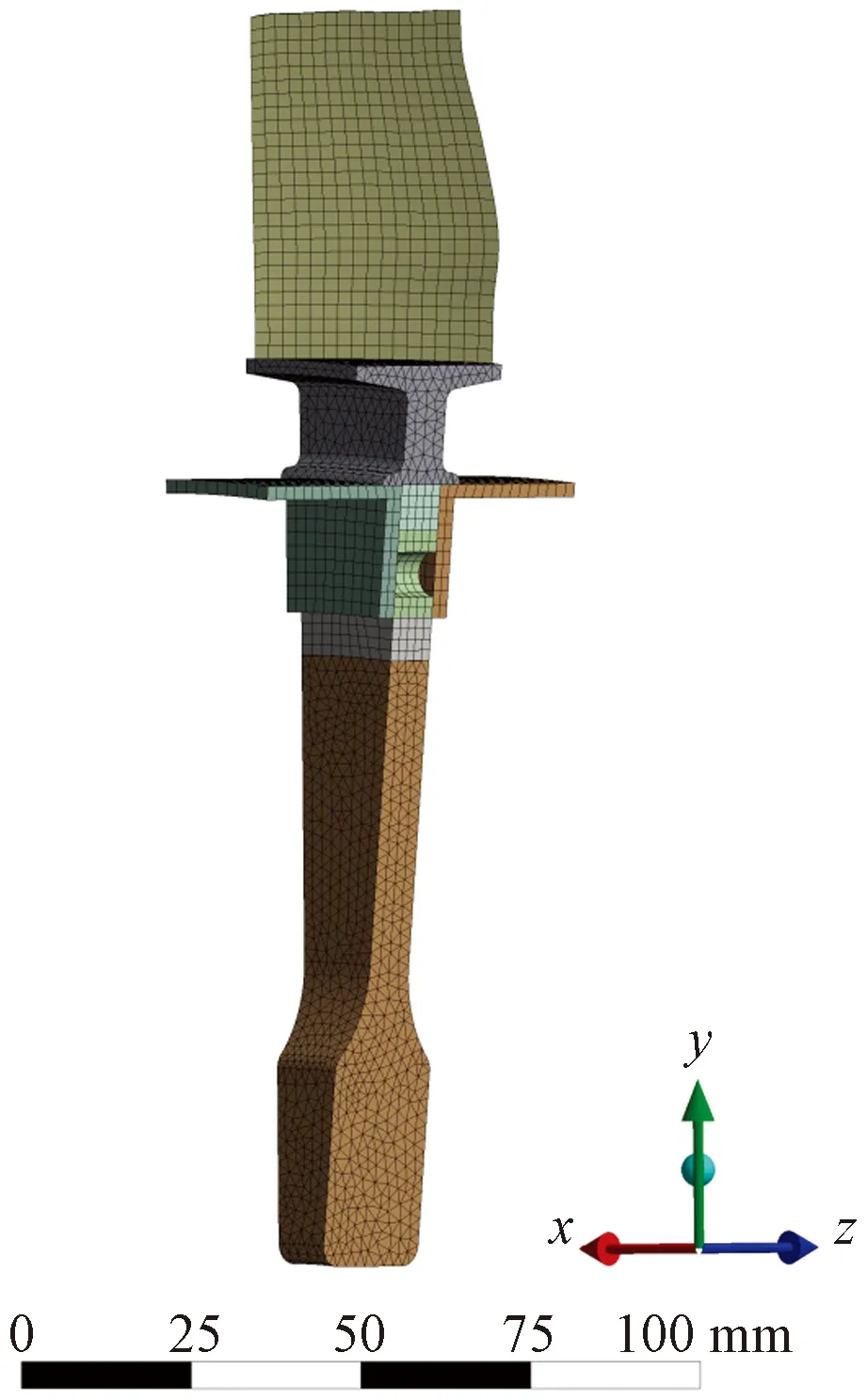
图8 盘身优化分析用的叶盘结构重复扇区网格划分Fig.8 Meshing of blisk’s repeated sector used for optimization analysis of disc body

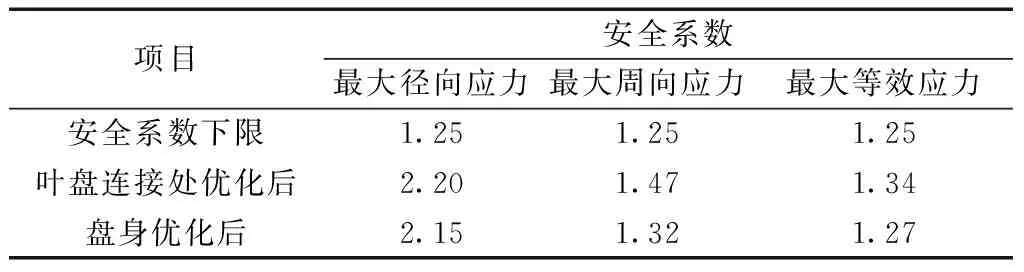
表4 优化迭代时的应力约束条件Table 4 Stress constraint conditions during optimization iteration

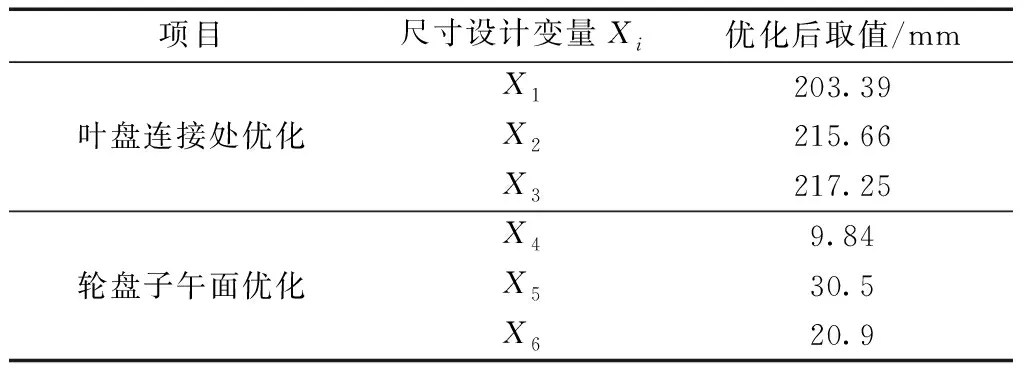
表5 尺寸设计变量的优化结果Table 5 Optimization results of dimensional design variables

3.2 三种结构应力分布对比

将尺寸设计变量取为表5中优化后的值，在通用有限元软件平台中建立优化后的、最大转速工况下静应力分析的整体叶盘的三维有限元模型，盘鼓接触对设置、网格划分、边界条件等，同前述优化分析的叶盘结构模型。

分别在原榫头-榫槽连接式叶盘结构上、叶盘连接处优化后的结构上、盘身优化后的结构上施加相同的离心和气动载荷，计算静应力分布，其中径向、周向、等效应力的最大值和平均值，叶尖处径向位移等计算结果如表6所示。

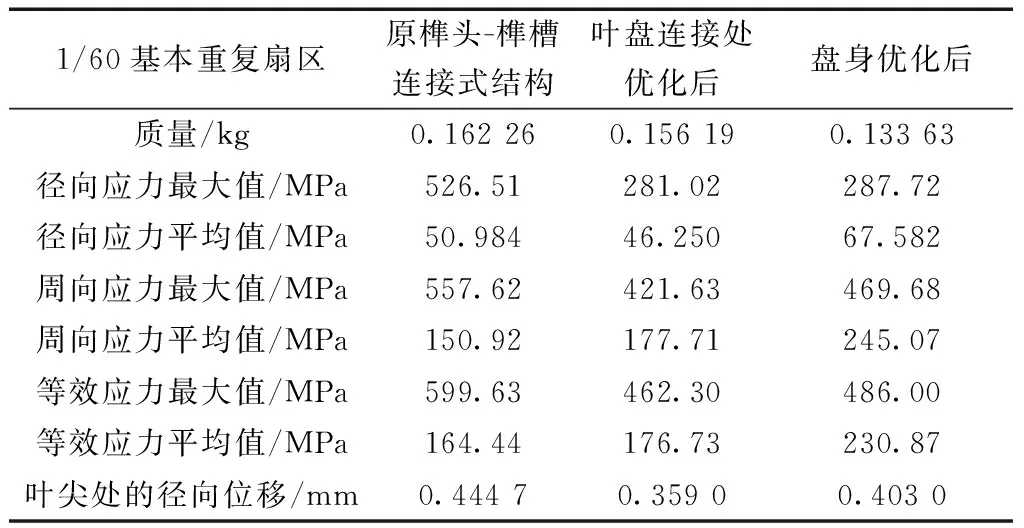
表6 叶盘结构优化前后对比Table 6 Comparison of blade-disc structure before and after optimization

图9～图11分别是三种叶盘结构在最大转速工况下的径向应力分布对比、周向应力分布对比、等效应力(von-Mises)分布对比。为方便同时查看结构表面和盘身内的应力分布，在设置应力计算结果显示时，沿某半径将叶盘结构的应力云图切开，同时利用应力探针显示了一些特殊点的应力值大小，如图9～图11所示。

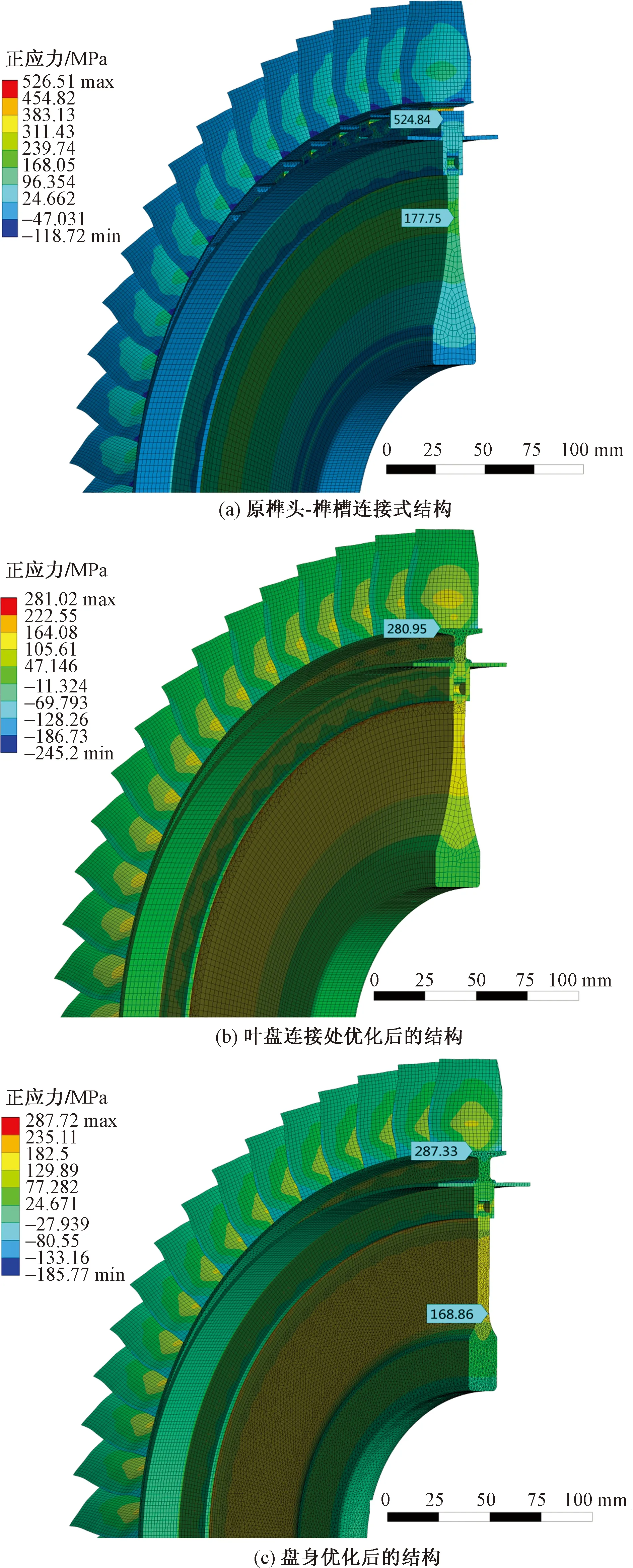
图9 径向应力分布对比Fig.9 Comparison of the radial stress distribution

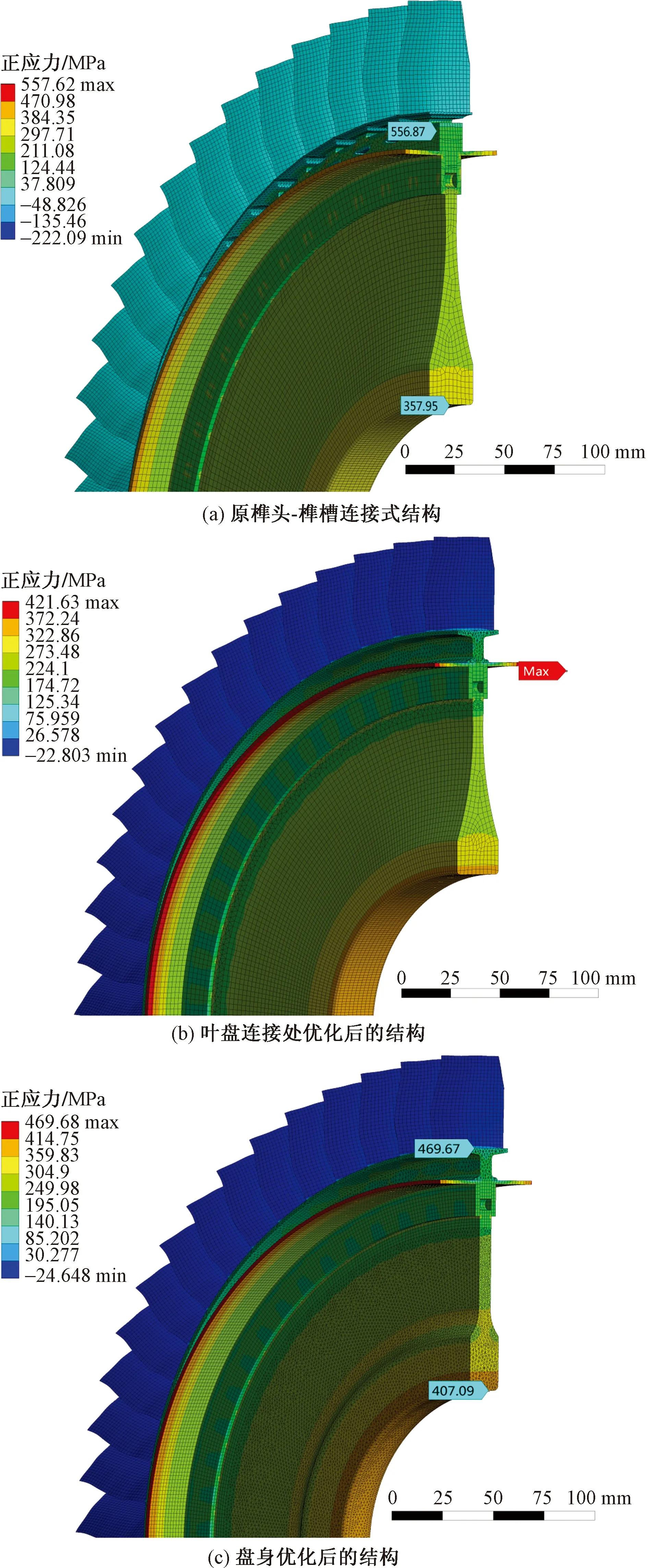
图10 周向应力分布对比Fig.10 Comparison of circumferential stress distributions

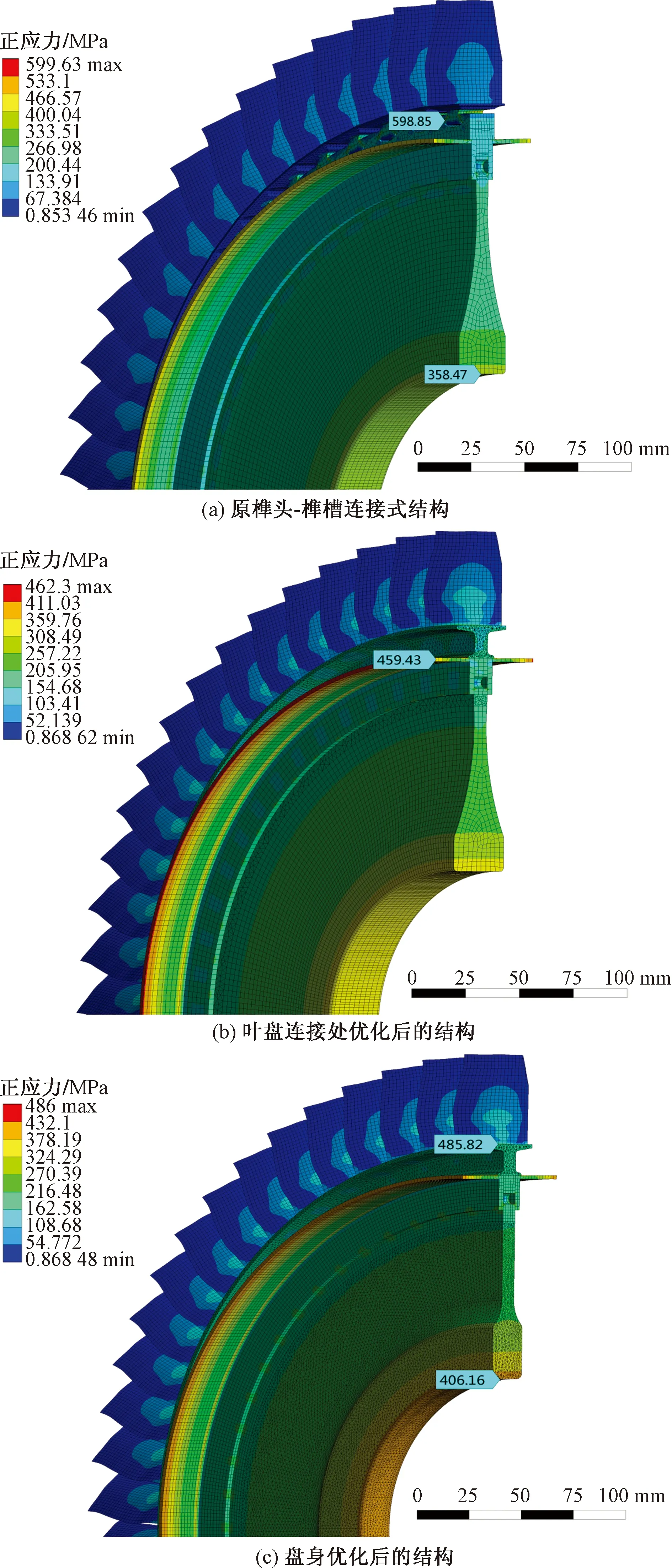
图11 等效应力分布对比Fig.11 Comparison of equivalent (von-Mises) stress distributions

结合表6分析发现：完成优化后的结构减重17.64%，径向、周向、等效应力最大值分别减小了45.35%、15.77%、18.95%，径向、周向、等效应力平均值分别增加了32.56%、62.38%、40.40%，结构整体的应力分布更加合理，且转子叶片叶尖的径向位移变化小于10%，取得较好减重效果。

4 结论

针对发动机转子叶-盘-鼓基本结构单元，提出了从榫头-榫槽连接式叶盘结构到整体叶盘结构的两步优化方法，应用于某发动机高压压气机第三级叶盘结构优化中，取得较好减重效果。

(1)在不改变叶片气动外形、盘鼓连接半径等强约束条件下，合理预设需优化位置的形状和尺寸设计变量，尽量不影响发动机整机气动性能。

(2)基于循环对称结构静应力分析方法，缩减了优化迭代中、静应力计算的有限元模型的规模，提高了计算效率。

(3)在静应力计算的有限元模型中，设置贴合实际的叶-盘-鼓间的接触，既可线性求解，又能计入接触面上的真实应力状态。

(4)选取最大转速工况为优化设计点，计入鼓筒载荷的同时，还计入了叶片离心力弯矩补偿气体力弯矩从而改善盘缘应力状态的效应，贴合承载实际。