浅谈齿距差异对榫齿载荷分配的影响
2022-01-08陈剑康剑雄
陈剑 康剑雄
(1.中国航发湖南动力机械研究所,湖南株洲 412002;2.中小型航空发动机叶轮机械湖南省重点实验室,湖南株洲 412002)
0.引言
枞树形榫头是当前航空发动机叶片与轮盘之间普遍采用的连接结构形式。通常,枞树形榫头包含两对以上的榫齿,各榫齿之间的载荷分配是否均匀对榫接的应力集中和寿命有重要影响[1-2]。在绝大多数发动机型号中,榫头/榫槽均为等齿距设计,即在不考虑齿距公差的条件下,各对榫齿理论上是同时接触的。若将榫头和榫槽设计为不同齿距,则会改变各对榫齿接触的先后顺序,导致载荷分配依次向先发生接触的榫齿倾斜。杨晓洁[3]针对两齿榫头开展了第一对榫齿单侧出现不同间隙时的数值模拟,其结果表明:随着间隙的增大,第一对齿的载荷减轻,第二对齿的载荷加重;榫接的最大应力先减小后增加,并且呈线性关系。王少飞[4]等人研究了三齿榫头齿距小于榫槽齿距导致第三齿接触,一、二齿出现间隙时最大接触应力随间隙大小的变化规律,发现随着榫头/榫槽配合间隙的增加,接触应力呈增大的趋势,同时最大应力点在不同的齿间转移。
本文针对一般性的榫接结构,采用力学分析模型,通过将离心载荷与温度场进行分离,着重研究齿距差异与榫头刚度之间的相互作用,系统性地分析齿距差异对榫齿载荷分配的影响规律。
1.分析模型
1.1 受力分析
在发动机真实工作环境中,榫接的受力包括离心力、气动力、振动力以及自身的热应力。这些载荷当中,离心力居于主导地位。对叶片榫头而言,伸根及其以上结构产生的离心力是外拉伸载荷(简称外离心力),叠加自身的离心力之后(合称叶片离心力)以榫齿接触力的形式传递给轮盘榫头。轮盘榫头承受叶片离心力,叠加自身的离心力之后(合称总离心力)传递给轮盘。若以叶片榫头和轮盘榫头作为控制体,按照力的叠加原理,将榫齿之间的接触力与榫头自身的离心力相分离,其结果如图1所示。可以看出,榫齿之间的接触力对叶片榫头和轮盘榫头的作用效果相同,其合力均等于叶片离心力;而榫头自身离心力的作用效果有所区别,叶片榫头的离心力使叶片榫头产生压应力,轮盘榫头的离心力使轮盘榫头产生拉应力。
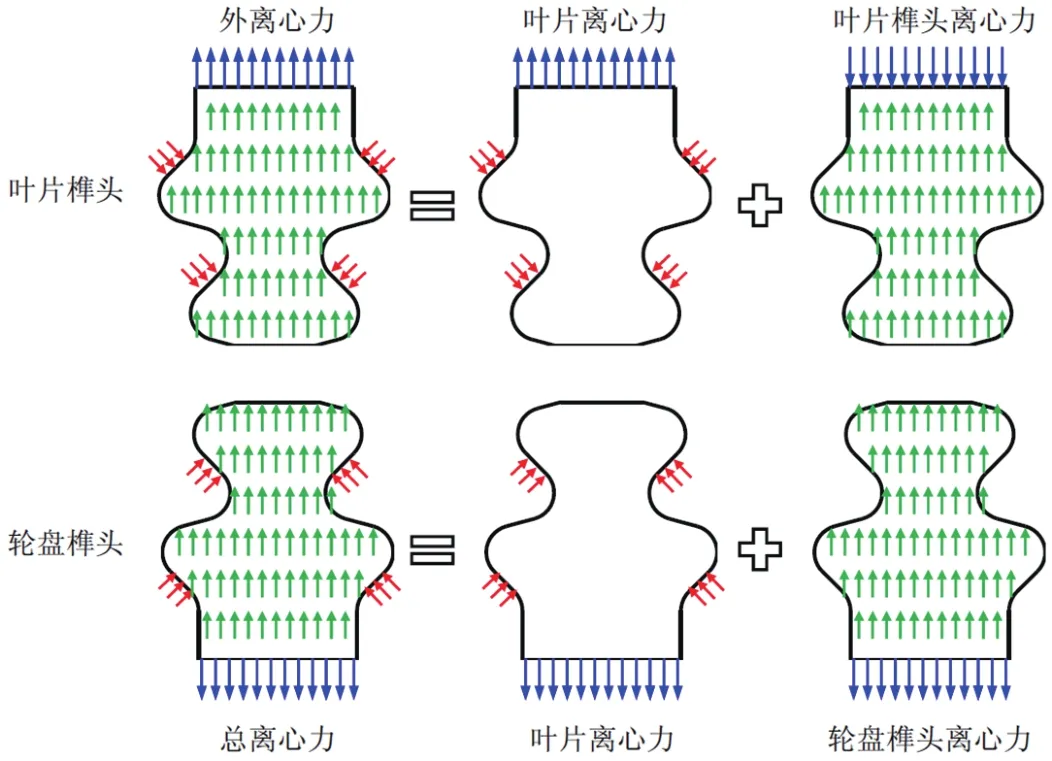
图1 受力分析
1.2 等效刚度模型
通过受力分析,榫头上的作用力可以分为两大类:一类为拉伸力和接触力这样的面载荷,在构建力学分析模型时可以按集中力对待(如图2所示,f为叶片离心力,f1和f2分别为第一对榫齿和第二对榫齿接触力的合力,且满足关系式f=f1+f2);另一类为榫头自身离心力fb这样的体载荷。无论是哪一类载荷,都与转速的平方成正比。当转速为ω时,f产生的齿距变形量为Δt1=aω2;fb产生的齿距变形量为Δt2=bω2。如果将Δt视作均由f产生,对叶片榫头而言等效刚度为k1=f/Δt=m/(a+b);对轮盘榫头而言等效刚度k2=f/Δt=m/(a-b),k1、k2均为常数。考虑到榫头离心力相对叶片离心力而言是小量,这种近似不会对力学特征带来本质性影响。根据该力学模型,有f1=k2Δt,f2=k1Δt,即
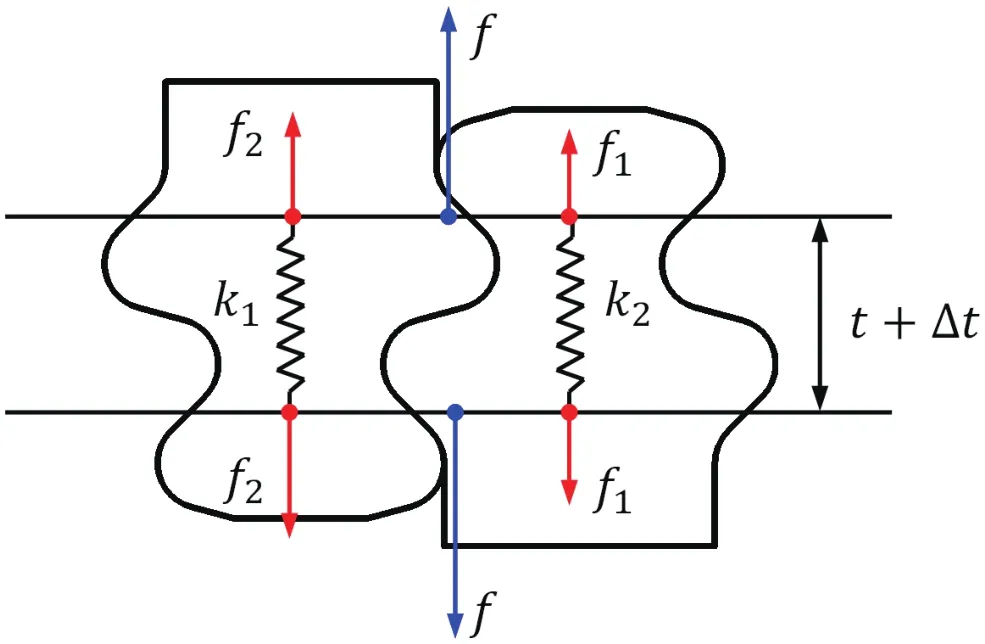
图2 等效刚度模型

该公式清楚地表明,各榫齿之间的载荷分配本质上是由叶片榫头与轮盘榫头的刚度匹配关系决定的。也就是说,只要刚度匹配合理,榫头/榫槽完全可以采用等齿距设计。
2.齿距差异影响分析
2.1 两齿榫头
若榫头/榫槽为等齿距设计,即k1=k2时,第一对榫齿的接触力f1与第二对榫齿的接触力f2时刻保持相等,可实现发动机全转速范围内的榫齿均载。当k1≠k2,例如k1
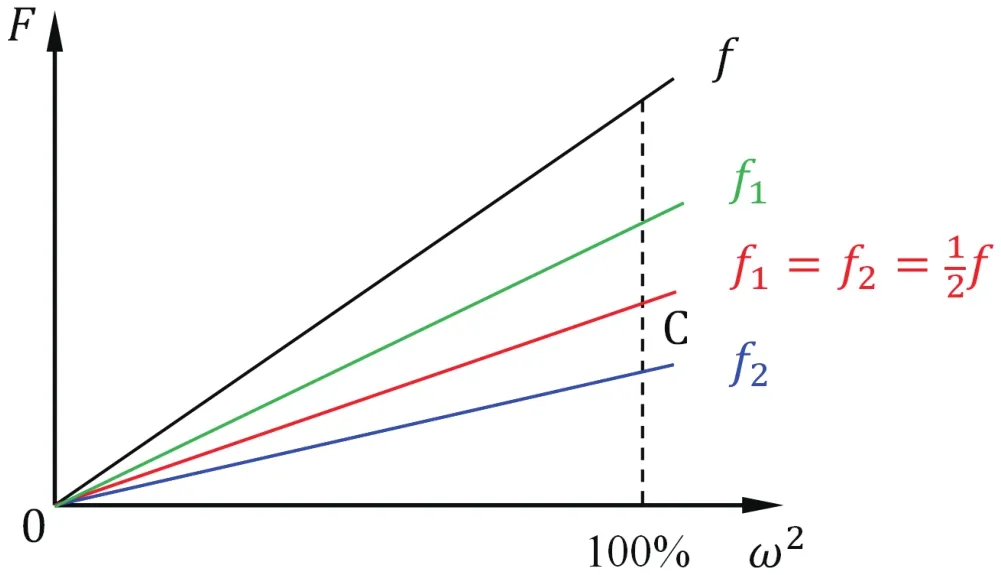
图3 等齿距榫齿载荷分配
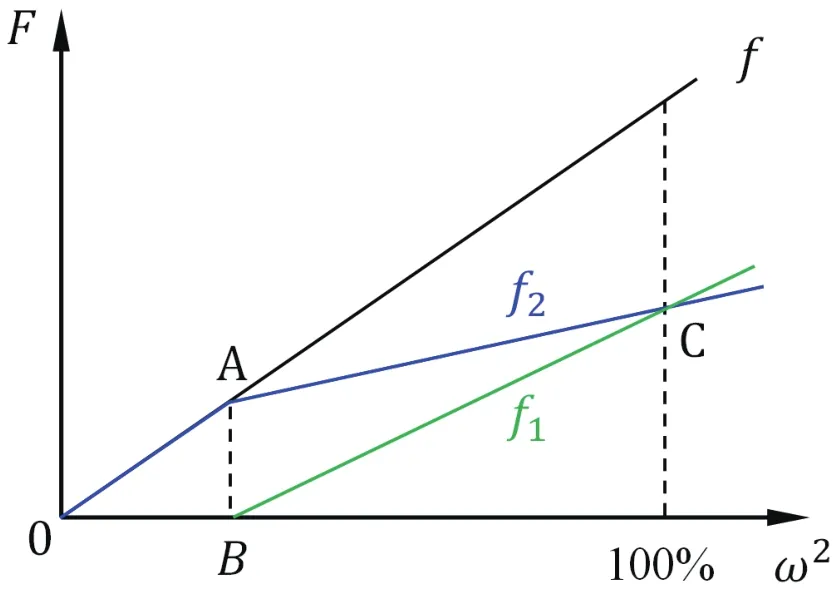
图4 不等齿距榫齿载荷分配
通过上述示例不难发现,用调整齿距的方法只能实现在某一个转速条件下的榫齿均载。一旦偏离该转速,榫齿的载荷分配就不再均匀,其不均匀程度与k1和k2的差异相关,刚度差异越大,载荷分配越不均匀。
2.2 三齿榫头
借鉴两齿榫头的等效刚度建模思路,可以得出三齿榫头的力学分析模型,如图5所示。由于结构的对称性,下面只讨论叶片榫头齿距小于等于轮盘榫头的情形。公式(2)、(3)、(4)中的符号Δ表示力的增量。
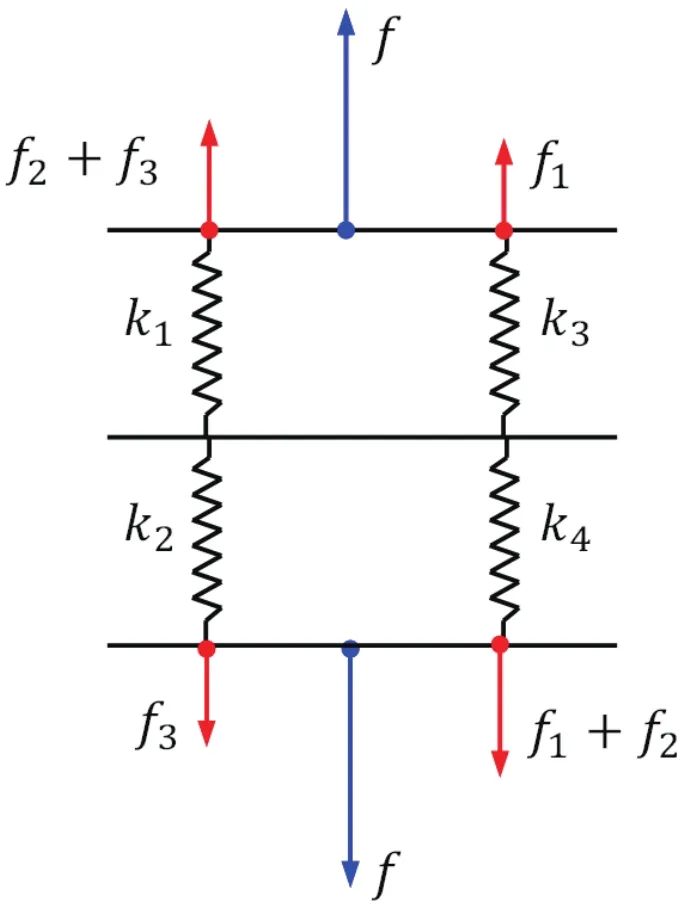
图5 三齿榫接等效刚度模型
(1)当三对榫齿均接触时,有
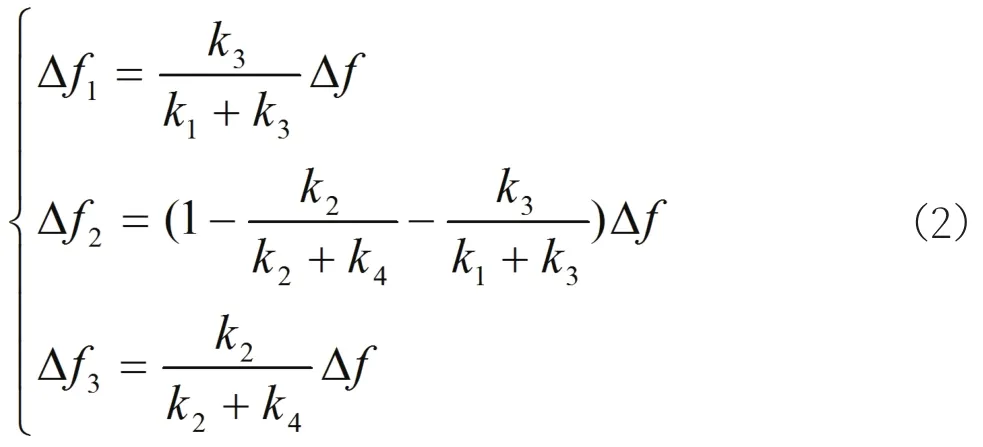
(2)当第一对榫齿脱开,第二、第三对榫齿接触时,有
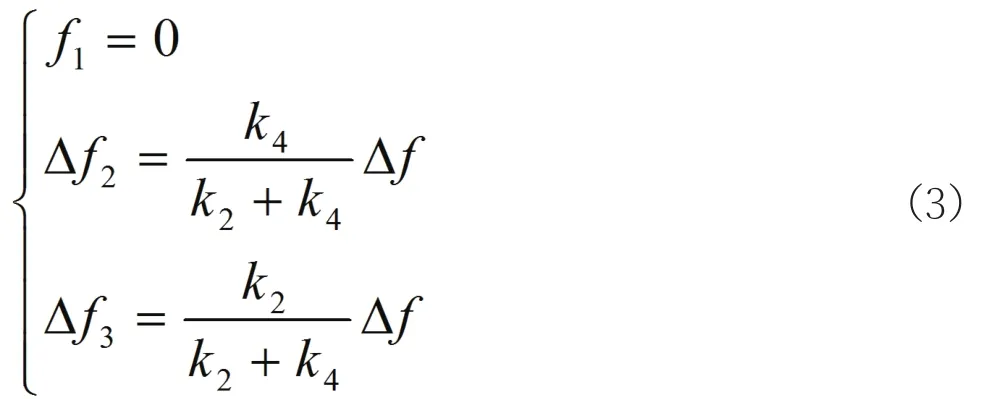
(3)当第二对榫齿脱开,第一、第三对榫齿接触时,有
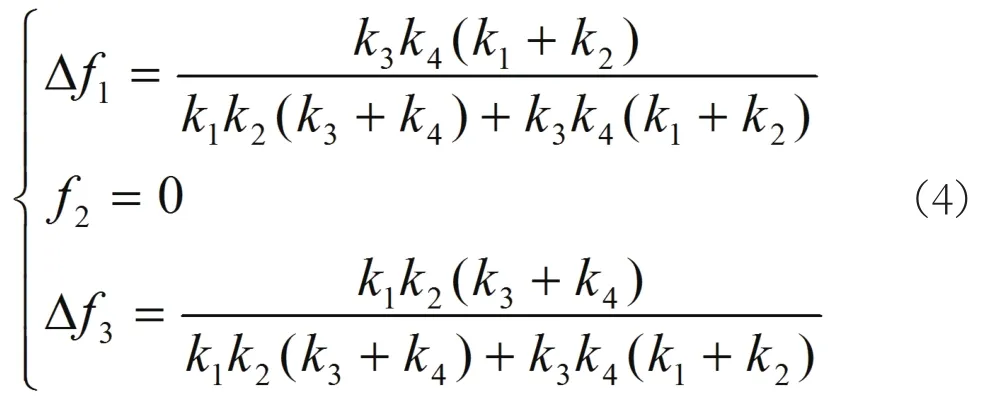
下面,我们通过一个示例来说明如何运用作图法求解榫头/榫槽齿距的调整量。假设有一个等齿距设计但载荷分配不均的榫接,f1、f2、f3分别如图6中线条0G、0D、0E所示。为了不使线条过多导致图形凌乱,假设在D点有f1=f2=f3=f/3。由公式(2)可知,当三齿均接触时,载荷分配满足恒定的比例关系。因此,过D点做两条直线CD和AD分别平行于0G和0E。CD线与横坐标轴交于点C,即表明当转速从C点继续降低时,第一对榫齿脱开。观察公式(2)和公式(3)可知,第一对榫齿是否脱开不会影响f3的斜率,因此AD是一条直线。过A点做垂线与横坐标轴交于点B。在转速BC段,由f2+f3=f,做线条BH表示f2。当转速低于B点,第二对榫齿脱开,所有的载荷均由第三对榫齿独自承担。因此,齿距调整之后,f1、f2、f3随转速变化的路径分别为0→C→D、0→B→H→D、0→A→D。
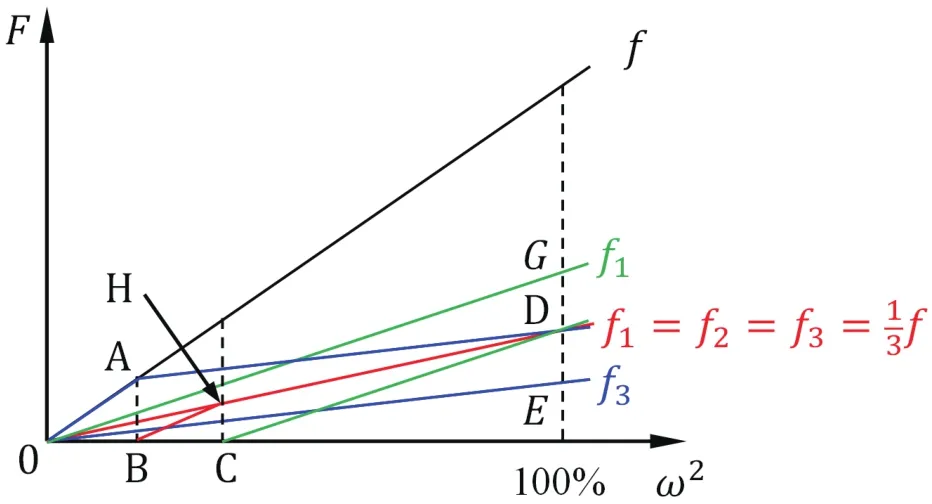
图6 三齿榫头载荷分配
榫头第二、第三榫齿间承受拉力fB发生的齿距变形量就是二、三榫齿间齿距的调整量δt2;同理,榫头第一、第二榫齿间承受拉力fC产生的齿距变形量就是一、二榫齿间齿距的调整量δt1。通过简单的计算,有
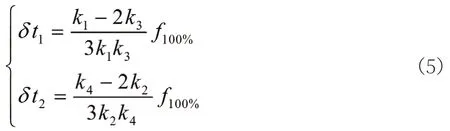
从上式可以看出,三齿榫接的刚度匹配若满足关系式k1=2k3,k4=2k2,则δt1=δt2=0,此时榫头/榫槽为等齿距设计,可以实现全转速范围内的榫齿均载。
3.结论
本文通过对榫接的受力进行分解,将分布力按集中力等效处理,建立了榫接的等效刚度力学分析模型,研究了齿距差异对榫齿载荷分配的影响,得出如下结论:
(1)齿距差异会改变各对榫齿之间的配合间隙,从而改变各对榫齿发生接触的先后顺序,进而调整载荷在榫齿之间的分配。
(2)齿距调整可以实现设计转速条件下各对榫齿之间的均载,一旦转速发生偏离,载荷分配就不再均匀,但可以保证0~100%转速范围内各对榫齿的载荷都不会超过设计转速下的平均值。
(3)从榫接正向设计出发,实现榫齿均载设计的最佳方法是榫头/榫槽的热态模型为等齿距设计,且叶片榫头与轮盘榫头之间需满足特定的刚度匹配关系。齿距调整,其实质是对榫接设计刚度不匹配的一种事后补偿。
