人人都做“小老师”*
——基于小组合作的深度学习改进
2023-01-11广州市荔湾区教育发展研究院
⦿广州市荔湾区教育发展研究院
蔡 琳
1 引言
《普通高中数学课程标准(2017年版)》[1]中提出:教师要把教学活动的重心放在促进学生学会学习上,积极探索有利于促进学生学习的多样化教学方式,不仅限于讲授与练习,也包括独立思考、动手实践、自主探索、合作交流等.新课标实施后,学生的学习方式有一定程度的改善,但合作的形式单一,多是线性,参与发言人数受限.
深度学习理论认为[2],学生应该在教师的引导下对知识进行“层进式”和“沉浸式”学习,强调学生应该在与教师、同伴、文本及自我的平等对话与真切交流中对知识进行理解和内化,从而生成新的个体化知识和意义理解.
基于此,作为课程的实施者,教师要积极思考建构多元化、多层次的小组合作学习方式,达到人人都做“小老师”,实现真正意义上的全员参与的深度学习.
2 异质化组合,人人有特长
小组合作要结合课堂观察和学情分析合理编组,以保证合作的有效性.本节课采用“组内异质,组间同质”的分组方法,既可以照顾学生之间的差异性和互补性,又能确保竞争的公平性.首先,根据学生兴趣、信息技术水平、表达、数学成绩等因素给学生编码A,B,C,D,全班学生就被分成了A,B,C,D四个类别;然后,按“S”形从每个类别中各抽1人组成4人小组,反复操作,直到分组完成;最后,再根据性别,意愿等微调,这样全班学生就被分成了若干个具有A,B,C,D四种特质的4人小组.现规定:小组内4名成员按特质编码分别对应称为“小老师A*”“小老师B*”“小老师C*”“小老师D*”,其中*号表示组别.本节课组内4位“小老师”的角色分配如下:“小老师A*”和“小老师B*”合作完成任务1,“小老师C*”负责任务2,“小老师D*”承担任务3.
3 深度化合作,人人有任务
3.1 精选内容,设计任务单
教师要基于教学目标、教学内容、教学对象,精心挑选探究性、拓展性、开放性等适合小组合作学习的内容,然后根据内容设置学习任务单.
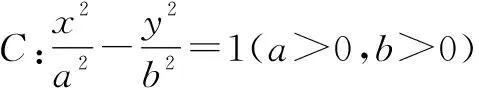
任务1: 请用多种方法解出此题.
任务2: 请挖掘此题的背景,并归纳考查了哪些知识,用到了哪些思想方法,蕴含了哪些核心素养.
任务3: 请以此题为题根,进行变式,至少一题,跨组交流解答.
3.2 自主探索,奠定合作基础
小组合作的基础是自主探索,在个体与文本和自我对话的过程中,完成知识储备的自我诊断,完成同化和部分修补.在此基础上,个体带着经验和问题进入下一个阶段的学习——组内合作交流.
3.3 组内合作交流,人人都是“小老师”
经过自主探索,人人“身怀绝技”或困惑,成员在知识的交流与思维的碰撞中,也逐步把别人的经验转化为自己的经验,最终具备参与活动的能力,成长为该活动的“小老师”.
下面是第三组内部交流任务1解法片段:
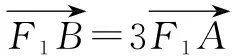
解法1:解析法“思得少,算得大”.
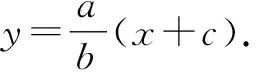
联立直线F1A与直线OA的方程,得
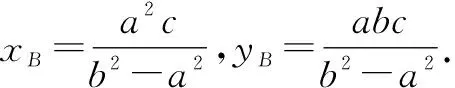
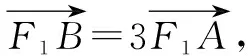
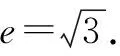
解法2:几何坐标“打配合”.
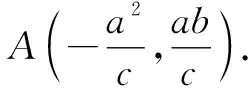
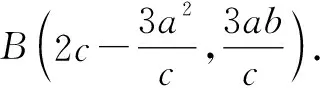
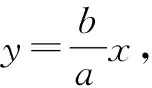
组内交流互助后,进一步细化任务,明确分工,为面向班集体跨组交流分享做好准备.
4 跨组式交流,人人都有收获
深度学习理论提倡“层进式”学习,强调对知识内在结构逐层深化学习.基于此,典例学习分为三个层次:解题—思想方法—变式.教师根据组内交流展示情况,选取几何法和3种典型变式跨组深度交流,请“小老师”们班级展示.
下面是教学中的一个片段,教学片段中的“小老师”是指台上展示的学生,台下的“小老师”暂称学生.
4.1 “层进式”学习第一层 一题多解,拓展思维
解法3:几何法大显身手.
“小老师B2”:我们先来看一个课件(演示GeoGebra软件),如图1所示,可知OA=a,AH=b,OH=c,现在拖动F,A,改变双曲线的形状,请同学们观察AH与EF有什么数量关系?
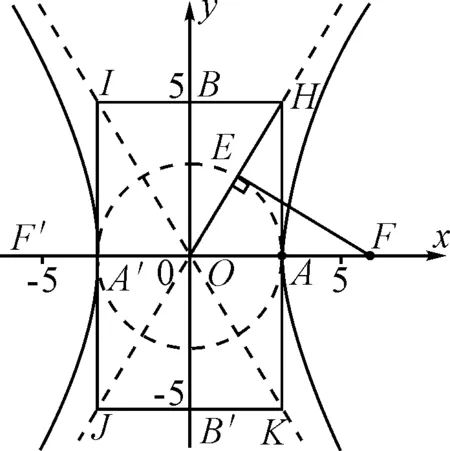
图1
学生齐答:EF=AH=b.
点评:史宁中教授说曾说过,数学的结果是“看”出来的,而不是“证”出来的,虽然看出的数学结果不一定正确,但指引了数学研究的方向.“小老师B2”首先通过引导学生观察双曲线的图形,“看”出焦点到渐近线的距离为b,增强了学生对试题的直观理解.
“小老师B2”:我们可不可以证明这个结论?
学生1:利用点到渐近线的距离公式,求F1到直线的距离,可以证明(证明过程略).
学生2:如图2所示,可证明△OEF≌△OAH.(过程略)
“小老师B2”:我们来看具体的解答过程,如图2.
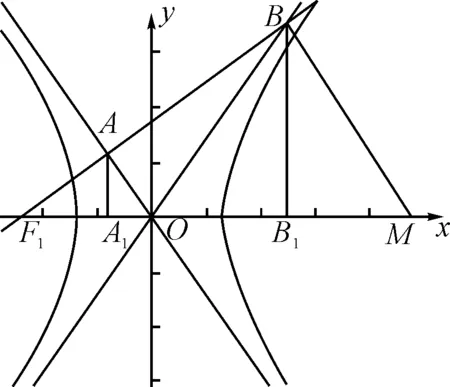
图2
根据结论,可知焦点到渐近线的距离|F1A|=b.
在Rt△OAF1中,OF1=c,于是OA=a.过B作BM垂直于F1B,交x轴于点M,于是
于是|OM|=2c,|AB|=2b,|BM|=3a.
过A,B分别作AA1,BB1垂直于x轴,垂足为A1,B1,于是△AA1O∽△BB1O,可得
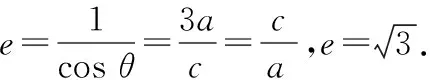
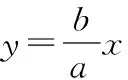
点评:通过合情推理得出焦点到渐近线的距离“二级”结论.并用演绎推理加以证明,学生的思维经历了从感性认识到理性认识的升华.由此可见,记住一些小结论是有助于解题的.
4.2 “层进式”学习第二层 师生对话,感悟升华
教师:谢谢“小老师B2”启发式的讲解和同学们的积极配合,下面我把第三组的两种解法投影出来,同学们比较3种解法,你能得到什么结论?
学生5:几何法计算量最小,坐标法计算量大.
教师:不错,所以我们在求解析几何试题时,要尽量挖掘试题的几何特征,先直观感知,再坐标法.但是当无法挖掘几何条件时,只能采用坐标运算.本题求a,c关系式时,要在试题中寻求“等量关系”,那么解法1、解法2的等量关系各是什么?
教师:同学们回答的很正确.我们在找等量关系时,还要善于挖掘试题中隐含的等量关系.下面请一位“小老师”归纳总结一下,这道题的背景是什么?考查了哪些知识点?用到了哪些方法?渗透了哪些核心素养?
“小老师C7”:本题改编自2019年全国Ⅰ卷第16题,考查了平面向量、双曲线的渐近线和离心率,解题方法可以采用解析法、几何法,数学思想方法有数形结合、方程思想,渗透了逻辑推理、直观想象和数学运算核心素养.
教师:数形结合和方程的思想分别在哪里体现的?
“小老师C7”:根据题意画出图形,所以有数形结合,解法1和解法2列a,c关系式时用到了方程的思想.
点评:罗增儒说数学思想是数学知识通往数学核心素养的桥梁.通过师生对话,把学生从碎片化的知识学习,引向知识系统化,思想方法提升化的深度学习,有助于学生核心素养的达成.
4.3 “层进式”学习第三层 变一变,迁移应用
教师:下面有请“小老师”们来展示他们组的变式,并跨组交流解答.(过程略)
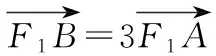
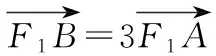
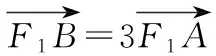
点评:通过让学生自己变式,引导学生多角度、多方面、多层次思考问题和分析问题,培养学生的发散思维和批判思维.学生能够把问题符号化,说明高阶思维的发生,数学抽象素养的达成.同时强调符号计算,在落实数学抽象素养的同时,培育了数学运算核心素养.
5 激励性评价,人人都有发展
课堂结束,学生通过课堂观察量表[3]从语言、辅助方式、有效性和时长等方面对“小老师”教学行为展开激励性评价.通过激励性评价,让学生意识到小组合作学习的重要性,从而提高成员在小组活动中的积极性,同时也让学生意识到自己在小组合作中的重要性,提高学习数学的兴趣和自信心.
6 结束语
总之,小组合作学习契合新课程的核心理念,在深度学习理论视野下,人人都做“小老师”的合作学习更是极大地调动了全体学生学习的积极性和主动性,体现了以生为本,学生是学习的主人.通过组内、跨组多元化、多层次的小组合作学习,不同层次的学生在同一内容中各有所获,不同难度的内容也得到有效落实[4],实现了从关注教师的教到关注学生的学,体现了深度教学与深度学习的一致性,能够促进数学学科素养落地,真正落实“立德树人”五育并举的教育理念.
