课程思政视域下高中数学教学研究
2023-01-11吉林师范大学
⦿吉林师范大学
赵金凤
1 “课程思政”理念概述
“课程思政”是2014年提出来的,在习近平总书记的大力倡导下,各校都开始积极地将课程思政的理念融合到各科教学中.课程思政中的课程的含义[1],即通过各科课程对学生进行思想政治教育,达到立德树人的目的,促进当代学生心理和精神的健康发展,培养全面发展的高级人才.
高中数学是学生思维发展的转折期,这一时期要对学生进行积极有效的综合教育.高中生已经初步具备成人意识,正确思想觉悟的形成需要教师在日常教学中进行引导,培养一定的数学思维[2],在数学上得到综合发展.
2 “课程思政”理念与高中数学教学的融合
新课改后,高中数学课程更加注重对学生的马克思主义思想、历史文化、人生观、价值观等的教育,而不只是过去单一传授数学基础知识,其致力于学生的全面发展,使数学课程得到升华,使学生在数学学科上得到最优的发展.
2.1 马克思主义思想与高中数学教学的结合
(1)矛盾的同一性.
解析几何领域知识是矛盾的同一性这一规律明显的体现,点对应着坐标,坐标对应着轴,其中轴是相互依存的.
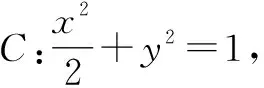
分析:教师引导学生,要求直线的斜率,就要知道A,B两点的坐标,故首先设出A,B坐标,然后根据得到的关系,利用斜率公式求解.

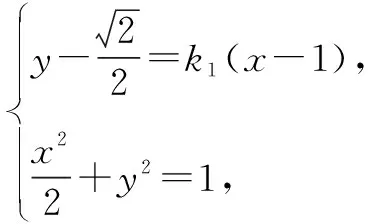
故直线l的斜率
本题在求直线斜率时,将分子中的y1-y2利用x1,x2来表示,转化成只与x相关的关系式,再根据x1,x2之间的关系得解,体现了轴的相互依存与转化.教师在讲解时可以由此渗透世间万物都有两面性且相互依存,看事物要全面,在事物的转化中求发展.
(2)主要矛盾与次要矛盾.
高中数学中一个题目可能包含多个变量,对于这类问题教师要引导学生找出主要矛盾与次要矛盾,循序渐进地解决.

分析:此题中有三个变量,教师引导学生找出题眼,根据ab+ac=4得出b+c,将b+c代入原式,再根据基本不等式求解.


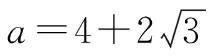
本题中有三个变量不好解决,而抓住主要矛盾问题就变得简单明了.在日常生活中会遇到很多困难,教师要通过此题引导学生先解决主要矛盾,循序渐进,所有问题都会迎刃而解.
(3)否定之否定规律.
否定之否定规律在高中数学中表现为正难则反,解决问题的办法有多种,数学中有些问题正面解决会很复杂,此时如果逆向思维会有柳暗花明又一村的感叹[3].
例3某学校要举行夏季运动会,打算从从5名男生和4名女生组成的田径运动队中选出4人参加比赛,要求男、女生都有,则男生甲和女生乙至少有一人入选的选法为多少种?
分析:此题如直接求,要分成三类,较麻烦,可以考虑从反面来求,即利用总的选法种数减去男生甲和女生乙都不入选的选法种数.

通过此题,教师要教导学生遇事要学会变通,多换角度思考问题,多思考,多行动.
2.2 数学文化与高中数学教学的结合
古有《九章算术》《周髀算经》等,今有各个数学家的伟大发现与创造.数学不仅是科学,更是一种文化,让学生了解数学文化十分必要,这在近几年的高考试题中也有体现.
(1)数学文化与数列的结合.
例4世界上最古老的数学著作《莱因德纸草书》中有这样一道题目:把60磅面包分给5个人,使每个人所得成等差数列,使较大的两份之和的一半等于较小的三份之和,则最小的一份为多少磅?
分析:此题将数学文化与数列问题进行结合,首先将每个人分得的面包磅数抽象成等差数列的项,然后利用等差数列知识求解.
解析:设最小份为a1,且公差为d,根据题意可得

(2)数学文化与概率的结合.
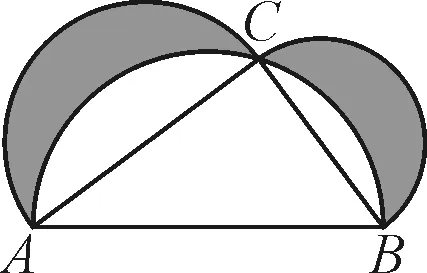
图1
例5希波克拉蒂有一个著名的“月牙定理”,如图1所示,在直角三角形ABC中,BC=1,∠CAB=30°.将整个图形记为区域M,若向区域M内随机投入一个骰子(骰子大小忽略不计),求骰子落入“希波克拉蒂月牙”(即图中阴影部分)的概率.
分析:此题将数学文化与概率问题结合,考查几何概型的概率知识.首先应求出整个区域的面积,再求出月牙的面积,月牙面积与总面积之比即为所求.

(3)数学文化与三角函数的结合.

分析:此题是数学文化与三角函数的结合,考查诱导公式的相关知识,可将b用a来表示,再代入原式求值.

文化是劳动人民千百年来积累下来的宝贵财富,学生学习数学文化既了解了数学文化方面的知识,又提升了学习数学的兴趣,丰富了精神世界.教师在讲授新课或习题的过程中可以有侧重地融入数学文化方面的内容,讲个数学小故事,或出一个数学著作中的经典题目,长久实施下去学生数学兴趣会得到提高,数学思维也在无形中被培养起来,对于教师来说也是提高自身综合素质的有效途径.
2.3 社会事件与高中数学教学的结合
当今世界飞速发展,科技、医疗、教育、军事等都在稳步向前.对教育来说,不能只把目光局限在书本上,而要把知识与现实生活进行融合[4].数学题目中融入当今时代信息是向学生展示国家实力,了解国家大事,促进学生努力学习的有效途径.

(1)记ξ表示确诊病人的人数,求ξ的分布列;
(2)因为疫情正处于上升期,医院不断接收需要检测的疑似病人,为了提高效率,医院采取以下措施:从收治的一批疑似病人中随机抽取一人进行检测,若是确诊病例,则这一批所有人员都需要检测,若不是确诊病例,则继续随机抽取,直到抽到确诊病例为止,并且规定抽样的次数不超过n次,在抽样结束时,抽得的非确诊病人人数为η,求η的数学期望.
分析:本题结合了新型冠状病毒的信息,考查学生概率及二项分布相关知识.
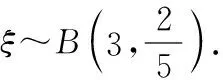
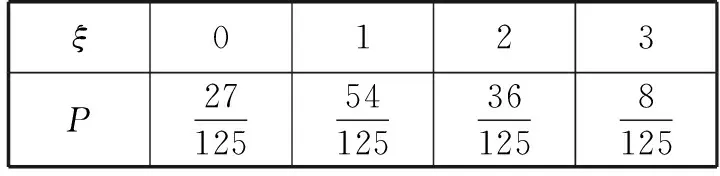
表1

新冠是现在还在世界上肆虐的病毒,医护人员都冲在第一线保护人民的生命安全.在讲解此题时,教师要告诫学生遵守防疫守则,日常生活中更要注意卫生;要激起学生的爱国之心,做到自律自觉,不给国家和社会制造麻烦;同时,也要让学生感受到国家的强大,作为一个中国人应该感到自豪.

图2

(1)求氢能源环保电动步道的长;

分析:此题将冬奥会与数学知识进行结合,考查学生解三角形的相关知识,利用解三角形的相关知识求解.
解:(1)根据二倍角公式,得
利用余弦定理,得
AC2=AD2+CD2-2AD·CD·cosD=12.
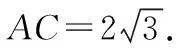
北京冬奥会刚刚落下帷幕,不论是开幕式还是比赛过程都十分振奋人心,与数学知识的结合更能引起学生兴趣,也让学生体会到数学知识的实践价值.数学可应用在各个领域,让学生深刻领悟到数学知识的重要性与实际应用性,提升学生数学素养.
3 总结
课程思政融于具体课程的教学需要教师进行深入细致的研究与设计[5],如何达到最优化的效果值得教育界反复思考.教师可以在新课讲授和题目讲解中渗透课程思政的相关理念,使学生具有积极正确的人生态度,把学生培养成为全面发展的综合型人才,达到立德树人的教育目的.
