在接续研究中发展理性思维
——以“复数的乘、除运算”为例
2023-01-11湖南省株洲市五雅中学
⦿湖南省株洲市五雅中学
阳志长
1 引言
数学学习更多带有研究色彩,是通过获得一个个数学研究对象的学习过程,使个体研究心理、思路、方法、方式、思想等获得持续变化与发展,形成具有个性特征的数学思维的过程.数学思维是一种理性思维,突出表现在思维的连贯性、严谨性、批判性、创新性等品质方面.新课程提出“优化课程结构,突出主线,精选内容”[1]的课程理念,本质是抓住获得各个数学研究对象的过程,采取单元教学方式,发展学生的理性思维.
“复数的乘、除运算”是新课标教材第七章“复数”第二节“复数的四则运算”[2]第二课时的教学内容.“因为高考中的复数题非常简单,所以许多老师对复数的教学也不太上心”[3],以致于简单了事,在第二节第二课时匆忙落下第七章教学“帷幕”.“复数是一类重要的运算”[1],学生已经理解引入复数的必要性,如此“谢幕”,他们感受不到复数应用的广泛性;“复数源于纯粹的数学推理,是理性思维的产物”[3],复数的乘、除运算不仅是研究一类运算对象“思维链”的关键“节点”,而且是认识复数概念、复数的三角表示,以及发展理性思维的重要载体.
2 对接思考,培养思维的连贯性
与复数的加、减运算(简称“一级运算”)类似,教材直接规定复数的乘、除运算(简称“二级运算”)的乘法法则.为什么可以这样规定?基于复数的代数表示,在探索复数一级运算时,类比两个多项式相加、减,学生已经感受到复数加法法则“规则”的合理性,以及研究一个运算对象的“基本套路”.为让学生了解复数“二级运算”产生的背景和学习的必要性,本课时需要突出第一个教学重点,“复制”这个“基本套路”,抽象、推导出复数乘法法则.
(1)PPT呈现问题1:设z1=a+bi,z2=c+di(a,b,c,d∈R).我们知道,z1+z2=(a+c)+(b+d)i,z1-z2=(a-c)+(b-d)i,两个复数的和、差是一个确定的复数.那么,接下来应该研究什么?可以怎样研究呢?
(2)学生思考、回答问题.教师引出并板书本节课的研究主题,引导学生回顾第一课时研究的“基本套路”,获得研究复数乘法运算方法:类比两个多项式相乘.
(3)学生演练、推导,教师规划板书位置,让一位学生代表板书、推导.
(4)教师“点击”,同化研究方法,导引学生阅读教材第77页的相关内容,让他们感受研究方向的正确性、“规则”的合理性,得到复数的乘法法则(a+bi)(c+di)=(ac-bd)+(ad+bc)i,以及两个复数的积是一个确定的复数.
(5)PPT呈现问题2:得到复数的乘法法则后,按照研究复数加、减运算的“基本套路”, 接下来应该研究什么?怎样研究呢?
(6)学生思考、回答问题,教师规划板书位置,让三位学生代表展示推导过程.
(7)教师 “点击”, 再次同化研究方法,得到:复数乘法运算律、对加法的分配律.然后,简单小结一下研究复数乘法运算的“基本套路”,让学生进一步得到各步的意义建构.
以上的对接、思维活动,围绕研究一个运算对象的“基本套路”,通过提供“先行组织者”、激活“情境与问题”的途径,传承复数加法运算的研究方式,并在类比思考、接续研究中,培养学生思维的连贯性,以及数学抽象、数学建模等核心素养,并形成对运算研究对象探索的方向感,以及积极的认知情感、态度与价值观.
3 跟进思考,培育思维的严谨性
得到复数乘法法则及其运算律后,教材通过例3、例4,示范复数乘法运算的“思维与表达”,在此基础上提炼“乘法公式”.同属二级运算,为不割裂研究“链条”,本课时需要突破第一个教学难点,变通“套路”,推导、概括出复数除法的法则.
(1)PPT呈现问题3:类比多项式的乘法运算,我们得到了复数的乘法法则及其运算律.多项式乘法一个显著标志是可以用“乘法公式”简化运算.那么,复数乘法是否有相应的公式呢?
(3)PPT呈现问题4:二级运算还有除法.那么,两个复数能否相除?如何研究复数的除法呢?
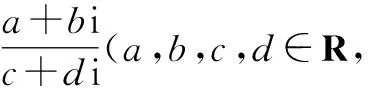
(5)教师 “点拨”, 顺应研究方法:遵循“基本套路”,根据运算对象的结构特征,展开联想,变更类比对象,分析、研究问题.简单小结,突出理解与应用特色:复数乘、除运算分别类比多项式乘法、根式除法运算.
以上思考与探索过程,按照一个运算对象的研究过程,通过体现共性、突出个性,延续复数加减运算的研究方式,顺应知识,并在跟进思考、接续研究中,突破教学难点,培养学生思维的严谨性,以及逻辑推理、数学运算等核心素养,建立相关研究的“知识与技能”“思维与表达”“交流与反思”.
4 换位思考,增强思维的批判性
得到法则后,紧接着就是法则的应用,需要突破第二个教学难点:法则的正确理解与灵活应用.
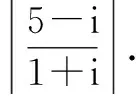
(2)学生独立思考,自主练习.6分钟后,展示多位学生代表的计算过程,学生与教师一道矫正、点评,鼓励其他学生提供不同的计算思路或方法.
(4)PPT呈现例2.在复数范围内解下列方程:①x2+2=0;②ax2+bx+c=0,其中a,b,c∈R,且a≠0,b2-4ac<0.
(5)学生独立思考、提供解题方案后,让学生对照教材第79页例6的“分析”与“解”发表意见或提出问题.然后,教师点评、提炼:例2第②题为一般情形,教材给出的“解”体现了求解实系数一元二次方程的“根本大法”——配方法,转化为特殊情形;虚数与复数的引入缘于解方程时遇到的负数开平方问题,作为复数及其运算应用的一个重要方面,有了“求根公式”,可以直接利用它求实系数一元二次方程在复数范围内的根,或将实系数二次三项式在复数范围内分解因式.
以上探讨过程,按照研究一个运算对象的进程,采用提供多样性素材、激发应用情境的方法,使研究复数加减运算的方式得以改造,并在换位思考、接续研究中,突破教学难点,增强学生思维的批判性,完善一个运算对象的研究过程,解决数系扩充后复数运算的封闭性、应用性等问题,使一个运算对象的研究“套路”找到比较稳定的“固着点”.
5 接续研究,发展思维的创新性
数学研究,不止于解决问题,还要回归研究历程,获得 “再出发”的能量.课堂最后环节,还需要上升到数学思想高度,突出第二个教学重点:完善研究一类运算对象乃至一类数学对象的“基本套路”、行动方案.
(1)学生小结.可以使学生明晰:复数的乘、除运算,类似于整式的乘法、根式的除法运算,乘法满足交换律、结合律及对加法的分配律,可以用乘法公式简化运算,结果是一个确定的复数;与实数运算、三角恒等变换一样,复数运算常要抓住运算对象特点,考虑运算依据,设计运算程序,达到运算目标.
(2)变更情境.让学生浏览教材第75至79页的内容,结合黑板板书,回顾课堂学习、研究历程,谈学习体会,或提交问题.
(3)教师凝练.在肯定学生的突出表现、所作小结的基础上,凝练出研究复数乘除运算的思想方法——类比迁移法,以及研究一个运算对象的“基本套路”:“背景—概念—基本性质—运算及其几何意义、运算律—联系与应用”[3].引导学生发现尚没有研究的问题:复数乘、除运算的几何意义,以及复数乘方、开方运算及其几何意义.凸显研究一类运算对象的思维轨迹,鼓励学生接续研究教材第81页“代数基本定理”及选学内容“复数的三角表示”,为后续课时的研究性学习作好准备.
上述梳理与凝练过程,采取参与小结、多向对话的策略,将“小结权”还给学生,引导学生自主梳理一节课的知识,重视阅读教材和学习小结,开展与教材、自己对话.更好地发挥教师的引领作用、开拓视野,指导学生开展与同学、老师对话,系统认识运算对象研究的过程和数学学习本身,重视研究数学对象的思想方法、绘制思维蓝图,将数据分析、数学建模等核心素养的培养落实到课堂; 再现复数研究的“情境与问题”“思维与表达”“交流与反思”,让学生明白为什么虚数以及复数概念的引入会经历一个曲折的过程,领悟其中蕴涵的数学家的想象力、创造力,使研究复数“二级运算”的流程得以“再造”,发展思维的创新性.
6 结束语
复数的乘、除运算是复数运算“思维链”的关键“节点”,主张按照研究一个运算对象的“基本套路”,优化设计,通过对接思考、跟进思考、换位思考、接续研究的方式方法,使研究复数一级运算的“基本套路”得以“传承、延续、改造、发展”.在接续研究中重构研究一类运算对象的“基本套路”,培养思维的连贯性、严谨性,增强思维的批判性,发展思维的创新性.新课程改革正在如火如荼地进行,广大教师要认真钻研课程标准和教材,立足各个课时、各个单元、各条主线,以及各个、各类研究对象,优化设计,课时落实,单元突破,主线推进,合力锻造学生数学思维的必备品格和关键能力,让他们在接续学习、研究中发展理性思维,赓续数学家不屈不挠、精益求精的精神血脉, 落实“学生发展为本,立德树人,提升素养”[1]的根本任务.
