基于深度学习的高中数学微专题教学策略*
2023-01-11福建省德化第八中学
⦿福建省德化第八中学
方章颜
1 引言
深度学习理念的提出使数学教师对课堂教学方式有了新的认识和理解.高中数学课堂不应该只是简单传授知识及讲解方法,而应该是学生体会知识生成的动态过程,不断完善自己的知识体系,发展自身的理性思维.深度学习不仅有利于培养学生的理性思维,更有利于培养学生注重学习本身及知识间的关联性和层次性[1].而微专题教学是围绕主干知识的一个中心点对知识进行拓展,它能有效促进深度学习,是培养学生深度学习的最佳操作平台[2].
2 基于深度学习的数学微专题教学的必要性
数学深度学习是指学习者在低层学习基础上形成更加抽象的表示特征或属性类别,将之内化并能迁移到新的情境中,做到举一反三、融会贯通来解决问题的一种学习方式,具有整合内容、建构知识、理解批判、迁移运用等特征[3].
首先, 深度学习理念决定了微专题教学的必要性.数学学习本质要求学生进行深度学习,深度学习过程中对数学本质的理解、相关思考和学习策略,都有助于学生对一类知识的掌握和方法的迁移[4].而微专题教学不仅提供了深度学习所需要的大环境,也有利于学生形成清晰的知识网络、系统的学习方法,为逐步提高数学理性思维的培养创造了条件[2].
其次,微专题教学的特点决定了深度学习的可能性.微专题教学内容具有灵活性,可以是学生的疑难点,也可以是学生感兴趣的问题.微专题教学从“知识-方法-思想”的角度引导学生思考和解决问题,强调学习内容的联系性,循序渐进.微专题的教学内容选择的灵活性、内容编制的实用性和教学方法的有效性都决定了开展深度学习的可能性.
最后,发展学生数学核心素养要求学生进行深度学习.《普通高中数学课程标准(2017年版)》明确指出:数学教学的根本任务就是发展学生的数学核心素养[5].深度学习可以培养学生的高阶思维和关键能力,因此,教师要引导学生进行深度学习,用数学的眼光去认知世界,用数学思维去分析问题和解决问题,最终形成学科核心素养,使其受益终身.
3 基于深度学习的数学微专题教学策略
《课标 (2017年版)》明确指出:通过数学的学习,学生能获得进一步学习以及未来发展需要的数学的基础知识、基本技能、基本思想、活动经验,提高从数学角度发现问题、提出问题、分析问题和解决问题的能力[5].从高中数学知识与初中数学知识的比较来看,高中数学知识比较抽象,学生难于理解和领悟.因此,教师要合理运用教学策略,引导学生进行深度学习.本文以含“新定义信息”背景的数列问题微专题教学的第一课时为例,阐述利用微专题进行深度学习的教学策略.
3.1分析学情,设计科学合理的学习目标
科学合理的教学设计是有效教学的保障.教师要联系学科的知识和思想方法,避免碎片化的设计;设计整合性的学习活动,培养学生思维能力和迁移能力,解决新情境中的问题.在设计教学目标时,教师不仅要考虑学生的认知水平和认知规律,也要明确知识整体结构,处理好知识的纵横联系,从知识的点、线、面进行拓展,从旧到新、从具体到抽象,由浅入深、循序渐进.
例如,含“新定义信息”背景的数列问题.该微专题有如下难点:(1)学生在面对新的概念与规则时不能抓住信息的关键部分;(2)由于传统题目与新信息问题在问题提法上表达的差异,学生找不到解决问题相关的知识点.传统题目通常直接表明考查哪些知识,例如“求通项”“求和”,而新信息问题则没有直接提及要运用的知识,学生很难找到解题的方向.因此,该微专题第一课时的教学目标设计如下: ①了解含“新定义信息”背景的数列问题特征;②掌握含“新定义信息”背景的数列问题的解题技巧;③运用技巧解决此类问题.
3.2 设置情境,鼓励学生开展自主探究学习
问题1含“新定义信息”背景的数列问题指的是什么?
归纳: 含“新定义信息”背景的数列问题是指根据即时数列定义(如新概念、新法则、新定理、新运算等)去解决有关数列问题.
例1(2016·全国卷Ⅲ)定义“规范01数列”{an}如下:{an}共有2m项,其中m项为0,m项为1,且对任意k≤2m,a1,a2,……,ak中0的个数不少于1的个数.若m=4,则不同的“规范01数列”共有( ).
A.18个 B.16个 C.14个 D.12个
问题2与传统数列问题比较,含“新定义信息”背景的数列问题有什么特点?
归纳: 通过定义新概念来创设问题情境,要求学生阅读理解题意,依据提供的信息,联系所学,创造性地解决问题.特点一,新的概念与规则;特点二,考查的知识点隐藏较深.
设计意图:本环节的设计旨在基于原有数列基础知识,利用问题引导学生进行自主探究,构建自己的知识结构.设置问题情境是教师引导学生进行深度学习的重要途径.围绕某个知识或思想,开发本源性问题,不仅能激发学生兴趣,还可激活原有的认知及经验,进行迁移应用.本环节设计两个问题和提供典例创设情境引入课堂,让学生独立思考,分享观点,随后利用集体力量,从旧知到新知,不断总结,形成较为严密的含“新定义信息”背景的数列问题的认知,为接下来的教学任务奠定基础.
问题串起了数学课堂的教学活动,是数学学习的载体.所以,教师在优化创设问题情境时,要遵循班级学生的学习情况和认知规律,激发他们的学习兴趣,引导他们自主探究学习.深度学习不是单纯的、线性的静态变化过程,而是多维、综合的动态发展过程. 所以,教师要善于围绕某个知识点或数学思想设置问题情境,设计数学问题串来引导学生开展自主探究式学习,培养学生创造性解决问题的能力.
3.3 深入探究,培养学生数学思维品质
问题3如何解决含“新定义信息”背景的数列问题?
例2(2020·北京十中期中试题)定义“等积数列”:如果一个数列从第2项起,每一项与它的前一项的乘积都等于同一个不为零的常数,那么这个数列叫做等积数列,这个常数叫做等积数列的公积.已知数列{an}是a1=2,公积为-6的等积数列,则a3=______;数列{an}的前n项和Sn=______.
归纳:首先,认真阅读题目信息,明确新定义(包括名称和符号);其次,联系已有知识,探求解题方法;再次, 转化新定义中的知识,若是运算法则,直接按法则计算,若是性质,要判断它的适用性.
问题4如何寻找含“新定义信息”背景的数列解答题的突破口?
例3(2019·江苏高考真题)定义首项为1且公比为正数的等比数列为“M-数列”.
(1)已知等比数列{an}(n∈N*)满足:a2a4=a5,a3-4a2+4a1=0,求证:数列{an}为“M-数列”;
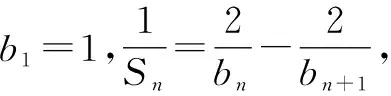
①求数列{bn}(n∈N*)的通项公式;
②设m为正整数,若存在“M-数列”{cn}(n∈N*),对任意正整数k,当k≤m时,都有ck≤bk≤ck+1成立,求m的最大值.
归纳: 在解答题中,新信息问题通常在设置问题时,具有“层层递进,环环相扣”的特点,第(1)问通常是创设数列知识点的定义和背景,第(2)问和第(3)问通常是数列知识的应用.故在解答时,要关注前面问题的解答过程与结论,抓住“新信息”这一特点,才能找到突破口.
设计意图:本环节的设计,旨在以问题引导学生深入探究含“新定义信息”背景的数列问题的特点,多角度探究它的特征,结合数列的基础知识,探求解题的基本策略和技巧. 在解答题中,新信息问题的设置特点——层层递进,环环相扣,即前面问题的解决是为后面问题的解答做好铺垫.然而很多学生难于发现其中联系,导致增加解题难度.虽然在设置问题时,含“新信息”背景的数列问题与传统的数列问题存在差异,但其根本都是一些基础知识与方法,所以要引导学生在考虑问题时向基础知识靠拢,有利于找到线索.分类讨论要遵循先易后难的原则,从相对简单的情况开始,去发现复杂情况的一些通用的做法与思路,有章可循.
数学学习需要大量的实践.教师可以利用微专题的优势,引导学生对某一数学知识或思想方法进行深入探究,这不仅能充分发挥学生学习的主动性,从中获得成就感,也可以让学生在自主探究学习中, 培养数学思维能力,例如学会发现问题、分析问题和解决问题.当然,教师在创设问题情境时,要特别注意设置的问题要有层次性,从具体到抽象,逐步深入,注意数学知识点之间的转换.
3.4 巩固提升,引导学生品味数学思想
问题5自己能否运用以上方法来解决含“新定义信息”背景的数列问题呢?
例4(2018届江苏省南京市三模)若数列{an}满足:对于任意n∈N*,an+|an+1-an+2|均为数列{an}中的项,则称数列{an}为“T数列”.
(1)若数列{an}的前n项和Sn=2n2,n∈N*,求证:数列{an}为“T数列”;
(2)若公差为d的等差数列{an}为“T数列”,求d的取值范围;
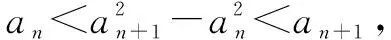
设计意图:引导学生及时巩固能保障微专题教学的有效性.本环节的设计,旨在利用问题去巩固新知,归纳总结,在实践中学会举一反三,真正掌握含“新定义信息”背景的数列问题的解题技巧,并灵活运用它去解决问题.同时,引导学生进行知识梳理, 把零碎的知识整体化,完善学习方法体系, 品味数学思想,有助于提高学生的学习技能,逐步形成学生的高阶思维能力.
在学习数学时,学生只有深刻去体验和真正深入思考,才能理解、把握数学知识和抓住数学本质. 深度学习让学生通过思考和探究,掌握数学问题背后的规律,培养学生思考问题和解决问题的能力,形成数学学科核心素养.深度学习理念不仅提倡学生改变学习方式,也引起教师反思自己的教学思想和教学方式.
4 结束语
在开展数学微专题教学时,教师要利用其“以小见大”的优势来引导学生找到问题的切入点,引导学生去发现问题和探究问题,进行深度学习.具有针对性、灵活性和高效性等特点的微专题教学方式更有利于帮助学生构建完整的知识体系, 形成科学的学习方法体系,提高学习效率.为更好地发挥微专题教学的有效性,引导学生进行深度学习, 教师应该根据不同阶段的学习特点来设置微专题.例如在进行基础知识点的教学时,应该以“点”来开展微专题教学,力求让学生掌握每一个知识点. 在复习阶段可以打破教材原来的顺序,整体规划复习内容体系,力求帮助学生将知识由“点”连成“面”.在设置微专题时应该侧重知识链,要求学生掌握相应的解题技巧和方法. 同时,在开展微专题教学时,教师要注重探究,讲练结合,让学生在探究过程中体验知识的魅力,感受学习的乐趣.教师可以灵活地根据专题内容选择讲练方式,例如,当专题知识难度较大时,教师可采用先讲再练的方式;当微专题知识难度较低时,就可采用先练再讲的方法.不管是何种方法,在教学中都要侧重“讲方法”“讲思路”“讲技巧”,才能在基于原有的知识基础上让数学能力从本质上得到提升.
深度参与是深度学习的前提,深度探究是深度学习的重点,深度反思是深度学习的延伸[2].只有让学生去实践和体验,才能真正深化对知识的理解,完善自身的知识体系,提升数学思维能力.深度学习让学生在创设的情境问题中体味数学的魅力和数学思想,在反思中学会举一反三,用数学思维去分析问题和解决问题,最终发展数学学科核心素养.
