结构影响线识别:反问题可识别性分析与降维贝叶斯不确定性量化
2023-01-04慕何青庞振浩
慕何青,庞振浩,王 浩,苏 成
(1. 华南理工大学土木与交通学院,广东,广州 510641;2. 华南理工大学亚热带建筑科学国家重点实验室,广东,广州 510641;3. 中国地震局工程力学研究所地震工程与工程振动重点实验室,黑龙江,哈尔滨 150080;4. 东南大学土木工程学院,江苏,南京 211189;5. 东南大学混凝土及预应力混凝土结构教育部重点实验室,江苏,南京 210096)
结构影响线描述了以移动单位集中荷载作为输入、以指定截面静力响应作为输出的映射关系[1],其直接反映结构的实际状态。因此,结构影响线识别是移动荷载下既有结构评估的理论基础[2],已被广泛地应用于结构损伤演化[3−6]、结构模型修正[7−9]、桥梁动态称重[10−12]等方面。影响线识别方法主要分为两类[2]:空间域方法和频率域方法。在空间域方法中,OBRIEN 等[13]基于最小二乘法求解影响线函数的有限散点;YAMAGUCHI 等[14]在引入多项式函数来描述影响线的基础上求解影响线函数;王宁波等[15]考虑多项式分段函数与桥梁动力效应消除;IENG[16]采用极大似然估计;陈志为等[17]结合正则化方法和三次B 样条曲线方法,并在实验室钢筋混凝土桥梁试验中验证方法;ZHENG 等[18]提出正则化最小平方QR 分解法;KHUC 和CATBAS[19]针对桥梁横向效应较大的宽桥提出基于迭代逼近进行影响面识别;ZHENG等[20]提出基于经验模态分解的桥梁静影响线识别方法;朱前坤等[21]基于计算机视觉识别人行桥挠度影响线;ZHOU 等[22]提出大数据和仿射区间分析方法;ZHENG 等[23]基于节点编码重排将二维影响面识别转化为一维影响线识别。在频率域方法中,HUNT[24]提出通过消除多轴效应来提取桥梁影响线的方法;FRØSETH 等[25]提出频域正则化滤波器进行影响线提取;YAN 等[26]提出静力响应传递比函数法。
结构影响线识别本质上是基于系统输入-输出含噪数据反向对静力系统指定截面的响应函数进行识别。已有研究虽然取得了进展,但它们在以下两个方面存在局限性:1) 缺乏反问题可识别性分析;2) 缺乏不确定性量化。反问题可识别性分析是为了厘清系统识别的参数的解的情况。对于一般情况下未知函数形式的待识别影响线,其对应的参数向量的维度是无穷。由于无穷维参数是不可识别的,已有的识别方法的模型参数化形式可分成两类:第一类是直接参数化,参数是加载位置对应的影响值[13,16,18];第二类是间接参数化,参数是选定位置对应的影响值[14−15,17,19]。无论是哪一种参数化形式,严格地进行反问题可识别性分析都是影响线识别的前提。不确定性量化是基于测量输入-输出含噪数据估计影响线参数的后验概率密度函数。已有识别方法一般是给出参数最优值估计。然而,实际工程通常伴随着显著的不确定性源(测量信息不完备、测量误差、模型误差、未知干扰等),导致工程反问题的解同样伴随着显著的不确定性。忽略这些不确定性将导致结构响应预测与评估的可靠性降低。
针对上述两个局限性,本文在贝叶斯概率框架的基础上开展关于影响线识别的反问题可识别性分析与贝叶斯不确定性量化。贝叶斯概率是基于贝叶斯理论表征观测者对未知命题的置信度[27]。在工程力学系统识别领域,BECK 与KATAFYGIOTIS是建立贝叶斯概率框架的先驱者[28−33]。该概率框架被不断发展并应用于不同问题,包括可靠度问题[34−35]、模态参数更新问题[36−37]、有限元模型修正[38−39]、系统模型选择[40−41]等。
反问题可识别性分析(Model Identifiability)这一概念最初是由BECK 与KATAFYGIOTIS[28]提出。可识别性分析的对象是参数最优值,可识别性分析的定量指标是参数最优值的唯一性。反问题可识别性分析可建立在参数最大似然估计值的基础上进行。该分析将模型可识别性分成全局模型可识别、局部模型可识别、模型不可识别三种情况。只有在全局模型可识别的前提下,反问题存在唯一解。贝叶斯不确定性量化是基于参数后验概率密度函数。首先,本文进行基于直接参数化的影响线识别,包括系统输入与输出构造、反问题可识别性分析、参数最优值。经分析得出:一方面,直接参数化无法保证全局模型可识别;另一方面,现有方法即使是全局模型可识别的情况下也无法进行不确定性量化。然后,为保证反问题是全局模型可识别且同时获取参数后验概率密度函数,本文提出基于降维贝叶斯不确定性量化的影响线后验识别,包括系统输入与输出重构、反问题可识别性分析、后验概率密度函数。最后,本文进行新光大桥吊杆拉力影响线识别与简支梁桥应变影响线识别,并验证提出方法的有效性。
1 基于直接参数化的影响线识别
1.1 系统输入与输出构造


基于上述公式进行参数求解的前提是厘清参数的解的情况。桥梁影响线识别是一个反问题。该反问题在某些情况下是病态的(例如,参数的解有无穷多个)。病态反问题的求解结果是无法用于实际工程的。因此,在影响线识别之前,需要进行严格的反问题可识别性分析。
1.2 反问题可识别性分析



1.3 参数最优值
在全局模型可识别的情况下(情况3),反问题存在唯一解。通过考虑∂lnp(Φ|W,L)/∂ϕ=0,参数最优值:
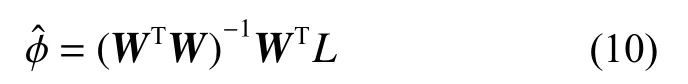
上述这种仅通过目标函数进行参数最优值估计的做法,是已有方法的普遍做法。然而,实际工程通常伴随着显著的不确定性源(测量信息不完备、测量误差、模型误差、未知干扰等),导致工程反问题的解同样伴随着显著的不确定性。忽略这些不确定性将导致结构评估与预测的可靠性降低。
为保证反问题是全局模型可识别且获取参数后验概率密度函数,本文在下一节提出基于降维贝叶斯不确定性量化的影响线后验识别,包括降维参数化与基于贝叶斯定理的参数后验概率密度函数。
2 基于降维贝叶斯不确定性量化的影响线后验识别
2.1 基于降维参数化的系统输入与输出重构
降维参数化是间接参数化的一种,其目的在于引入不直接取决于数据测量方案的参数化形式,从而降低参数维度,提高全局模型可识别的可能性。



下面将对比直接参数化与降维参数化的反问题可识别性。
2.2 反问题可识别性分析



3 新光大桥吊杆拉力影响线识别
本节应用提出的降维贝叶斯估计进行新光大桥吊杆拉力影响线识别。为了检验提出方法的有效性,首先,介绍系统输入与输出数据;然后,对比不同工况(不同数据与降维模型)的影响线识别效果;最后,对比不同降维互异位置向量(受“影响线参数位置间隔长度”控制,下文会具体描述)的影响线识别效果。
新光大桥是广州市内跨越珠江主航道的一座特大型桥梁,该桥采用三角刚架与下承式无铰系杆拱相结合的结构体系,为一座总跨径S=782 m的三跨连续刚构中承式拱桥,其跨径组合为177 m+428 m+177 m(图1(a))[43]。吊杆是新光大桥的重要受力构件,其主要承受桥面系传来的竖向荷载。该桥共设置6 条车道,包括3 条上行车道和3 条下行车道,车道布置如图1(b)所示。

图1 新光大桥概况 /m Fig. 1 Overview of the Xinguang Bridge
系统输入与输出数据是车辆荷载与含噪荷载效应。车辆荷载以模拟车队的形式进行加载[44]。车队代表车型采用《公路桥涵设计通用规范》[45]的五轴车:其前轴至后轴的轴距分别为3 m、1.4 m、7 m、1.4 m,第一轴至第五轴的轴重分别为30 kN、120 kN、120 kN、140 kN、140 kN(总重550 kN)。车队交通流考虑车队车辆数Q(单位:辆)和时变车间距d(后车与前车的距离,单位:m)。其中代表车型、Q、d都可根据实际情况进行调整。为了检验提出方法在不同车辆荷载下的影响线识别效果,车流数Q取Q20 与Q80 两种情况,分别对应20 辆车与80 辆车;随机车间距d考虑d80 与d100 两者情况,分别对应均值为80 m 与100 m、标准差都为1 的高斯分布,因此,一共有Q20-d80、Q20-d100、Q80-d80、Q80-d100 这4 种车辆荷载情况。荷载效应选取C1 车道(图1(b))对应的主跨跨中吊杆(见图1(a)中5#)拉力。荷载效应数据通过将上述车队加载到主跨跨中吊杆对应C1 车道的影响线获取。荷载效应采样开始于车队首辆车进入桥梁,采样间隔为车队首辆车每前进10 m,采样结束于车队末辆车离开桥梁。含噪声的荷载效应获取如下:基于车辆荷载与影响线获得未含噪声的荷载效应,在此基础上叠加噪声获得含噪声的荷载效应。噪声通过随机采样获取,其服从独立高斯分布:均值为0,标准差为未含噪声的荷载效应数据集标准差的5%(对应的是5%的噪声水平)。
通过考虑两种降维模型(2.1 的第1 降维模型(m1)与第2 降维模型(m2))与4 种数据(Q20-d80、Q20-d100、Q80-d80、Q80-d100)与的组合,获得8 种工况(m1-Q20-d80、m1-Q20-d100、m1-Q80-d80、m1-Q80-d100、m2-Q20-d80、m2-Q20-d100、m2-Q80-d80、m2-Q80-d100),并对比它们的影响线识别效果。两种降维模型基于同样的降维互异位置向量X:X={xi|xi=∆x.i,i=0,1,···,floor,xceil=S,floor=⎿S/∆x」,ceil=「S/∆x⏋},其中 ⎿.」 与 「.⏋分别是向下与向上取整函数, ∆x为影响线参数位置间隔长度(单位:m),此处设∆x=10。
表1 汇总了车辆荷载工况与降维贝叶斯方法参数工况。图2 展示了不同工况的识别影响线后验最优值与后验95%置信区间。需要说明的是,后验95%置信区间是基于后验(p+1)维的高斯分布G(mΘˆ,mΣˆ)得出。该图同时展示了实际影响线用于识别值与实际值的对比。图2(a)和图2(c)分别展示了第1 和第2 降维模型的后验最优值;图2(b)和图2(d) 分别展示了第1 和第2 降维模型的后验95%置信区间。结果表明:1)本文提出的两个降维模型的影响线最优值与不确定性量化结果均能满足实际结构影响线识别;2)第2 降维模型比第1 降维模型更优—它能获取更准确的函数峰值区域后验估计值与给出更小的后验置信区间。图3给出了不同工况的识别影响线识别残差绝对值与标准差的箱线图。箱线图从上到下五条线依次是:最大值、四分之三等分点、二分之一等分点(中位数)、四分之一等分点、最小值。其中,图3(a)残差绝对值箱线图是基于图2(a)与图2(c);图3(b)标准差箱线图是基于图2(b)与图2(d)。结果表明:1)对于同一个降维模型,交通流Q和车辆间距d增大,残差绝对值与标准差两者的中位数与波动范围会相应降小;2)第2 降维模型比第1 降维模型更优—这与图2 的结论一致。上述结果背后的原因是:在[0,300]与(482,782]的区域,真实影响线几乎为0,该段区域两个降维模型的结果类似;在[300,482]的区域,真实影响线非常陡峭,第1 降维模型假设 ∆x内影响线为常数限制了其表现、而第2 降维模型假设 ∆x内影响线为直线满足要求。在一般情况下,如果存在多个降维模型,拥有更多参数的降维模型由于解的空间更大,所以它能更好地拟合影响线数据。

图2 不同工况的识别影响线后验最优值与后验95%置信区间Fig. 2 Posterior optimal values and 95% confidence intervals of identified influence lines of different cases
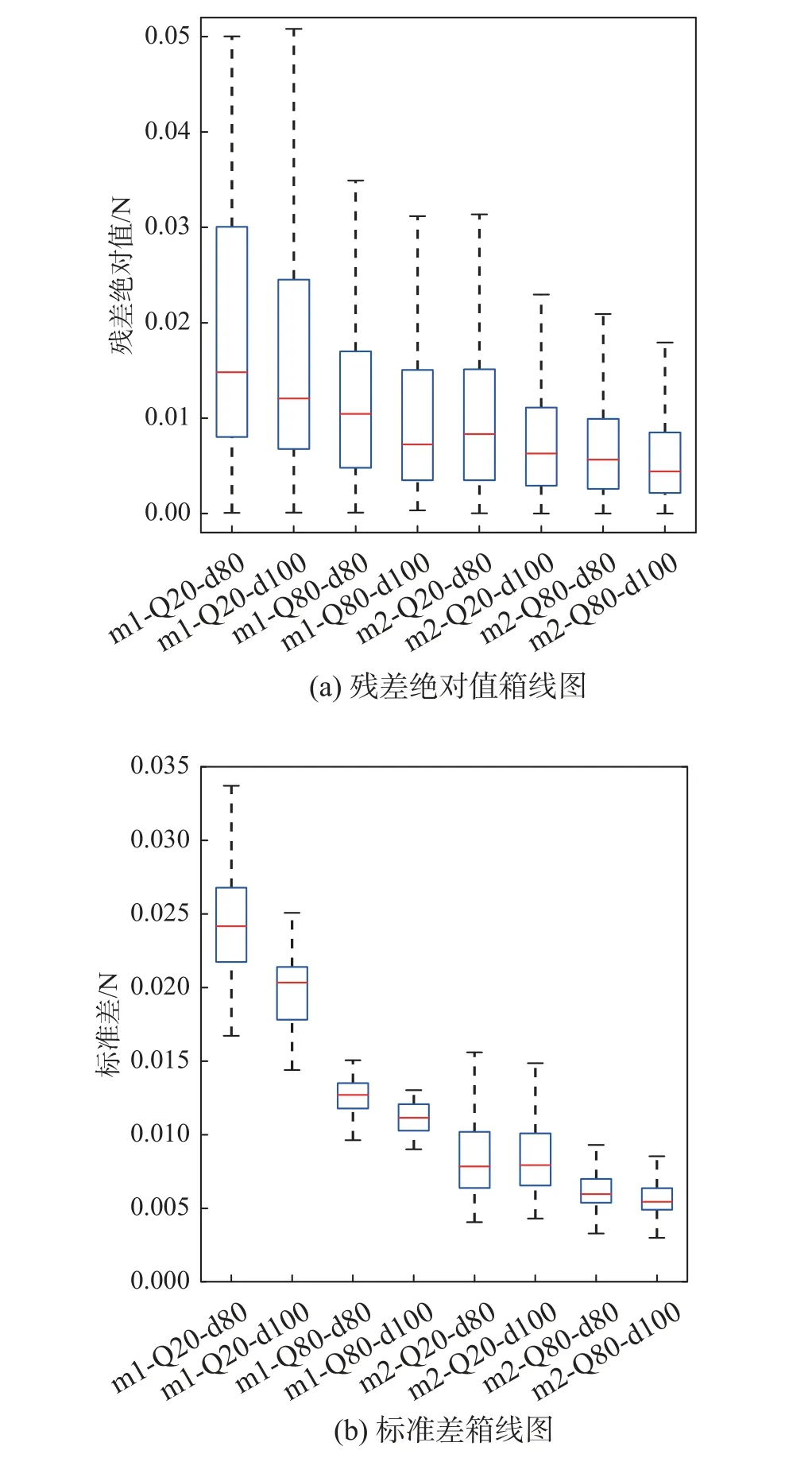
图3 不同工况下识别影响线的残差绝对值与标准差箱线图Fig. 3 Box plots of absolute values of residuals and standard deviations of identified influence lines of different cases

表1 车辆荷载工况与降维贝叶斯方法参数工况Table 1 Different cases of vehicle loads and parameters of reduced-dimension Bayesian uncertainty quantification
为了对比不同降维互异位置向量的影响线识别效果,对m2-Q20-d80 工况考虑不同的∆x={5,10,20,40,80}。图4 展示了m2-Q20-d80 工况下不同参数位置间隔长度的识别影响线的残差绝对值与标准差箱线图。可以看出:1) ∆x从10 减小到5,识别效果变差;2) ∆x从10 增加到80,识别效果变差。以下对上述结果进行解释:一方面,∆x减小,参数数目增加,但每个 ∆x内的荷载样本量减少—等价于参数识别的数据信息减少;另一方面, ∆x增加,参数数目降低—等价于参数解空间的维度降低。因此, ∆x的选择区间不宜过大或过小。在此工况下, ∆x的合适选择区间是[10,20]。此区间内,降维贝叶斯的影响线识别结果能兼顾稳定性与准确性。一般情况下,建议以桥梁最小跨径的5%~10%为 ∆x的初始选择,通过减小或增加 ∆x,观测识别结果的变化,最终结合工程判断进行选取。

图4 m2-Q20-d80 工况下不同参数位置间隔长度的识别影响线的残差绝对值与标准差箱线图Fig. 4 Box plots of absolute values of residuals and standard deviations of identified influence lines by different interval lengths of position of parameter under the case of m2-Q20-D80
4 简支梁桥应变影响线识别
本节基于简支梁桥实测数据[2,17]与模拟数据,对应变影响线进行识别。该简支梁试验桥梁跨径为25 m,采用等截面形式,截面弹性模量EI=9.3×107kN·m2,应变计安装于跨中。加载车辆为四轴车辆,第2~4 轴与第1 轴的距离分别为1.95 m、6.20 m 和7.60 m,第1~4 轴的轴重分别为11.9 t、11.9 t、23.9 t 和23.9 t。卡车的位置由安装在加载车辆前轴上方的GPS 传感器采集,车辆行驶速度为1 m/s,采样频率为10 Hz。实测输入数据来自于车辆轴重与定位GPS 传感器。实测输出数据来自于跨中应变计采集数据集。模拟输出数据来自于未含噪声的模拟应变叠加噪声,其中:未含噪声的模拟应变通过实测输入数据下进行跨中应变理论影响线加载获得;噪声通过随机采样获取,其服从独立高斯分布:均值为0,标准差为未含噪声的荷载效应数据集标准差的5%(对应的是5%的噪声水平)。
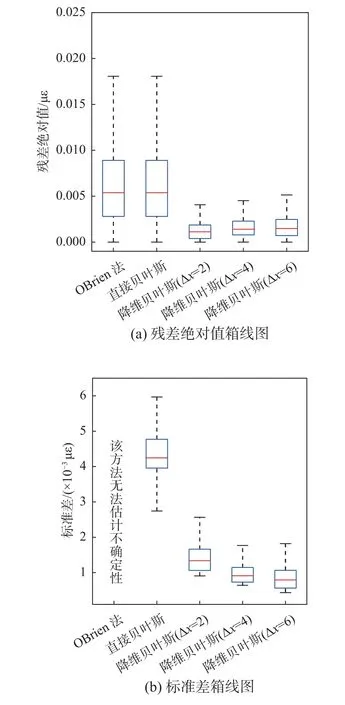
本文对比了三种方法:1) OBrien 提出的最小二乘法[13](记为:OBrien 法);2)基于直接参数化的贝叶斯方法[16](记为:直接贝叶斯);3) 本文提出的降维贝叶斯方法(记为:降维贝叶斯)。其中,OBrien 法形式与式(10)等价;直接贝叶斯仅考虑第1 小节的直接参数化(也就是,不考虑2.1 小节的参数降维),在式(5)的基础上直接引入贝叶斯概率框架,获取非降维参数的后验概率密度函数:其服从于一个h维的高斯分布—其均值与OBrien 法获得的最优参数一致、其协方差矩阵为Fisher Information 矩阵。降维贝叶斯采用第2 降维模型(m2),其背后原因是跨中应变影响线理论上为折线。需要注意的是:1) 前两者方法对应的参数维度是h,而本文提出的降维贝叶斯对应的降维参数维度是p(p 图5 展示了实测数据和模拟数据下三种方法的识别影响线。图5(a)展示了跨中应变实测数据和模拟数据,其中,横轴表示加载车辆第1 轴位置;图5(b)、图5(c)和图5(d)分别是OBrien 法、直接贝叶斯和降维贝叶斯(∆x=4)对应的影响线识别结果。结果表明:1)影响线最优值方面,相对于OBrien 法和直接贝叶斯,降维贝叶斯的结果更准确且更平滑;2)影响线不确定性量化方面,OBrien 法无法给出置信区间、直接贝叶斯可以给出置信区间、降维贝叶斯的置信区间更平滑。这些结果均表明,参数降维与贝叶斯不确定性量化是改善影响线识别效果的两个重要因素;3)模拟数据与实测数据对应的影响线识别结果存在差异,这一点结论与论文[2,17]一致。通常情况下,实测过程中会存在许多未知的不确定性源,这更表明需要引入贝叶斯概率框架对影响线识别结果进行不确定性量化。 图5 实测数据和模拟数据下三种方法的识别影响线Fig. 5 Identified influence lines by three different methods using measured and simulated datasets 图6 展示了模拟数据下三种方法的识别影响线的残差绝对值与标准差箱线图。同时,为讨论参数 ∆x(即:影响线参数位置间隔长度)取值对降维贝叶斯的影响,本文对降维贝叶斯考虑三种参数工况: ∆x=2,4,6。可以看出:1)对于图6(a)残差绝对值箱线图,一方面,OBrien 法与直接贝叶斯一致—这是因为它们两者都是基于同样的直接参数化,因此两者的最优值与残差都一致;另一方面,不同工况下降维贝叶斯的残差各分位数结果更低,比前两种方法都好;2)对于图6(b)标准差箱线图,OBrien 法无法估计不确定性;直接贝叶斯可以估计标准差;不同工况下降维贝叶斯的标准差各分位数更低,比直接贝叶斯更好;3)影响线参数位置间隔长度的选取在合理范围内,降维贝叶斯的影响线识别结果能兼顾稳定性与准确性。 图6 模拟数据下三种方法的识别影响线的残差绝对值与标准差箱线图Fig. 6 Box plots of absolute values of residuals and standard deviations of identified influence lines by three different methods using simulated datasets 本文在贝叶斯概率框架的基础上开展关于影响线识别的反问题可识别性分析与贝叶斯不确定性量化。反问题可识别性分析是建立在均匀先验的参数后验最优值的基础上将模型可识别性分成全局模型可识别、局部模型可识别、模型不可识别三种情况。只有在全局模型可识别的前提下,反问题存在唯一解。为保证反问题是全局模型可识别且同时获取参数后验概率密度函数,本文提出基于降维贝叶斯不确定性量化的影响线后验识别。本文的主要结论如下: (1)直接参数化无法保证全局模型可识别;现有方法即使是全局模型可识别的情况下也无法进行不确定性量化。 (2)降维参数化可保证反问题是全局模型可识别的;可基于贝叶斯定理获得参数后验概率密度函数。参数降维与贝叶斯不确定性量化是改善影响线识别效果的两个重要因素。 (3)如果存在多个降维模型,拥有更多参数的降维模型由于解的空间更大,因此能更好地拟合影响线数据。影响线参数位置间隔长度的选取在合理范围内,降维贝叶斯的影响线识别结果能兼顾稳定性与准确性。一般情况下,建议以桥梁最小跨径的5%~10%为间隔长度的初始选择,通过减小或增加间隔长度,观测识别结果的变化,最终结合工程判断进行选取。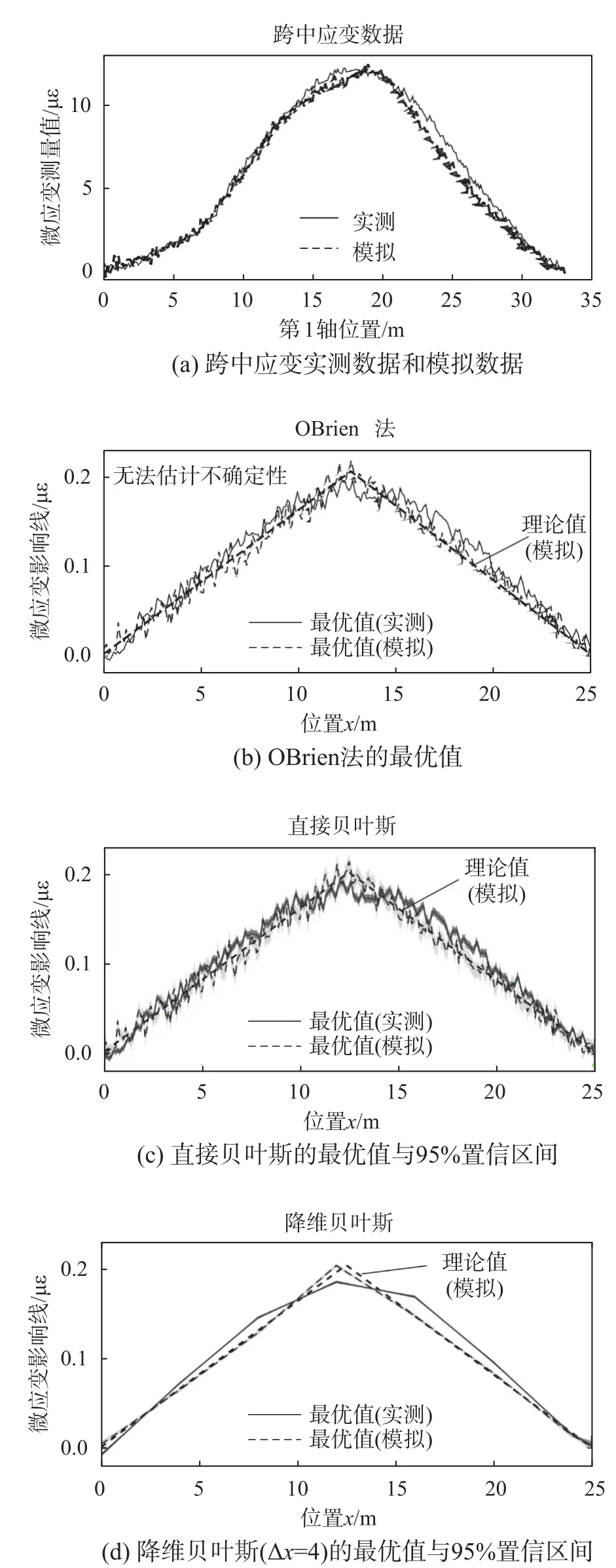
5 结论
