一种基于折扣因子D的贝叶斯方法在MRCT中的应用研究*

佟 亮 蒋志伟 李 晨 李 凡 葛 伟 胡海霞 王 陵△ 夏结来△

【提 要】 目的 在折扣因子D的基础上，提出一种新的贝叶斯方法用于评价多区域临床试验中目标区药物的疗效，并探讨本方法的可行性。方法 以Ⅱ期临床试验中收集到目标药物的种族信息作为样本信息，类似药物或同类药物的临床试验收集到的种族信息作为先验信息，构建折扣因子D的后验分布，并进一步计算加权Z检验统计量ZW的后验分布，比较先验分布分别为无信息先验、共轭先验和分层先验时D后验分布的特点，并比较不同类型D的后验分布对试验检验效能的影响。结果 当历史信息的信息量相对样本信息很小时，则后验均值主要由样本信息决定，后验分布的信息量基本接近样本信息的量，当历史信息的量逐渐增大时，后验均值逐渐向历史信息均值靠拢，后验分布的信息量也逐渐增大。检验效能由D的后验均值决定，与D的变异程度无关。结论 本研究提出的贝叶斯方法可以较好地模拟实际情况，具有良好的实际意义和可操作性。

某药物在国外注册上市后，由于种族差异对药物有效性和安全性的潜在影响，并不能直接在国内注册上市。若忽略该药物在国外积累的临床试验资料则需要在国内完整重复整个药物研发过程，不仅会造成大量的资源浪费，而且会使国内患者不能及时得到有效药物的治疗[1-2]。多区域临床试验(multi-regional clinical trial，MRCT)是目前解决上述问题的主要方法，即全球各个国家或地区在同一个临床试验方案的指导下，同步进行临床试验，试验结束后可同时对各国家或地区的药物疗效和安全性作出评价，达到同期注册上市的目的。然而考虑到MRCT中各参与国家或地区的种族差异问题，MRCT整体得出有效结论后如何将MRCT的结果推广至各参与国家或地区，尚缺乏权威、公认的统计学方法，各参与国家或地区的审评机构对MRCT的接受程度和审批要求也不尽相同。国内外生物统计学家就上述问题提出了不同的方法[3-6]。

鉴于上述问题，本研究拟采用贝叶斯方法，赋予D更具体的实际意义，拟合Ⅲ期临床试验前积累的种族信息，构建相对客观的D后验分布，并同时体现其集中趋势和离散趋势，进一步评价TE区药物疗效。结合公式推导和Monte Carlo模拟，研究不同D的先验分布对其后验分布的影响以及不同D的后验分布对试验检验效能的影响，探讨该方法的可行性。

材料与方法

1.试验设计

假定MRCT阶段的样本量为NMRCT，其中包括NNTE个NTE受试者，NTEM个TE受试者，LCT阶段包括NTEL个TE受试者。D的原定义是NNTE个NTE受试者可打折成D×NNTE个TE受试者进行了试验。本研究在Wang的基础上赋予D更具体的实际意义：假定部分NTE区受试者和TE区受试者种族相似程度高，这部分受试者可直接视为目标区受试者进行了试验，该部分受试者所占的比例为D，其它NTE区受试者和TE区受试者种族相似程度低，这部分受试者不能提供信息给TE区受试者，其所占比例为1-D。则D的定义可转换为在虚拟实验中，NTE区的受试者相当于TE区受试者进行了试验的比例，在这种定义下，NNTE个NTE受试者仍可打折成D×NNTE个TE受试者进行了试验。如此估计D就转换为估计在虚拟试验中NTE区某个受试者是否可以等价于TE区的受试者进行了试验，可以从个体的角度来评价种族相似性。基于这种实际意义，本研究通过贝叶斯方法拟合样本信息和历史信息，在Ⅲ期临床试验开展前构建D的后验分布，得到Ⅲ期临床试验数据后构建ZW的后验分布。若P(ZW>1.96)>C，则认为目标区的药物有效，C为某预先设定的界值。

2.构建D的后验分布

(1)样本信息

由于Ⅲ期临床试验的目的主要是评价药物的疗效，对不同区域受试者的种族方面信息收集较少，且D应在Ⅲ期临床试验前确定，而Ⅱ期临床试验会对受试者进行药代动力学和药效动力学研究，对受试者的种族信息研究相对深入，故本研究提出可在原有Ⅱ期临床试验基础上，更进一步收集Ⅱ期临床试验受试者的种族信息，成立专家组，评定N个NTE区受试者中，可视为TE区受试者的人数X，以此可构建D的似然函数：

(2)历史信息

本研究中以已完成的与目标药物类似或相同种类的药物临床试验所积累的种族信息作为先验信息，先验分布可分为以下三种情况。

①无信息先验

本研究中的似然函数形式，不能直接确定无信息先验。采用Jeffreys提出的方法[16]，用Fisher信息阵行列式的平方根作为D的无信息先验。求解步骤如下：

参数的对数似然函数

a.Fisher信息阵

b.D的无信息先验密度

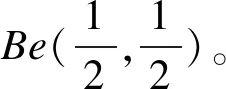
事实上，先验分布并不是唯一的，当先验分布取Be(1，1)，即取0～1之间的均匀分布时，对结果的影响也不大。

②共轭先验分布

假定D的先验分布为π(D)～Be(α，β)，则后验分布为：

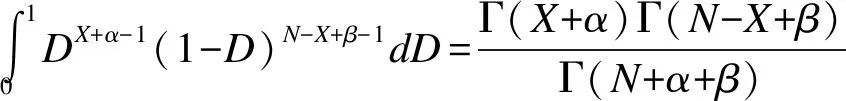
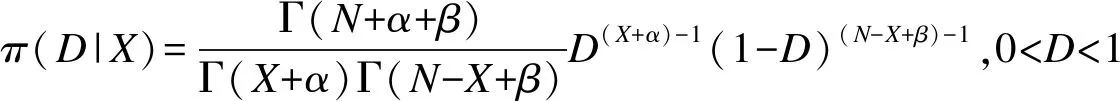
由此可知，当先验分布取贝塔分布时，D的后验分布仍为贝塔分布，故D的共轭先验密度形式为Be(α，β)。

假定在类似或同类药物的临床试验中，收集到较全面的种族信息的NTE区受试者例数为N0，其中可视为TE区受试者的例数为X0，则构建的共轭先验中α=X0，β=N0-X0。

③分层先验

在利用类似或同类的药物所积累的种族信息数据构建共轭先验时，经专家评定，NTE区受试者可视为TE区受试者的例数X0可能不是一固定的值，而是在某个范围内以某种形式分布。故我们引入贝叶斯层次模型，赋予α一先验分布，即超先验，则先验分布由原来的贝塔分布形式的共轭先验变成了分层先验。

(3)拟合D的后验分布

①无信息先验和共轭先验时的后验分布

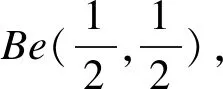
②分层先验时的后验分布

由于采用分层先验时，先验分布的函数形式比较复杂，积分计算困难，难以得到后验分布的函数形式，故利用马尔科夫链蒙特卡洛(markov chain monte carlo，MCMC)方法进行模拟得出采用分层先验时D的后验分布。在本部分中，我们用α代表对历史信息的不确定性，α的均值相同，波动范围越大，对历史信息就越不确定。先验分布取Be(α，40-α)，其中α按α=12、α～uniform(10，14)、α～uniform(8，16)、α～uniform(6，18)四种情况进行模拟。Ⅱ期临床试验中N=40，X=20。比较α取不同超先验时，对后验分布的影响。

利用SAS 9.4 MCMC过程步模拟生成分层先验时D的后验分布的流程如图1所示：

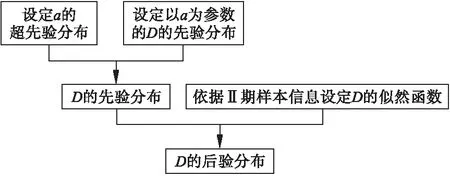
图1 分层先验条件下的后验分布生成流程图

3.D的后验分布对检验效能的影响

参数设置：当先验信息为无信息先验或共轭先验时，D的后验分布仍为贝塔分布Be(a，b)；当先验信息取分层先验时，D的后验分布难以用具体的函数形式表示，可通过MCMC模拟得出。本部分取NMRCT=500，NNTE=400，NTEM=100，NTEL=46，C=0.5、0.6。分以下几种情况模拟：

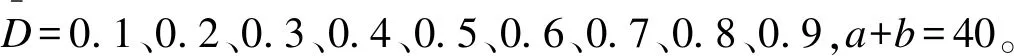
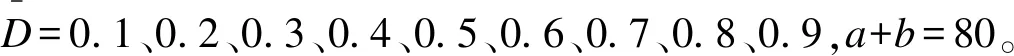
情况3：分层先验的后验分布：

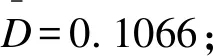
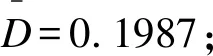
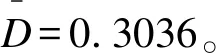
情况4：采用经典频率学派方法，若ZW>1.96，则判定目标药物有效，D=0.1、0.2、0.3、0.4、0.5、0.6、0.7、0.8、0.9。

模拟流程图如图2所示：

其中SZNTE、SZTE为NTE区和TE区Z检验统计量的样本值，ZNTE、ZTE为NTE区和TE区Z检验统计量的总体值。

结 果

1.无信息先验和不同形式的贝塔先验对D后验分布的影响

当取无信息先验时，后验均值为0.5，后验方差为0.002451，这与样本信息中D的均值和方差基本是一致的。

以N0为横轴，后验均值和后验方差为纵轴，绘制散点图后发现，当N0比较小时，D的后验均值接近于0.5，即样本信息的均值，随着N0逐渐增大，D的后验均值逐渐向0.3靠拢，即逐渐接近历史信息的均值。当N0=N=100时，后验均值=0.4，为样本信息和历史信息的均值。随着N0增大，D后验方差逐渐减小,见图3。

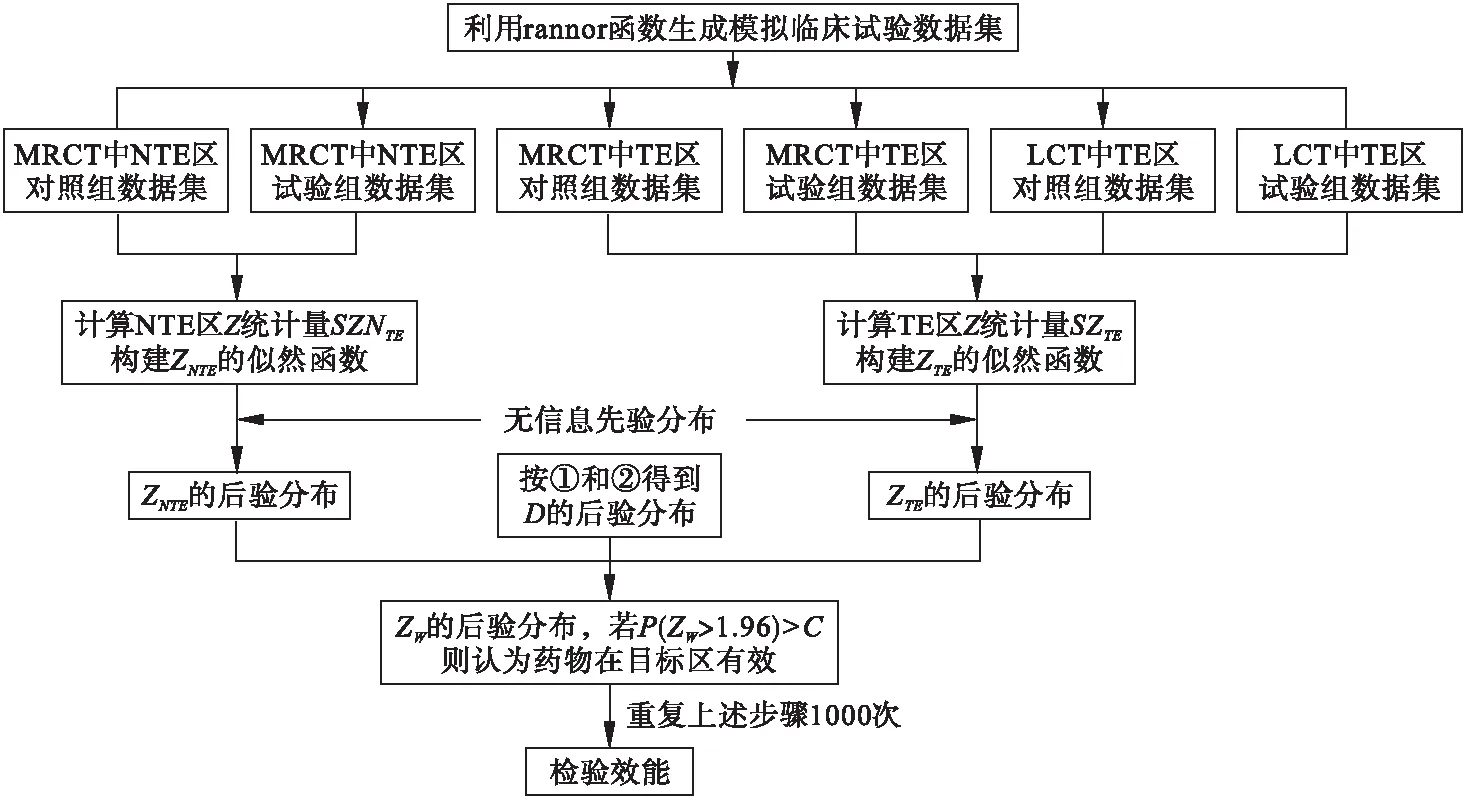
图2 检验效能计算流程图

图3 不同形式的贝塔先验对后验均值的影响

2.不同形式的分层先验对D后验分布的影响

随着α波动范围逐渐增大时，先验均值基本不变，先验标准差逐渐增大，后验均值逐渐向样本均值0.5靠拢，后验标准差逐渐增大，见表1。

表1 不同形式的分层先验对后验均值和方差的影响

3.不同D的后验分布对试验检验效能的影响

当C取值相同时，情况1、情况2、情况3中检验效能随后验均值变化的曲线基本重合，检验效能均随后验均值增大并逐渐趋于平稳。相同的后验均值条件下，检验效能在C=0.6相对C=0.5时相对较低。情况4为采用经典频率学派计算检验效能，C=0.5时，情况1、情况2、情况3和情况4的曲线基本重合，见图4。

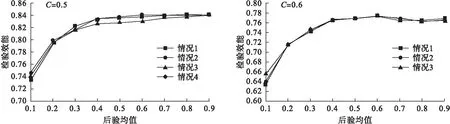
图4 不同后验分布的后验均值对检验效能的影响

讨 论

本研究在Wang提出折扣因子D的基础上赋予D更具体的实际意义，进一步提出了一种MRCT中评价TE区药物疗效的贝叶斯方法，并结合公式推导和Monte Carlo模拟研究了不同D的先验分布对其后验分布的影响以及不同D的后验分布对试验检验效能的影响，探讨了该方法的可行性。

在本研究中，N0、N的大小分别表示历史信息和样本信息信息量的大小，收集到的受试者例数越多，表明收集到的种族信息越全面，信息量越大。在模型上先验分布、似然函数和后验分布的标准差代表信息量的大小，标准差越小，表明对D的分布范围越确定，信息量越大。当α取一定范围内的均匀分布时，代表研究者对前期收集到的种族信息不太确定，信息量小，且均匀分布波动范围越大，信息量越小，用分层先验拟合这种情况时，正好体现了这一结果。综合结果可以看出，当历史信息的信息量相对样本信息很小时，则后验均值主要由样本信息决定，后验分布的信息量基本接近样本信息的量，当历史信息的量逐渐增大时，后验均值逐渐向历史信息均值靠拢，后验分布的信息量也逐渐增大，模型可以较好地模拟实际情况。

本方法中，用情况1、情况2、情况3可以不失一般性地代表D可能出现的所有后验分布情况。本研究提出的贝叶斯方法中D的后验均值即对应原频率学派方法[13]中的D值，而D的后验标准差则可反映D的变异程度，由结果可以看出：试验的检验效能主要受D后验均值或D值影响，而与D的变异程度关系不大，即只要D的后验均值固定，无论收集到多少受试者评价D都对检验效能没有影响，但是在构建后验分布时，应尽可能全面地收集样本信息和历史信息，收集信息的多少虽然不能直接影响检验效能，但是可能会影响后验均值估计的准确性，即如果收集信息过少，可能会导致D后验均值估计不准确。本研究提出的贝叶斯方法较原频率学派方法[13]的优势在于可将D的变异程度纳入考虑，假定两种不同的情况：一种情况是没有收集到任何有用信息来评价D，D的后验分布为Be(1，1)，另一种情况是假定收集到100名NTE区受试者的详细种族相关信息，其中50名可等价于TE区受试者进行了试验，D的后验分布为Be(100，100)，虽然两种假定情况下D的后验均值均为0.5，但是第二种假定情况把握更大，D的变异更小，对应更大的检验效能较为合理。若采用原频率学派方法[13]，不考虑D的变异，两种假定情况D均为0.5，检验效能相同，不符合实际情况，而本研究提出的贝叶斯方法则为考虑D的变异对检验效能的影响提供了基础，可在本研究提出的贝叶斯方法基础上进一步利用D的后验标准差对ZW进行调整，从而使D的变异程度较大时对应较小的检验效能。

本研究提出了一种根据Ⅱ期临床试验种族信息和历史种族信息确定折扣因子D，并进一步评价TE区药物疗效的贝叶斯方法。本方法允许研究者从生物个体的角度对种族差异作出评定，对种族差异的评价更加客观，并且既能体现D的集中趋势，又能体现D的离散趋势，具有良好的实际意义。不足之处在于没有给出一个NTE区受试者可以等价于一个TE区受试者的量化标准，本研究建议主要通过药代动力学、药效动力学和疗效数据进行判断，兼顾可能导致区域间药物疗效差异的其他因素，这将会在以后的工作中结合实践予以补充。