聚脲材料动态压缩力学行为的数值模拟研究

孙 妮，柳锦春，王钰颖

(南京航空航天大学土木与机场工程系，南京 211106)

近些年来，恐怖主义袭击频率不断提高，大规模工业爆炸频有发生，对现有防护结构提出了严峻的挑战[1]。研究发现，爆炸事故中的民众伤亡大多来自爆炸所致的玻璃、门窗、墙体等碎片的飞溅伤害，即二次破片伤害。为了保障人民的生命财产安全，可以通过在已有防护结构表面涂覆弹性体材料来加固已有防护结构，减少碎片的飞溅伤害[2]。为此，国内外研究者们致力于开发和研究新的抗冲击性能良好的材料来加固已有防护结构，聚脲弹性体材料由于其在抗冲击和爆炸防护方面具有的优异性能而在此过程中脱颖而出。

为了研究聚脲材料的抗冲击防爆性能，国内外众多学者开展了聚脲材料的静动态压缩、拉伸力学性能试验和本构方程拟合。国外研究者率先对聚脲弹性体材料进行了力学性能研究，麻省理工学院的YI 等[3]、SARVA 等[4]率先开展了聚脲材料的准静态和动态压缩试验，随后，麻省理工学院的SHIM 等[5]补充了聚脲弹性体材料在中等应变率下的压缩试验，美国海军研究实验室的PATHAK 等[6]和墨尔本大学的RAMAN 等[7]展开了聚脲弹性体在中低应变率下的拉伸试验。随后，国内研究者也逐渐开展了聚脲防爆材料的力学性能的研究，甘云丹[8]、蔡桂杰[9]、许帅[10]、戴平仁[11]等分别对聚脲材料进行了不同应变率下的压缩和拉伸试验。综合以上研究者对聚脲弹性体材料进行的静、动态力学性能试验研究表明，聚脲材料具有非常优异的力学特性，在拉伸和压缩加载条件下的应力-应变关系呈现出非线性和极强的应变率相关性，而且在中低应变率下具有拉压一致性。

聚脲材料复杂的力学行为极大地加大了建立精确聚脲本构关系模型的难度，众多研究者提出了不同的参数化本构模型，主要有超弹性本构模型、粘弹性本构模型和粘性-超弹性模型，这些模型形式复杂、参数众多，很难应用于爆炸冲击荷载作用下加固防护结构的有限元模型中。目前，ANSYS/LS-DYNA 显式非线性动力分析程序被广泛应用于爆炸与冲击问题，但是DYNA 材料数据库中还没有成熟的聚脲材料模型。因此，本文提出考虑动弹性模量、动态强度因子和动态切线模量来研究聚脲材料的动态压缩力学特性，根据得到的压缩力学特性，基于DYNA 中已有的材料模型，提出聚脲材料考虑应变速率效应的三段式弹塑性简化本构模型，建立不同应变率下聚脲材料的压缩有限元模型，对聚脲防爆材料的力学行为进行数值模拟分析来验证模型的有效性，为聚脲涂覆加固防护结构有限元模型提供材料依据。

1 聚脲材料动态压缩力学特性

1.1 静、动态应力-应变曲线

汇总众多研究者对聚脲材料力学行为的试验，研究分析聚脲材料的力学行为特性，发现不同研究者得到的应力-应变曲线趋势具有较好的一致性。现选取WANG 等[12]在低中高不同应变率下通过压缩试验得到的应力-应变关系作为聚脲材料静动态压缩荷载下的典型应力-应变关系进行分析，如图1 所示。

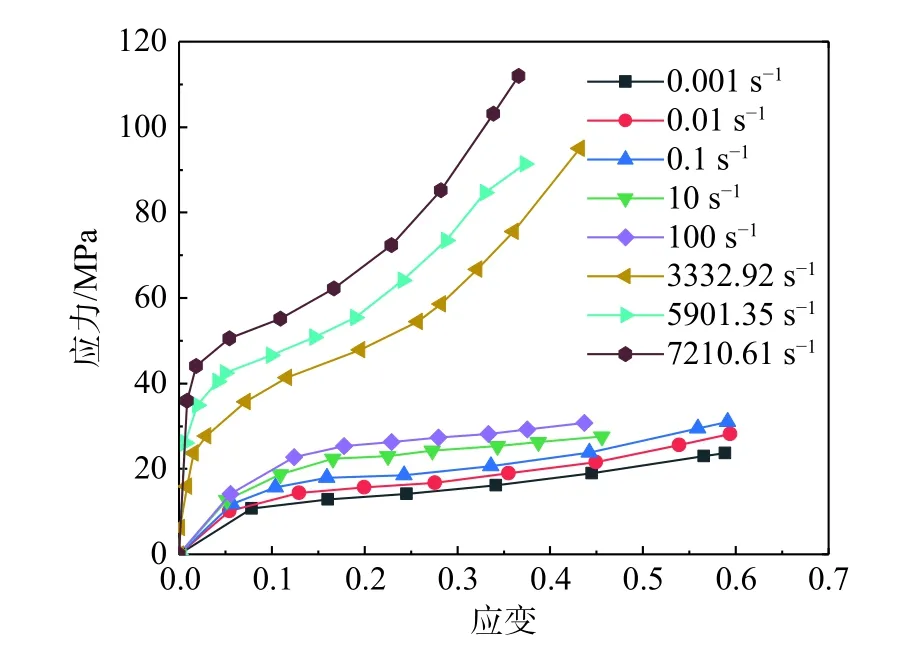
图1 WANG 等[12]通过压缩试验所得应力-应变曲线Fig. 1 Stress-strain curve obtained by compression test of WANG[12]

从图1 中可以看到，聚脲材料在某一应变率下的真实力学行为可以大致分为3 个阶段(以曲线中两个明显的拐点把曲线划分为3 部分)：第一阶段可以大致看做弹性阶段，在这一阶段，聚脲材料的应力和应变近似成线性关系，满足胡克定律，其斜率可以看做聚脲材料的弹性模量；第二阶段可以看做屈服阶段，在这个阶段，应力随着应变的急剧增加变化不大，表现出明显的屈服现象；第三阶段可以看做增强(强化)阶段，应变变化不大，应力却急剧增加，表现出明显的应力强化现象。

此外，聚脲材料在不同应变率下的应力-应变特性也不尽相同，表现出明显的应变率效应。在应变相同时，随着应变率增加，应力也会增加，且在中低应变率下增加幅度较小，在高应变率下增加的幅度较大，说明聚脲材料在高应变率下的应变率效应更加显著。在高应变率时，聚脲材料应力-应变的第二阶段、第三阶段均比中低应变率的时候这两个阶段提前发生，表现出明显的应变滞后性，即在高应变率下，由于加载速度过快，应力会随着加载而迅速增大，但应变来不及变化，跟不上应力变化的速度，所以呈现出较强的应变滞后性。

一般采用弹性模量、屈服强度和切线模量等参数来表征材料的力学性能特性。对于聚脲材料来说，随着应变率的增加，聚脲材料的弹性模量、屈服强度和切线模量也在增加，所以对聚脲材料的动弹性模量、动态强度因子和动态切线模量进行研究，以充分了解聚脲材料的动态力学特性，为建立聚脲材料模型和动态数值模拟打下良好基础。

1.2 动弹性模量

从图1 可以看出，在聚脲材料力学行为的弹性阶段，不同应变率下的弹性模量也不同，在中低应变率下，弹性模量变化不大，在高应变率下，弹性模量相比准静态变化很大，随着应变率的增加，弹性模量呈现出大幅增大的趋势。

为了表征聚脲材料的动态弹性模量特性，引入弹性模量动态增大因子DIF(E)：

式中：DIF(E)为关于弹性模量的动态增大因子；Ej为某一应变率下聚脲材料在第一阶段的动弹性模量值；E0为准静态情况下聚脲材料在第一阶段的弹性模量值。

本文汇总了国内外研究者对聚脲材料进行的准静态、动态压缩试验得到的应力-应变关系，提取相应的屈服强度，计算其弹性模量，然后，计算不同应变率下弹性模量对应的DIF(E)值，并进行拟合，得到了如图2 所示的聚脲弹性体材料弹性模量增大因子随应变率变化的关系图。

从图2 可以看出，聚脲材料的DIF(E)随应变率的对数大致呈双线性关系。第一个直线应变率的范围大致为0.001 s−1～400 s−1，在这个阶段，应变率相对较低，其线性关系的斜率较小，直线比较平缓且接近水平，说明聚脲材料的DIF(E)随应变率对数的增加缓慢增加；第二个直线应变率的范围大致为400 s−1～10 000 s−1，应变率比较高，其线性关系的斜率较大，直线很陡，聚脲材料的DIF(E)随应变率对数的增加迅速增加，说明聚脲材料在高应变率下弹性模量迅速增大，表现出较强的应变率效应。

图2 聚脲材料弹性模量动态增大因子随应变率变化关系Fig. 2 The relationship between elastic modulus dynamic increase factor of polyurea and the strain rate

拟合结果可以用两个不同参数的线性关系式来表示：

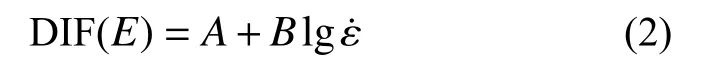
式中： ε˙为应变率值；A和B分别为拟合的双直线的截距和斜率，表征应变率效应，其值见表1。

表1 DIF(E)随ε˙对数变化关系拟合参数表Table 1 Fitting parameter table of the relationship between DIF(E) and the logarithm of ε˙

1.3 动态强度因子

从图1 可以看出，聚脲材料在不同应变率下的屈服强度也不同，随着应变率的增加，屈服强度也不断增加：在中低应变率的时候，屈服强度增加不大；但在高应变率的时候，屈服强度比准静态增大好几倍。因此，引入动态强度因子DIF(σ)来表征聚脲材料强度的应变速率效应：

式中：DIF(σ)为动态强度因子；σj为某一应变率下聚脲材料的屈服强度值(取第一阶段末第二阶段初的应力值为屈服强度)；σ0为准静态情况下聚脲材料的屈服强度值。

根据上面提取的屈服强度，计算其对应的DIF(σ)值并进行拟合，得到如图3 所示的聚脲弹性体材料动态强度因子随应变率变化的关系图。

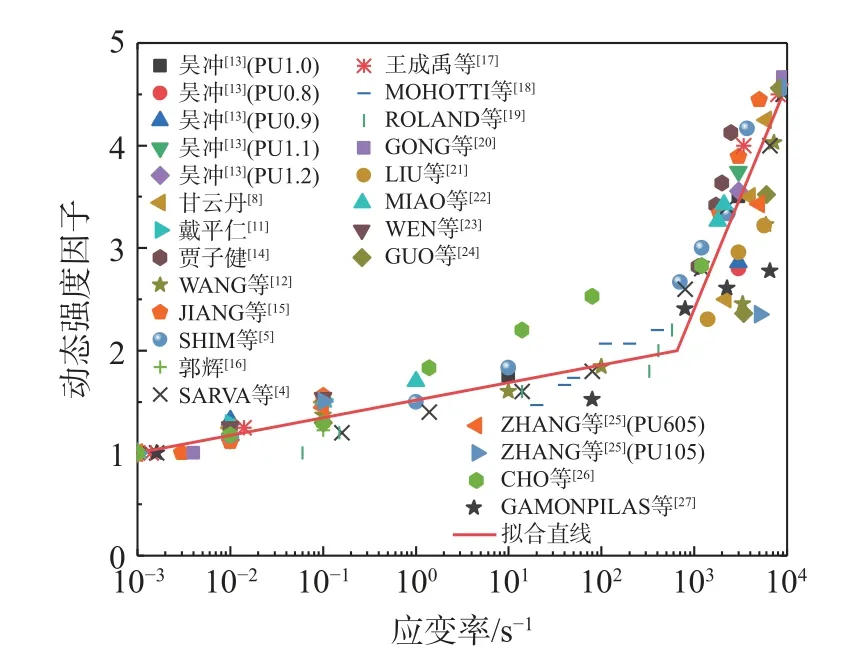
图3 聚脲材料动态强度因子随应变率变化关系Fig. 3 The relationship between the dynamic intensity factor of polyurea and the strain rate

从图3 中可以看出，聚脲材料的DIF(σ)随应变率对数的关系与DIF(E)随应变率对数的关系类似，大致呈现出双线性关系。第一个直线应变率的范围大致为0.001 s−1～630 s−1，在这个阶段，应变率相对较低，其线性关系的斜率较小，直线比较平缓，说明聚脲材料的DIF(σ)随应变率对数的增加缓慢增加；第二个直线应变率的范围大致为630 s−1～10 000 s−1，应变率比较高，其线性关系的斜率较大，直线比较陡，聚脲材料的DIF(σ)随应变率对数的增加迅速增加，说明聚脲材料在高应变率下应变率效应更加显著。

拟合结果同样可以用两个不同参数的线性关系式来表示：

式中，C和D分别为拟合的双直线的截距和斜率，表征应变率效应，其值见表2。

表2 DIF(σ)随ε˙对数变化关系拟合参数表Table 2 Fitting parameter table of the relationship between DIF (σ) and the logarithm of ε˙

对比弹性模量的DIF(E)和屈服强度的DIF(σ)的拟合结果发现：在低应变率下，拟合直线的斜率和截距相差不大；在高应变率下，弹性模量随应变率对数变化的线性关系斜率更陡，其斜率是DIF(σ)拟合斜率的5 倍左右，说明在高应变率下，线弹性阶段的应力范围值的增加明显大于材料进入屈服阶段后观察到的应力范围值的增加，也验证了高应变率下应变的滞后性。

1.4 动态切线模量

从图1 可知，聚脲材料应力-应变曲线的第二、三阶段可以看作2 段具有固定切线模量的直线，且随着应变率的增加，其相应的切线模量也随之增加，特别是在高应变率下第三阶段的切线模量增幅更是明显。因此，为表征这一特性，这里也引入动态切线模量因子DIF(ET)：

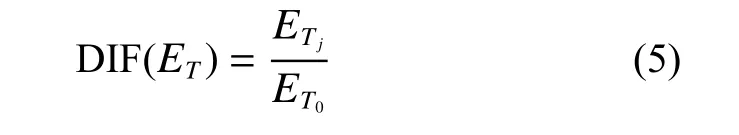
式中：ETj为某一应变率下聚脲材料应力应变曲线的切线模量；ET0为准静态情况下聚脲材料应力-应变曲线的切线模量。

对聚脲应力-应变曲线第二、三阶段进行线性拟合，得到其对应的切线模量，再计算动态切线模量因子并进行拟合，得到了如图4、图5 所示的聚脲弹性体材料的动态切线模量因子随应变率变化的关系图。由图4、图5 可知，动态切线模量因子和应变率对数的关系也呈现出较好的双线性关系。

图4 聚脲材料第二阶段动态切线模量因子随应变率变化关系Fig. 4 The relationship between the dynamic tangent modulus factor of polyurea in the second stage and the strain rate

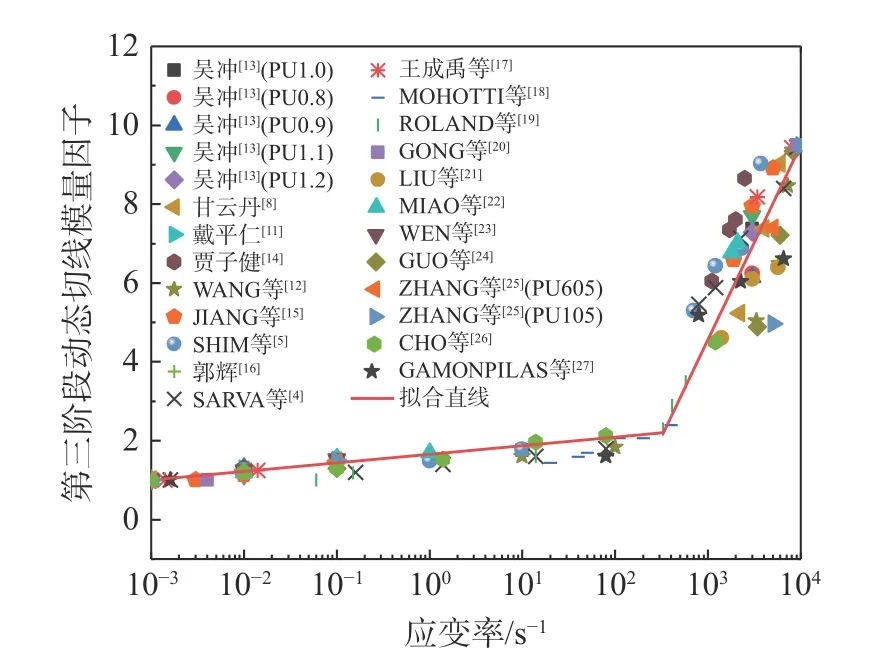
图5 聚脲材料第三阶段动态切线模量因子随应变率变化关系Fig. 5 The relationship between the dynamic tangent modulus factor of polyurea in the third stage and the strain rate

同样，拟合结果可以用两个不同参数的线性关系式来表示：

式中：Ei和Fi为表征应变率效应的参数，i=1 和2；E1、F1为第二阶段的截距和斜率；E2、F2为第三阶段的截距和斜率，其值分别见表3 和表4。

表3 DIF(ET1)随ε˙对数变化关系拟合参数表Table 3 Fitting parameter table of the relationship between DIF(ET1) and the logarithm of ε˙

表4 DIF(ET2)随ε˙对数变化关系拟合参数表Table 4 Fitting parameter table of the relationship between DIF(ET2) and the logarithm of ε˙

从拟合结果可以看出，在中低应变率下，第二阶段和第三阶段的拟合直线斜率均较小，两者相差不大，表明中低应变率下两个阶段的动态切线模量因子随应变率增加而缓慢增加，且增加幅度相近；在高应变率下，第二阶段和第三阶段的拟合直线均变陡，斜率变大，且第三阶段拟合得到的直线斜率更大，约为第二阶段的2.3 倍，表明高应变率下两个阶段的动态切线模量因子随应变率增加而快速增加，且第三阶段的比第二阶段的增幅更大。与动态强度因子的拟合结果进行比较，在中低应变率下，三者的拟合斜率相差不多；在高应变率下，第二阶段的动态切线模量因子拟合斜率与动态强度因子的相差不大，而第三阶段动态切线模量因子的拟合斜率则是动态强度因子的2.3 倍左右，说明了高应变率下聚脲材料在第三阶段的应力强化效应更加显著。

2 聚脲材料动态压缩本构模型

2.1 基本思想

根据第1 节所讨论的内容，聚脲材料的力学行为大致可以分为3 个阶段，在每个阶段其应力-应变曲线的斜率基本变化不大，因此可以将其简化为3 段固定斜率的直线，如图6 所示。此外，聚脲材料的弹性模量、屈服强度和切线模量都具有较强的应变率效应，且加载的应变率越高，其弹性模量、屈服强度和切线模量提高就越大。前文引入的弹性模量动态增大因子、动态强度因子、动态切线模量因子随应变率的对数变化拟合曲线也充分反应这一特征。因此，为便于数值分析，本文将聚脲材料动态压缩本构模型简化为在准静态三直线模型基础上考虑弹性模量动态增大因子、动态强度因子和动态切线模量因子的简化弹塑性本构模型。下面具体讨论该模型在有限元软件中的实现。

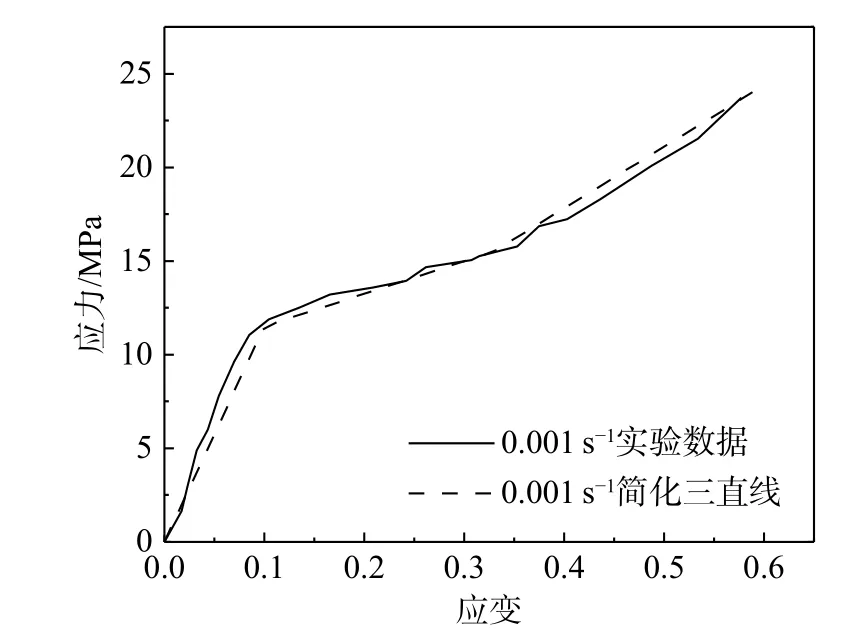
图6 三直线简化应力-应变关系图Fig. 6 Simplified stress-strain relationship diagram with three straight lines

2.2 简化弹塑性本构模型

ANSYS/LS-DYNA 显式非线性动力分析程序被广泛应用于爆炸与冲击等动力学问题，在LSDYNA 材料库中选择既满足三段式弹塑性模型又会考虑动力特性的材料模型，发现24 号关键字的材料本构模型恰巧满足这两点需求，即MAT_PIECEWISE_LINEAR_PLASTICITY 模型。

该模型是应用最广泛的弹塑性材料模型之一，通过输入准静态应力-应变关系和应变率效应参数来定义不同应变率下的应力-应变关系，该模型的屈服应力与塑性应变的关系为：

浦口区监测点种植作物大体分为粮食作物、蔬菜作物、苗木三大块，但监测点田块随各地农业结构调整不同、当地作物种植效益差别较大，农户自由选择种植作物，对监测成效有一定的影响。

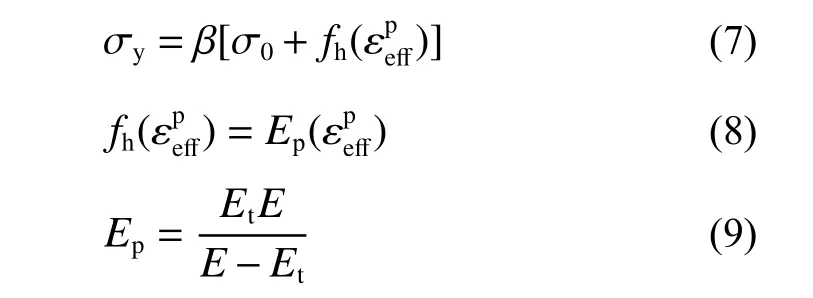
式中：σ0为初始屈服应力；为有效塑性应变；β 为应变率效应参数，E为弹性模量；Et为切线模量；fh( )、Ep( )为函数。显然，这种方法只能表示双线性形式。

为了推广至三直线模型，可以输入有效应力与有效塑性应变的表格来定义塑性阶段。所以对于聚脲材料来说，可以采用三点定义两个具有恒定切线模量的准静态塑性阶段，典型曲线如图7所示。

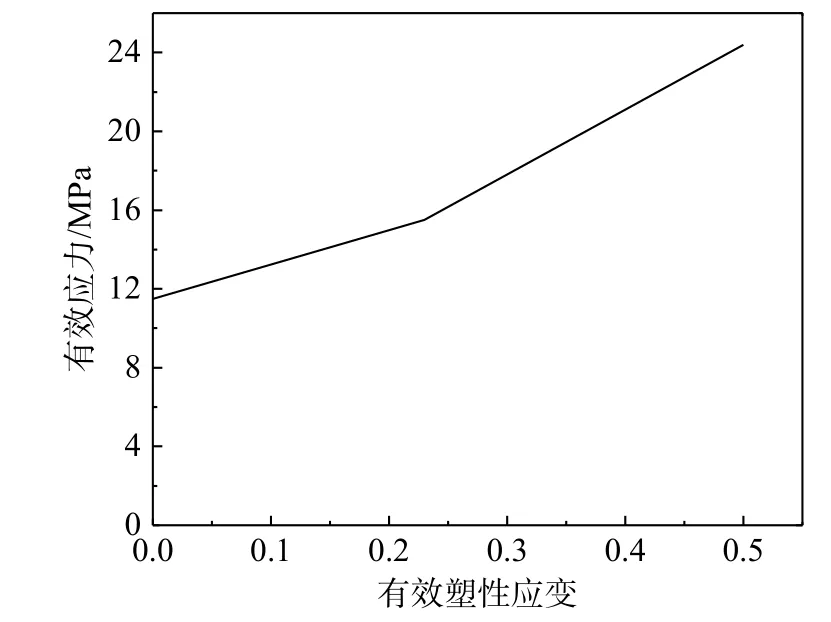
图7 三点定义的准静态有效应力-有效塑性应变曲线Fig. 7 Quasi-static effective stress-effective plastic strain curve defined by three points

图8 三点定义的修正准静态有效应力-有效塑性应变曲线Fig. 8 Modified quasi-static effective stress-effective plastic strain curve defined by three points

综上所述，本文提出的聚脲材料三直线弹塑性本构模型可以通过输入有效应力-有效塑性应变曲线和DIF(σ)、 ε˙的关系曲线以及考虑不同应变率下的动弹性模量来定义：在中低应变率下，输入有效应力-有效塑性应变曲线；在高应变率下，输入考虑动态切线模量因子修正后的有效应力-有效塑性应变曲线。该简化的弹塑性本构模型形式简单，参数也比较简单易懂，后续的数值分析结果也表明其误差很小，在工程可接受范围之内，通过该模型可以更方便地实现有关聚脲材料的数值模拟分析。

3 聚脲材料动态压缩数值模拟

数值模拟的分析方法[28]可以更加方便直观地研究材料的动态压缩力学行为，同时也可以检验聚脲材料的简化弹塑性本构模型。采用ANSYS/LS-DYNA 有限元分析软件进行数值模拟，按照WANG 等[12]的试验建立1∶1 的有限元模型来还原真实工况。对于中低应变率的压缩工况，采用简化的有限元模型，只建立聚脲试件的三维有限元模型；对于高应变率的工况，按照霍普金森杆的真实尺寸，建立入射杆、聚脲试件、透射杆三部分的有限元模型。

3.1 中低应变率

3.1.1 材料模型

根据前两节讨论的内容，聚脲材料本构模型选用为本文简化的三直线弹塑性本构模型。压缩荷载工况下的材料模型参数见表5，模型均采用国际单位制，ρ 为材料密度；E为材料的弹性模量，由于弹性模量随应变率不断变化而不是固定不变的，所以根据第1 节的拟合结果，在不同的应变率下输入不同的弹性模量值，不同应变率下的弹性模量值根据式(1)、式(2)计算可得，典型值详见表6；µ为材料的泊松比；FAIL 为材料失效时的有效塑性应变，根据图1，最大的有效应变为0.6，所以取失效有效塑性应变值为0.5；LCSR为屈服强度缩放曲线，根据第1 节拟合的动态强度因子随应变率对数变化关系，导成屈服应力缩放因子和应变率的关系，见图9；ES-EPS 用来定义准静态有效应力-有效塑性应变，采用三点定义两个具有恒定切线模量的塑性阶段，参数取值见表7。

表7 准静态有效应力ES -有效塑性应变EPSTable 7 Quasi-static effective stress ES-effective plastic strain EPS

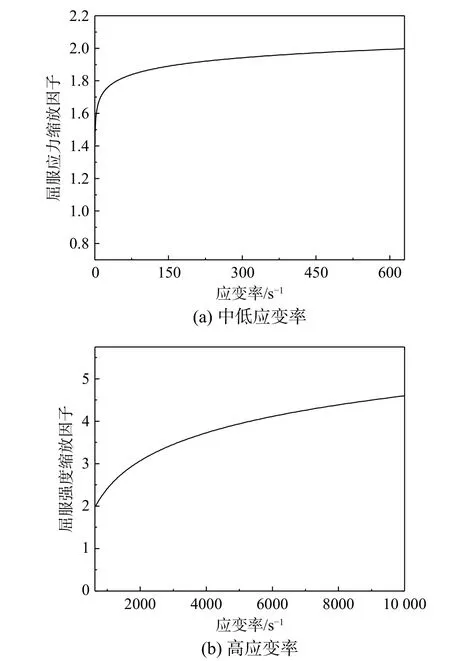
图9 屈服应力缩放因子随应变率的变化关系Fig. 9 Relationship between yield stress scaling factor and strain rate

表5 压缩荷载工况下的材料模型参数Table 5 Material model parameters under compression

表6 不同应变率压缩情况下弹性模量值Table 6 Elastic modulus of different strain rates

3.1.2 有限元模型

低应变率的压缩试件尺寸为Φ10 mm×4 mm，中应变率的压缩试件尺寸为Φ19 mm×6 mm，分别按照中、低应变率下聚脲试件的实际尺寸，采用solid164 实体单元建立聚脲试件的中、低应变率有限元模型；建模过程中网格划分方式为映射网格方式，均划分为六面体单元。由于聚脲材料在压缩荷载下的大变形特性，为了防止网格变形过大带来的负体积现象，试件网格划分较密，且径向划分比长度方向划分更密集；在试件的下部添加Z方向的约束来固定一端，上部施加沿Z方向的压缩位移荷载来进行匀速加载；沙漏控制采用全局增加弹性刚度的方式，沙漏系数采用默认值0.1。建立的中低应变率压缩有限元模型见图10。

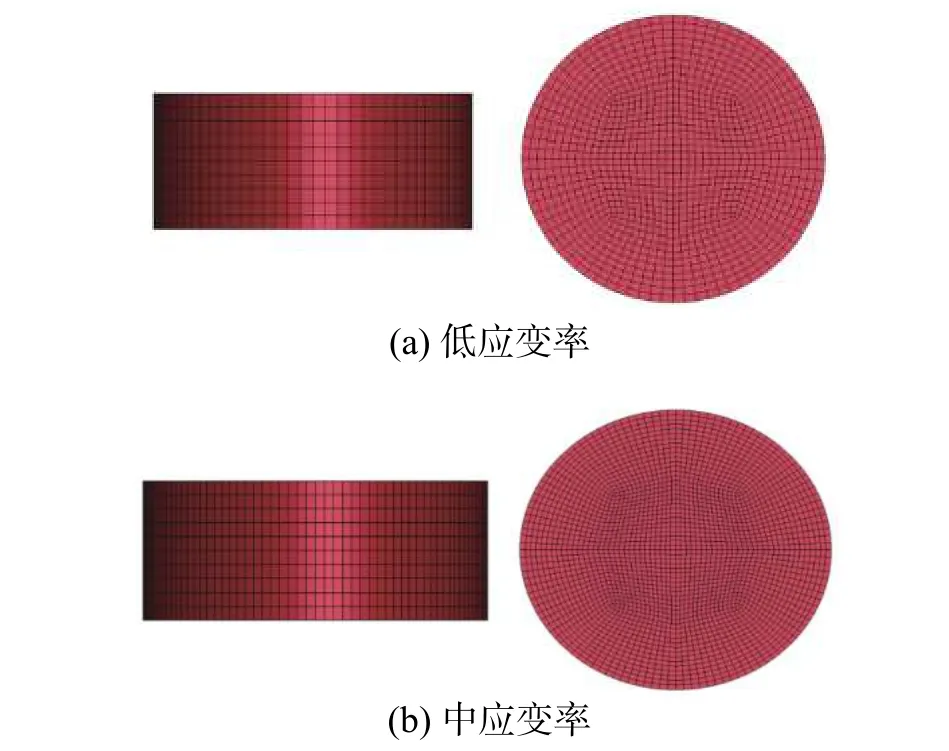
图10 中、低应变率压缩有限元模型Fig. 10 Compression finite element model of low and intermediate strain rates

3.1.3 模拟结果

对中、低应变率压缩工况下数值模拟的结果进行分析，调取试件单元的应力-应变关系，并与图1试验结果进行对比，绘制如图11 所示的应力-应变关系对比图。从对比图中可以看出，中、低应变率压缩数值模拟得到的应力-应变关系与试验应力-应变吻合较好，尤其在第二阶段即大变形阶段，屈服强度值吻合程度也很高，说明中低应变率压缩数值模拟采用的方法是理想的，采用的简化弹塑性本构模型在中、低应变率下是可靠的。

图11 中、低应变率压缩试验和模拟应力-应变关系对比图Fig. 11 Comparison chart of compression test and simulated stress-strain relationship under low and intermediate strain rates

3.2 高应变率

3.2.1 材料模型

聚脲材料有关参数取值在中、低应变率压缩部分已经给出，对高应变率下的屈服应力缩放因子随应变率的变化关系见图9，动弹性模量取值按式(1)、式(2)计算，参见表6，聚脲采用修正后的准静态有效应力-有效塑性应变来定义2 个具有恒定切线模量的塑性阶段，参数取值见表8。对于入射杆和透射杆材料，均采用线弹性本构模型，其参数见表9。

表8 修正准静态有效应力ES-有效塑性应变EPSTable 8 Modified quasi-static effective stress ES-effective plastic strain EPS

表9 入射杆、透射杆材料模型Table 9 Material model of incident and transmission bar

3.2.2 有限元模型

对聚脲材料来说，薄试件有利于尽早实现应力平衡、减弱试件中应力波的衰减，保证试件中应力的均匀，通常试件长径比取值在0.25～0.5 即可满足要求，此外试件横截面积在整个实验过程中不得超过压杆的横截面积。因此，参照文献[12]，入射杆、试件和透射杆的尺寸分别取Φ19 mm×1200 mm、Φ10 mm×4 mm 和Φ19 mm×1200 mm。采用Solid164 实体单元、映射网格划分的方式建立三部分的1/4 有限元模型，在试件处加密网格的划分，入射杆、透射杆的网格可以相对稀疏；由于只建立了1/4 模型，所以在入射杆、试件和透射杆的对称面上施加对称约束；入射杆和试件、试件和透射杆的接触均采用自动面面接触，取不同的罚因子值来进行数值模拟，发现当罚因子值为0.5 的时候，模拟结果最为理想，所以罚因子值均设置为0.5，此外为保证一维应力波假定，实验时在试件和杆件的接触端面均涂抹润滑剂以减小端面摩擦，摩擦效应很小可忽略不计，因此在数值模拟中也不计入摩擦；时间步长因子从默认的0.9 减小为0.6，以防止试件发生负体积现象导致的计算终止；沙漏控制依旧采用全局增加弹性刚度的方式，沙漏系数采用默认值0.1。聚脲材料的高应变率有限元模型见图12。

图12 SHPB 有限元模型Fig. 12 SHPB finite element model

为了减小波形整形器等带来的对输入波(入射波)的误差，根据文献[12]中给出的应变率为5901.35 s−1时通过应变片测得的入射杆上的力随时间的变化关系，可以得到入射杆上的应力随时间的变化关系，将得到的入射波数据作为荷载加在入射杆端面，来代替子弹对入射杆的撞击作用。

3.2.3 模拟结果

导出SHPB 有限元模型结果中入射波、反射波和透射波的的波形图，并与试验得到的波形图进行对比，对比结果如图13 所示，可以看出两者几乎吻合，所以采用入射波加载的方法和传统的模拟子弹速度进行加载的方法相比，可以保证模拟波形与试验波形差距不大，有效减小霍普金森杆数值模拟的误差。

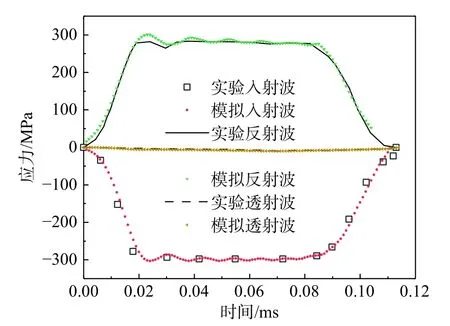
图13 试验波形与模拟波形对比图Fig. 13 Comparison chart of test wave and simulated wave

对高应变率压缩数值模拟的结果进行分析，提取试件应力-应变值，得到高应变率压缩下数值模拟的应力-应变关系，并与图1 试验结果进行对比，绘制如图14 所示的应力-应变关系对比图。若聚脲采用未修正的有效应力-有效塑形应变曲线(图7)，其数值模拟结果也绘制在图14 中。

图14 高应变率压缩试验和模拟应力-应变关系对比图Fig. 14 Comparison chart of compression test and simulated stress-strain relationship under high strain rate

从图14 可以看出，无论是采用修正和未修正的有效应力-有效塑性应变曲线模型，高应变率下压缩数值模拟得到的应力-应变曲线在第一、二阶段均与试验数据吻合较好，但在第三阶段采用未修正曲线的模拟结果相对试验结果明显偏小，这是因为在高应变率下，聚脲材料的第三阶段的应力强化效应要比第二阶段的大，且会提前发生，此时再采用中低应变率下的应力-应变参数，忽略高应变率下第二、三阶段动态切线模量因子差异来模拟高应变率下的应力-应变时就会出现第三阶段偏小的情况。而采用考虑第三阶段动态切线模量因子修正曲线的模拟结果则与试验结果基本一致，说明高应变率下聚脲材料的压缩数值模拟必须考虑第三阶段应力快速增长的强化效应，也表明了本文建立的简化弹塑性本构模型是准确的。

总而言之，在低、中、高三种不同应变率下有限元数值模拟的结果是理想的，说明采用本文提出的聚脲材料考虑动弹性模量、动态强度因子和动态切线模量的三直线简化弹塑性本构模型构建方法和相关参数取值是可靠的。

4 结论

本文通过分析汇总国内外学者对聚脲材料进行不同应变率的压缩实验结果，研究其动态压缩力学特性，构建聚脲材料的动态本构模型，并进行数值模拟分析，得出以下结论：

(1) 聚脲材料弹性模量动态增大因子、动态强度因子、动态切线模量因子和应变率的对数均呈双线性关系。在中、低应变率下，三者的线性关系斜率都比较平缓；在高应变率下，三者的线性关系斜率都比较陡，且弹性模量动态增大因子的斜率比动态强度因子的更大，直线更陡，说明聚脲材料在高应变率下，应变率效应更加明显且存在应变滞后现象，第二阶段的动态切线模量因子斜率与动态强度因子的基本一致，但第三阶段的动态切线模量因子斜率是动态强度因子的2.3 倍左右，说明高应变率下聚脲材料的后期应力强化效应更加显著。

(2) 构建聚脲材料考虑应变速率效应的简化三直线弹塑性本构模型，并提出在ANSYS/LS-DYNA有限元软件中的实现方法。通过在塑性变形域中使用2 个具有恒定切线模量的区间，来简化聚脲材料力学行为的屈服强化阶段，在中、低应变率下，输入有效应力-有效塑性应变曲线；在高应变率下，输入考虑动态切线模量因子修正后的有效应力-有效塑性应变曲线。通过定义屈服强度缩放因子、弹性模量动态增大因子随应变率变化的关系，来考虑强度和弹性模量的应变速率效应。

(3) 基于LS-DYNA 有限元分析软件，建立聚脲在中、低、高应变率下的动态压缩有限元模型。数值模拟得到的应力-应变关系与试验得到的结果吻合较好，说明本文构建的考虑应变率效应的三直线简化弹塑性聚脲材料本构模型的方法是可靠、有效的，这也为采用数值模拟的方法进一步研究聚脲防爆材料的动力学响应提供了坚实的基础。