波纹腹板增强泡沫夹芯复合材料结构准静态压缩吸能特性

沈春燕，方 海，祝 露，韩 娟，郁嘉诚

(南京工业大学土木工程学院，江苏，南京 211816)

近年来，由于交通运输量的不断增加，时常发生车辆、船舶撞击桥梁的交通事故，不仅造成了严重的生命财产损失，而且危及了桥梁结构的安全性。所以无论是车桥还是船桥撞击，都是不容忽视的科学问题，受到了工程界的广泛关注[1−2]。桥梁墩身采用防撞设施是目前最广泛的措施之一，主要通过吸能来降低车船的撞击力。然而现阶段的防撞设施主要采用混凝土、钢等材料，虽成本较低，但存在耐腐蚀性能差、维修成本高以及刚度大等问题。近年来，纤维增强复合材料(Fiber reinforced polymer，简称FRP)学术研究热度与日俱增，其具有较好的吸能特性、耐腐蚀性和可设计性[3−6]，逐步被应用于航天航空、汽车、桥梁等防撞吸能领域[7]。

传统的复合材料夹芯结构主要由上下面板和芯材构成，面板主要提供强度和刚度，轻质芯材能有效降低整体结构的重量。但承载时，面板与芯材之间易发生层间剥离，大大降低了夹芯结构的抗剪、抗压强度与吸能特性。针对此难题，2008 年，KELLER 等[8]采用纵向腹板增强复合材料夹芯结构作为屋面板，结果发现：设置纵向腹板可以极大改善夹芯结构的整体性，较好解决了夹芯结构存在的面板与芯材剥离情况，提高了结构的承载力和刚度。魏凯耀等[9]研究了整体缝合夹芯结构复合材料的受压承载力和破坏模式，结果表明：缝合纱线数量的增加能显著提高夹芯结构的压缩强度和压缩模量。SHI 等[10]发明了复合材料泡沫或轻木型夹芯材料，有效提高了夹芯结构抗剥离性能，且构件具有一定的延性。

在复合材料夹芯结构受力性能研究领域，韩宾等[11−12]首次提出聚氨酯泡沫填充波纹夹芯结构，通过理论公式推导，发现其结构面内破坏行为，并将理论结果与有限元数值模拟结果进行对比，结果较吻合。REJAB 等[13]通过压缩试验对铝合金、玻璃纤维增强塑料、碳纤维增强塑料三种材料的波纹夹芯板力学性能开展了相关研究，并采用有限元软件对试验结果进行了数值模拟，结果表明：复合材料夹芯结构的力学性能优于金属材料夹芯结构。SHABAN 等[14]通过理论计算，得到了波纹夹芯板结构的等效几何参数，研究表明：波纹夹芯板在厚度方向上的弹性模量随着芯材厚度的增大而减小。洪俊青等[15]基于高阶剪切变形理论有限元方法对泡沫芯材-GFRP 面板增强层进行分析，结果表明：利用等效截面法计算得出的泡沫夹芯板正应力偏小，有限元结果与试验结果更加符合。石昌等[16]研究了梯形格构腹板增强泡沫夹芯板在平面压缩载荷下的失效模式和力学性能，结果表明：夹芯板主要发生格构腹板断裂与屈曲破坏；夹芯板的压缩性能随着格构腹板角度与腹板厚度的增加而提高。罗熠民等[17]研究了纤维增强复材夹芯板的弯曲性能和破坏模式，结果表明：增加横向格构可以减少板材的损坏，增加纵向格构可以有效提高夹芯板的抗弯承载力。此外，国内外学者对于纤维增强复合材料的能量吸收行为也进行了相关研究。YAZICI 等[18]提出将泡沫作为芯材应用于波纹夹芯结构，通过一系列试验，研究填充泡沫对夹芯结构吸能特性以及减振性能的影响，结果表明：泡沫的填充可有效提高波纹夹芯结构的减震性能和吸能特性，提升近一倍。杨鹏飞[19]通过数值模拟与试验研究了波纹夹芯板的吸能特性，结果表明：增加面板厚度对提高结构吸能的影响不大，但能有效增加结构刚度。潘丹等[20]对复合层状结构进行了横向静态压缩试验研究，该结构主要由发泡聚乙烯(Expandable polystyrene，简称EPE)、瓦楞纸板和蜂窝纸板组成，结果表明：随着试样厚度的增加，复合层状结构的弹性模量、总吸能均高于EPE。由上述研究可知，目前关于腹板增强复合材料夹芯结构的研究多集中于构件的受弯、受剪性能；同时，现有的缓冲吸能结构多为空心管或者泡沫填充管，此类吸能构件峰值荷载和屈服平台力较小，不利于抵抗大能量的冲击荷载。本文提出了一种新型的波纹腹板增强泡沫夹芯复合材料吸能结构(见图1)，其中，波形格构腹板的布置形式及其波长、壁厚等均可根据冲击能量实现可控设计。

图1 试件内部结构Fig. 1 The internal structure of specimens

本文主要研究不同波形格构腹板层数、壁厚以及波长的夹芯结构在准静态压缩试验下的破坏模式和吸能特性。并运用ANSYS/LS-DYNA 对试件准静态压缩试验进行数值模拟与参数分析，为该新型复合材料吸能结构应用于实际工程提供参考。

1 制备和试验

1.1 波纹腹板泡沫夹芯试件设计与制备

本文将采用双层正交波纹腹板和三层正交波纹腹板两组试件进行试验研究。试件采用真空导入工艺制备，试件原材料包括聚氨酯泡沫(密度为40 kg/m3)、(0°/90°)双轴向玻璃纤维布(密度为800 g/m2)、不饱和聚酯树脂与1.2%过氧化甲乙酮固化剂。制备过程主要分为3 个部分：1)利用电阻丝切割出波纹型的聚氨酯泡沫芯材，如图2(a)所示；2)在切割好的泡沫间隙铺设(0°/90°)玻璃纤维布，并将其整体铺设于(0°/90°)玻璃纤维布的模具中，如图2(b)所示；3)在其周围铺设导流管、脱模布、盖板等，利用导流管导入添加固化剂的树脂，待树脂固化后拆模并切割成型，如图2(c)所示。

图2 试件制备过程Fig. 2 The manufacture of specimens

1.2 材性试验

依据规范《玻璃纤维增强塑料拉伸性能试验方法》(GB/T 1477−2005)[21]和《硬质泡沫塑料压缩性能的测定》(GB/T 8813−2008)[22]分别对GFRP 片材与聚氨酯泡沫进行了相关材性试验。每组试验构件各加工5 个。采用200 kN 的万能试验机，使用东华静态应变仪采集试件应变数据。其中，GFRP片材拉伸试件尺寸为250 mm×25 mm×2.5 mm，聚氨酯泡沫芯材压缩试件尺寸为50 mm×50 mm×50 mm，拉伸与压缩试验加载速度均为2 mm/min，试验结果见表1 和表2，其中，聚氨酯泡沫芯材压缩应力-应变曲线见图3。

图3 聚氨酯泡沫应力-应变曲线Fig. 3 Stress-strain curve of polyurethane foam

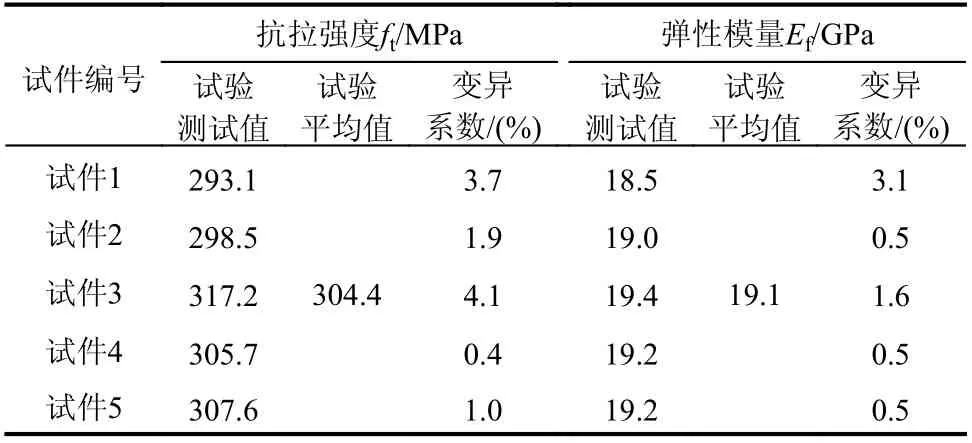
表1 GFRP 片材拉伸试验结果Table 1 Results of tensile test on GFRP sheet

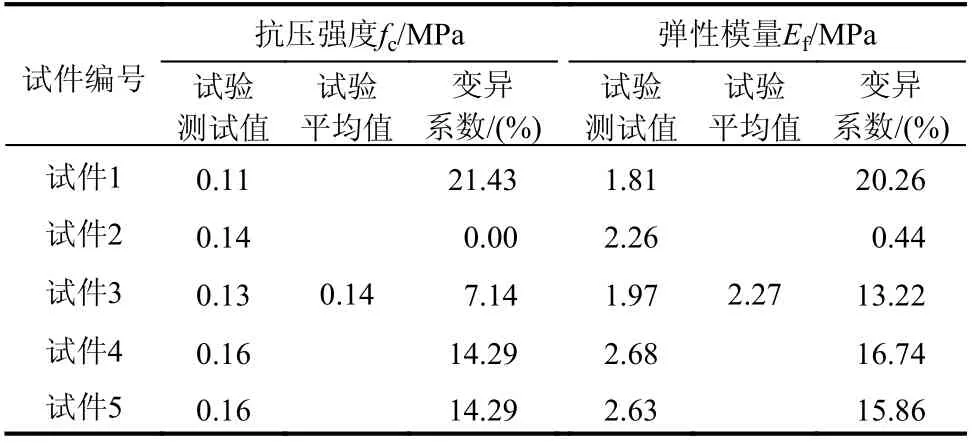
表2 聚氨酯泡沫芯材压缩试验结果Table 2 Results of compression test on polyurethane foam

1.3 复合材料结构准静态压缩吸能试验

依据《夹层结构或芯子平压性能试验方法》(GB/T 1453−2005)[23]中的规定对波纹腹板增强泡沫夹芯复合材料吸能结构进行准静态压缩试验，仪器采用量程为600 kN 的万能试验机，以2 mm/min的压缩速度连续加载。本文共设计8 个试件，试验装置见图4，试件尺寸见表3。

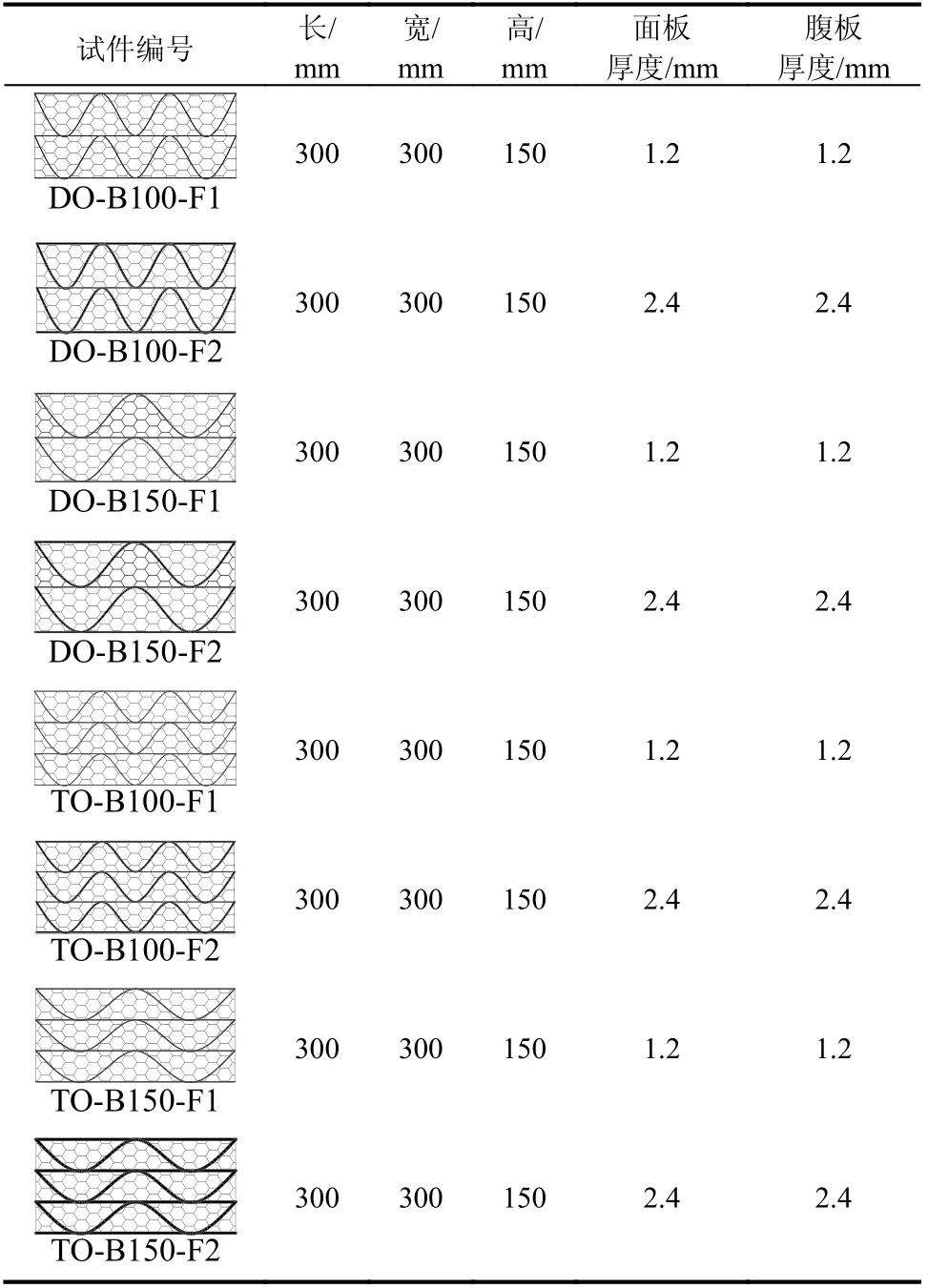
表3 试件的尺寸参数Table 3 Dimension parameters of specimens

图4 试件加载Fig. 4 The loading process of specimens

1.3.1 破坏形态

双层正交波纹腹板结构主要存在底层泡沫撕裂与格构腹板层间剥离两种破坏模式，且一般底层泡沫撕裂先于格构腹板层间剥离发生。在初始压缩阶段，构件的承载力呈非线性上升。当压缩量分别为8.4 mm 和9.4 mm 时，DO-B150-F1 和DOB100-F1 的底层泡沫开始发生撕裂，并伴有清脆的响声，如图5(a)所示。随着压缩量的增加，当试件压缩量分别达到15.1 mm 和18.1 mm 时，DOB150-F1 和DO-B100-F 的底层泡沫与格构之间发生层间剥离现象，随着位移量的增大，剥离现象变得严重并出现空腔，如图5(b)所示。泡沫撕裂主要由于构件左右两侧未设置纤维布包裹，受压时泡沫易受挤压而向外挤出，最终发生纵向撕裂破坏。格构腹板层间剥离破坏现象产生的原因是格构腹板与泡沫之间的粘结强度小，导致泡沫受到挤压后与格构腹板发生剥离。随着压缩量的持续增加，双层正交波纹腹板结构底层泡沫逐渐被压溃，层间剥离处裂缝继续扩大；当压缩量分别为53.1 mm 和70.0 mm 时，DO-B150-F1 和DO-B100-F2 的泡沫被压实，水平格构腹板开始被拉断，承载力下降，如图5(c)所示，最终试件被压实，承载力持续上升。DO-B100-F2 的承载力优于DOB100-F1，但DO-B100-F2 会因受压而发生脆性断裂，易导致其承载力瞬间下降。

三层正交波纹腹板结构主要存在格构腹板层间剥离和水平格构腹板弯曲两种破坏模式，且一般水平格构腹板弯曲先于格构腹板层间剥离发生，原因在于正交波纹腹板顶点并不交汇于一点。在初始压缩阶段，构件的承载力近似呈线性增长，直至达到上升阶段极限承载力。当压缩量分别为23.5 mm 和14.5 mm 时，TO-B150-F1 和TO-B100-F1 的水平格构腹板因受挤压而发生弯曲现象，且中间层左侧泡沫因挤压而破坏，如图5(d)所示。当压缩量分别为37.9 mm 和20.8 mm 时，TO-B150-F2 和TO-B100-F2 的中间层泡沫向外挤出，右侧泡沫与斜格构发生层间剥离破坏，且泡沫在纵向开始出现裂缝，如图5(e)所示。对比三层正交波纹腹板结构和双层正交波纹腹板结构，随着泡沫层数的增加，泡沫不易向外撕裂。当压缩量分别增加至78.5 mm 和84.5 mm 时，TO-B150-F1 和TOB100-F2 的底层泡沫被压实，中间层泡沫与格构腹板的层间剥离现象更加明显，如图5(f)所示，最终试件被压实，承载力持续上升。对比波长相同、格构腹板壁厚不同的试件，TO-B100-F2 的格构腹板因受压而发生断裂现象，导致其承载力瞬间下降，而腹板壁厚较小的试件，其承载力一直处于稳步上升阶段，未出现格构断裂现象。

图5 试件破坏模式Fig. 5 The failure modes of specimens

1.3.2 荷载-位移曲线

图6 和图7 分别表示双层正交波纹腹板结构和三层正交波纹腹板结构的荷载-位移曲线。双层正交波纹腹板结构的荷载-位移曲线可以分为非线性上升、瞬间下降(DO-B100-F2、DO-B150-F2)、平台稳定与波动上升四个阶段。由图6 可知，DOB100-F1 的承载力呈先快速上升，后缓慢上升的非线性模式，当承载力上升至37.55 kN 时，由于泡沫与斜格构之间发生层间剥离，其承载力不再上升且处于较长的平台稳定状态，当泡沫被压实，其承载力将继续上升。当增加格构腹板壁厚时，DO-B100-F2 的承载力在上升阶段达到了53.13 kN，较DO-B100-F1 提高了41.5%，而后中间水平格构因受挤压发生断裂，导致其面板与加载头之间出现小段空隙，承载力连续下降两次，下降幅度达到44.8%，最终试件开始被逐渐压实且后期部分格构被压断，出现承载力波动上升的现象。对于较长波长的DO-B150-F1，其承载力的上升趋势与DOB100-F1 类似，先快速上升后缓慢上升，直至承载力上升至26.13 kN，较DO-B100-F1 降低了30.4%。后期承载力一直处于稳定状态，未出现格构断裂现象，仅出现局部的层间剥离与泡沫断裂。DOB150-F2 由于腹板壁厚的增加，其初始上升阶段的最大承载力提升至36.93 kN，较DO-B150-F1 提高了41.3%。当压缩量达到21.8 mm 时，承载力大幅下降至14.46 kN，主要由于底层泡沫发生撕裂破坏，且中间水平格构与顶层斜格构交界处突然发生水平格构断裂现象，与泡沫一起出现破坏，如图6 所示，下降幅度高达60.8%。

图6 双层正交波纹腹板结构荷载-位移曲线Fig. 6 Load-displacement curves of specimens with doublelayer orthogonal corrugated lattice web

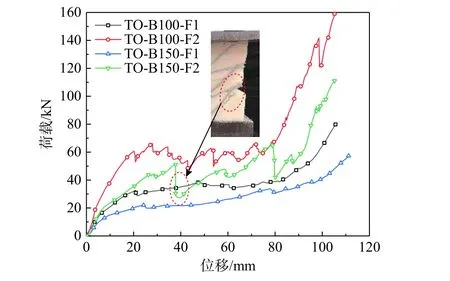
图7 三层正交波纹腹板结构荷载-位移曲线Fig. 7 Load-displacement curves of specimens with threelayer orthogonal corrugated lattice web

图7 描述了三层正交波纹腹板结构的荷载与位移关系。其荷载-位移曲线同样可以分为非线性上升、瞬间下降(TO-B150-F2)、平台稳定与波动上升四个阶段。TO-B100-F1 的承载力呈先快速上升后缓慢上升的非线性模式。当试件承载力上升至32.55 kN 时，底层泡沫开始出现裂缝且发展迅速，在短时间内完全断裂，导致承载力不再上升，开始较长的平台稳定状态。随着泡沫被压实，试件承载力持续上升。增加腹板壁厚后，TO-B100-F2 在上升阶段的最大承载力达到了54.26 kN，较TO-B100-F1 提高了66.7%。后期由于中间层左侧泡沫向外不断挤出，底层右侧泡沫与斜格构之间开始发生层间剥离并出现裂缝，进而导致承载力下降，当试件被压实，其承载力又出现波动上升的现象。TO-B150-F1 的承载力上升趋势同TOB100-F1，当承载力上升到21.86 kN 后，其承载力一直处于稳定状态，直到试件被压实才开始不断上升。TO-B150-F2 由于腹板壁厚的增加，其上升阶段的最大承载力达到51.03 kN，较TO-B150-F1提高了133.4%。当压缩量达到37.9 mm 时，试件中间层水平格构与底层右侧斜格构的连接处发生剪切撕裂破坏，导致承载力瞬间下降至26.89 kN，如图7 所示，下降幅度高达47.3%。经过此次大幅下降后，试件进入了短暂的平台稳定阶段，当试件被压实后，其承载力不断上升。

由此可见，随着腹板壁厚的增加和波长的减小，承载力会有明显的上升，但是腹板壁厚越大，发生承载力瞬间下降的可能性越大，破坏模式也易改变。当后期承载力进入平台阶段时，随着压缩量的增大，试件逐渐被压实，其承载力也持续上升。

1.3.3 能量吸收值Ea

能量吸收值Ea是指试件从开始压缩至压缩行程为试件高度70%过程中所吸收的能量。能量吸收值即荷载-位移曲线与横坐标轴(位移)所围成的面积，是评价试件吸能特性的一个主要指标，计算式如下：

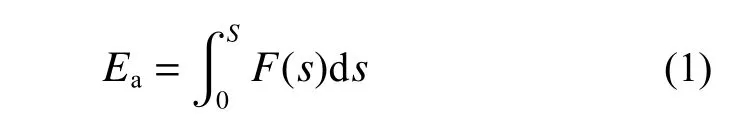
式中：S为试件压缩位移数值；F(s)为压缩位移S时对应的荷载；Ea为压缩量为S时试件的能量吸收值。

各试件随着压缩行程的增加，各阶段的能量吸收值如表4 所示。

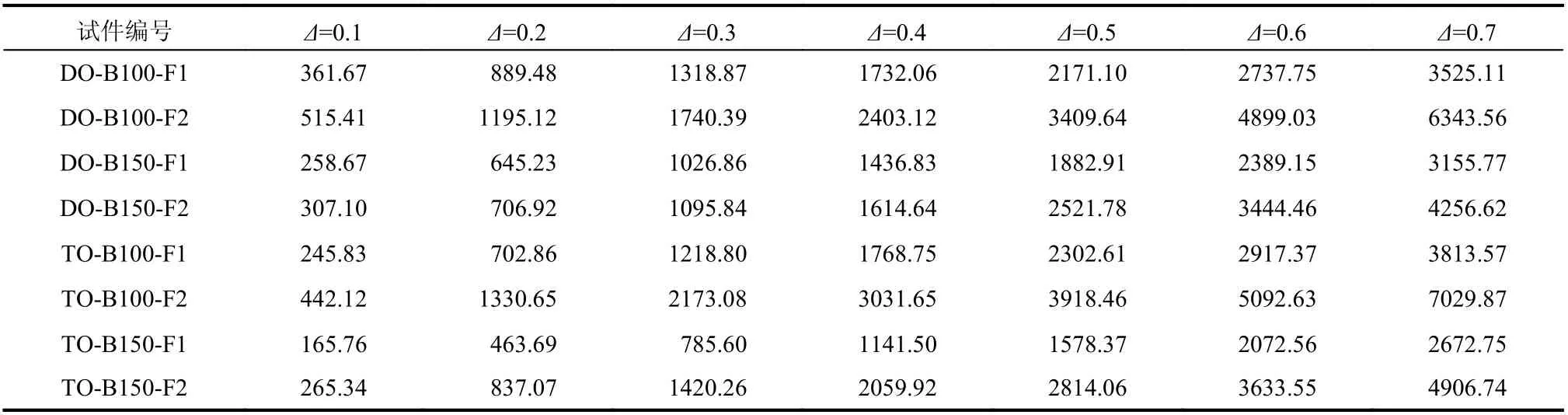
表4 试件能量吸收值Ea/JTable 4 Energy absorption of tested specimens Ea

图8 和图9 给出了双层正交波纹腹板结构和三层正交波纹腹板结构的能量吸收过程。在试件加载初期，波长越短，能量吸收越多，且一直保持到试件压缩完毕。在压缩比例达到0.4 前，DOB150-F1 和DO-B150-F2 的能量吸收值都比较接近，直至右侧水平格构与顶层斜格构交界处发生水平格构断裂，泡沫破坏，吸能效果降低。由图8和图9 可知，相同波长的试件，腹板壁厚越大，能量吸收值越大，且腹板壁厚相同的试件，能量吸收曲线的趋势也相似。最后试件被压实且吸能值呈快速上升状态。其中，DO-B150-F1 能量吸收值最小，共吸能3155.77 J。与之相比，DO-B100-F1、DO-B100-F2、DO-B150-F2 的能量吸收值分别提升了11.7%、101.2%和34.8%。由此可见，波长越短且腹板壁厚越大的试件能量吸收值越高。在加载初期，TO-B100-F2 的能量吸收值与其余三个试件相差较大。最后三层正交波纹腹板结构逐渐被压实，所有试件的能量吸收值都呈快速上升状态。结果显示，TO-B150-F1 的能量吸收值最小，共吸能2672.75 J。TO-B100-F1、TO-B100-F2、TO-B150-F2 能量吸收值较DO-B100-F1、DO-B100-F2、DOB150-F2，分别提升了42.6%、163.0%和83.6%。

图8 双层正交波纹腹板结构能量吸收Fig. 8 The energy absorption of specimens with double-layer orthogonal corrugated lattice web

图9 三层正交波纹腹板试件能量吸收Fig. 9 The energy absorption of specimens with three-layer orthogonal corrugated lattice web

1.3.4 比吸能Es

比吸能Es是单位质量试件所吸收的能量，即压缩行程S之内所吸收的总能量Ea与试件质量m之比，是评价试件吸能特性的另一个主要指标，计算式如下：

式中：Ea为试件能量吸收值；m为试件的质量。

表5 给出了各试件的比吸能。对于同一种截面形式的试件，增大格构腹板壁厚对试件比吸能会产生较大影响。大部分格构腹板壁厚小的试件比吸能较低，主要因为增大腹板壁厚的同时树脂灌入量也大幅增加，使得试件的质量增长较大。在试验过程中，腹板壁厚大的试件往往会发生格构腹板断裂的情况，最终导致承载力大幅下降，影响其吸能效果。对于同一种截面形式且格构腹板壁厚相同的试件，波长的长短对试件比吸能影响较大，一般波长越短，试件的比吸能越高。主要因为波长越短，试件承受挤压的单元体越多，吸收能量的单元体也越多，导致试件的比吸能升高，但其升高程度会因试件的结构形式而异，但一般都在10%以上。由此可见，改变腹板壁厚对试件的比吸能影响较小，而减小波长对试件的比吸能影响较大。对于同一腹板壁厚的不同截面形式的试件，TO-B100-F2 的比吸能最大，达到1774.42 J/kg。

表5 试件比吸能Table 5 Specific energy absorption of tested specimens

1.3.5 平均压溃力Fm

平均压溃力Fm是指试件在整个准静态压缩过程中的平均承载力，即压缩行程S之内所吸收的总能量Ea与压缩行程S之比，是量化试件压溃过程的重要参数之一，其表达式如下：

式中：Ea为试件能量吸收值；S为试件的总压缩量。

表6 计算了各试件的平均压溃力，对于同一种截面形式的试件，增大格构腹板壁厚能较大提高试件的平均压溃力，普遍提高30%以上。原因在于格构腹板作为试件抗压的主要部分，腹板壁厚越大，其格构腹板的抗压强度也越高。同一种截面形式且格构腹板壁厚相同的试件，其波长越短，平均压溃力越高。此外，在同一腹板壁厚不同截面形式的试件中，TO-B100-F2 的平均压溃力最大，约66.95 kN。

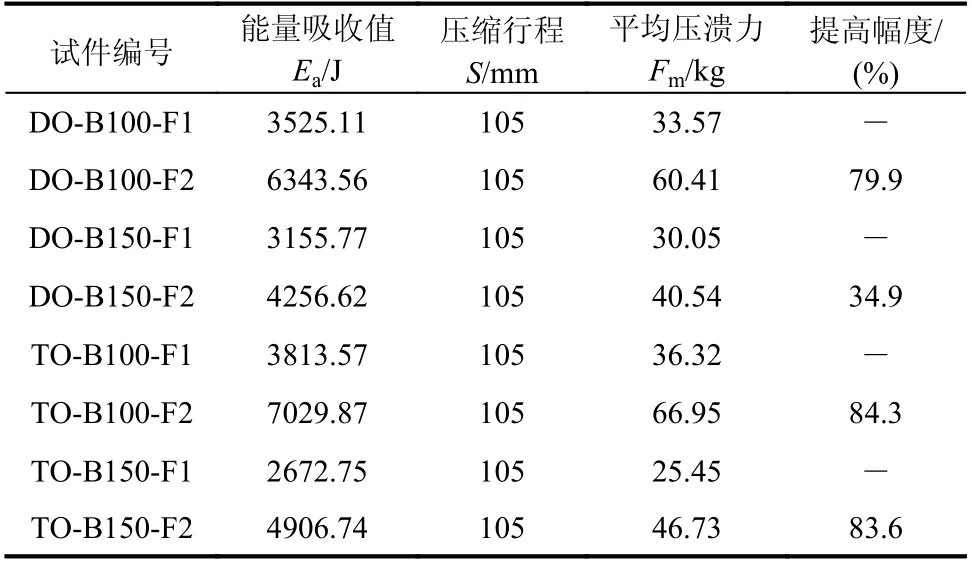
表6 试件平均压溃力Table 6 Mean crushing load of tested specimens

2 有限元数值分析模拟

2.1 有限元建模

采用ANSYS/LS-DYNA 非线性动力学有限元软件对波纹腹板增强泡沫夹芯复合材料结构的试验结果进行验证分析。其中，GFRP 采用*MAT_ENHANCED_COMPOSITE_DAMAGE 模型(第54号模型)；聚氨酯泡沫采用*MAT_Crushable_Foam模型(第63 号可压碎泡沫模型)，其中，泡沫破坏准则如式(4)所示；加载板和垫板采用*MAT_Rigid模型(第20 号刚体材料模型)。各个材料参数见表7，其中，GFRP 的X和Y方向近似采用相同的弹性模量，便于计算。

表7 材料参数Table 7 The parameters of materials

式中：ε1为主应变；εmax为最大主应变。

利用ANSYS/LS-DYNA 有限元软件中的GUI界面对试件进行1∶1 等比例建模，试件的几何模型与网格划分见图10。建模完成后将波纹腹板、面板、泡沫三者合并节点。在约束方面，下部垫板的下表面设置成全约束，约束其所有平动和转动方向。在准静态压缩试验的加载过程中，加载板采用函数加载(Specify Loads)方式，其加载速度为2 mm/min。在接触方式上，采用面面接触，其动摩擦系数和静摩擦系数均取为0.2，上下垫板与试件之间采用Tie 接触。在所有步骤完成后输出k文件进行求解，求解结果利用处理软件LSprepost 进行处理，从中提取破坏模式、荷载-位移曲线等结果。

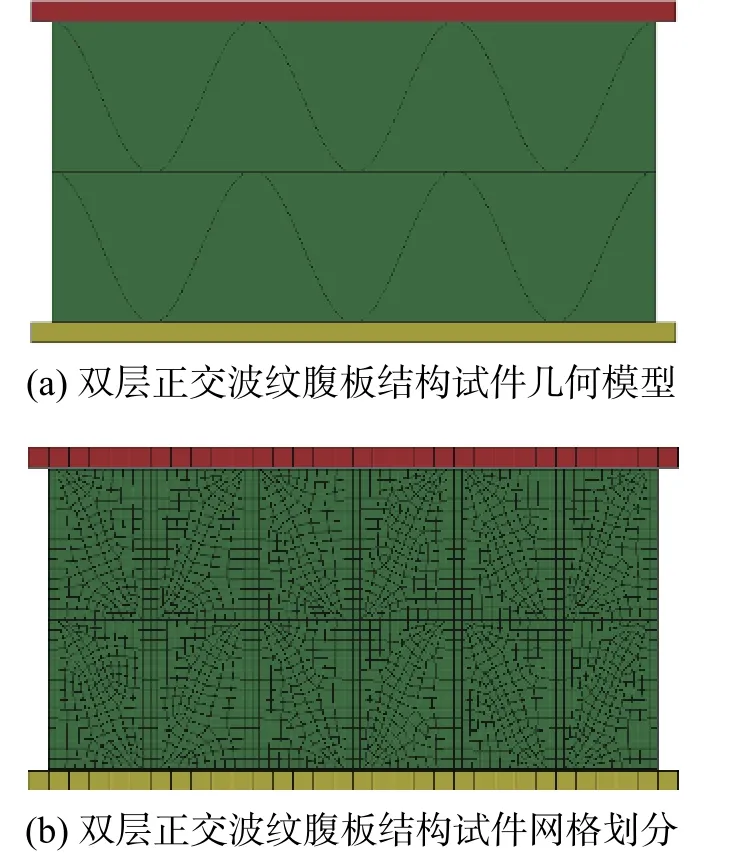
图10 几何模型及网格划分Fig. 10 Geometric model and mesh

2.2 有限元结果分析

双层正交波纹腹板结构和三层正交波纹腹板结构的有限元数值模拟所得的变形图与试验压缩变形图吻合。双层正交波纹腹板结构主要发生中间层水平格构腹板弯曲破坏，且两侧泡沫向内挤压，与试验结果相符，见图11。在数值模拟结果中，三层正交波纹腹板结构主要发生中间层水平格构受挤压弯曲破坏以及泡沫与斜格构层间剥离破坏，与试验结果相符，见图12。

图11 双层正交波纹腹板结构变形与应力云图Fig. 11 Strain and stress of specimens with double-layer orthogonal corrugated lattice web

图12 三层正交波纹腹板结构变形与应力云图Fig. 12 Strain and stress of specimens with three-layer orthogonal corrugated lattice web

图13 描述了波纹格构腹板试件的有限元模拟曲线与试验的荷载-位移曲线。在上升阶段，曲线吻合较好；后续的平台和压实阶段，由于受压作用，有限元模拟采用的泡沫模型在最大主应变达到0.1 时，单元被破坏且删除，使得整体刚度削减，导致承载力呈波动式下降，而试验中泡沫会因压实而出现承载力上升现象，这是由材料本构模型决定的。当承载力再次上升时，其模拟值的荷载-位移曲线未出现平台。其中，在有限元模拟中，试件的上升段位移较试验值高一些，主要由于试件在实际压缩过程中GFRP 格构腹板之间存在层间剥离现象，但在有限元模拟中，GFRP 被模拟成一个整体，忽略了此类破坏。

图13 波纹格构腹板试件荷载-位移曲线对比Fig. 13 Comparison between load-displacement curves of specimens with corrugated lattice web

2.3 参数分析

基于波纹腹板增强泡沫夹芯结构的有限元模型，选用试验阶段表现性能最优的结构TO-B100型试件进行有限元参数分析，主要包括腹板壁厚和泡沫密度两个参数。其中，腹板壁厚的参数分析是保证芯材的密度不变(ρ=40 kg/m3)，改变其腹板壁厚为1.2 mm、2.4 mm、3.6 mm，得到三个试件TO-B100-F1、TO-B100-F2、TO-B100-F3。

泡沫密度的参数分析是保证腹板壁厚不变(t=1.2 mm)，改变其泡沫密度为40 kg/m3、60 kg/m3、80 kg/m3，得到三个试件TO-B100-F1、TO-B100-F1-d60、TO-B100-F1-d80。图14 给出了试件腹板壁厚和泡沫密度参数分析的荷载-位移曲线。

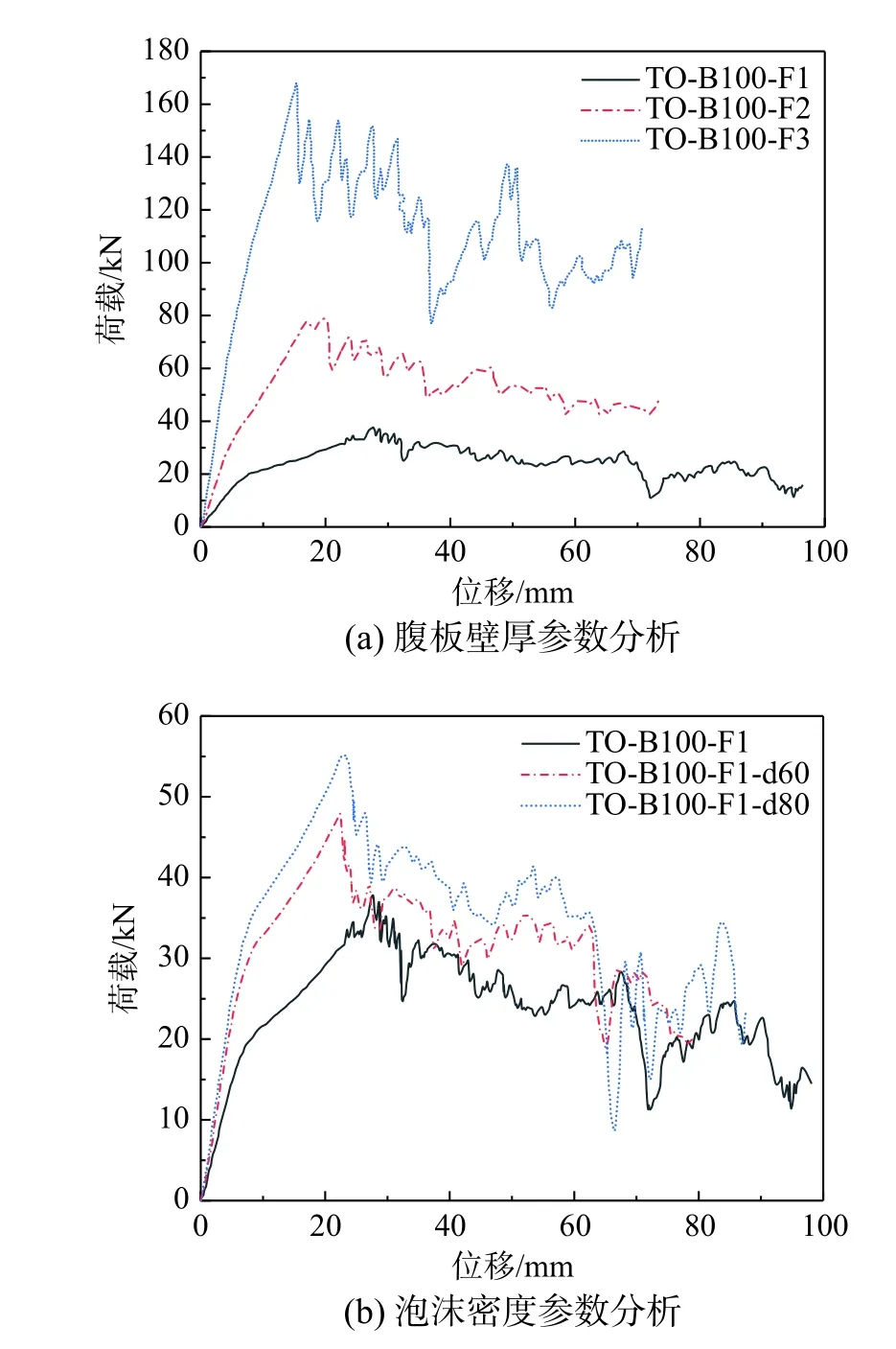
图14 不同参数试件的荷载-位移曲线Fig. 14 Load-displacement curves of specimens with different parameters

由图14 和表8 可知，腹板壁厚和泡沫密度对试件的影响较大。其中，随着腹板壁厚的增加，承载力上升段的最大值在增大，而上升段位移不断减小。当腹板壁厚从1.2 mm 分别增加至2.4 mm和3.6 mm 时，承载力上升段最大值从34.79 kN 分别变为79.04 kN 和118.46 kN，上升幅度分别为127.2%和240.5%；上升段位移则从24.43 mm 分别降至19.92 mm 和15.36 mm，下降幅度分别为18.5%和37.1%。相比之下，泡沫密度较腹板壁厚对试件的影响较小。泡沫密度越大，试件承载力越大。当泡沫密度从40 kg/m3变为60 kg/m3和80 kg/m3时，承载力上升段最大值从34.79 kN 分别提升至39.21 kN 和48.77 kN，上升幅度分别为12.7%和40.2%；位移上升段从24.43 mm 分别降低至22.88 mm 和21.33 mm，下降幅度分别为6.4%和12.7%。

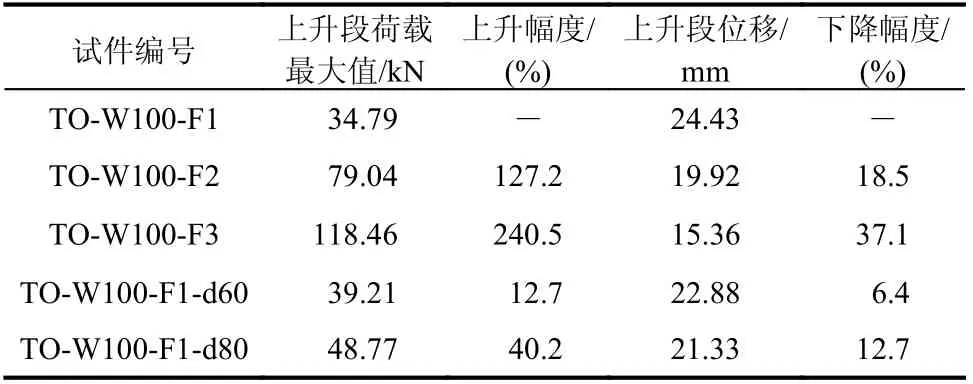
表8 准静态压缩参数分析Table 8 Parameter analysis of quasi-static compression

3 结论

本文以波纹腹板增强泡沫夹芯复合材料结构为研究对象，旨在研究其承载性能和吸能特性。通过对波纹腹板增强泡沫夹芯复合材料结构进行准静态压缩试验，得到其破坏模式和荷载-位移曲线，并运用ANSYS/LS-DYNA 对准静态压缩试验进行了数值模拟，主要结论如下：

(1)双层腹板夹芯结构的破坏模式主要表现为底层泡沫撕裂和格构腹板层间剥离。而三层腹板夹芯结构的破坏模式主要为格构腹板层间剥离和水平格构腹板弯曲变形两种，且三层腹板夹芯结构的破坏模式较理想。

(2) TO-B100-F2 试件吸能特性最优。能量吸收值最高的TO-B100-F2 试件较最低的TO-B150-F1试件高出163%；同时，试件TO-B100-F2 的比吸能和平均压溃力也最优，较最低的试件TO-B150-F1分别高出78%和163%。

(3)对试件准静态压缩试验开展了数值模拟研究，其结果表明：在压缩上升段，试件承载力模拟值与试验值吻合较好，误差均在20%之内，但上升段位移模拟值与试验值存在一定差距，原因在于简化建模导致了试件的刚度增大。此外，由参数分析可知，波形腹板壁厚对试件的准静态压缩承载力和吸能值存在显著影响，而泡沫密度的影响较小。