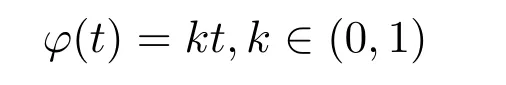模糊距离空间上非线性ĆiriĆ型拟压缩不动点定理

张建英,贺飞,路宁

(内蒙古大学数学科学学院,内蒙古 呼和浩特 010021)

1 引言和预备知识

文献[1]引入了拟压缩映射的概念,并建立了距离空间上的拟压缩映射不动点定理,后人称之为ĆiriĆ型拟压缩不动点定理.这一结果是最一般的压缩映射不动点定理之一,之后许多学者讨论了各类空间上的拟压缩不动点定理[2-10].特别地,文献[4]研究了距离空间上的非线性ĆiriĆ型拟压缩不动点定理,改进了许多形式的ĆiriĆ型拟压缩的结果.另一方面,文献[11]引入了模糊距离空间的概念,并且在此类空间上建立了一些不动点定理,之后许多学者研究了模糊距离空间的性质及该空间上的不动点定理[12-20].

本文将文献[4]在距离空间上的非线性ĆiriĆ型拟压缩不动点定理推广到了模糊距离空间,并且所得定理中的非线性函数类更广.

下面回顾一些基本概念.本文中R+=[0,+∞),R=(−∞,+∞),N={0,1,2,···},N+={1,2,···}.

定义 1.1[18]设函数η:R→[0,1].记η的α-水平集为[η]α={q∈R:η(q)≥α}.若满足

(1)存在q0∈R,使得η(q0)=1;

(2)对于任意的α∈(0,1],[η]α=[λα,ρα]是 R 中闭区间,其中

则称η是模糊实数.

由所有模糊实数组成的集合记为F.若对于η∈F满足对任意的q<0,使得η(q)=0,则称η是非负模糊实数.由所有非负模糊实数组成的集合记为F+.

定义 1.2[11]设X是非空集合,函数d:X×X→F+,L,R:[0,1]×[0,1]→[0,1]是两个非负对称函数,且满足L(0,0)=0,R(1,1)=1.对于任意的α∈(0,1]和所有的x,y∈X,记

若满足

(D1)d(x,y)=当且仅当x=y;

(D2)对于任意x,y∈X,d(x,y)=d(y,x);

(D3)对于任意x,y,z∈X,

(D3L)当p≤λ1(x,z),q≤λ1(z,y)且p+q≤λ1(x,y)时,满足

(D3R)当p≥λ1(x,z),q≥λ1(z,y)且p+q≥λ1(x,y)时,满足

则称d是模糊距离,且称(X,d,L,R)为(Kaleva-Seikkala型)模糊距离空间.

注 1.1距离空间可以看作特殊的模糊距离空间[11].

引理1.1[19]d(x,y)=当且仅当对于任意的t∈(0,1],ρt(x,y)=0.

由定义1.2与引理1.1可知,x=y当且仅当对于任意的t∈(0,1],ρt(x,y)=0.

引理 1.2[20]设(X,d,L,R)是模糊距离空间.记

(R-1)R(a,b)≤max{a,b};

(R-2)任意t∈(0,1],存在s∈(0,t],使得对任意r∈(0,t),有R(s,r)

则(R-1)⇒(R-2)⇒(R-3).

注 1.2引理1.2的蕴含关系反过来均不成立[15].

引理 1.3[15]设(X,d,L,R)是模糊距离空间,则下述结论成立:

(i)(R-1)⇒对任意t∈(0,1],x,y,z∈X,有

(ii)(R-2)⇒对任意t∈(0,1],存在s=s(t)∈(0,t],使得对任意x,y,z∈X,有

(iii)(R-3)⇒对任意t∈(0,1],存在s=s(t)∈(0,t],使得对任意x,y,z∈X,有

引理 1.4[15]设(X,d,L,R)是模糊距离空间,且满足(R-3).设

则集族{U(ε,α):ε>0,α∈(0,1]}构成了X×X上的一组 Hausdorff一致结构基.由集合

组成的集族构成了X×X上的一组Hausdorff拓扑基,而且该拓扑是可度量的.

定义 1.3[15]设(X,d,L,R)是模糊距离空间,{xn}⊂X,x∈X,

当n,m≥N时,ρt(xn,xm)<ε,则称{xn}是Cauchy列;

(iii)如果X中的每个Cauchy列都收敛,则称(X,d,L,R)是完备的模糊距离空间.

引理1.5[15]设(X,d,L,R)是满足(R-2)的模糊距离空间,则对于任意的t∈(0,1],ρt(x,y)在积空间X×X上连续.

下面介绍两类非线性函数,其中一类是文献[4]中提出的,另一类是本文定理中用到的条件更弱的非线性函数:

2 主要结果

注 2.1令φ(t)=kt,k∈(0,1),显然φ∈Φ,可得一般的压缩映射不动点定理.因此,本定理是一般压缩映射不动点定理的推广.当非线性函数φ取成

时,压缩系数便小于1了.

显然,由注1.1和定理2.1可得在距离空间(X,d)上,带有非线性函数φ∈Φ的不动点定理.由注1.3和定理2.1可得,如果存在ψ∈Ψ满足定理2.1的条件,那么f有唯一的不动点,并且由此可得如下结果:

推论 2.1设(X,d)是完备的距离空间,f是X上的自映射.如果存在ψ∈Ψ满足对于任意的x,y∈X,都有

那么f有唯一的不动点.

注 2.2[4]推论2.1就是文献[4]中的定理2.2的单映射形式.因此本文的结果将文献[4]的主要结果推广到了模糊距离空间.