基于一类迭代方程可微性解存在探讨

胡国兴

(合肥幼儿师范高等专科学校，安徽 合肥 230013)

0 引言

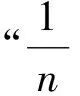
1 基本概念和相关引理

1.1 基本概念

不动点是一个函数术语，在数学中是指“被一个函数映射到其自身一个点”。用数学语言描述为:给定函数f:R→R，如果x∈R使f(x)=x，称x为f的一个不动点。一般地，若y=f(u),又u=g(x)，则函数y=f(g(x))叫x的复合函数[5]，其中y=f(u)叫外层函数，u=g(x)叫内层函数，x为自变量，y为因变量，u为中间变量。函数f和g的复合运算也可简单写作f∘g。简言之:复合函数就是把一个函数中的自变量换成另一个函数所得的新函数。复合函数也可以由多个函数相继复合而成。

迭代[6]即重复执行一系列运算步骤,从前面的量依次求出后面的量的过程。此过程的每一次结果,都是由对前一次所得结果施行相同的运算步骤得到的。用数学语言描述为：设I是任意一个区间,函数f:I→I，将f反复地复合，产生f2(x)=f∘f(x)，f3(x)=f∘f∘f(x)。一般地，fn(x)=f∘fn-1(x)(n≥3)。则fn为f的第n次迭代。设函数φ在点t处可导，函数f在点x=φ(t)处可导，那么复合函数f∘φ在点t处可导，并且(f∘φ)′(t)=(f′∘φ(t))φ′(t)，即称为复合函数求导的链式法则。

1.2 相关引理

引理1[6]若f∘f有唯一的不动点, 则f也有唯一的不动点。

证明设函数f∘f有唯一的不动点a,即f∘f(a)=a。再设f(a)=b,则f(b)=f∘f(a)=a,f∘f(b)=f(a)=b,所以b也是f∘f的不动点,又因为f∘f有唯一的不动点,故b=a。从而f(a)=a,即a是f的不动点。如果f还有不动点c,则f∘f(c)=c,则c也是f∘f的不动点,由唯一性得c=a,所以a是f唯一的不动点。

引理2[6]设f:R→R,若f∘f有且仅有两个不动点a,b(a≠b),只有以下两种情况：1)a,b都是f的不动点;2)f(a)=b,f(b)=a。

证明1)如果a,b都是f的不动点,它们显然也是f∘f的不动点。

2)如果不是1)的情况,则a,b中必有一个不是f的不动点。不妨设a不是f的不动点,令f(a)=c≠a，由于f(c)=f(f(a))=a,f∘f(c)=f(a)=c。这就说明c也是f∘f的不动点。由于c≠a,因此必有c=b，由此即得f(a)=b,f(b)=a。

引理3 设f:R→R,若f∘f有且仅有三个不动点a,b,c(a≠b≠c),只有以下四种情况：

1)a,b,c都是f的不动点

2)f(a)=b,f(b)=a,f(c)=c

3)f(a)=a,f(b)=c,f(c)=b

4)f(a)=c,f(b)=b,f(c)=a

证明1)如果a,b,c都是f的不动点,它们显然也是f∘f的不动点。

2)若f(a)=b，则f(b)=a，由于(f∘f)(f(c))=f(f∘f(c))=f(c)。所以f(c)也是f∘f的不动点，因此f(c)必等于a,b,c之一。但显然f(c)=a或f(c)=b都会导致矛盾，从而必有f(c)=c。即f(a)=b,f(b)=a,f(c)=c。

3)同理，若f(b)=c，则f(c)=b,从而必有f(a)=a。

4)同理，若f(a)=c，则f(c)=a,从而必有f(b)=b。

2 迭代方程可微性解存在性分析

2.1 映射g有一个不动点的情形

定理1 若g只有唯一不动点a,且g′(a)<0,则f∘f=g无可微解。

证明假定存在可微函数f使得f∘f=g,则由引理1知f也有唯一的不动点，即f(a)=a。按复合函数微商法则，得[f′(a)]2=f′(f(a))·f′(a)=(f∘f)′(a)=g′(a)<0，显然这是不可能成立的。故f∘f=g无可微解。

例1 在R上不存在可导函数f,使其满足f∘f(x)=-x3+x2+1。

证明事实上，对于函数g(x)=-x3+x2+1,g(x)-x=-(x-1)(x2+1)，显然g(x)-x=0只有一个实根，这表明g(x)只有唯一的不动点x=1。又g′(x)=-3x2+2x，故g′(1)=-1<0，由此可见g(x)满足定理1的条件，从而结论得证。

2.2 映射g有两个不动点的情形

定理2 若函数g恰有两个不动点a,b且1)g′(a)≠g′(b);2)g′(a)<0或g′(b)<0，则f∘f=g无可微解。

证明假定存在可微函数f使得f∘f=g，则由引理2有以下两种情况：

1)f(a)=a,f(b)=b

2)f(a)=b,f(b)=a

首先考虑第一种情况，按复合函数微商法则，可以得到

[f′(a)]2=f′(f(a))·f′(a)

=(f∘f)′(a)=g′(a)<0

或 [f′(b)]2=f′(f(b))·f′(b)=(f∘f)′(b)

=g′(b)<0

显然这是不可能的，故f∘f=g无可微解。

然后看第二种情况，按复合函数微商法则，有

g′(a)=f′(f(a))·f′(a)=f′(b)·f′(a)

g′(b)=f′(f(b))·f′(b)=f′(a)·f′(b)

由此得g′(a)=g′(b)，与题设g′(a)≠g′(b)矛盾。故f∘f=g无可微解。

例2 在R上不存在可导函数f,使其满足f∘f(x)=x2-3x+3。

证明事实上，对于函数g(x)=x2-3x+3，g(x)-x=(x-1)(x-3)，显然g(x)-x=0有两个实根,这表明g(x)有两个不动点x=1，x=3。又g′(x)=2x-3，故g′(1)=-1<0,g′(3)=3>0。由此可见g(x)满足定理2的条件，从而结论得证。

2.3 映射g有三个不动点的情形

定理3 若函数g恰有三个不动点a,b,c且g′(c)<0;g′(c)≠g′(b);g′(c)≠g′(a)，则f∘f=g无可微解。

证明假定存在可微函数f使得f∘f=g,则由引理3有以下四种情况：

1)f(a)=a,f(b)=b,f(c)=c

2)f(a)=b,f(b)=a,f(c)=c

3)f(a)=a,f(b)=c,f(c)=b

4)f(a)=c,f(b)=b,f(c)=a

先考虑前两种情况，按复合函数微商法则，得到

[f′(c)]2=f′(f(c))·f′(c)=(f∘f)′(c)

=g′(c)<0

这是不可能的，故f∘f=g无可微解。

然后看第三种情况，按复合函数微商法则，有

g′(b)=f′(f(b))·f′(b)=f′(c)·f′(b)

g′(c)=f′(f(c))·f′(c)=f′(b)·f′(c)

由此应有g′(c)=g′(b)，与题设g′(c)≠g′(b)矛盾。故f∘f=g无可微解。

最后看第四种情况，按复合函数微商法则，有

g′(a)=f′(f(a))·f′(a)=f′(c)·f′(a)

g′(c)=f′(f(c))·f′(c)=f′(a)·f′(c)

由此应有g′(c)=g′(a)，与题设g′(c)≠g′(a)矛盾。故f∘f=g无可微解。

例3 在R上不存在可导函数f,使其满足f∘f(x)=-x3+5x2-5x。

证明对于函数g(x)=-x3+5x2-5x，g(x)-x=-x3+5x2-6x=-x(x-2)(x-3)。显然g(x)-x=0有三个实根，这表明g(x)有三个不动点x=0，x=2，x=3。又g′(x)=-3x2+10x-5，故g′(0)=-5<0，g′(2)=3，g′(3)=-2。由此可见g(x)满足定理3的条件，从而结论得证。

例4 在R上不存在可导函数f,使其满足f∘f(x)=x3-5x2+3x+8。

证明函数g(x)=x3-5x2+3x+8，g(x)-x=x3-5x2+2x+8=(x+1)(x-2)(x-4)。显然g(x)-x=0有三个实根，这表明g(x)有三个不动点x=-1，x=2，x=4。又g′(x)=3x2-10x+3，故g′(-1)=16，g′(2)=-5<0，g′(4)=11。由此可见g(x)满足定理3的条件，从而结论得证。

3 结论

文章从可微函数f不存在这个方面讨论了一类迭代方程的可微解，得到这类方程可微解不存在的条件，利用这些条件可以很方便的判断出满足f∘f=g的可微函数f都不存在。从f∘f=g有一个不动点的情形开始讨论，逐渐推广到f∘f=g有二个和三个不动点的情形，并分别举例加以验证。然而对于很多的函数g，满足f∘f=g的可微函数f都不存在。一方面如何找到更多的函数g,满足f∘f=g的可微函数f都不存在；另一方面，能否找到这样一组条件，使得只要函数g满足这组条件，就一定存在函数f使f∘f=g，将是后续需要研究的课题。