Normal functions,normal families and uniformly normal families

Zhu Ting,Yang Liu

(School of Mathematics and Physics,Anhui University of Technology,Maanshan 243032,China)

Abstract：In this paper,the definition of the spherical derivative of meromorphic functions is extended to more general form concerning higher-order derivatives.By the wellknown Zalcman Lemma and the extended spherical derivative,we study the normality criteria for families of meromorphic functions.The theorems obtained extend Lappan′s five-point theorems and Marty′s criterion,and improve some previous results on normal functions and normal families.

Keywords：meromorphic functions,normal functions,normal family,spherical derivative,value distribution theory

1 Introduction

LetFbe a family of meromorphic functions on a domainD⊂C.ThenFis said to be normal onDin the sense of Montel,if each sequence ofFcontains a subsequence which converges spherically uniformly on each compact subset ofDto a meromorphic function which may be∞identically[1].By the famous normality criterion of Reference[2],a familyFof meromorphic functions onDis normal if and only if the family{f#:f∈F}of the corresponding spherical derivativesis locally uniformly bounded.

As to generalizations of Marty′s theorem to higher derivatives,Reference[3]obtained the following result.

Theorem 1.1Letkbe a natural number andFa family of functions meromorphic onDall of whose zeros have multiplicity at leastk.ThenFis normal if and only if the familyis locally uniformly bounded.

To simplify its statement,we use the following notation.For a meromorphic functionfinDand a positive integerk,the expression

represents an extension of the spherical derivative off.

Let∆rdenote the disc of radiusrin the complex plane.We will denote the unit disc by∆.Iffis a meromorphic function in∆,thenfis said to be normal if the set of functions{f◦T}forms a normal family in∆whereTranges over the conformal mappings of∆ onto∆.A necessary and sufficient condition for a functionfmeromorphic in∆to be normal in∆is that the real function

is bounded in∆[4].

Reference[5]posed the following interesting question:ifM>0 is given,does there exist a finite setEsuch that iffis meromorphic in∆then the condition that(1−|z|2)f#(z)≤Mfor eachz∈f−1(E)implies thatfis a normal function?In 1974,Reference[6]gave an affirmative answer to the question.

Theorem 1.2LetEbe any set consisting of five complex numbers, finite or in finite.Iffis a meromorphic function on∆such that

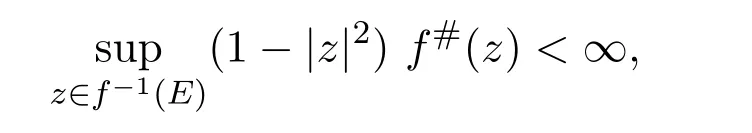
thenfis a normal function.

In the same paper,Lappan also commented on the sharpness of the number five in Theorem 1.2,showing that there are at least some cases in which “ five” can not be replaced by “four”.

Recently,for a meromorphic functionfin∆,Reference[7]considered not only the bound of the real function Φf(z)but also the bound of the spherical derivative off′and reduce the number five.

Theorem 1.3LetEbe any set consisting of four complex numbers, finite or in finite.Iffis a meromorphic function on∆such that

thenfis a normal function.

Note that iffis a normal function,then there exists a constantM(f)such that

for eachz∈∆.In general,the constantM(f)depends on the functionf.By the idea duce to Reference[8],Reference[9]gave the following.

Definition 1.1LetFbe a family of meromorphic functions in the unit disc∆.We call the familyFis uniformly normal on∆if

Theorem 1.4LetFbe a family of meromorphic functions in the unit disc∆such that all the zeros offinFare of multiplicity at leastk,and letEbe any set consisting ofk+4 complex numbers,finite or infinite.If

thenFis uniformly normal on∆.

Motivated by the accomplishment of Marty′s criterion and Lappan′s five-point theorem,many authors studied the problems relate to spherical derivative(see References[10-12]).Inspire by the results above,in this paper we prove the following.

Theorem 1.5LetFbe a family of meromorphic functions in the unit disc∆such that all the zeros offinFare of multiplicity at leastk,and letEbe any set consisting ofcomplex numbers,finite or infinite.If

thenFis uniformly normal on∆.Here and in the following,[x]denotes the greatest integer less than or equal tox.

Obviously,ifFis an uniformly normal family on∆,then each functionfinFmust be a normal function.Therefore,we obtain

Corollary 1.1Letfbe a meromorphic functions in the unit disc∆such that all of whose zeros have multiplicity at leastk,and letEbe any set consisting ofcomplex numbers,finite or infinite.If

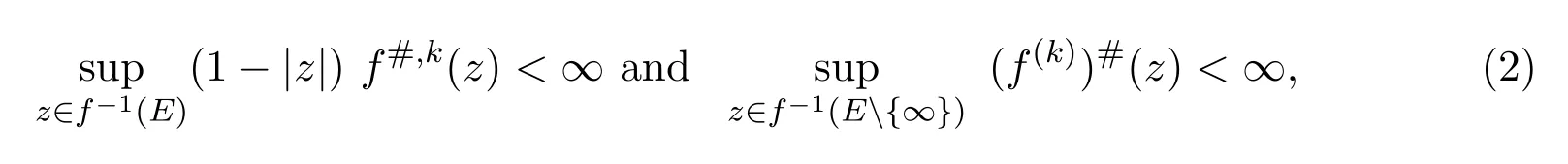
thenfis a normal function.

In addtion,takingk=1,we get the following corollary of Theorem 1.5 which is an improvement of Theorem 1.3.

Corollary 1.2LetFbe a family of meromorphic functions in the unit disc∆,and letEbe any set consisting of four complex numbers,finite or infinite.If

thenFis uniformly normal on∆.

An analogous for normal families of meromorphic functions is also obtained as follows.

Theorem 1.6LetFbe a family of meromorphic functions in the domainDsuch that all the zeros offinFare of multiplicity at leastk.Assume that for each compact subsetK⊂D,there exists a setE=E(K)be any set consisting ofcomplex numbers,finite or infinite.If

thenFis normal onD.

The plan of this paper is as follows.In Section 2,we state a number of auxiliary results.In Section 3,we give the proofs of theorems.

2 Lemmas

To prove our results,we require some lemmas.We assume the standard notation of value distribution theory.For details,see References[1,13-14].

Lemma 2.1[15](Zalcman′s Lemma)LetFbe a family of meromorphic functions of a domainDin C.IfFis not normal at a pointz0∈D,then there exist sequenceswithzn→z0,andwithϱn→0+,such that

converges uniformly on compact subsets of C to a nonconstant meromorphic functionF(ξ)of C.

Lemma 2.2[13-14](First Main Theorem) Suppose thatfis meromorphic in C andais any complex number.Then forr>0 we have

Lemma 2.3[13-14](Second Main Theorem) Suppose thatfis a non-constant meromorphic in C andaj(1≤j≤q)areq(≥3)distinct values inbC.Then

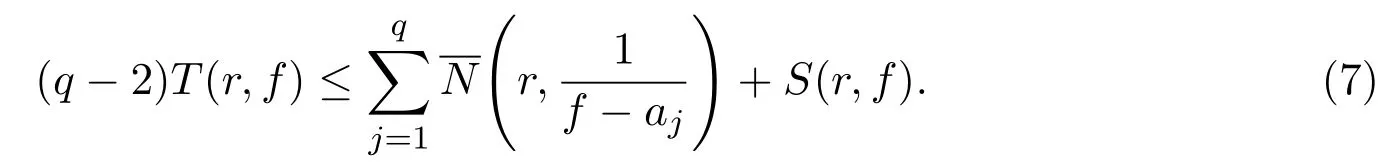
Lemma 2.4[13-14]Suppose thatfis a non-constant meromorphic in C andkis a positive integer.Then

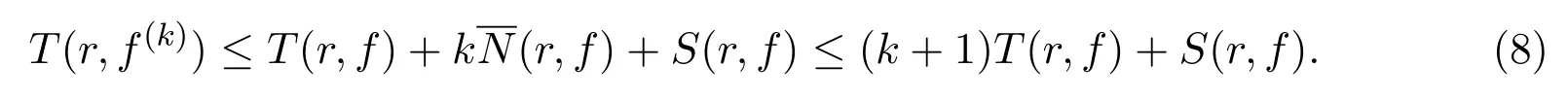
3 Proofs