平行机排序与转包问题的动态规划算法

陈荣军,唐国春

(1.常州工学院理学院,江苏 常州 213032;2.上海第二工业大学管理工程研究所,上海 201209)

1 引言

在现代工商业领域,转包策略正在被越来越广泛地应用.通过转包,制造商至少可以实现以下两个目的:一是实现产品按期交货.由于受自身生产能力、存储条件等限制,制造商往往无法在规定期限内完成生产任务,这时需要将部分订单转包给承包商加工,以提高自身对市场的响应能力;二是节约投资成本.由于产品往往由多道工序组成,需要不同的生产设备及技术.通过将部分工序转包,制造商可以将有限资源用于关键技术研发与重要设备更新,不仅提高了企业核心竞争力,还节约投资成本,降低因市场变化而带来的投资风险.当然,制造商因执行转包任务需要分出一定额度利润给承包商.为了实现自身利益的最大化,制造商往往需要同时考虑哪些工件或工序需要转包,哪些工件或工序自己加工,以及工件的加工次序,即排序.因此,研究转包策略具有非常重要的应用背景.

关于排序与转包的集成研究引起了许多学者的兴趣,在过去十多年里发表了一批相关研究成果,这些成果重点围绕制造商或承包商机器加工方式,转包费用以及工件运输方式等展开.下面重点介绍在平行机加工环境下的部分研究成果.

文献[1]等研究产品具有时间敏感性的排序与转包问题,假设制造商为平行机加工环境且承包商具有无限加工能力,目标是在工件最大完工时间不超过给定值情况下,极小化加工与转包费用和,设计启发式算法并分析了算法的渐进性能比.文献[2]等研究单阶段排序问题,假设工件既可以在内部制造商机器加工,也可以转包给外面的承包商加工.内部制造商有一个独立的平行机系统,而承包商有一台单机可以加工所有工件.研究内部加工工件和转包工件之集成排序,目标是极小化全部工件加工时间与转包费用和,提出了整数规划算法以及启发式算法,后者是将原问题分解为若干小且易解决的子问题并求出这些子问题的最优解.

文献 [3]等研究工件允许转包的单阶段平行机排序问题,目标是从可用的机器集(或承包商)中选出一些用于加工这些工件,目标是极小化若干费用函数.假设工件加工时间相同且分配给每台机器(或承包商)的工件数有一个上界和下界,分别研究了下界为0以及一般情形.文献[4]等研究平行机环境下的排序与转包问题,目标是极小化转包与延误费用和,他们设计了蚁群算法,并进行了数值试验.

文献 [5]研究平行机环境下工件排序与转包问题,基于人工团队过程算法 (简称TPA)设计了智能决策算法.同时,为了提高解的质量,在TPA每一迭代步设计了具有三种邻域结构的邻域搜索算法(简称NSA).此外,作者还用列排序算法(简称LS),GA,SA算法求解被研究问题,并对计算结果进行比较.同年,文献[6]研究平行机排序问题,目标是在工件最大延迟不超过给定值的情况下,极小化资源消耗与转包费用和,证明该问题在可中断情况下是多项式可解的,而在非中断情况下是强NP困难的,提出了分支定界算法及混合数学算法分别求得精确和近似解,并进行算法验证.

文献[7]研究n个单操作任务(或工件)要在m台平行机上加工的排序问题,且允许工件转包.当一台机器或承包商被选中加工工件时,需要付出一次性的固定费用;当一工件被一机器或承包商加工时,需要付出依赖于该机器或承包商的加工费用.目标是从m个空闲机器和(或)承包商中,选择k个机器和(或)承包商加工全部工件,极小化加工费用与固定费用和.证明了问题的NP困难性,并设计了有效的禁忌搜索算法,用中等规模实例进行验证.

除上述平行机加工环境外,近些年不少学者还研究了制造商为单机,自由作业,流水作业,异序作业等加工环境下的排序与转包问题[8-14],限于篇幅,本文不再详细阐述.

本文继续研究制造商是平行机环境的排序与转包问题,且假设承包商仅有一台单机.工件在制造商和承包商机器上所需的加工时间与费用均不同,且转包工件需要运回到制造商.本文需要确定转包工件集与全部工件加工顺序,分别极小化几个经典排序目标与转包费用和.本文余下部分是这样安排的:第2节介绍问题的模型及相关记号;第3-5节分别研究工件总完工时间,工件最大延误,误工工件数与转包费用和三个不同目标问题,分析问题困难性,并设计动态规划算法,最后第6节总结全文.

2 模型与符号

假设制造商有m台平行机{M1,M2,···,Mm},需要加工一批工件,记为

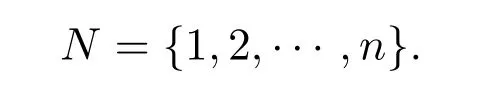
工件j∈N在制造商每台机器上需要加工时间pj,工期为dj.为了尽快完成加工任务,制造商常常要把部分工件转包给承包商加工.设承包商仅有一台单机,如果工件j∈N转包给承包商单机加工,需要加工时间αpj和加工费用βpj,其中α>0,β>0为常数.工件j被承包商加工后,即刻由专门工具运回制造商,但需要花费时间τ.

记Cj为工件j完工时间.如果工件j在制造商处加工,则它在平行机上完成加工的时刻即为Cj;否则,工件j在承包商处加工,将其运回至制造商的时刻称为完工时间.令Lmax=max{Lj,j∈N},其中Lj=Cj−dj,j∈N.置

本文研究哪些工件要在制造商平行机上加工,哪些工件要转包给承包商加工,以及工件在这些机器上的加工顺序即排序,使给定的目标函数最优.用传统三参数法[15]将本文问题记为m+1||λf+(1−λ)G,其中 “m+1”表示制造商有m台平行机,承包商有一台单机,为经典排序目标函数,G为工件总转包费用,λ∈[0,1]为常数.

定理 2.1是普通意义下NP困难的.

4 问题 m+1||λLmax+(1−λ)G

对问题m+1||λLmax+(1−λ)G,由问题 1||Lmax最优性,有性质4.1:

性质 4.1对问题m+1||λLmax+(1−λ)G,存在最优排序,在制造商及承包商机器上工件按EDD序加工.

根据性质4.1,设计动态规划算法,记DF 2,用于求解问题

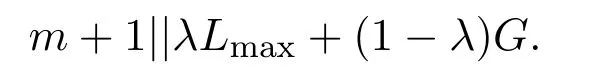
将全部工件按照EDD序重新编号,并记Aj={1,2,,···,j},j∈N.取(j,t1,t2,···,tm)为状态变量,其中tk为工件集Aj分配在机器Mk上工件加工总长.令L(j,t1,t2,···,tm)为在状态 (j,t1,t2,···,tm)下Lmax最优值.

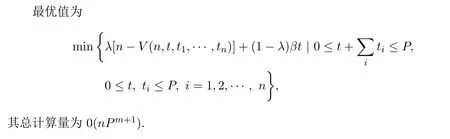
6 结束语

本文研究了制造商为平行机加工环境下的排序问题,且工件可以转包给仅有一台单机的承包商加工,分别为极小化工件总完工时间,最大延误,误工工件数与转包费用和的三个目标.本文分析了问题的NP困难性,并设计动态规划算法.对于其它复杂机器环境或者目标函数的问题,如何设计有效算法,值得继续研究.