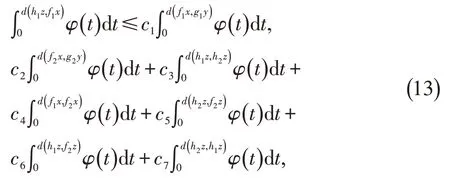W-空间上6个映射的公共不动点
2020-07-17高姗
高 姗
(太原工业学院理学系,山西太原 030008)
著名的Banach收缩原理[1]已经被广泛地推广和应用[2-8]。在W-空间上,通过引入两类3元实函数类,讨论了具有交换点的,满足隐式积分型收缩条件的2个和4个映射公共不动点的存在性和唯一性问题问题,t同时给出了3个映射和1个映射的公共不动点的存在性和唯一性定理[1-2]。通过引进一种6元实函数类,在W-空间上讨论具有交换点的反交换性质且满足积分型收缩条件的6个映射的唯一公共不动点存在问题。
1 准备知识
定义1设X是非空集合,如果一个映射d:X×X→R+满足d(x,y)=0 ⇔x=y,则称(X,d)为W-空间[9]。
定义2设f和g是W-空间(X,d)的两个自映射。称f和g是反交换的,如果x∈X,fgx=gfx,则fx=gx[10]。
定义3称x∈X是W-空间(X,d)的两个自映射f和g的交换点是指称f和g满足fgx=gfx[10]。
定义4Φ={φ|φ:R+→R+是满足在的任何紧子集上可积的,可求和的且对任何
定义5γ∈Γ 当且仅当(R+)7→R+,满足对任何a>0,b>0,由a≤γ(b,b),0,0,a,a,a推出a 定理1设(X,d)是W-空间,f1,f2,g1,g2,h1,h2:X→X是6个映射,(f1,f2),(g1,g2),(h1,h2)是具有交换点的反交换映射。如果对于任何x,y,z∈X,且满足当d(f1x,g1y)>0,d(g2y,h2z)>0,d(h1z,f1z)>0时, 其中φ∈Φ,γ,γ′,γ″∈Γ,则f1,f2,g1,g2,h1,h2有唯一公共不动点。 证明设u,v,w是(f1,f2),(g1,g2),(h1,h2)的交换点,即 则有 则由(1) : 则由γ的定义可知: 同理由(2),(3)可知: 则由(5),(6)可知 则(4)与(7)相矛盾,则d(f1u,g1v)>0,d(g2v,h2w)>0,d(h1w,f1u)>0里面必有一个不成立。 不妨假设d(f1u,g1v)>0不成立,即f1u=g1v,d(g2v,h2w)>0,d(h1w,f1u)>0,则(5),(6)成立。即(7)成立,从而 则 以下证明f1u是f1的不动点,否则有d(f1f1u,f1u)=d(f1f1u,g1v)>0, 则由(1), 从而f1u是f1的不动点。 又由f1f1u=f2f2u=f1f2u=f2f1u,可知f1u是f1,f2的公共不动点。同理,g1v是g1,g2的公共不动点,h1w是h1,h2的公共不动点。从而f1u是f1,f2,g1,g2,h1,h2的公共不动点。 若a,a′是f1,f2,g1,g2,h1,h2的两个公共不动点,对于(1) (2),令x=a,y=a′,z=a, 从而f1u是f1,f2,g1,g2,h1,h2的唯一公共不动点。 根据定理1可知如下结果。 定理2设(X,d)是W-空间,f1,f2,g1,g2,1,h2:hX→X是6个映射,(f1,f2),(g1,g2),(h1,h2)是具有交换点的反交换映射。如果对于任何x,y,z∈X,且满足当d(f1x,g1y)>0,d(g2y,h2z)>0,d(h1z,f1z)>0时, 其中φ∈Φ,a1+a2+a3+a4+a5+a6+a7<1,b1+b2+b3+b4+b5+b6+b7<1,c1+c2+c3+c4+c5+c6+c7<1。则f1,f2,g1,g2,h1,h2有唯一公共不动点。 证明定义γ∈Γ: 当a>0,b>0,且a≤γ(b,b,0,0,a,a,a)时,a≤a1b+a2b+a5a+a6a+a7a,则有从而γ∈Γ。 同理γ′∈Γ,γ″∈Γ。由定理1,f1,f2,g1,g2,h1,h2有唯一公共不动点。2 主要结果
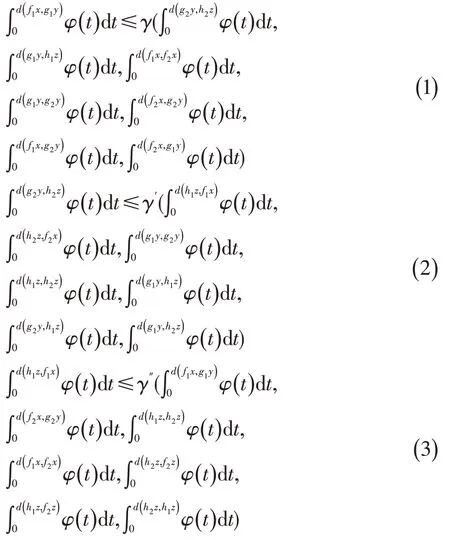





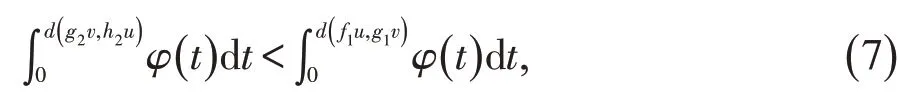

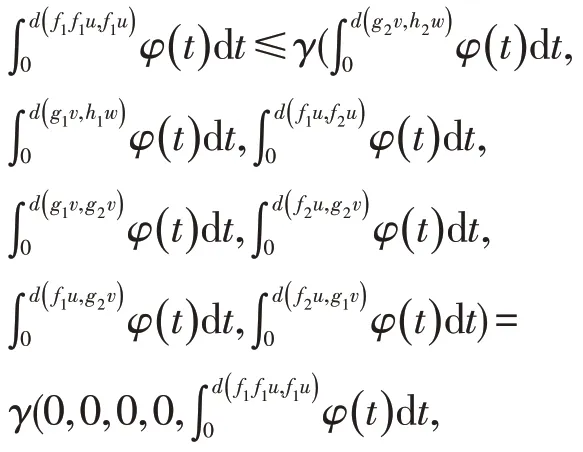


3 应用