求解变分不等式问题的一类新型算法及其应用

唐艳周海云荆平

(1.重庆工商大学数学与统计学院,重庆 400067;2.中国人民解放军陆军工程大学数学学院,河北 石家庄 050003;3.四川大学数学学院,四川 成都 610065)

1 引言

众所周知,变分不等式

是偏微分方程,网络平衡问题,互补性问题等非线性问题的核心,可应用于经济领域的均衡问题,运筹学问题及城市交通网络建模问题等.变分不等式(1)的解集通常记作V I(C,A).

在求解变分不等式(1)的过程中,人们提出了多种迭代算法,具体来看主要有两大类.一是投影法.Goldstein[1]首先提出了Goldstein-Levitin-Polyak投影方法:

其中PC是到C上Euclidean最小距离投影.假设算子A是Lipschitz连续强单调的,那么投影方法(2)收敛.1976年,在一般单调性假设下,Korpelevich[2]提出了外梯度投影方法:

该方法保证了序列的收敛性.但是,如果C是一般的闭凸集,方法(3)需要较高的计算成本.为此,Tseng[3]提出了一种新型梯度投影方法:

如果V I(C;A),则通过方法(4)生成的序列弱收敛到V I(C;A)中的某个元素.关于投影梯度法的更多细节和结果,还可以参考Thong和Hieu等人[4]的描述.

二是惯性算法.惯性法的描述来源于Alvarez和Attouch等[5]对二阶动力系统的重球法.受此思想的影响,Bot和Csetnek,Solodov等提出了惯性混合逼近迭代算法[6-8].此方法在一定程度上可以加快算法的收敛速度,目前已经受到了越来越多学者的关注.

虽然关于变分不等式(1)的研究已经获得了不少的成果,但在现实生活中,人们更倾向于寻找变分不等式(1)和非线性算子不动点问题的公共解,即,找到点u∈C使得

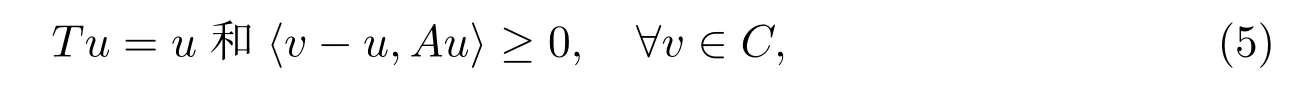
其中T:C→C是一个非线性算子,F(T)={x:Tx=x}是T的不动点集.

信号处理、经济规划、网络资源分配和图像恢复等均可以描述为问题(5).目前,关于问题 (5)的研究,主要集中在两点.一是非线性算子T的类型,从 Alakoya[9],Dong[10],Zhou[11-12]等众多文献构造的不同迭代算法来看,涉及的非线性算子主要为非扩张算子及拟非扩张算子;二是迭代算法的创新构造及收敛性分析.另外,大部分迭代算法生成的序列只得到弱收敛的结果.

因此,自然地提出了以下这个问题:(Q)能否建立新的方法更快更好地强收敛于更广义的非线性算子不动点问题与变分不等式问题的公共解呢？

受Thong[4],Alakoya[9],Dong[10],Gibali[13]等研究成果的启发,本文将继续致力于问题(5)的数值求解并对上面的问题给予肯定的回答.

2 预备知识

3 自适应步长惯性投影法

在这个部分,基于Tseng新型梯度投影方法和Halpern迭代算法,针对半压缩映射不动点问题与变分不等式问题的公共解问题,提出两个新的惯性型投影算法.另外,假设H是一个实Hilbert空间,C是H的非空闭凸子集.设A:H→H是单调Lipschitz连续算子.设T:H→H是一个τ-半压缩映射且0<τ<1.

半压缩映射不动点问题与变分不等式问题的公共解,是指,找到点u∈C使得

并记问题(8)的解集为

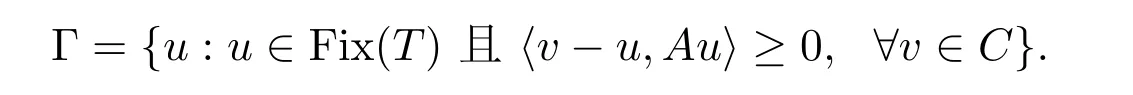
3.1 算法 3.1及弱收敛定理

由于Armijo搜索方法可以使步长不依赖于Lipschitz常数,因此在Tseng新型梯度投影方法和惯性型投影算法的基础上结合Armijo搜索方法提出了下面的算法3.1并研究了其弱收敛性.

3.2 算法 3.2及强收敛定理

由于算法3.1产生的序列只能弱收敛于问题的解,而在实际应用中,强收敛性的需求更为迫切.所以在这个部分,结合Tseng新型梯度投影方法,Halpern迭代算法和惯性型投影算法提出了下面的算法3.2,并对其强收敛性做了分析.

4 数值仿真及比较

为了评估本文算法的性能,将给出数值实验来进行仿真、演示和比较.

例 4.1本例中考虑一个Harker[17]等人研究过的互补问题,该问题也曾多次被其他学者仿真过,比如,Hieu[18]等.设算子A:Rm→Rm定义为Ax=Mx+q,其中q∈Rm.M=NNT+S而N是一个m×m矩阵,S是一个m×m斜对称矩阵.显然A是单调 Lipschitz连续的,其 Lipschitz常数L=∥M∥.设算子T:Rm→Rm定义为,则它为的半收缩映射.另设可行集C⊂Rm为C:={x∈Rm|∥x∥≤r},其中r是随机选择的半径.

本例将对算法3.1,算法3.2,Thong[4]的自适应Tseng外梯度法,Shehu[19]的次梯度 -外梯度粘性方法在ℓ=0.001,µ=0.1和ℓ=0.01,µ=0.2及m=20,50,100等不同情况下进行比较.本例设置Dk=∥xk+1−xk∥≤10−4作为停止标准.图1和表1列出了每种方法的收敛情况.

图1 算法3.1,算法3.2,Thong[4]算法及Shehu[17]算法,m=100.

表1 例1-数值结果

注 4.1从图1和表1可看出,因为本文提出的算法3.1,算法3.2加入了惯性项,所以收敛速度远高于文献[4,19]所列的算法;同时,基于相同的停机准则,本文的算法能够达到更高的精确度;另外,值得强调的是,相比文献[4,19]的单调算子,本文研究的伪单调算子可应用于解决更广泛的问题.综上,本文提出的算法3.1,算法3.2是可行的,也表明惯性算法在一定程度上会有更快更好的收敛结果.

5 结语

本文基于著名的测度投影算法和惯性算法,在Hilbert空间中给出了变分不等式问题与非线性算子不动点问题公共数值解的两种新迭代方法,并在一定的条件下,证明了算法的强、弱收敛性.另外,分别在有限维空间和无限维空间中进行了具体的数值仿真实验,其中包含互补问题的仿真实验数据,验证了所列出的算法的有效性和潜在的实用性.通过和已有的某些算法比较,可以看到,本文所列出的算法有两个优点:(1)适用于半压缩映射类,这类映射比现有文献中的非扩张映射,直接映射及拟伪压缩映射等非线性映射更为广义;(2)使用的步长不需要预先估算Lipschitz常数,这意味着收敛速度会更快.在后续研究中,将着力于空间的改进,例如在更一般的Banach空间上研究变分不等式问题的解.