完备的D -度量空间上具有收缩型条件映射族的唯一公共不动点
2015-12-26龚学徐佳宁吴凡朴勇杰
龚学, 徐佳宁, 吴凡, 朴勇杰
( 延边大学理学院 数学系, 吉林 延吉 133002 )
完备的D -度量空间上具有收缩型条件映射族的唯一公共不动点
龚学, 徐佳宁, 吴凡, 朴勇杰*
( 延边大学理学院 数学系, 吉林 延吉 133002 )
利用完备的D-度量空间上满足某种收缩条件的4个自映射S,T,I,J构造了具有唯一极限的序列,并证明了该序列的唯一极限即为S,T,I,J的唯一公共不动点,且由此得到了更为一般形式的无穷多个映射的唯一公共不动点定理,所得结果推广和改进了D-度量空间上的若干唯一公共不动点定理.
D-度量空间; 弱相容; 重合点; 公共不动点
1 基本概念及引理
1992年,B Dhage[1]引进了D-度量空间,并在该空间上得到收缩型映射的不动点定理.之后,文献[2-6]给出了若干满足收缩条件的一个映射的不动点定理和若干个映射的公共不动点定理,文献[7-8]分别给出了在D-度量空间上无穷多个映射的唯一公共不动点存在定理.
下面给出本文所需要的基本概念和引理.
定义1[7-8]设X是非空集合, D∶X×X×X→R+=[0,+∞)为映射.称(X,D)为D-度量空间,如果满足如下条件:
(i) D(x,y,z)=0 ⟺ x=y=z (重叠性);
(ii) 对任何x,y,z∈X, D(x,y,z)=D(u,v,w),∀{u,v,w}={x,y,z} (对称性);
(iii) 对任何x,y,z,a∈X, D(x,y,z)≤D(x,y,a)+D(x,a,z)+D(a,y,z).
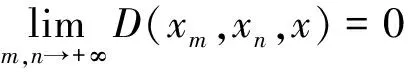
文献[2,7]中指出,如果D-度量关于两个变元是连续的,则收敛序列的极限是唯一的.本文假设D-度量关于两个变元是连续的.
定义3[9-10]设X是非空集合, f,g∶X→X是两个映射.如果存在x,w∈X使得w=f x=gx, 则称x是{f,g}的重合点, w是{f,g}的重合的点.
定义4[11]设X是非空集合, f,g∶X→X是两个映射.如果x∈X且fx=gx时, f g x=g f x成立,则称{f,g}是弱相容的.
引理1[7,12](D-柯西原理)设{xn}n∈N是D-度量空间X中具有D-有界数M的序列.如果对任何n,m∈N且m>n, 成立D(xn,xn+1,xm)≤αnM, 其中0≤α<1, 则{xn}n∈N必是D-柯西序列.
引理2[9-10]如果f,g∶X→X是弱相容的且有唯一的重合的点w=f x=gx, 则w是f和g的唯一公共不动点.
2 主要结果及其证明
定理1 设X是完备的具有D-有界数M的D-度量空间, S,T,I,J∶X→X是4个映射,使得SX⊂JX, TX⊂IX且I或J是满映射.假设对任何x,y,z∈X, 有
D(S x,Ty,z)≤q D(I x,Jy,z),
(1)
其中0≤q<1, 则{T,J}及{S,I}有相同的唯一重合的点.进一步,如果{T,J}及{S,I}分别是弱相容的,则{S,T,I,J}有唯一公共不动点.
证明 任选x0∈X.根据SX⊂JX及TX⊂IX可构造两个序列{xn}和{yn}满足
y2n=S x2n=Jx2n+1, y2n+1=Tx2n+1=I x2n+2, n=0,1,2,….
(2)
对任何固定的n及z∈X, D(y2n,y2n+1,z)=D(S x2n,Tx2n+1,z)≤q D(I x2n,Jx2n+1,z)=q D(y2n-1,y2n,z)=q D(S x2n,Tx2n-1,z)≤q2D(I x2n,Jx2n-1,z)=q2D(y2n-2,y2n-1,z)≤…≤q2nD(x0,x1,z)≤q2nM, 由此得到
D(y2n+1,y2n+2,z)=D(S x2n+2,Tx2n+1,z)≤q D(I x2n+2,Jx2n+1,z)=q D(y2n+1,y2n,z)≤q2n+1M.
综合上述两个结论可得到对任何n,p∈N,
d(yn,yn+1,yn+p)≤qnM.
(3)

假设J是满射,则存在v∈X使得u=Jv.对任何n,
D(u,Tv,u)≤D(y2n,Tv,u)+D(u,y2n,u)+D(u,Tv,y2n)=2D(S x2n,Tv,u)+D(u,y2n,u)≤
2q D(I x2n,Jv,u)+D(u,y2n,u)=2q D(y2n-1,u,u)+D(u,y2n,u).
令n→∞, 则上式右边的极限为0, 于是D(u,Tv,u)=0, 因此Tv=u=Jv, 即v是{T,J}的重合点, u是{T,J}的重合的点.
因为u=Tv∈TX⊂IX, 因此存在w∈X使得u=I w.对任何n,
D(S w,u,u)≤D(y2n+1,u,u)+D(S w,y2n+1,u)+D(S w,u,y2n+1)=
D(y2n+1,u,u)+2D(S w,Tx2n+1,u)≤D(y2n+1,u,u)+2q D(I w,Jx2n+1,u)=
D(y2n+1,u,u)+2q D(u,y2n,u).
令n→∞, 则上式右边的极限为0, 于是D(S w,u,u)=0, 因此S w=u=I w, 即w是{S,I}的重合点, u是{S,I}的重合的点.
假设z=S x=I x也是{S,I}的重合的点,则根据D(z,u,u)=D(S x,Tv,u)≤q D(I x,Jv,u)=q D(z,u,u)及q<1得到D(z,u,u)=0, 于是z=u.这说明u是{S,I}的唯一的重合的点.类似地,可证明u也是{T,J}的唯一的重合的点.
如果{T,J}及{S,I}分别是弱相容的,则根据引理2可知u是{T,J}及{S,I}的唯一公共不动点,于是u是{S,T,I,J}的一个公共不动点.显然, u是{S,T,I,J}的唯一公共不动点.
如果I是满映射,可类似地证得相同的结果,故本证明在此省略.
推论1 设X是完备的具有D-有界数M的D-度量空间, S,T∶X→X是2个映射.假设对任何x,y,z∈X,
D(S x,Ty,z)≤q D(x,y,z),
(4)
其中0≤q<1, 则{S,T}有唯一公共不动点.
证明 只需在定理1中取I=J=1X即可到推论1.
推论2 设X是完备的具有D-有界数M的D-度量空间, I,J∶X→X是两个满映射.假设对任何x,y,z∈X,
D(x,y,z)≤q D(I x,Jy,z),
(5)
其中0≤q<1, 则{I,J}有唯一公共不动点.
证明 只需在定理1中取S=T=1X即可到推论2.
注记1 如果在推论1中S=T及在推论2中I=J, 则推论1和推论2分别是Banach收缩原理和第一膨胀映射的不动点存在定理[13]在D-度量空间上的一种新的表现形式.

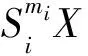
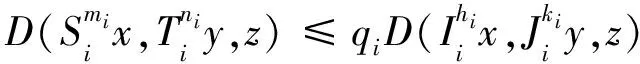
(6)
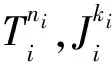
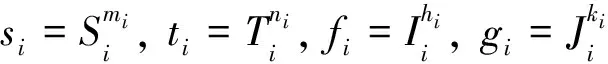
D(ui,ui,Siui)≤qiD(ui,ui,Siui),
于是得到Siui=ui.类似地,可得到Tiui=Iiui=Jiui=ui, 因此ui是{Si,Ti,Ii,Ji}的一个公共不动点.若vi是{Si,Ti,Ii,Ji}的公共不动点,则ui和vi都是{si,ti,fi,gi}的公共不动点,于是ui=vi.因此对每个i∈N, {Si,Ti,Ii,Ji}有唯一公共不动点ui.
设i,j∈N且i≠j.因为Siui=Tiui=Iiui=Jiui=ui, Sjuj=Tjuj=Ijuj=Jjuj=uj, 再结合F的弱可交换性可得
Sjui=SjSiui=SiSjui, Sjui=SjTiui=TiSjui, Sjui=SjIiui=IiSjui, Sjui=SjJiui=JiSjui.
这说明Sjui是{Si,Ti,Ii,Ji}的一个公共不动点,于是由{Si,Ti,Ii,Ji}的公共不动点唯一性得到Sjui=ui.类似地,可得到Tjui=ui, Ijui=ui, Jjui=ui.于是ui是{Sj,Tj,Ij,Jj}的一个公共不动点,由{Sj,Tj,Ij,Jj}的公共不动点的唯一性得uj=ui.令u*=ui, 则u*是F的一个公共不动点.显然, u*是F的唯一公共不动点.
[1] Dhage B. Generalized metric spaces and mappings with fixed points[J]. Bulletin of Calcutta Mathematical Society, 1992,84(4):329-336.
[2] Singh B, Jain S, Jain S. Semicompatibility and fixed point theorems in an unbounded D-metric space[J]. International Journal of Mathematics and Mathematical Science, 2005,2005(5):789-801.
[3] Dhage B, Arya S, Ume J. A general lemma for fixed point theorems involving more than two maps in D-metric spaces with applications[J]. International Journal of Mathematics and Mathematical Science, 2003,2003(11):661-672.
[4] Dhage B, Asha A, Kang S. On common fixed points of pairs of a single and a multivalued coincidentally commuting mappings in D-metric spaces[J]. International Journal of Mathematics and Mathematical Science, 2003,2003(40):2519-2539.
[5] Singh B, Jain S. Common fixed points of weak-compatible maps on D-metric space[J]. Journal of ChungCheong Mathematical Society, 2004,17(2):111-124.
[6] Singh B, Sharma R. Common fixed points via compatible maps in D-metric spaces[J]. Rad Mat, 2002,11(2):145-153.
[8] 沈京虎,朴勇杰.D-度量空间上一族拟收缩自映射的唯一公共不动点[J].延边大学学报:自然科学版,2014,40(1):8-10.
[9] Abbas M, Jungck G. Common fixed point results for noncommuting mappings without continuity in cone metric spaces[J]. Journal of Mathematical Analysis and Applications, 2006,341(1):416-420.
[10] Han Y, Xu S Y. New common fixed point results for four maps on cone metric spaces[J]. Applied Mathematics, 2011,2:1114-1118.
[11] Bari C D, Vetro P.φ-pairs and common fixed points in cone metric spaces[J]. Rendiconti del circolo Matematico Palermo, 2008,57:279-285.
[12] Dhage B. Some results on common fixed points-I [J]. Indian Journal of Pure and Applied Mathematics, 1999,30(8):827-837.
[13] 王尚志,李伯渝,高智民.膨胀映射及其不动点定理[J].数学进展,1982,11(2):149-153.
Unique common fixed points for a family of mappings with contractive type conditions on complete D-metric spaces
GONG Xue, XU Jianing, WU Fan, PIAO Yongjie*
(DepartmentofMathematics,CollegeofScience,YanbianUniversity,Yanji133002,China)
We use four self-mappings S, T, I, J satisfying some contractive conditions on complete D-metric spaces to construct a sequence which has a unique limit, and prove that the unique limit of the sequence is the unique common fixed point of S, T, I, J. Furthermore, we obtain a more general unique common fixed point theorem for an infinite family of self-mappings. The obtained results generalize and improve some unique common fixed point theorems on D-metric spaces.
D-metric space; weakly compatible; coincidence point; common fixed point
2014-12-23 基金项目: 国家自然科学基金资助项目(11361064)
1004-4353(2015)01-0001-04
O177.3; O189.11
A
*通信作者: 朴勇杰(1962—),男,理学博士,教授,研究方向为非线性分析和不动点理论.
