线性亚苯基系统的强迫和反强迫多项式
2023-01-02邓凯
邓 凯
(北方民族大学 数学与信息科学学院,宁夏银川 750027)
§1 引言
设G是一个无向图,V(G)和E(G)分别表示图G的顶点集和边集.图G中任一没有公共端点的边集合或独立边集合,称作是图G的一个匹配,覆盖了图G的所有顶点的匹配叫做图的完美匹配.完美匹配在资源优化安排,理论化学中Kekul´e结构,统计力学中Dimer模型等方面都有重要的应用,是图论中一个基本的研究对象.文献[1]系统的总结了匹配理论的发展结果.
图的完美匹配强迫问题源自理论化学研究.化学实验证实稳定的苯类碳氢化合物中碳碳双键的集合是其分子图中的一个完美匹配,化学家称其为Kekul´e结构.1987年,Klein和Randi´c[2]发现共轭分子中一个Kekul´e结构的部分双键固定后其它双键的分配是唯一确定的,他们将确定一个Kekul´e结构所需固定的最少双键数目称为该Kekul´e结构的内自由度.1991年,Harary等[3]将共轭分子图上Kekul´e结构的内自由度概念拓展到一般图的完美匹配上,称为完美匹配的强迫数.
设M是图G的一个完美匹配,子集S ⊆M称作是M的强迫集,如果S不被G中其它完美匹配所包含,也就是说,S作为M的内部子结构决定了M.M的最小强迫集的势称作M的强迫数,记为f(G,M).图G的所有完美匹配强迫数的最小值和最大值分别称为G的最小强迫数和最大强迫数,分别记为f(G)和F(G).完美匹配强迫数的计算十分困难,Adams等[4]证明了求解最大度为3的二部图中完美匹配的强迫数是NP-完全的,Afshani等[5]进一步证明了求解最大度为4的二部图的最小强迫数是NP-完全的,而图的最大强迫数的计算复杂性仍然未知.徐丽琼,边红和张福基[6]证实了六角系统的最大强迫数等于其Clar数,六角系统是苯类碳氢化合物的分子图,Clar数是六角系统中最多可能的共振苯环个数,反映了分子的稳定性.
图中完美匹配数目通常是指数多的,实际上一般图的完美匹配计数问题是#P-完全的[1].一个自然的问题是图中所有完美匹配的强迫数如何分布? Adams等[4]首先提出了图G的强迫谱,它是G中所有完美匹配强迫数的集合(不考虑重数),记为Specf(G).进一步考虑强迫谱中强迫数的重数是对强迫数分布的完整研究,为此张和平等[7]定义了图G的强迫多项式

其中w(G,i)表示图G中强迫数等于i的完美匹配数目.
设M(G)表示图G中所有完美匹配的集合,M是图G的一个完美匹配,则公式(1)可改写为

图的强迫多项式完整地反映了完美匹配强迫数的分布情况,蕴含了图的完美匹配计数,图的强迫谱,强迫数的重数计算等困难问题.目前仅有一些零星的特殊图类的强迫多项式是已知的,例如cata-型六角系统[7],平行四边形六角系统[8],方格子图P3×P2k[9],芘系统[10]等.
2007年,Vukiˇcevi´c和Trinajsti´e[11]从完美匹配强迫问题的反面考虑,提出了图的反强迫数,它是从图中删边使得到的图有唯一的完美匹配所需要删除的最少边数.Klein与Rosenfeld[12],雷洪川,叶永南与张和平[13]分别以不同的方式,进一步提出了单个完美匹配的反强迫数.设M是图G的一个完美匹配,子集S′ ⊆E(G)M称作是M的反强迫集,如果M是图G −S′中唯一的完美匹配,也就是说,S′从M的外部确定了M.M的最小反强迫集的势称作M的反强迫数,记为af(G,M).图G中所有完美匹配强迫数的最小值和最大值分别称为G的最小反强迫数和最大反强迫数,分别记为af(G)和Af(G).因此,图的反强迫数就是图的最小反强迫数.邓凯与张和平[14]证明了确定最大度为4的二部图中完美匹配的反强迫数是NP-完全问题,而图的最小和最大反强迫数的计算复杂性仍然未知.六角系统的最大反强迫数也被证实等于其Fries数[13],Fries数是六角系统中最多可能的交错六角形的个数,它也是反映分子稳定性的指标.
图G的反强迫谱定义为G中所有完美匹配反强迫数的集合,记作Specaf(G)[13].反强迫多项式[15]的概念也被提出,它是反映图G中所有完美匹配反强迫数分布的计数多项式,定义为

其中u(G,i)表示图G中反强迫数等于i的完美匹配数目.
公式(3)可改写为
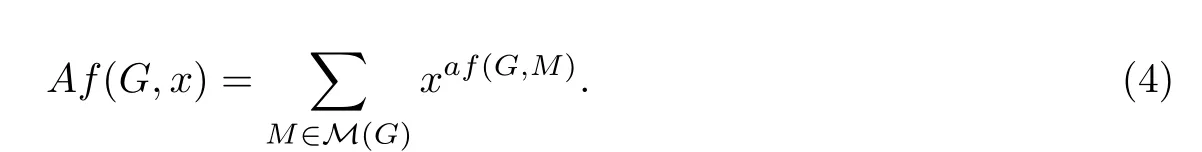
目前仅有几类特殊图的反强迫多项式是已知的,例如最小强迫数为1的极值六角系统[15],平面方格子图P3×P2k[9],芘系统[10]等.
本文将计算线性亚苯基系统的强迫多项式和反强迫多项式,并给出它们精确的表达式.
§2 预备知识
亚苯基系统是由苯环和环丁二烯交错构成的[16],其分子图由六边形和四边形交替串联生成,其中六边形仅与四边形相邻,且一个四边形恰好与两个六边形相邻.内对偶图是一条直线段的亚苯基系统叫做线性亚苯基系统,含有n个苯环的线性亚苯基系统记为Ln(见图1).

图1 含有n个苯环的线性亚苯基系统Ln
设M是图G的一个完美匹配,G中的一个圈C称作是M-交错圈,如果C中的边在M和E(G)M中交替出现.设Φ(Ln)表示线性亚苯基系统Ln中完美匹配数目,则有下面的递推关系.
定理2.1Φ(Ln)=2Φ(Ln−1)+Φ(Ln−2),其中n ≥2,Φ(L0)=1,Φ(L1)=2.
证L0代表空图,可定义Φ(L0)=1.L1表示一个苯环,所以Φ(L1)=2.当n ≥2时,设M ∈M(Ln),分两种情形讨论(见图1).
情形1Ln中左边第一个六边形h1是M-交错圈.从Ln中删去h1的6个顶点,得到一个含有n−1个苯环的线性亚苯基系统Ln−1.此时M在Ln−1上的限制是Ln−1的一个完美匹配,且h1形成M-交错圈的方式有2种,所以这类完美匹配的个数为2Φ(Ln−1).
情形2h1不是M-交错圈.此时{v3v4,u3u4} ⊆M,且由六边形h1,h2和四边形s1生成的线性亚苯基L2的边界是M-交错圈.从Ln中删去h1,h2的12个顶点,得到一个含有n −2个苯环的线性亚苯基系统Ln−2,且M在Ln−2上的限制是Ln−2的一个完美匹配,所以这类完美匹配的个数为Φ(Ln−2).
综上所述,线性亚苯基系统Ln中完美匹配数目Φ(Ln)=2Φ(Ln−1)+Φ(Ln−2).
利用定理2.1的递推关系,容易得到下面的显式表达式.
推论2.1Φ(Ln)=
令c(M)表示图G中相互不交M-交错圈或独立M-交错圈的最大个数.Pachter和Kim证明了下面的极大极小定理.
定理2.2[17]设G是平面二部图,M是G的一个完美匹配,则f(G,M)=c(M).
平面图的一个内面的边界称作是面圈,张和平与张福基证明了下面的结论.
定理2.3[18]设M是平面基本二部图G的一个完美匹配,C是G的一个M-交错圈,则C的内部包含一个M-交错面圈.
推论2.2设M是线性亚苯基系统Ln的一个完美匹配,则存在一个势最大的独立M-交错圈集合A,且A中仅包含面圈.
证设A是Ln中一个势最大的独立M-交错圈集合,且A中包含尽可能多的面圈,则A中仅包含面圈.假设A包含一个非面圈C,即C既不是六边形也不是四边形.Ln是平面基本二部图,根据定理2.3,C的内部包含一个面圈f.因为Ln是外平面图,所以A中任意两个M-交错圈一个不能在另一个的内部.因此(A{C})∪{f}也是一个势最大的独立M-交错圈集合,但是它所包含的面圈比A多一个,这与A中包含面圈个数的最大性矛盾.
线性亚苯基的面圈只能是六边形或四边形,根据定理2.2和推论2.2,可直接得到下面的推论.
推论2.3设M是线性亚苯基系统Ln的一个完美匹配,则M的强迫数等于不交的M-交错六边形和M-交错四边形的最大个数.
设M是图G的一个完美匹配,G中的两个M-交错圈称作是相容的,如果它们不交或仅交于M中边.令c′(M)表示G中最多可能的相容M-交错圈的个数,对平面二部图有下面的极大极小定理.
定理2.4[13]设M是平面二部图G中的一个完美匹配,则af(G,M)=c′(M).
设M是平面图G中的一个完美匹配,M-交错圈集A′称作是相容的,如果A′中任意两个M-交错圈都是相容的.相容M-交错圈集A′中两个圈C1和C2称作是交叉的,如果C1和C2有一条M中的公共边e,且C1经由边e进入C2的内部.如果A′中任意两个圈都不是交叉的,那么称其为非交叉的相容M-交错圈集.例如,图2中的粗边集合M是亚苯基L2的一个完美匹配,M-交错圈C1:=v1v2v3v4u4u3u2u1v1和C2:=v3v4v5v6u6u5u4u3v3是两个交叉的相容M-交错圈,而L2的边界和四边形s是两个非交叉的相容M-交错圈.文献[13]中定理3.1的证明引入了把六角系统的交叉相容交错圈集转化为势相同的非交叉相容交错圈集的方法,文献[19]指出该方法对平面二部图也成立,结合定理2.4,有下面的推论.
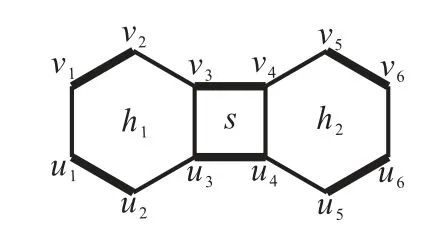
图2 亚苯基L2,粗边的集合是一个完美匹配
推论2.4设M是平面二部图G的一个完美匹配,A′是势最大的非交叉相容M-交错圈集,则af(G,M)=|A′|.
为了叙述方便,下面将形如图2中亚苯基L2的边界交错圈称为L2-型交错圈.
推论2.5设M是线性亚苯基系统Ln的一个完美匹配,则Ln中有一个势最大的非交叉相容M-交错圈集A′,且A′中的圈要么是面圈,要么是L2-型交错圈.
证设A′是Ln中势最大的非交叉相容M-交错圈集,且包含尽可能多的面圈和L2-型交错圈,则A′中的圈要么是面圈,要么是L2-型交错圈.假设C′ ∈A′是一个非面圈,根据定理2.3,C′的内部包含一个M-交错面圈s.如果C′与s不相容,那么(A′{C′})∪{s}仍然是Ln的一个势最大的非交叉相容M-交错圈集,但是它比A′多包含1个面圈,与A′包含面圈个数的最大可能性矛盾.因此C′与s必然相容,所以s是一个四边形,且s与相邻的两个六边形h1和h2生成的一个亚苯基L2的边界B(L2)是L2-型交错圈,如图2所示.我们断言C′=B(L2),否则(A′ {C′})∪{B(L2)}仍然是Ln的一个势最大的非交叉相容M-交错圈集,但是它比A′多包含1个L2-型交错圈,与A′包含L2-型交错圈个数的最大可能性矛盾.
注意到Ln中任意两个M-交错面圈都是相容的,而且任意一个M-交错面圈都与任何一个L2-型交错圈相容.根据推论2.4和2.5,可推出下面的结果.
推论2.6设M是线性亚苯基系统Ln的一个完美匹配,则M的反强迫数等于Ln中所有M-交错面圈和L2-型交错圈总个数.
§3 线性亚苯基系统的强迫多项式
定理3.1线性亚苯基系统Ln的强迫多项式满足递推关系


根据推论2.1和定理3.3,可推出下面反映自由度渐近行为的结论.
推论3.2设Ln是含有n个苯环的线性亚苯基系统,则
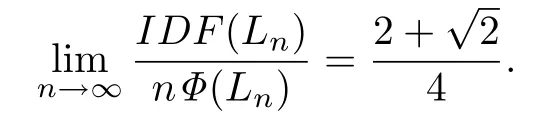
§4 线性亚苯基系统的反强迫多项式
定理4.1线性亚苯基系统Ln的反强迫多项式满足递推关系



根据推论2.1和定理4.3,可得到下面关于反自由度渐近行为的结果.
推论4.2设Ln是含有n个苯环的线性亚苯基系统,则

根据定理3.3和定理4.3,可得到下面反自由度对于自由度的渐近行为.
推论4.3设Ln是含有n个苯环的线性亚苯基系统,则

