时域半平面裂缝反演问题的线性抽样法求解

秦艺濛 ,陈 博 ,岳 洋

(1.中国民航大学 理学院,天津 300300;2.吉林化工学院 理学院,吉林吉林 132022)

§1 引言

声学正反散射问题是一类重要的数学物理问题,正散射问题通常求解散射体对声波散射形成的散射场,反散射问题则通过入射场和已知散射场数据反演散射体的位置和形状[1-2].通常,将声学正反散射问题分为两类: 频域问题和时域问题.频域问题关心的声波是时谐的,从而可以忽略时间变量的影响,最终对Helmholtz方程进行分析和求解.时域问题则关心时间相关的波动问题,其理论分析较为复杂,时间变量的存在也增加了问题数值求解的复杂度.受此影响,虽然频域问题的研究已较为完善,时域研究中却还有很多关键问题未得到解决.

虽然时域问题的研究较为困难,但其问题描述更接近实际问题,更利于直观了解物理过程,并且时间相关的多频数据包含更加丰富的信息,更容易取得较好的反演效果,因此,时域问题近年来受到越来越多的关注[3-4].

本文关心时域半平面裂缝反演问题的求解,其所对应频域问题的研究已较为充分,研究者已经使用Newton迭代法,因子分解法和线性抽样法等方法求解此问题[5-7].相反的,时域裂缝反演问题的研究寥寥无几,文献[8]使用线性抽样法对二维自由空间中裂缝反演问题进行求解,而对于半平面内的裂缝反演问题,由于其涉及半平面边界对声波的散射,散射体具有无界特性,不能直接进行求解.因此,先使用对称延拓[9]的方法将此问题转化为自由空间中有界散射体的对称散射问题.然后,对于反散射问题,使用线性抽样法进行求解,并借助半空间内Green函数对半空间问题线性抽样法的“爆破性”进行证明.

§2对正散射问题进行分析,利用对称延拓的手段将原半平面问题转化为全平面内对称散射问题,并证明该对称散射问题与原问题等价;§3给出反散射问题求解的线性抽样法,并给出半空间问题“爆破性”的证明;§4给出几个数值算例,证明本文算法的有效性.

§2 正散射问题

考虑在声软无界水平基底上有均匀的可穿透介质,介质内部有在某方向l上无穷延伸的裂缝,使用平行l方向的线源发射的柱面波作为入射波,在垂直l的横截面上进行分析,建立正反散射问题模型,即得到二维半平面散射问题.

在二维空间中,采用Cartesian坐标(x1,x2),半平面问题如图1所示.记上半平面和下半平面分别为={x=(x1,x2) :x2>0}和={x=(x1,x2) :x2<0},半平面的边界为={x=(x1,x2) :x2=0},裂缝由二维空间中为无尖点的,自身不相交的分段光滑有向曲线Γ表示.将有向曲线Γ对应前进方向的左侧定义为曲线的左侧,记为Γ−,同理定义曲线的右侧Γ+,波场在和Γ上满足Dirichlet边界条件.

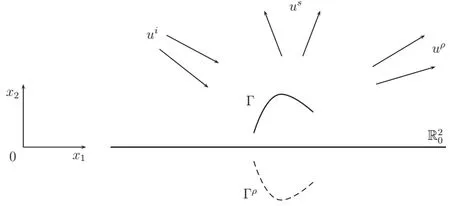
图1 半平面内裂缝散射问题示意图

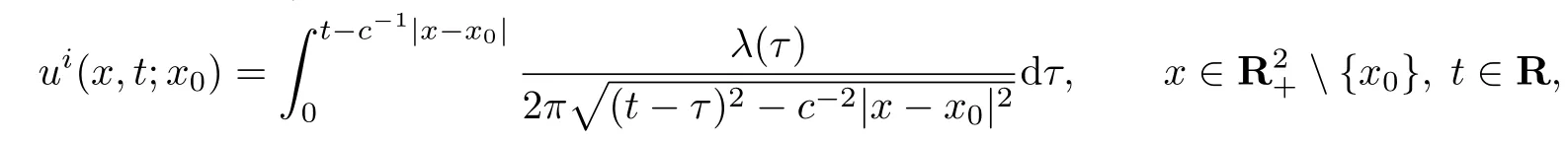
其中x0为源在二维截面中的位置,c为声波在均匀介质中的传播速度,λ(t)为满足因果性的信号函数.这里,λ(t)满足因果性是指当t<0时,λ(t)=0.

考虑全空间R2内D’Alembert算子c−2∂tt −∆的Green函数

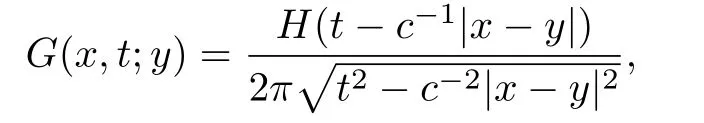
其中H为Heaviside函数,∂tt=∂2/∂t2.则入射场恰为Green函数和信号函数的卷积,即

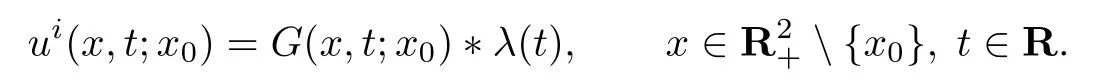
对二维空间内一点x=(x1,x2),定义xρ=(x1,−x2)为其关于x1轴的对称点.由于半平面问题的特殊结构,将声波总场utot分解为入射场ui,反射场

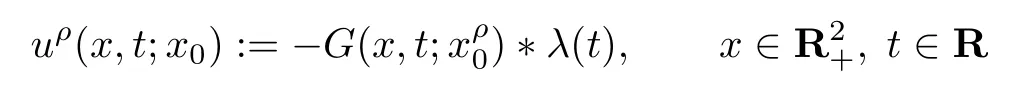
和散射场u三个部分.

散射场u=utot −ui −uρ满足

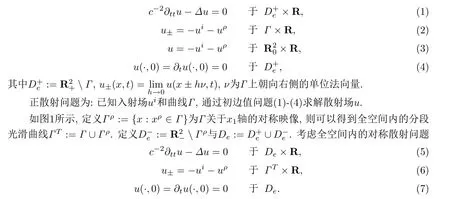
下面命题表明,对称散射问题(5)-(7)和半空间内的原散射问题(1)-(4)等价.

命题2.1散射问题(1)-(4)与(5)-(7)等价.也就是说,若uh(x,t),x ∈D+e,t ∈R为问题(1)-(4)的解,则

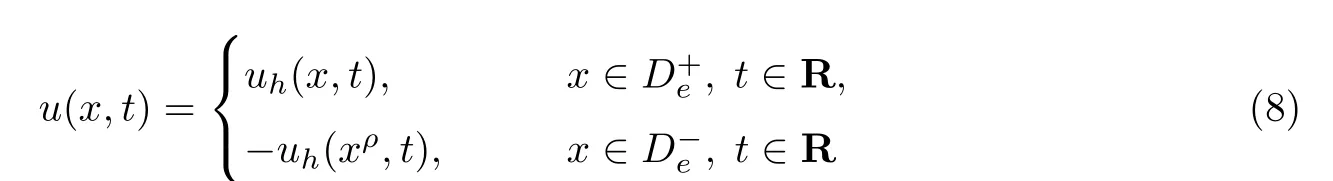
为问题(5)-(7)的解.反之,若u(x,t),x ∈De,t ∈R为问题(5)-(7)的解,则uh=为问题(1)-(4)的解.

证若uh(x,t),,t ∈R为问题(1)-(4)的解,对uh做奇延拓可得由(8)式定义的u.由ui和uρ的定义可知,ui+uρ关于变量x1为奇函数,则对问题(1)-(4)做奇延拓即得问题(5)-(7).由对称延拓的性质可知,u为问题(5)-(7)的解.

若u(x,t),x ∈De,t ∈R为问题(5)-(7)的解,则由u满足(5),(6)及(7)分别可以得出uh=满足(1),(2)及(4).

此外,由文献[8]命题1可知,问题(5)-(7)有唯一解,则问题(5)-(7)的解u(x,t)必关于x1为奇函数.若不然,定义

若u(x,t)不关于x1轴对称,则w1/=w2.又由问题(5)-(7)的对称性,w1和w2均为问题(5)-(7)的解,这与问题解的唯一性矛盾,则u(x,t)关于x1为奇函数.则有u=0于×R,则uh满足方程(3).综上所述,uh为问题(1)-(4)的解.

这样,得到了一个与半空间问题等价的对称散射问题,求解半空间问题时,只需要对全空间内对称问题求解即可.对称散射问题的求解和经典裂缝散射问题一致,使用推迟势边界积分方程方法[8]进行求解,这里不做具体的描述.

§3 反散射问题

先简单介绍一些广义函数空间理论(详见[4,9-10]),引入Fourier-Laplace变换

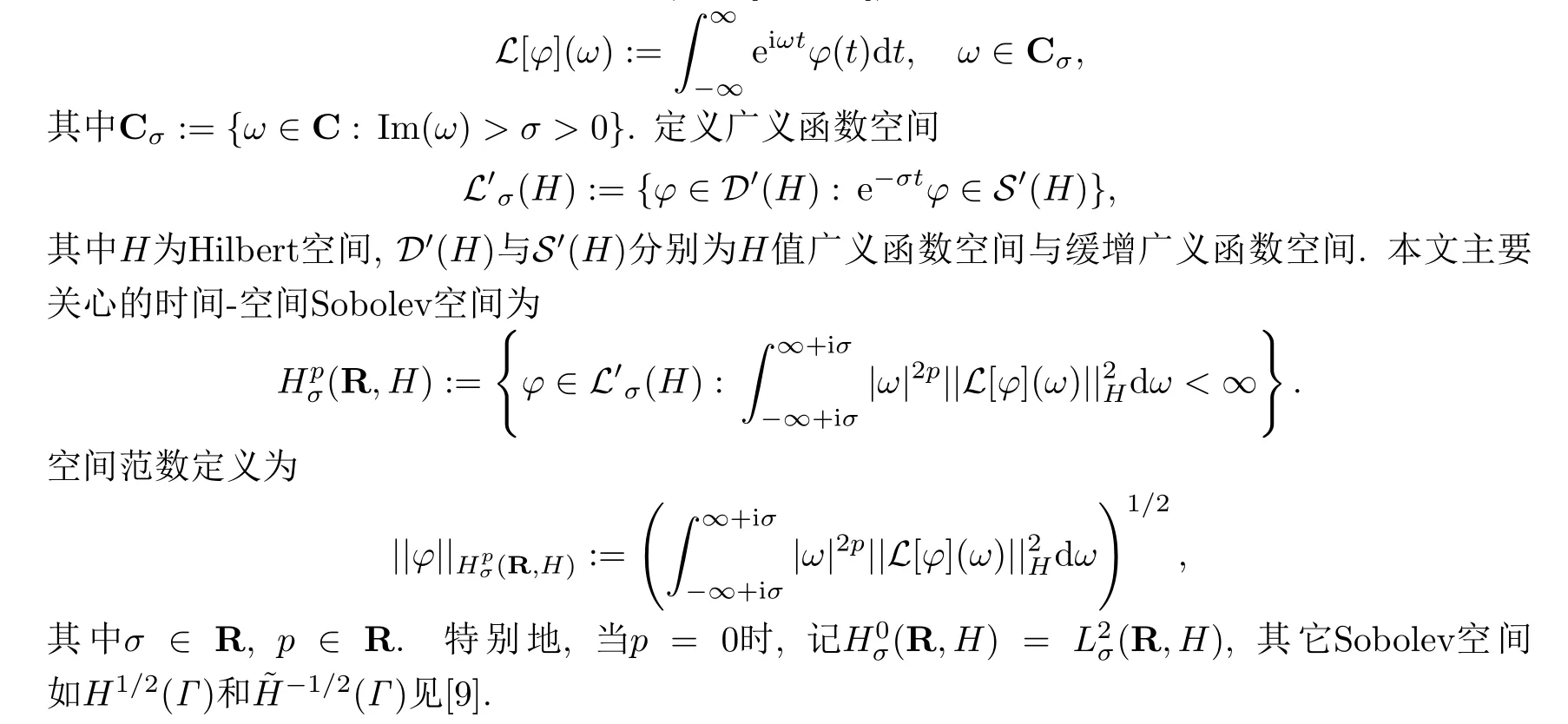
为描述反问题,首先需要定义入射曲线Γi和测量曲线Γm,本文中,两者均取为两端在上的半圆形弧段,且假设两者与所围成的封闭区域均包含裂缝区域Γ.在数值实验中,通常选取Γi=Γm.

本文关心的反散射问题为: 已知入射场ui和探测数据

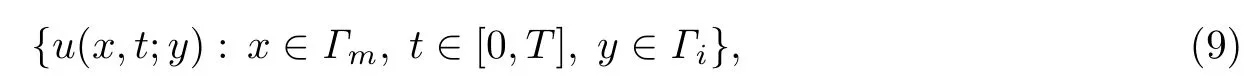
结合初边值问题(1)-(4)反演曲线Γ的位置和形状.

为了探究半空间散射问题的特征,直接对半空间内散射问题(1)-(4)进行分析.半空间问题中的散射场为u=utot −ui −uρ,这与一般散射问题的散射场定义不同,求解分析也会有差异.因此,需要定义半空间内新的的单层位势函数

为有Dirichlet边值半空间内D’Alembert算子的Green函数.由上文对入射场和反射场的分析可知

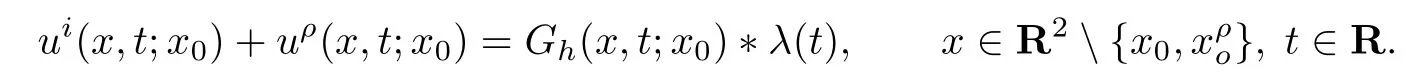
这表明半空间Green函数直接蕴含了对称散射问题的对称特征,因此,使用半空间Green函数对对称散射问题进行求解更为方便.

接下来,考虑反散射问题的线性抽样法求解.首先,定义半空间问题的近场算子

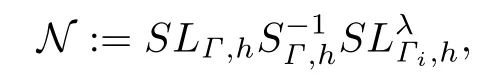
对于半空间问题,还需要定义有对称性质的检验函数[9]

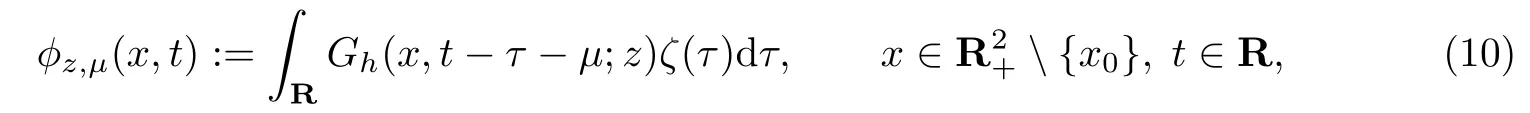
其中µ∈R为时移参数,ζ(t)为有紧支集的光滑函数,为抽样点.

则线性抽样法为: 选取时移参数µ和抽样点z,求解近场方程

得gz,µ.经典的“爆破性”理论表明,‖gz,µ‖在裂缝区域和裂缝之外区域的取值有明显不同,在此基础上可以描绘‖gz,µ‖−1的图像近似反演裂缝位置.

对于全空间裂缝反演问题时域线性抽样法的“爆破性”,[8]中给出了具体的证明.然而,本文描述的问题具有对称性质,相应的近场算子和检验函数定义也与[8]中不同.并且,根据半空间障碍散射问题的研究经验,‖gz,µ‖不单单在散射体内外表现不同,在半空间边界上也有特殊性质.因此,接下来对半空间线性抽样法的“爆破性”做简单证明.

对于裂缝反演问题的分析,通常需要一个新的检验函数ϕL,µ.为适应对称问题的特征,本文定义的ϕL,µ仍然需要具有对称性.下面命题给出ϕL,µ的定义和一个关键性质.

注半空间问题线性抽样法在数值计算时无法区分散射体边界和半空间边界,这一问题在其它半空间问题中也都存在,命题3.1较为直观地诠释了半空间裂缝反演问题线性抽样法的这一本质特征.

尽管命题3.1结论与[8]中经典检验函数的性质不同,类似[8]中的证明方法,仍然能够得到如下的“爆破性”结果,这里不再重复具体的证明.

定理3.2设σ >0,p ∈R,µ∈R,Γ和L为无尖点的,自身不相交的分段光滑曲线.则

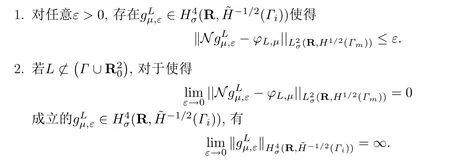
注意到本文开始定义的近场方程(11)使用了检验函数ϕz,µ,而“爆破性”的证明却是对检验函数ϕL,µ进行的.然而,当选取适当的密度函数ζ(x,t)时,检验函数中的曲线L可以退化成一点z,这保证了使用近场方程(11)进行求解的可行性.

§4 数值实验

本节中,给出几个数值算例验证线性抽样法对时域半平面裂缝重构的可行性.选取信号函数为,波速c=1,时滞参数µ=10,取结束时间T=20,时间步数NT=129,时间离散为tn=nκ,n=0,1,···,NT −1,κ=T/(NT −1).选取抽样区域为矩形区域[−3,3]×[0,3],抽样点为抽样区域内的61×31个均匀网格节点.

测量数据(9)使用推迟势边界积分方程方法通过数值模拟得到,其中发射点和测量点均取为4,k=1,2,···,7.在反演时,使用添加了随机噪声的数据

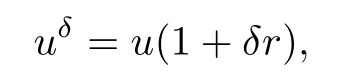
其中δ为噪声水平,r为取值在[−1,1]上的随机数.

在第一个试验中,分别对半平面内的裂缝

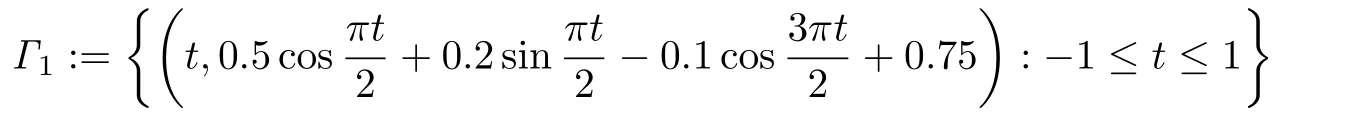
和

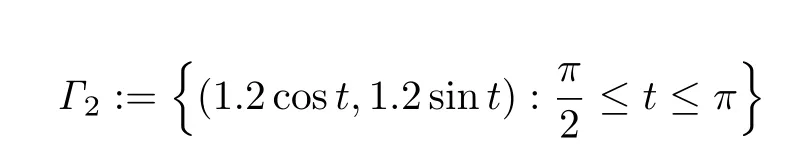
进行反演,噪声水平选取为δ=1%和δ=5%两种情形.实验结果如图2所示,由图2可以看出,不论裂缝是否与半平面边界相交,本文算法对裂缝都有较好的反演效果.从反演效果中,也能看到半平面问题数值计算的特征,即在半平面的边界处图像会有一定的扰动,这是由于半空间Dirichelt边界的存在造成的,这也与命题3.1和定理3.2的结论一致.

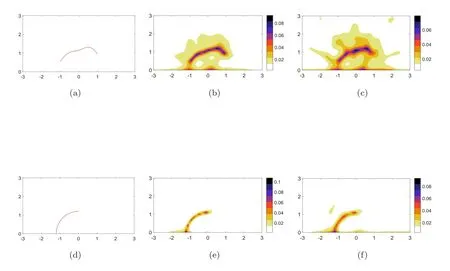
图2 对半空间内单个裂缝的反演 (a)Γ1的真实形状 (b) 对Γ1的反演, δ=1% (c) 对Γ1的反演, δ=5% (d)Γ2的真实形状 (e) 对Γ2的反演, δ=1% (f) 对Γ2的反演, δ=5%

在第二个实验中,考虑使用线性抽样法对多个裂缝的反演.选取裂缝为一个L型裂缝和一个圆弧形裂缝的组合,其中L型裂缝为连接(0.5,2),(0.5,1)和(1,1)三点的折线段,圆弧形裂缝为

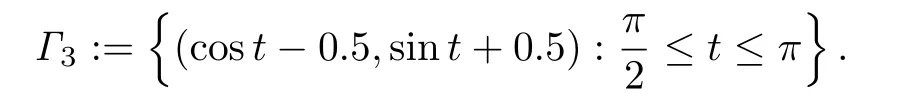
实验结果如图3所示,可以看出,在噪声较小时,反演算法对多个裂缝的反演是有效果的.

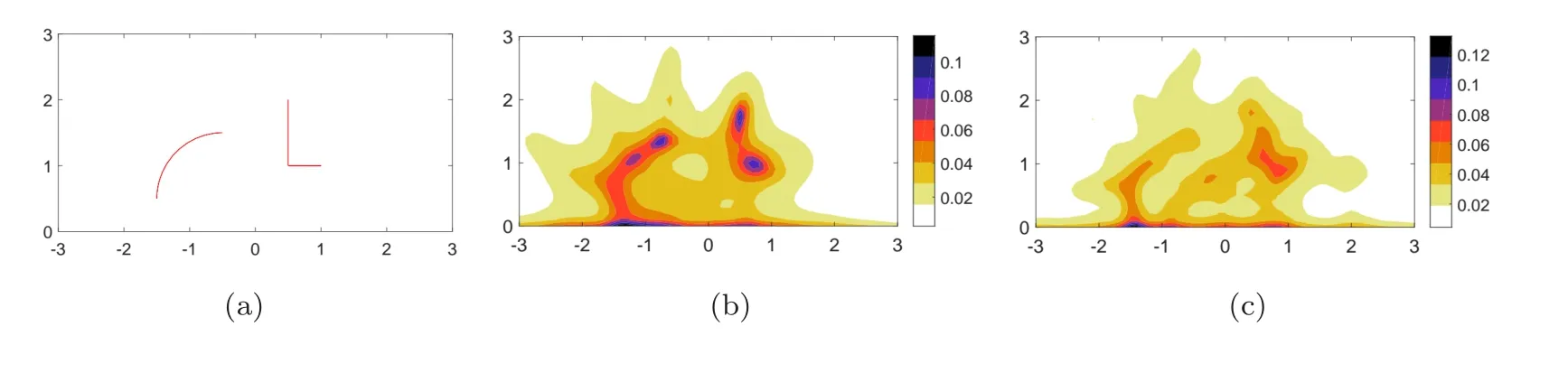
图3 对半空间内多个裂缝的反演 (a) 多个裂缝的真实形状 (b) 对多个裂缝的反演, δ=1% (c) 对多个裂缝的反演, δ=5%