光滑水平面内弹簧振子运动的周期性问题
2023-01-02陈丽娟鲁世平
陈丽娟,鲁世平
(南京信息工程大学 数学与统计学院,江苏南京 210044)
§1 引言
周期问题是常微分方程理论中一类特殊的问题,它与自然界中广泛存在的周期现象息息相关.生物工程和天体力学中许多周期现象都可以转化成周期边值问题来刻画,因此在常微分方程定性理论的研究中周期性的研究具有重要意义,特别是带有奇性的微分方程周期解的存在性问题,由于其物理学上的背景,受到越来越多学者们的关注,弹簧振子在水平面内的运动微分方程就是其中之一.
弹簧振子是由一端固定在平面上不动的轻质弹簧和栓连在其另一端的小球所构成,受稳定约束的弹簧振子在水平面上的运动是工程学中一种非常重要的非线性运动,其动力学模型是理论力学中不可积系统的典型模型.对于弹簧振子单自由度运动,文[1]对于一维振动问题给出了详细的介绍,振动方程具有三角函数形式的解析解,运动规律和物理图象也非常清晰.而一般单自由度系统难以描述运动过程中的实际情况,因此需要用两个坐标的双自由度系统来描述.在弹簧振子双自由度动力学问题中,文[2-6]将弹簧振子的运动看作振动与匀速圆周运动相结合的双自由度系统,文献[2]在直角坐标系下,利用计算机模拟研究了弹簧振子的运动,而文[3]利用摄动法得到振子运动的极坐标方程的一个级数解,但都由于方程形式复杂,难以得出一般性规律.
一般弹簧振子双自由度运动,由于振子的运动方程和速度方程是具有强奇性的非线性方程,难以寻求具体的解析解,讨论其运动规律相当困难,目前关于该模型的动力学研究并不多见.本文运用重合度理论,首先探讨了具有强奇性的弹簧振子径向的运动微分方程周期正解的存在性,然后通过径向和横向运动之间的联系,得到弹簧振子横向运动的周期性.文[7-10]曾利用重合度拓展理论研究了一系列非线性模式的周期解问题.
§2 运动微分方程的建立
一端固定的弹簧振子在光滑水平面上运动,定义径向为弹簧伸缩的方向,横向为水平面内垂直于径向的方向.设弹簧的弹性系数为k,原长为l0,t时刻弹簧的长度为ρ(t),与初始时刻方向的夹角为θ(t).ρ0表示初始时刻的弹簧长度,拴在弹簧另一端的小球质量令为m,在释放弹簧振子的同时,给小球一个横向速度,则小球获得初角速度ω0在光滑平面上运动.
不妨设小球沿逆时针方向运动,t时刻点P处的极坐标为(ρ(t),θ(t)),令径向的基本单位向量为eρ,横向的基本单位向量为eθ,则点的径矢为r(t)=ρ(t)eρ.由于弹簧振子在光滑水平面上运动,没有重力加速度[11],因而加速度为

又由小球只受径向力−k(ρ −l0)eρ作用,从而可得

令ρ=u1,ρ′=u2,θ=u3,θ′=u4,则(1)转化为

由(2)的第2,4两式可得
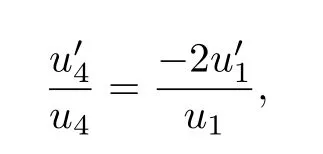
又θ′(0)=u4(0)=ω0,从而解得

再将(3)代入(2)的第2式,得

由此可见(4)即为弹簧振子的径向运动方程,(3)是径向和横向之间的运动关系式.然而由于(4)是具有强奇性的非线性微分方程,求解相当困难,因此下面借助于Mawhin重合度理论和数学分析的技巧,探讨(4)周期正解的存在性.
§3 运动微分方程的周期正解
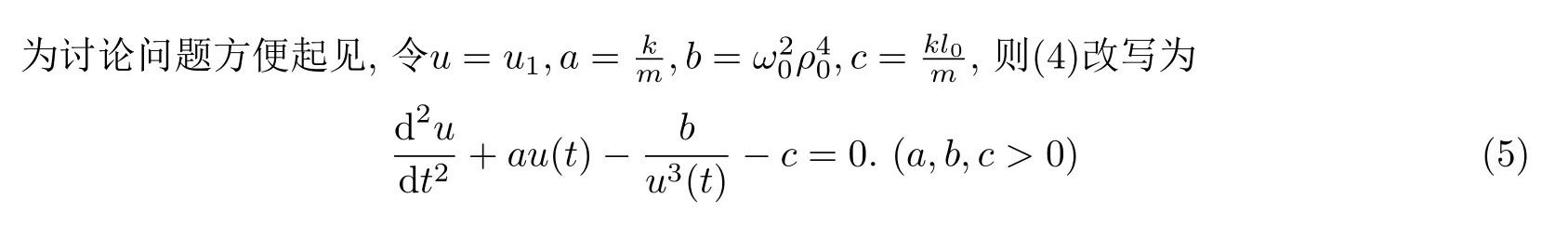
现考虑(5)的T-周期正解存在性问题.

易见方程(5)可转换成算子方程Lu=Nu.此外根据算子的定义,不难得出L的核空间和像空间分别为

因此L-是指标为零的Fredholm算子.
令投影算子P,Q分别为

根据积分中值定理,存在ξ ∈[0,π],使



从而引理1中的3)成立.因此由引理1,(5)存在T-周期正解.
§4 模型条件的可行性
1) 对于弹簧振子径向运动方程的周期解的存在性而言,模型中的系数a满足条件2aT2<1,即a <,说明a是比较小的正数.这与文[11]中取刚度小,韧性高的弹簧所作的假设(k=0.1,m=1,a==0.1)相符合,同时利用MATLAB数值模拟振子的运动轨迹,通过相图验证某一初值对应下的弹簧振子的运动轨迹为圆的结论相符合.
2) 模型中的系数b和c并不是实质性的参数,它们的取值不能决定方程周期正解的存在性,但会影响周期的大小以及精确程度.这与文[2]和[13]借助计算机模拟的质点球在相应的坐标随时间演化的曲线图中可以看出,在不同的弹簧初始长度和加速度的情况下,小球在x和y方向的振幅随时间不停的变化,但整体呈现出周期性的结论相一致.
§5 结论
1) 由(5)存在T-周期正解,得到弹簧振子的径向运动具有周期性的特点,再通过径向和横向之间的运动关系式(3),从而可以得到弹簧振子的横向运动也具有周期性的规律,整体呈现出周期性运动的规律.
2) 方程(5)在一般情况下,无论是求解析解还是用数值计算的模拟解都比较困难.由于方程具有强奇性,而奇性有助于微分方程周期解的形成.对于强奇性,原点附近的能量趋于无穷大,这样的特征对运用度理论来估计先验界相当有利.因此,在周期解存在性的证明过程中奇性条件非常重要,这使得具有奇性的微分方程的研究受到更广泛的关注.尽管非线性微分方程理论日趋成熟,但是奇性方程由于其复杂性,仍然具有很大的研究价值.
3) 本文研究的弹簧振子在光滑水平面内运动,是弹簧振子运动的一种特殊形式,因为没有重力加速度,从而降低了非线性程度.如果考虑重力加速度,在水平面内运动的弹簧振子,由于重力加速度的存在,非线性程度明显增强,那么是否也存在周期性的运动规律? 因此在本文研究的基础上,还可以探讨一般情形下弹簧振子运动的动力学行为.
