Banach空间中广义混合拟变分不等式解的存在性

郑琼悦,林惠玲

(福建师范大学数学与统计学院,福建福州 350117)

§1 引言

变分不等式最早由Hartman-Stampacchi[1]于1966年首次提出,随后众多学者对其进行研究并推广,目前的研究成果主要集中在拟变分不等式[2-3],广义变分不等式[4-5],以及混合变分不等式[6-7].同时,变分不等式及其推广形式被广泛应用于经济均衡,控制论,对策论,金融,交通,工程科学等领域.

设B为Banach空间,B∗为其对偶空间,K:B →2B为集值映射,F:B →为集值映射,f:B →R∪{+∞}为真凸下半连续泛函.本文考虑如下广义混合拟变分不等式问题(简记为(GMQVI(K,F,f)),即找到x ∈K(x),v ∈F(x),使得

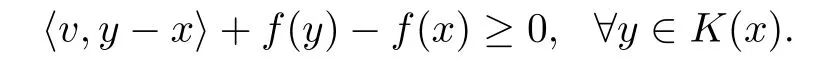
下面介绍GMQVI(K,F,f)的一些特殊形式.

若C是B中的非空闭凸集,K(·)≡C,则GMQVI(K,F,f)就退化为广义混合变分不等式(记为GMVI(C,F,f)[4]),即找到x ∈C,使得

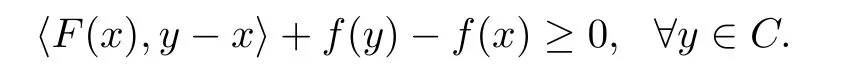
若∀x ∈B,f(x)=0,则GMQVI(K,F,f)就退化为广义拟变分不等式(记为GQVI(K,F))[8],即找到x ∈K(x),v ∈F(x),使得

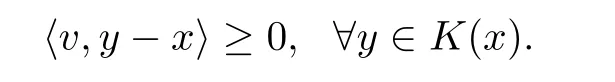
若∀x ∈B,f(x)=0,C是B中的非空闭凸集,K(·)≡C,F为单值映射,则GMQVI(K,F,f)就退化为经典变分不等式(记为VI(C,F)[1]),即找到x ∈C,使得

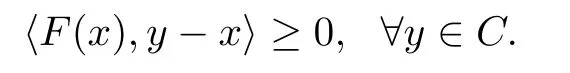
当C=K为闭凸锥时,变分不等式问题就变为互补问题,因此变分不等式问题和互补问题有着密切联系,很多学者对两者解的存在性都进行了研究,见文献[9-12].变分不等式的研究方法有很多,例如凭借KKM原理以及变分方法[13],Browder不动点定理,拓扑度理论[14-16],或极小极大理论,或是构造强制性条件以及例外簇[17-18]等,其中引入例外簇来研究变分不等式及其推广形式是一种新颖且应用广泛的方法.

1984年,Smith[19]首次提出例外簇和例外序列的概念,并将其应用于单值的互补问题解的存在性研究中.随后很多学者也逐渐用例外簇来研究VI(K,F)的解的存在性.例如Isac[18]在闭凸锥上定义集值映射的例外簇,用Leray-Schauder择一定理代替拓扑度,证明了在Hiblert空间中互补问题要么存在例外簇,要么有解.由于互补问题与变分不等式有密切联系,Zhou[20]等人通过定义新的例外簇,将此方法推广到了无限维Hilbert空间,并得到变分不等式不存在例外簇则必定有解.2005年,Li和Whitaker[21]在Banach空间的闭凸锥上给出完全连续场例外簇的概念,并定义广义的(θ)条件,从而得到变分不等式或者有解或者完全连续场关于闭凸锥有例外簇.2010年,刘智[22]等人通过引入新的例外簇,在集值映射具有紧收缩值的条件下,研究Banach空间中广义变分不等式解的存在性,将文献[23]应用于单值映射的结果推广到集值映射.因此,通过引入例外簇概念,利用拓扑度或Leray-Schauder择一定理,得到解的存在性与例外簇的关系,并探究强制性条件来确保解的存在性的研究方法已受到国内外许多学者的关注.

对于GMQVI问题,除了Wang等人[16]通过在有限维空间建立度理论来研究GMQVI解的存在性外,极少有文献对Banach空间的GMQVI问题进行研究.甚至据作者所知,当K为集值映射时,尚未有文献利用例外簇来研究该问题.受以上文献的启发,本文将在自反的Banach空间中,在一定条件下,证明当GMQVI的可行集S为有界集时,GMQVI 有解;当S为无界集时,提出新的例外簇概念,并通过Leray-Schauder择一定理证明广义混合拟变分不等式不存在例外簇,则必定有解.最后,分析不存在例外簇的充分条件,各充分条件间的关系并且得到GMQVI 解存在的必要性.

本文用到如下符号.

“→”和“⇀”分别表示序列的强收敛与弱收敛.C ⊂B表示B中的非空子集,A ⊆C表示集合C包含集合A.intC,分别表示C的内部,边界,闭包.B(x,r)和(x,r)分别表示B中以x为中心,r为半径的开球和闭球,用Graph(F)={(x,y)∈B ×B∗,x ∈B,y ∈F(x)}表示映射F的图像.记S={x ∈B:x ∈K(x)}为广义混合拟变分不等式GMQVI(K,F,f)的可行集,它也是K的所有不动点集合.任意的x,x′ ∈B,则K(x)在x′的广义f-正规锥定义为

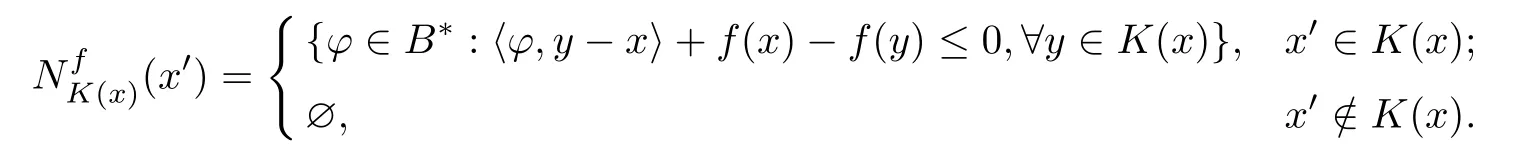
§2 预备知识

本节介绍本文所需要的一些基本概念及其性质,并探讨GMQVI(K,F,f)解的等价刻画.下面介绍集值映射的相关概念.

定义2.1(见[2,24]) 设X,Y为Banach空间,F:X →2Y为非空集值映射,泛函f:X →R∪{+∞}.

(1) 若对Y中任意包含F(x)的开集W,存在X中包含x的一个开邻域U,使得F(U)⊆W,则称F为在x ∈X处的上半连续映射.若F在每一点x ∈X处为上半连续映射,则称F为X上的上半连续映射.

(2) 若Graph(F)为X ×Y上的凸集,则称F为凸图像映射.

(3) 若对任意一个有界子集A ⊂X,F(A)为Y中的相对紧集,则称F为紧映射.

(4) 若C ⊂X为非空子集,∀(x,v),(y,w)∈Graph(F),有

则称F在C上是f-伪单调.

除非特殊说明,在本文中总假设集值映射K:B →2B为B上的凸图像及连续映射,可行集S为非空集,则类似文献[8]中定理2.1.1证明可知,可行集S是非空闭凸集.下面介绍正规对偶映射及其性质.

定义2.2正规对偶映射J:B →,定义为

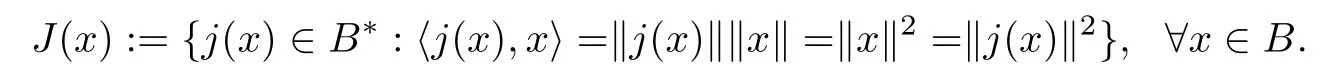
其中‖x‖和‖j(x)‖分别表示Banach空间B及其对偶空间B∗中的范数.

正规对偶映射[25-26]具有较为丰富的性质,下面列举几个本文所需的性质.

(1) 任意Banach空间中,J为单调有界的.

(2)B为自反Banach空间,则对任意x ∈B,J(x)为非空有界闭凸的,且J(αx)=αJ(x).

(3)B为光滑的Banach空间,则J:B →B∗为单值,连续映射.

(4)B为自反光滑,严格凸的Banach空间,J∗:B∗→B为B∗上的正规对偶映射,则J−1=J∗,JJ∗=IB∗,J∗J=IB,其中IB∗,IB分别表示B∗和B上的单位映射.

Wu和Huang[26]定义了如下泛函V(ϕ,x):B∗×B →R∪{+∞},

其中ρ>0,ϕ ∈B∗,x ∈B,f:B →R∪{+∞}为下半连续的真凸泛函.

广义f-投影算子具有如下特殊形式.

(1) 当K(x)≡K ⊂B为非空闭凸集且f(x)≡0时,广义f-投影算子退化成文献[27]中的

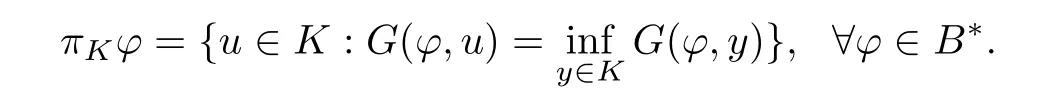
其中对任意的ϕ ∈B∗,x ∈K,G(ϕ,x)=‖x‖2−2〈ϕ,x〉+‖ϕ‖2.

(2) 当B为Rn空间,K为Rn中的非空闭凸集,f(x)≡0,则广义f-投影算子退化成文献[16]中的度量投影算子,定义为

注2.2定理2.1将文献[8]中定理2.2.4的结果从GQVI(K,F)推广到GMQVI(K,F,f)上,并利用广义投影算子的性质简化了文献[8]中的证明.

§3 广义混合拟变分不等式的解的存在性

本节主要利用不动点定理研究广义混合拟变分不等式解的存在性.通过Fan-KKM定理,证明了可行集为有界集时,广义混合拟变分不等式问题存在解;当可行集为无界集时,给出新的例外簇定义,利用Leray-Schauder型不动点定理,证明了GMQVI(K,F,f)不存在例外簇则存在解.

由文献[28]的定理4.2可得,当B为自反Banach空间,有界闭集为弱紧集,结合文献[29]定理3.1,可得下面结论成立.

定理3.1设B为自反光滑严格凸的Banach空间,K:B →2B为取闭凸值的连续凸图像集值映射,F:B →为具有非空紧凸值的(弱拓扑到范数拓扑)上半连续集值映射,S为有界闭凸集,f:B →R∪{+∞}为真凸下半连续泛函满足S ⊆domf,若x ∈B,对任意的y ∈K(x),f在y上连续,则GMQVI(K,F,f)有解.

注3.1定理3.1将[2,30]的结果推广至广义混合拟变分不等式.

当S为无界闭凸集时,引入集值映射的例外簇以及Leray-Schauder择一定理来探究解的存在性.

定义3.1序列{xr}r>0⊂S满足

(i)‖xr‖→∞(r →∞),

(ii)任意的r >0,存在µr >1,vr ∈F(xr),使得则称{xr}r>0为广义混合拟变分不等式GMQVI(K,F,f) 的例外簇.

引理3.1[18](Leray-Schauder 定理) 设U为Banach空间B中的闭子集,0∈int(U),F:U →2B为取非空紧收缩值的紧的上半连续集值映射.若F没有不动点,则满足Leray-Schauder条件:存在(λ∗,x∗)∈(0,1)×∂U,使得x∗∈λ∗F(x∗).

为得到GMQVI(K,F,f)解存在的条件,还需介绍收缩集的定义.

定义3.2设C为Banach空间中任意子集,若对任意x ∈C,存在连续映射h:C×[0,1]→C,使得h(x,0)=x,h(x,1)=x0,其中x0∈C,则称C为可收缩的.

例如,凸集是可收缩的.因为对任意的x0∈C,取映射h(x,λ)=λx0+(1−λ)x,由定义3.2可得C为可收缩的.

下面的结论体现了GMQVI(K,F,f)的解和例外簇之间的密切联系.

定理3.2设B为自反光滑严格凸的Banach空间,满足性质(h),K:B →2B为取闭凸值的连续凸图像集值映射,T=J −F:B →为取非空紧收缩值的紧的上半连续集值映射,其中J:B →正规对偶映射.S为非空无界闭凸集,f:B →R∪{+∞}为下半连续的真凸泛函.任意x ∈B,任意的y ∈K(x),f在y处连续.如果GMQVI(K,F,f)不存在例外簇,则广义混合拟变分不等式GMQVI(K,F,f)有解.

而当r →+∞时,‖xr‖=r →+∞,故广义混合拟变分不等式GMQVI(K,F,f) 存在例外簇,与题设矛盾,故GMQVI(K,F,f)有解.

§4 不存在例外簇的充分性条件

在本节中,讨论当可行集S为无界闭凸集时,GMQVI(K,F,f)不存在例外簇的充分条件,从而得到其存在解的充分条件.此外,当F是f-伪单调的情况下,探讨GMQVI(K,F,f) 存在解的必要条件.

定理4.1B为自反光滑严格凸的Banach空间,K:B →2B为取闭凸值的连续凸图像集值映射,T=J −F:B →取非空紧凸值的紧上半连续集值映射,其中J:B →为正规对偶映射.f:B →R∪{+∞}为真凸下半连续泛函,S为非空无界闭凸集,对任意x ∈B,若对任意的z ∈K(x),f在z处连续,则下列结论有(a1)⇒(a2)⇒(c) 成立.

由定义2.2可知

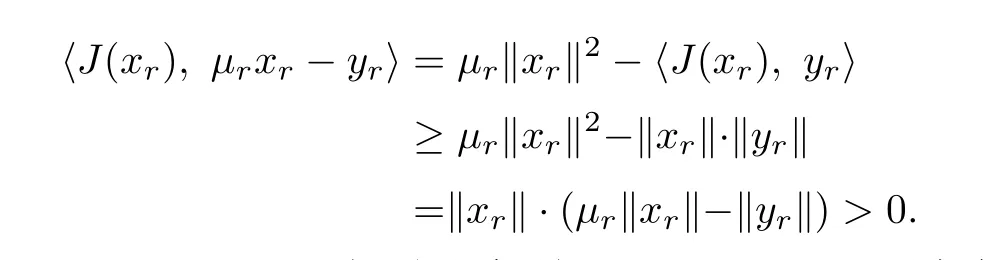
则0≤〈(1−µr)J(xr),µrxr −yr〉<0,得到矛盾,故GMQVI(K,F,f)不存在例外簇.

定理4.2设B为自反光滑严格凸的Banach空间,K:B →2B为取闭凸值的连续凸图像集值映射,T=J −F:B →为取非空紧凸值的紧上半连续集值映射,其中J:B →为正规对偶映射.S为非空无界闭凸集,f:B →R∪{+∞}为真凸下半连续泛函.任意x ∈B,若对任意的y ∈K(x),f在y处连续,则下列结论有(b1)⇒(b2)⇔(b3)⇒(c).

(b1) 对任意的x ∈B,存在y ∈K(x),使得

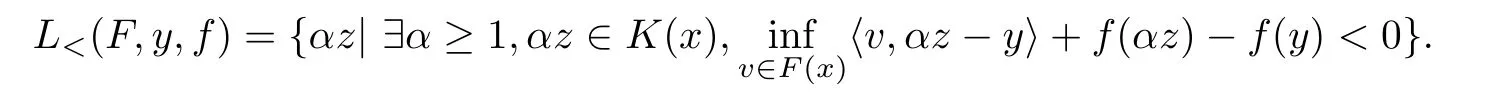
为有界集或空集.

(b2) 对任意的x ∈B,存在K(x)的非空有界子集D,对于任意满足α ≥1,αx ∈K(x)D的(α,x),存在y ∈D使得

类似于定理4.1中(a2)⇒(c)的证明可得,广义混合拟变分不等式GMQVI(K,F,f)不存在例外簇.

注4.1定理4.2 将文[31]中应用于变分不等式的三个相应条件改进并推广到广义混合拟变分不等式GMQVI(K,F,f)上.

以下结论进一步刻画了GMQVI(K,F,f)解集的有界性.

定理4.3设B为自反光滑严格凸的Banach空间,K:B →2B为取闭凸值的连续凸图像集值映射,T=J −F:B →取非空紧凸值的紧的上半连续集值映射,其中J:B →为正规对偶映射.f:B →R∪{+∞}为真凸下半连续泛函,S={x ∈B:x ∈K(x)}为GMQVI(K,F,f)的可行集.当S为非空无界闭凸集时,若对任意x ∈B,任意y ∈K(x),f在y处连续,则下列结论有(c1)⇒(c2)⇔(c3)⇒(d)成立.

(c1) 对任意的x ∈B,存在y ∈K(x),使得

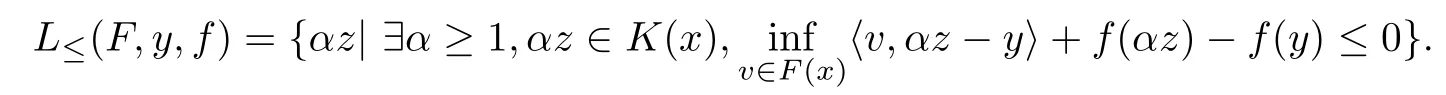
为有界集.

(c2) 对任意的x ∈B,存在K(x)的非空有界子集D,使得任意满足α ≥1,αx ∈K(x)D的(α,x),存在y ∈D使得

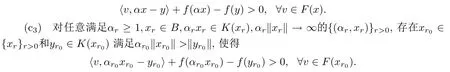
(d) 广义混合拟变分不等式GMQVI(K,F,f)解集非空有界.

证类似于定理4.2中(b1)⇒(b2)⇔(b3) 的证明,可证(c1)⇒(c2)⇔(c3).

(c3)⇒(d): 由定理4.2中(b3)⇒(c),可得GMQVI(K,F,f)不存在例外簇,结合定理3.2,可得GMQVI(K,F,f)解集非空.

下证有界性,用反证法.若{xr} ⊂S为GMQVI(K,F,f)的无界解集,满足‖xr‖ →+∞(r →∞),由xr为GMQVI(K,F,f)的解,则存在vr ∈F(xr),使得

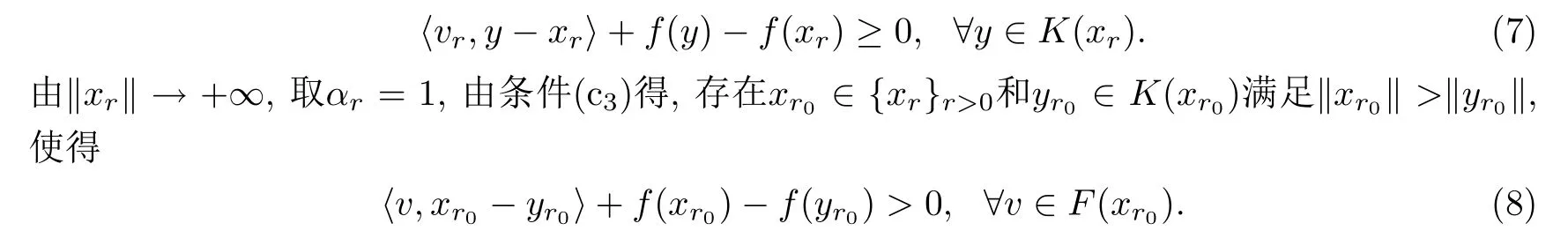
取式(7)中xr==,取式(8)中v=vr,则相应的(7)和(8)矛盾,故广义混合拟变分不等式GMQVI(K,F,f)解集非空有界.

在F是f-伪单调的条件下,得到如下关于GMQVI(K,F,f)解存在的必要性.

定理4.4设B为自反光滑严格凸的Banach空间,K:B →2B为取闭凸值的连续凸图像集值映射,T=J −F:B →取非空紧凸值的紧上半连续集值映射,其中J:B →正规对偶映射,f:B →R∪{+∞}为真凸下半连续泛函.S={x ∈B:x ∈K(x)}为GMQVI可行集,S为非空无界闭凸集.若对任意x ∈B,任意的y ∈K(x),f在y处连续,则下列结论有(i)⇒(ii)⇒(iii)成立.