非负矩阵最大特征值的上下界估计

钟 琴,赵春燕 ,王 妍 ,牟谷芳

(1.四川大学锦江学院 数学教学部,四川眉山 620860;2.成都信息工程大学 应用数学学院,四川成都 610225)

§1 引言

非负矩阵是一类重要的矩阵,在矩阵理论研究领域具有广泛的应用.非负矩阵具有很多优美的性质,国内外的学者对非负矩阵的最大特征值和Perron向量进行了广泛而深入地研究，取得了很多优秀的成果[1-12].矩阵理论专家Frobenius和Perron卓有建树的工作使得非负矩阵理论得以迅速发展,其中著名的Perron-Frobenius定理在理论和实际工作中常被用到.估计非负矩阵最大特征值的范围是非负矩阵理论研究的热门课题.

用A ≥0(aij ≥0)表示矩阵A为非负矩阵,A>0(aij >0) 表示矩阵A为正矩阵.记ρ(A)=,i ∈〈n〉},其中λi为非负矩阵A的n个特征值,则由Perron-Frobenius定理[1]知ρ(A) 为非负矩阵A的一个特征值，称为非负矩阵A的最大特征值.

设矩阵A=(aij)n×n,如果存在一个排列方阵P使得P APT=其中A11和A22是两个低阶方阵,则称A是可分的(或可约的);否则称A是不可分的(或不可约的).

若A是非负不可约矩阵,则存在正向量u,v,使得Au=ρ(A)u,vTA=ρ(A)vT,称u为A的右Perron特征向量,v为A的左Perron特征向量.

对列和结论同样成立.

对于正矩阵,Lederman[2],Ostrowski[3]和Brauer[4]在(1)式的基础上给出了正矩阵最大特征值的界值定理.

对具有非零行和的非负矩阵,Minc[5]对(1)式进行了改进,得到了

文献[6]在矩阵A非负不可约的条件下得到了

这里k为使得ri,i ∈〈n〉的任意正整数,对于列和(3)式结论同样成立.

文献[7]对(3)式进行了如下的改进: 设矩阵A=(aij)n×n ≥0且A具有非零行和与非零列和,则对任意的正整数m,k有

对于列和结论同样成立.

本文将给出非负矩阵最大特征值的一组新界作为对前人研究结果的补充,并且保证这组新界比相关文献中的结果更接近于最大特征值的真实值.

§2 主要结论

引理1[5]设λ是矩阵A的任一特征值,矩阵AT和A对应于λ的特征向量为X=(x1,x2,···,xn)T和Y=(y1,y2,···,yn)T,则

下面给出本文的主要结果.

两边同时取极限得

同理可证对列和的结论也成立.

注1若A0===I,则当k=0,m=1 时,(5)式即为Frobenius界值.

注2在(5)式中令m=1,再根据定理2的证明过程可知

§3 数值算例

例考虑非负矩阵A=

下表给出了文献[1-9]以及定理1对非负矩阵A的最大特征值的上下界估计结果比较.

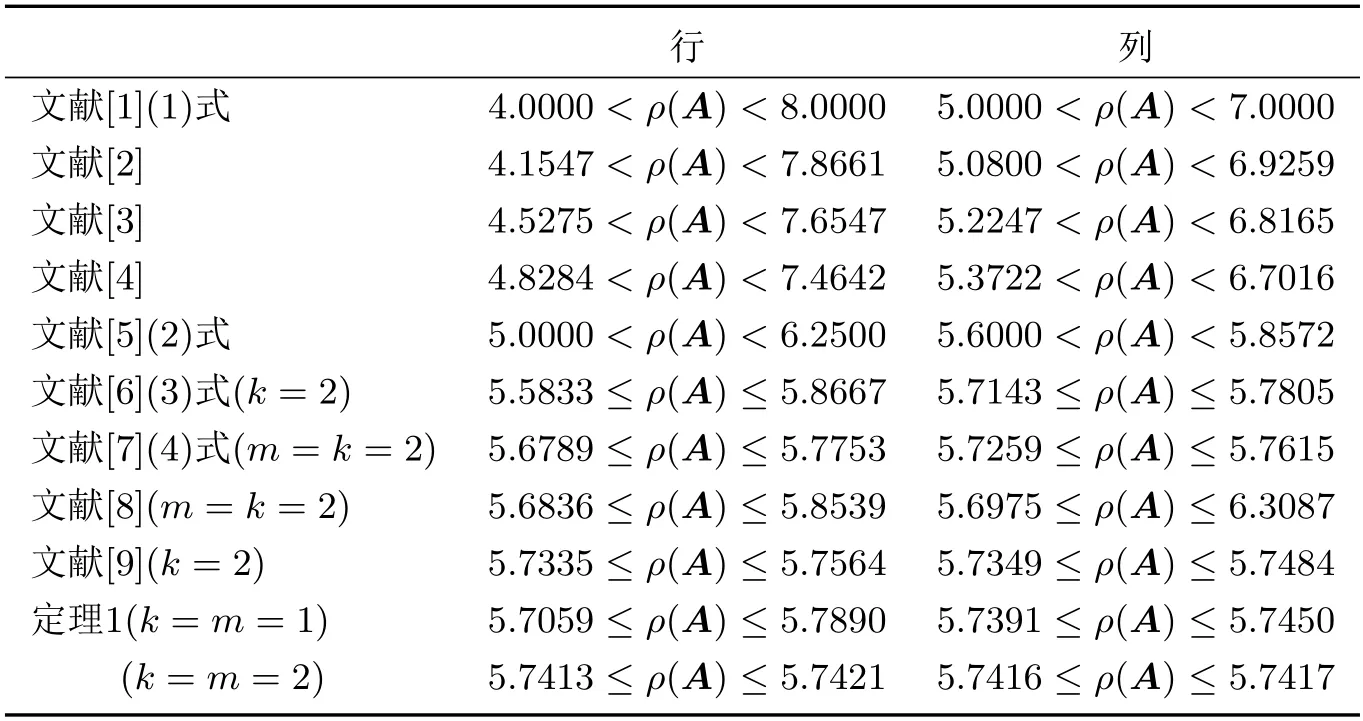
表1 最大特征值的界值比较

实际上ρ(A)=5.74165738···,以上数据表明,定理1得到的结论比现有的相关研究结果更接近真值.

§4 结论

本文通过构造与非负矩阵相关的两个特殊矩阵,给出非负矩阵最大特征值的单调递增的下界估计式和单调递减的上界估计式,并且从理论上证明了上下界估计式的单调性和极限的存在性,最后给出数值算例验证了本文结果的精确性.