Z型三叉树多肽聚苯环系统的Hosoya指标的计算公式
2018-04-28任胜章邓方安霍小莉
任胜章, 申 鹏, 邓方安, 李 坤, 霍小莉
(1. 陕西理工大学 数学与计算机科学学院, 陕西 汉中 723000; 2. 兰州大学 数学与统计科学学院, 甘肃 兰州 730000)
设图G(V,E)是简单的连通无向图,并且V(G)和E(G)分别是它的顶点集和边集.对图G的任意2条边e1和e2,如果他们不相邻,则称他们是相互独立的.一个边集E(G)的子集M,如果他的任意2条边都相互独立,则称他是图G的一个匹配集.用m(G)表示图G的匹配集的个数,在化学中m(G)也被称为Hosoya指标,此指标与化学分子的许多物理和化学性质密切相关,如:分子的熔点、沸点等.图族多肽聚苯环系统图是将相邻苯环被P2路点粘接得到的n个苯环系统的图.称苯环与P2路粘接的条数为苯环的环度.只有一个环度为3的多肽聚苯环系统图称为三叉树多肽聚苯环系统图;没有环度为3的多肽聚苯环系统图称为多肽聚苯链.在三叉树多肽聚苯环系统图中除去环度为1和3的苯环之外,如果苯环被2条P2路粘接的顶点将苯环分割后的顶点集的阶为0和4,称该类三叉树多肽聚苯环系统图为Z型三叉树多肽聚苯环系统图(参见图1),并用Z(k1,k2,k3)表示n(n≥4)个苯环的Z型三叉树多肽聚苯环图,其中k1、k2、k3分别为3个叉上苯环的个数(n=k1+k2+k3+1,n≥4,k1≥1,k2≥1,k3≥1).本文通过对Z型三叉树多肽聚苯环系统图的Hosoya指标进行研究,给出了该类图族的Hosoya指标计算公式,并且刻画出该类图族Hosoya指标取得最值图.在本文中没有给出的术语,记号可参见文献[1].
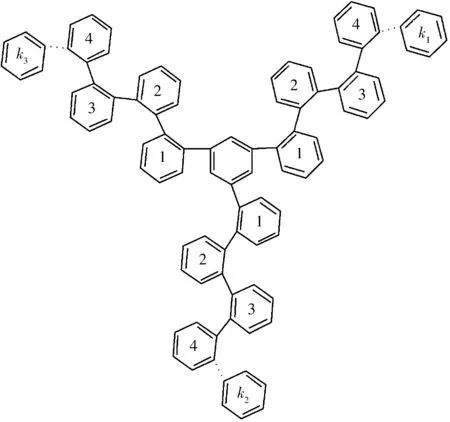
图 1 Z型三叉树多肽聚苯环系统图Z(k1,k2,k3)
1 基本引理
引理1.1[2]设图G1和G2是图G的2个分支且G=G1∪G2,则m(G)=m(G1)m(G2).
引理1.2[2]设图G是简单图且任意的uv∈E(G),则m(G)=m(G-uv)+m(G-u-v).
引理1.3[3]设和并且F(n)和L(n)分别是Fibonacci数列和Lucas数,则:
3) F(m)L(n)=F(n+m)-(-1)mF(n-m)=F(m+n)+(-1)nF(m-n).
引理1.4[4] 设q1,q2,…,qt是递推关系式
H(n)=a1H(n-1)+a2H(n-2)+
…+akH(n-k)
的特征方程的所有互不相等的特征根,并且它们的重数依次为e1,e2,…,et,则递推关系对应于qi部分的解为
Hi(n)=(c1+c2n+…+ceinei-1)qni,
而递推关系式的一般解为
H(n)=H1(n)+H2(n)+…+Ht(n).
引理1.5[4]H(n)=a1H(n-1)+a2H(n-2)+…+akH(n-k)+τ2是非齐次递归关系式,其中a1,a2,…,ak,τ为常数.如果f(n)是其对应的齐次递归关系式H(n)=a1H(n-1)+a2H(n-2)+…+akH(n-k)的通解,那么H(n)=d1f(n)+d2τn是非齐次递归关系式的通解,其中d1、d2是常数.
2 主要结论
没有环度为3的多肽聚苯环系统图称为多肽聚苯链.设z(n)是苯环数为n(n≥3)的Z型多肽聚苯链(参见文献[5]),g(n)、w(n)、t(n)分别由Z型多肽聚苯链z(n)删除最后一个苯环的若干顶点得到的图(参见图2、3),则下面2个引理成立.

图 2 z(n),t(n)

图3 g(n),w(n).
引理2.1[5]设z(n)是苯环数为n(n≥3)的Z型多肽聚苯链,则

引理2.2设g(n)、w(n)、t(n)是苯环数为n(n≥3)的多肽聚苯链,则:
1) m(g(n))=8m(z(n-1))+5m(g(n-1));
2) m(w(n))=3m(z(n-1))+m(g(n-1));
3) m(t(n))=8m(z(n-1))+3m(g(n-1)).
证明由引理1.1和1.2容易证定理结论成立.
定理2.1设g(n)、w(n)、t(n)是苯环数为n(n≥3)的多肽聚苯链,则:
证明结论2)和3)由引理2.1、2.2和定理2.1的1)的结论很容易证明.在这里只给出结论1)的证明,由引理1.1和1.2得到
(1)
由引理2.1,将
,
代入(1)式得到

.
(2)
根据引理1.4可知,常系数齐次递推关系
m(g(n))-5m(g(n-1))=0
的解为5n,那么常系数非齐次递推关系式(2)的解可设为
m(g(n))=c5n+aλn-31+bλn-32.
(3)
将(3)式代入递推关系式(2),解得
(4)
将初始值m(g(4))=87 768,代入上式解得c=0.因此定理2.1的1)的结论成立.
定理2.2设Z(k1,k2,k3)表示n(n≥4)个苯环的Ζ型三叉树多肽聚苯环系统图,则有
m(Z(k1,k2,k3))=
m(z(k2+1))m(z(k1))m(z(k3))+
m(t(k2+1))m(g(k1))m(z(k3))+
m(t(k2+1))m(z(k1))m(g(k3))+
m(w(k2+1))m(g(k1))m(g(k3)).
证明由引理1.1、1.2容易证定理结论成立.
定理2.3设Z(k1,k2,k3)表示n(n≥4)个苯环的Z型三叉树多肽聚苯环系统图,则有
m(Z(k1,k2,k3))=λk1+k2+k3-71×
+
λk1+k2+k3-72+
(λk1+k2-51λk3-22+λk1+k3-51λk2-22+λk2+k3-51λk1-22)+
(λk1+k2-52λk3-21+λk1+k3-52λk2-21+λk2+k3-52λk1-21).
证明令将定理2.1和引理2.1的公式代入定理2.2得到
m(Z(k1,k2,k3))=(a1λk2-11+a2λk2-12)×
(a1λk1-21+a2λk1-22)(a1λk3-21+a2λk3-22)+
(d1λk2-21+d2λk2-22)(b1λk1-31+b2λk1-32)×
(a1λk3-21+a2λk3-22)+(d1λk2-21+d2λk2-22)×
(a1λk1-21+a2λk1-22)(b1λk3-31+b2λk3-32)+
(c1λk2-21+c2λk2-22)(b1λk1-31+b2λk1-32)×
(b1λk3-31+b2λk3-32)=
(a31λ21+2a1b1d1+b21c1λ-11)λk1+k2+k3-71+
(a32λ22+2a2b2d2+b22c2λ-12)λk1+k2+k3-72+
(a21a2λ21+a2b1d1+a1b2d1λ1λ-12+
b1b2c1λ-12)λk1+k2-51λk3-22+(a1a22λ22+a1b2d2+
a2b1d2λ-11λ2+b1b2c2λ-11)λk1+k2-52λk3-21+
(a21a2λ1λ2+2a1b1d2+b21c2λ-11)
λk1+k3-51λk2-22+(a1a22λ1λ2+2a2b2d1+
b22c1λ-12)λk1+k3-52λk2-21+(a21a2λ21+a1b2d1λ1λ-12+
a2b1d1+b1b2c1λ-12)λk2+k3-51λk1-22+(a1a22λ22+
a2b1d2λ-11λ2+a1b2d2+b1b2c2λ-11)λk2+k3-52λk1-21.
将a1、a2、b1、b2、c1、c2、d1、d2的值代入上面等式,并化简得到
m(Z(k1,k2,k3))=λk1+k2+k3-71×
λ
(λk1+k2-51λk3-22+λk1+k3-51λk2-22+λk2+k3-51λk1-22)+
(λk1+k2-52λk3-21+λk1+k3-52λk2-21+λk2+k3-52λk1-21).
因此定理2.3的结论成立.
推论2.1设Z(k1,k2,k3)表示n(n≥4)个苯环的Z型三叉树多肽聚苯环图,则

推论2.2设Z(k1,k2,k3)表示n(n≥4)个苯环的Z型三叉树多肽聚苯环图,则
m(Z(k1,k2,k3))≤m(Z(1,1,n-3)).
3 结束语
在本文中,应用特殊非齐次常系数递推关系式的性质计算出多肽聚苯链w(n)、t(n)的Hosoya指标计算公式,以定理2.1的形式给出.利用以上结果,给出了Z型三叉树多肽聚苯环系统的Hosoya指标的计算公式,以定理2.2和定理2.3的不同形式给出.并刻画出Z型三叉树多肽聚苯环系统的Hosoya指标取得最小值和最大值时的图,以推论2.1和推论2.2的形式给出.
致谢陕西理工大学科研基金(SLGQD14-14和SLGKY15-37)对本文给予了资助,谨致谢意.
[1] BONDY J A, MURTY U S R. Graph Theory with Application[M]. New York:Elsevier,1976:1-20.
[2] MERRIFIELD R E, SIMMONS H E. Topological Methods in Chemistry[M]. New York:Wiley Inter Science,1989:1-15.
[3] ZHAO H X, LI X L. On the fibonacci numbers of trees[J]. Fibonacci Quarterly,2006,44(1):32-38.
[4] 南基洙. 组合数学[M]. 北京:高等教育出版社,2008:108-119.
[5] 周旭冉,王力工. 聚苯链Hosoya的指标的计算[J]. 山西大学学报(自然科学版),2011,34(2):180-184.
[6] REN S Z, WU T Z. Hosoya index ofL-type polyphenyl spiders[J]. J Chemistry,2016,2016(9):1-5.
[7] PRODINGER H, TICHY R F. Fibonacci numbers of graphs[J]. Fibonacci Quarterly,1982,20(1):16-21.
