某型机主起落架可折机构挠度计算系统研究与应用

田 俊，潘 浩，潘平逊，占金青

（1.凌云科技集团有限责任公司技术中心，湖北 武汉 430001；2.华东交通大学机电与车辆工程学院，江西 南昌 330013）

1 引言

2 建立主起落架数字样机

某大型运输机的可折撑杆是实现主起落架系统收放的空间连杆机构，该机构展开时可折撑杆形成的向上挠度是保证运输机起飞和着陆安全的关键指标之一[1]。在大修装配时需通过调节支臂上齿板扣齿长度，将可折撑杆向上挠度调整到规定范围内。由于缺少计算方法，在实际维修时通常采用“装配—测量—不合格拆卸—返回车间调试—再装配”循环迭代的生产方式，导致维修周期不稳定，影响飞机交付时间。生产一线需要能够在主起落架装配前根据零部件实际测量尺寸准确计算可折撑杆向上挠度并反求支臂调节量的方法。

2.1 机构运动学简析

对该型运输机主起落架收放机构进行适当的简化，得到机构简图，如图1所示。

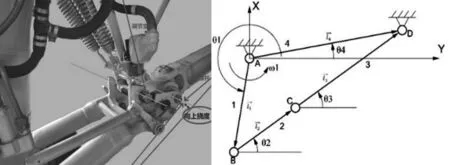
图1 主起落架可折机构分析简图Fig.1 Analysis Diagram of Main Undercarriage Foldable Mechanism

图中：1—缓冲支柱；2—斜撑杆；3—前撑杆；4—机身安装位置形成的空间距离。

当起落架收起时，铰链点C将向上运动。对于空间连杆机构，已知输出端的位置，求解从输入端到各个关节的位置和状态参数是机构位置逆解问题，该主起落架装配过程支臂调节量的计算就属于此类机构位置逆解问题。

对机构逆解的求解方法主要有图解法和解析法。其中，解析法又分为矢量解析法、复数法和矩阵法[2]。结合三维模型和解析法，可分析机构在整个运动过程的几何特性[3]，可理解为零部件在不同尺寸下的装配状态。如图1所示，建立主起落架杆系坐标系，将各构件表示为杆矢，各杆矢的方位角均由x轴正向开始，沿逆时针方向为正，该机构封闭矢量方程为：

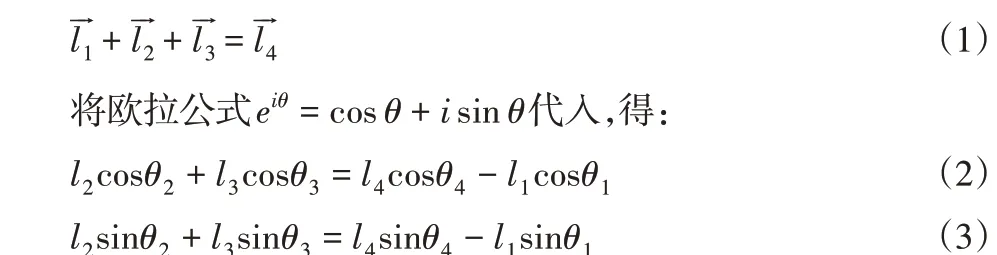
式中：l1、l2、l3和l4—图1中1杆、2杆、3杆和4杆的长度；θ1、θ2、θ3和θ4—图1中1杆、2杆、3杆和4杆的方位角。其中，l4和θ4代表固定装机位置，取为常数。

通过以上各参数在取值范围内的计算，可得该机构杆件主要杆件几何尺寸与装配指标的数值关系。

2.2 建立主起落架数字样机

明确主起落架工作原理和结构形式后，建立了包括主起落架缓冲支柱、带锁可折撑杆、主起落架收放作动筒、机轮、稳定缓冲器等部件的三维模型。按运动属性定义部件分组[4−5]，建立了主起落架三维数字样机，通过运动过程干涉检查验证了样机装配正确性。将各零部件尺寸设定为名义尺寸，采用运动仿真模块，驱动输入端收放作动筒活塞运动副实现了主起落架收放过程运动仿真。主起落架收起过程中收放作动筒活塞杆位移与前撑杆转动位移、缓冲支柱转动位移之间的关系，如图2所示。

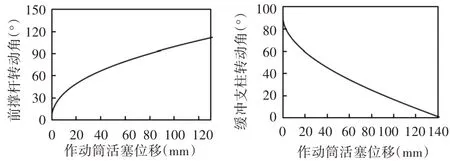
图2 活塞杆驱动位移与撑杆转角变化关系Fig.2 Input−Output Relationship of Foldable Mechanism

3 装配位置分析研究

3.1 建立装配位置分析模型

基于主起落架数字样机，从数字样机中提取出主起落架机构装配位置分析模型，如图3所示。其中，装配位置模型定义如下：

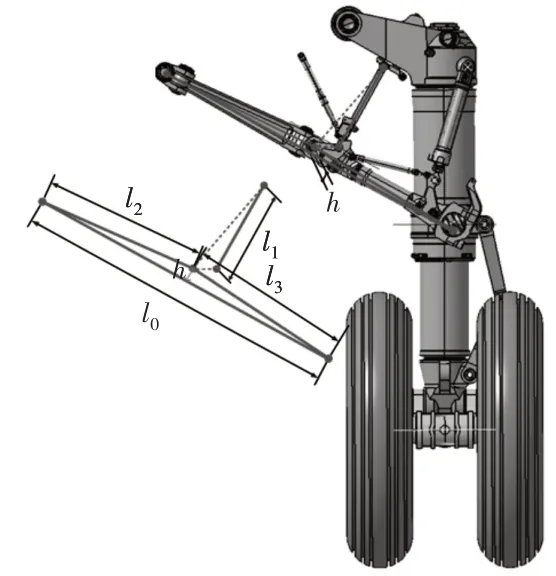
图3 基于机构运动学建立装配位置分析模型Fig.3 Modeling of Assembly Positioning Analysis

（1）自变量：调节支臂轴心距l1、前撑杆轴心距l2、斜撑杆轴心距l3；

（3）目标函数：4.0mm ≤可折撑杆向上挠度h≤5.3mm；

（4）约束条件：与机身固定位置对接（与真实装机环境保持一致）、满足零部件装配关系。

3.2 数字样机二次开发

利用三维软件提供的二次开发接口，使用宏命令对数字样机进行参数定义、数据传递和计算分析[6−7]。利用VBA程序开发数据录入和计算结果反馈的人机交互界面，如图4所示。

图4 分析模型与数字样机的数据关联Fig.4 Data Connection Between Modeling and Programming

通过计算程序将装配位置分析模型中定义的参数与三维模型中对应的形位尺寸进行数据关联[8]，不仅实现了向三维模型相关尺寸传递其实测数值，实时更新模型中装配状态的效果，而且实现了从三维模型提取装配分析模型自变量的数值，利用参数化程序研究各参数与关键装配指标关系的功能。通过对仿真试验的数据进行拟合分析，得到回归的函数解析式，形成调节支臂长度的控制规律。

3.3 可折机构的参数敏感性研究

3.3.1 调节支臂轴心距l1与撑杆向上挠度h关系

保持前撑杆轴心距l2和斜撑杆轴心距l3不变，通过程序计算调节支臂轴心距l1为不同数值时对应的撑杆向上挠度h，分析对象和计算结果，如图5（a）所示。

对计算结果采用h=a1l1+b1拟合h=f1( )l1函数，其中，a1—拟合斜率；b1—拟合截距。通过最小二乘法得到a1=−1.1751，b1=428.825。

3.3.2 前撑杆轴心距l2与撑杆向上挠度h关系

保持调节支臂轴心距l1和斜撑杆轴心距l3不变，通过程序计算前撑杆轴心距l2为不同数值时对应的撑杆向上挠度h，分析对象和计算结果，如图5（b）所示。对计算结果采用h=a2l2+b2拟合h=f2(l2)函数，其中，a2—拟合斜率；b2—拟合截距。通过最小二乘法得到a2=−0.5243，b2=337.0593。

3.3.3 斜撑杆轴心距l3与撑杆向上挠度h关系

保持调节支臂轴心距l1和前撑杆轴心距l2不变，通过程序计算斜撑杆轴心距l3为不同数值时对应的撑杆向上挠度h，分析对象和计算结果，如图5（c）所示。对计算结果采用h=a3l3+b3拟合h=f3(l3)函数，式中：a3—拟合斜率；b3—拟合截距。通过最小二乘法得到a3=−0.5161，b3=315.7913。

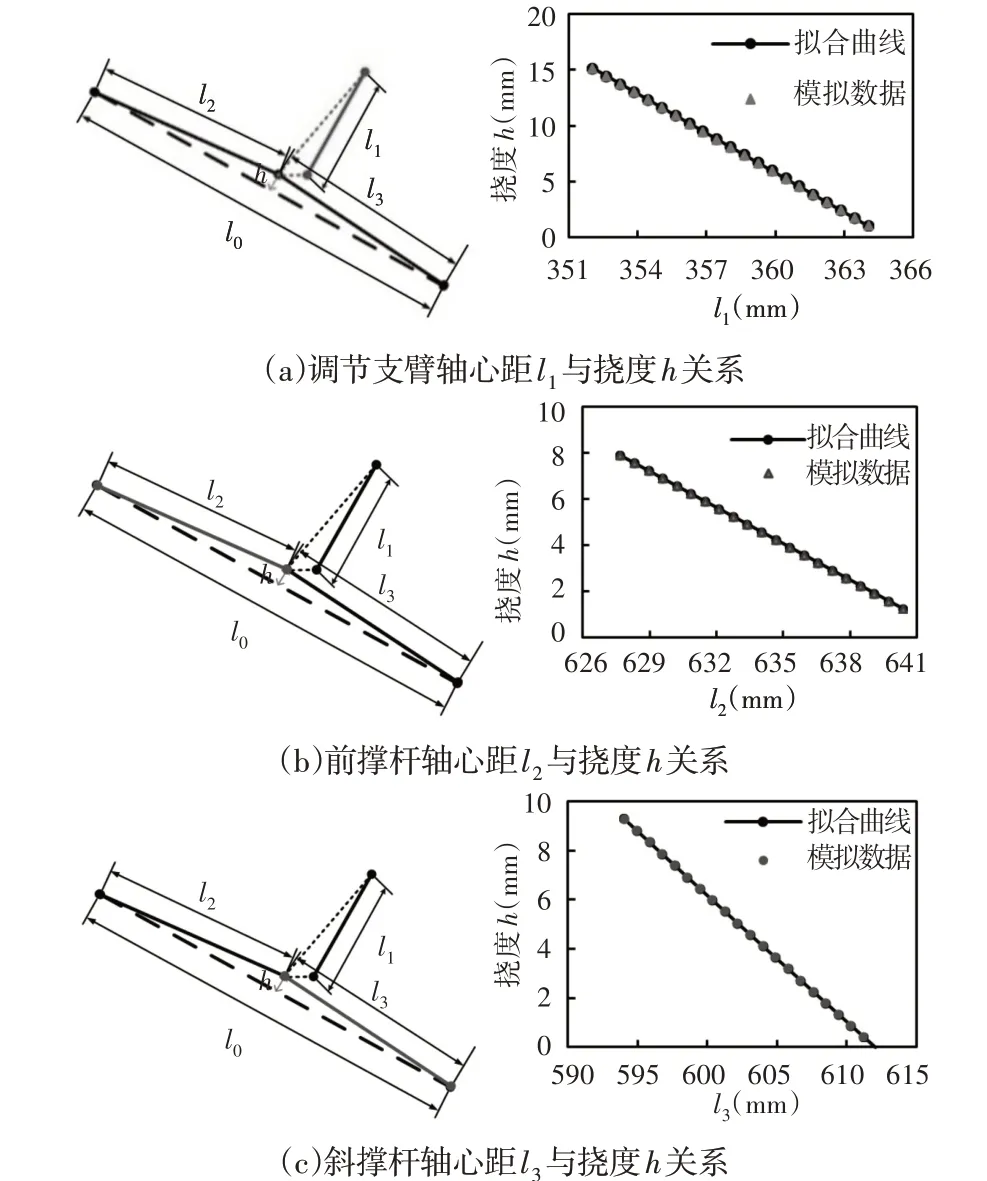
图5 可折机构参数敏感性研究Fig.5 Relation Between Mechanism Parameters and Deflection h

4 应用开发与工程验证

4.1 滚轮间隙影响分析

根据主起落架可折撑杆锁机构功能特点，分别计算了当调节支臂轴心距l1、前撑杆轴心距l2和斜撑杆两端轴心距l3为名义尺寸时，锁机构的滚轮轴心与卡槽轴心对齐的理想状态、滚轮与卡槽顶面相切和滚轮与卡槽底面相切三种状态的可折撑杆挠度数值，如图6所示。仿真和测试结果都表明，滚轮与卡槽顶面相切时的挠度比理想轴心对齐状态的挠度要小。计算程序将该间隙作为输入参数之一，可根据现场塞尺测量值计算得到更贴合实际情况的撑杆向上挠度。

图6 滚轮与卡槽底面相切状态Fig.6 Tangent Status Between Roller and Slot

4.2 应用开发

结合生产现场应用场景，设计了应用流程及交互界面，测量现场及程序交互界面，如图7所示。主要应用步骤为：

图7 应用程序交互界面Fig.7 Interface Development and Application

（1）现场测量主起落架前撑杆轴心距l2和斜撑杆轴心距l3；

（2）将前撑杆轴心距l2和斜撑杆轴心距l3实测值输入挠度计算系统，主起落架数字样机状态实时更新；

（3）根据调节支臂轴心距l1与可折撑杆向上挠度h的函数关系，可求得满足要求的调节支臂轴心距l1取值范围(l1min～l1max)；

（4）以调节支臂轴心距l1取值范围(l1min～l1max)为指导，根据产品实际情况，选择范围内的可取的调节支臂长度l′1，计算该装配状态下的可折撑杆挠度值h和可折撑杆中心距l0，并将计算值和测量数据录入维修工卡。

4.3 工程验证

根据现场测量的前撑杆轴心距l2=635.0mm、斜撑杆轴心距l3=603.1mm，输入程序计算得到满足可折撑杆向上挠度h要求的调节支臂轴心距l1取值范围为（361.044～362.148）mm。以计算结果为指导、根据产品实际情况，在安装现场将调节支臂调节到l1=361.5mm，实测可折撑杆向上挠度h=4.7mm，满足装配要求，验证了主起落架可折撑杆机构挠度计算系统能有效的辅助装配工作。经相关部门技术鉴定，该主起落架可折撑杆机构挠度计算系统已应用于某型运输机主起落架维修，该技术方案可推广至其他机型主起落架装配工作。

5 总结

针对某大型运输机大修主起落架装配时可折撑杆向上挠度反复调试的问题，开展数字化辅助修理技术应用研究。结合主起落三维模型和机构运动分析方法，研究了主要零部件尺寸参数与装配要求之间的数学关系。基于机构优化设计思想，建立了反映主要零部件尺寸与关键指标的装配位置分析模型。通过程序开发出一套可实现测量数据输入、数值传递、模型状态更新、计算分析和结果输出的应用程序。经相关验证与鉴定，该主起落架可折撑杆挠度计算系统可以辅助主起落架装配校准和调整工作，有效地减少拆装次数，缩短调试时间，提高维修效率。