一种分析并联机构输出运动能力特性的新方法

罗建国，李 攀，邱杰清，赵韵秋

（1.华北科技学院机电工程学院，北京 101601；2.河北省矿山设备安全监测重点实验室，北京 101601；3.华北科技学院研究生院，北京 101601）

1 引言

在工业机器人产品的开发流程中，运动学和动力学分析是验证新型动作机构设计方案可行性的必需环节。具备典型的工艺轨迹作为机器人产品能够实现预定功能的先决条件，也是使用动力学模型进行仿真计算的重要依据。因此，在满足产品基础设计的条件下，完成机器人动作机构运动轨迹的规划便形成了机构运动仿真分析的理论基础和前提，而求解机构的自由度对于判断所设计的机构是否具有唯一的运动轨迹至关重要，也是分析机构运动能力特性的关键指标。当前流行的自由度计算公式和方法主要是以古典机构和并联机构为研究对象来开展的［1］。文献［2］于1983年首次提出一种3自由度并联机构以来，很多学者在机构自由度分析领域做出了重要的贡献，然而，计算一般机构自由度所采用的G−K公式在机构设计过程中却难以得到正确应用，复杂机构运动特性分析过程中存在的缺陷和问题目前仍未得到有效地解决。在这种背景下，开发一种可靠的并联机构自由度计算理论并促生行之有效的机构运动能力特性分析方法，亦因此成为机构设计工程领域的研究热点。

目前，已有众多学者就如何精确求解并联机构的自由度提出了一些列方法。文献［3−4］提出的基于约束螺旋理论的自由度分析方法和修正G−K公式，能够有效地对并联机构的自由度进行数值求解并且具备良好的通用性。文献［5］建立了并联机构的新字符描述，采取螺旋参数化表达结合字符描述的手段完成了分支运动螺旋系的自动求解，并且基于线性代数中的初等行变换和含“未定几何关系”轴线之间的相对自由度，实现了空间并联机构的自由度数字化自动分析。文献［6］基于分形理论和机构拓扑图，提出了一种简单有效的混联机器人构型综合理论和设计方法，并以三平移三自由度混联机构为例对该方法的正确性进行了检验。文献［7］提出了一种可重构空间五杆机构，且利用螺旋理论分析和证明了可重构并联机构可以实现四种不同的运动模式。文献［8］基于R（3，3）几何代数空间，提出了一种符号描述并联机构自由度的自动化分析算法，对于分析机构在特定参数和位置情况下的自由度及运动情况十分有利。文献［9］提出了一类含较少运动副的四支链两转一移三自由度并联机构，并基于极限约束力螺旋系的概念对所提出并联机构的运动副数目是否为同类机构中最少进行了论证。

然而，现有的机构自由度计算方法及公式仍存在不足之处，主要体现在：（1）自由度计算结果的形式单一。现有的计算方法多专注于机构自由度的数值计算，未能兼顾符号解或者解析表达式的输出形式；（2）计算结果模糊。机构分支的自由度在很大程度上体现着其对于输出构件的约束作用，基于“集合求交运算避开过约束”原理的自由度计算方法往往用于机构整体自由度的计算，而一般的方法和公式未能避免过约束的重复计算，以至于影响了计算精度［10］。

值得一提的是，混联机构覆盖了并联机构刚性好、精度高以及串联机构运动空间大、灵巧性好的优点，同时又回避了单纯串、并联机构各自的缺点，极大提高了机器人机构设计对于产品性能需求的适应性，在学术界和工业领域得到了广泛关注，已发展成机构学研究领域的一个重要研究方向［11］。

以有效和系统地分析并联机构的输出运动能力特性为目标，提出了基于“最短支链∕支链对”的“木桶原理分析法”。研究过程通过运用主−副运动理论和机构输入−输出运动综合转化公式，导出并联机构的输出运动特性的一般计算结果表达式，并使用修正的G−K 公式对7 种不同姿态下的SPS∕SPU∕UPS 结构的4−6 支链并联机构的输出运动特性进行了分类对比研究，得到了并联机构输出运动能力特性的影响因素和规律。借助等效串联机构、广义等效串联机构分别描述并联机构和混联机构，并以实例演示了机构输出运动能力特性的计算分析方法和结果。

采用的有关方法和结论为研究并联机构、混联机构输出运动特性及其具体构成、工作空间、奇异、耦合性等提供了一体化系统分析途径，进一步丰富了机构设计工程领域的理论内容，对于机器人产品的设计和制造具有重要的应用价值和研究意义。

2 随运动综合转化公式

基于主−副运动理论，串联机构或并联机构的单一支链所对应的输入−输出运动综合转化公式的基本形式如式（1）～式（6）所示。

一阶伴随输出平移运动计算公式如下：

有关一阶、二阶伴随运动存在性，三阶及以上伴随运动的不存在性，其他情形的输入−输出运动综合转化的过程和规律参照以上过程，在此不再赘述。

3 一类并联机构的构型与姿态

关节、支链是串联机构、并联机构、混联机构的基本组成元素，根据关节和支链的不同，对不同类型和情形的并联机构形式进行了定义，从而可为后续过程中，基于主−副运动理论、支链输入−输出运动综合转化公式对由SPS∕SPU∕UPS结构组成的4−6支链并联机构的自由度进行计算分析奠定概念基础。

首先，定义两种构型的并联机构形式：

A构型并联机构：4−6支链a−SPS−b−SPU或者a−SPS−b−UPS并联机构（其中a≥0，b≥1，a+b=n，n=4∕5∕6）。

B构型并联机构：完全由SPS支链组成的4−6支链并联机构n−SPS（n=4∕5∕6）。

其次，设定X1为支链与静平台的关节铰接点，X3为支链与动平台的关节铰接点，O、E分别为静平台、动平台的形心，定义七种并联机构的空间结构姿态：

C1态：并联机构各支链所在直线X1X3与X1O构成的所有平面中有1个平面与静平台所在的水平面Oxy垂直，且X1O与X3E有1组平行，如图1所示。

图1 A∕B构型并联机构处于C1态示意图Fig.1 The Schematic Diagram of A∕B Parallel Mechanism in C1 State

C2态：并联机构各支链所在直线X1X3与X1O构成的所有平面中有2个平面与静平台所在的水平面Oxy垂直，且2个铅垂面之间也相互垂直。另外，X1O与X3E有2组平行，且位于动静平台上的这两组直线在各自平面内相互垂直，如图2所示。

图2 A∕B构型并联机构处于C2态示意图Fig.2 The Schematic Diagram of A∕B Parallel Mechanism in C2 StateC3态：并联机构各支链所在直线X1X3与X1O构成的所有平面中有1个平面与静平台所在的水平面Oxy垂直，但X1O与X3E均不平行，如图3所示。

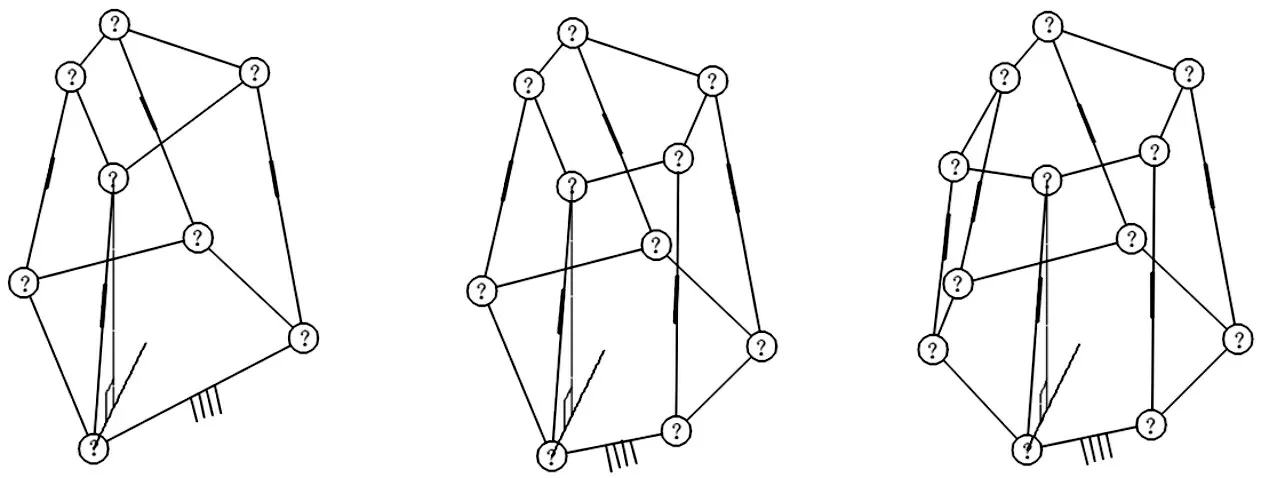
图3 A∕B构型并联机构处于C3态示意图Fig.3 The Schematic Diagram of A∕B Parallel Mechanism in C3 State

C4态：并联机构各支链所在直线X1X3与X1O构成的所有平面中有2个平面与静平台所在的水平面Oxy垂直，且2个铅垂面之间也相互垂直，但X1O与X3E均不平行，如图4所示。

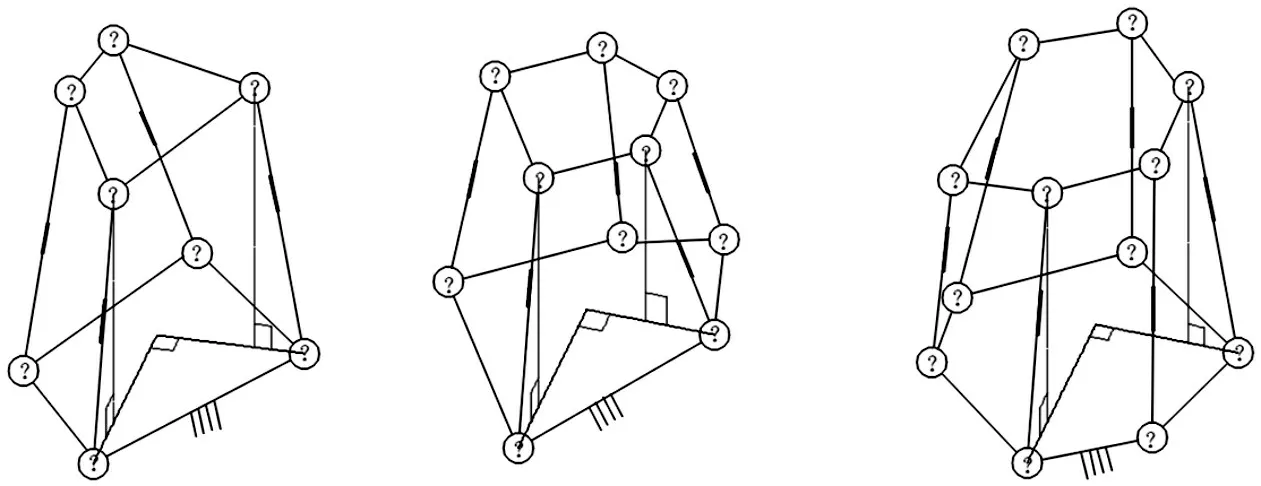
图4 A∕B构型并联机构处于C4态示意图Fig.4 The Schematic Diagram of A∕B Parallel Mechanism in C4 State

C5态：并联机构各支链所在直线X1X3与X1O构成的所有平面与静平台所在的水平面Oxy均不垂直，但X1O与X3E有1组平行，如图5所示。

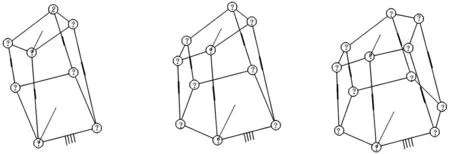
图5 A∕B构型并联机构处于C5态示意图Fig.5 The Schematic Diagram of A∕B Parallel Mechanism in C5 State

C6 态：并联机构各支链所在直线X1X3与X1O构成的平面与静平台所在的水平面Oxy均不垂直，但X1O与X3E有2 组平行，且位于动静平台上的这两组直线在各自平面内相互垂直，如图6所示。

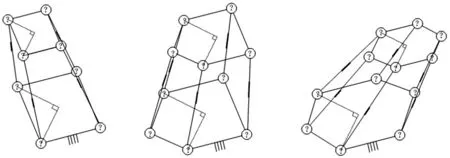
图6 A∕B构型并联机构处于C6态示意图Fig.6 The Schematic Diagram of A∕B Parallel Mechanism in C6 State

C7态：并联机构各支链所在直线X1X3与X1O构成d的平面与静平台所在的水平面Oxy均不垂直，且X1O与X3E均不平行，如图7所示。

图7 A∕B构型并联机构处于C7态示意图Fig.7 The Schematic Diagram of A∕B Parallel Mechanism in C7 State

4 并联机构输出运动能力特性“木桶原理分析法”

由木桶效应的含义可知，构成组织的各个部分往往是优劣不齐的，而劣势部分往往决定整个组织的水平。根据木桶原理的短板理论，针对有效和系统地分析并联机构运动能力特性的问题，提出了基于“最短支链”或“最短支链对”的“木桶原理分析法”。

4.1 基本概念与方法

并联机构输出运动能力特性由各支链输出运动能力特性的交集综合而成。将受限最多且自身输出运动能力空间维度最少、同时与其他支链拥有最少共同输出运动能力特性的支链定义为“最短支链”。若同时存在2条及以上的“最短支链”，且该两条支链相互间还存在特殊的空间构造关系，则选取其中最有代表性且构造关系特殊的2条支链组成“最短支链对”。“最短支链”或“最短支链对”的输出运动能力特性对并联机构的输出运动能力特性具有决定作用，即：（1）当并联机构各组成支链具有相同的结构形式时，并联机构输出运动能力特性则取决于空间位置和姿态受到约束限制最多的支链，若有1条支链属于特殊状态，那么，就可以对这一输出运动能力空间维度最少的支链展开分析，用其运动能力特性的分析结果来等效获得并联机构的输出运动能力特性；（2）当有2条支链处于空间特殊状态时，这2条支链的输出运动受限最多，则通过对这2条支链进行综合分析，将所有约束运动去除后即可得到等效并联机构的输出运动能力特性。因此，通过对该1条或2条支链运动能力特性进行分析，便可以获得整个并联机构的输出运动能力特性结果。

将这种通过分析并联机构“最短支链”或“最短支链对”（简写为“最短支链／支链对”）的输出运动能力特性结果，进而等效获得对应并联支链输出运动能力特性的方法被定义为“木桶原理分析法”。应用提出的“木桶原理分析法”，分析并联机构输出运动能力特性的具体步骤如下：

（1）依据并联机构输出运动能力特性合成的“木桶原理”，确定此时机构的“最短支链”。

（2）将固定坐标系的构建与“最短支链”关联起来，尽量使固定坐标系的水平轴与“最短支链”或“最短支链对”分别处于三维直角坐标系的两个铅垂面上，并确定对应的输入运动分量和主输出运动分量。

（3）根据“最短支链”两端的关节铰点分别与静平台、动平台各自形心的连线是否平行，判别该广义2转动串联机构的第2级杆的杆长是否退化为零。

若上述的这两条连线平行，则该广义2转动串联机构的第2级杆的杆长退化为零，此时不存在由2个转动输入运动综合而成的一阶伴随移动运动。

（4）依据“最短支链／支链对”输入运动分量，分析并确定“最短支链／支链对”全部一阶伴随输出运动分量。

（5）依据“最短支链／支链对”的输入运动分量及其全部一阶伴随运动，对其二阶伴随输出运动分量进行判别分析。

（6）综合（2）～（5）的结果，得到代表并联机构输出运动能力特性的“最短支链／支链对”的输出运动能力特性的全部构成，获得并联机构对应的主输出运动自由度M−DOF、伴随输出运动自由度P−DOF（通过伴随运动性质和空间维度来区分，但是不区分一阶、二阶伴随运动，按空间三维转动、三维移动的吸收原则和合并原则得到）、输出运动自由度O−DOF（通过输出运动性质和空间维度来区分，但是不区分主运动、伴随运动，按空间三维转动、三维移动的吸收原则、合并原则得到）。

情形1−1（Q11）：A 构型并联机构（P（A）），同时处于C1 态（C1），描述为Q11=P(A)⊕C2，如图1所示。

按照前面给出的方法分析可以得知：

（4）由n条支链构成的并联机构的输出运动能力特性，可以由构成该并联机构的n条支链的输出运动能力特性的交集综合运算分析得到，其表达式如式（10）所示。

4.2 实例分析

并联机构中，第K条支链的输入运动能力转化为输出运动能力特性的过程以式（7）表示。其中，第K条支链的输入运动能力特性由支链上的S、P、U关节的输入运动能力特性集合而成，如式（8）所示。

此时并联机构的M−DOF=5、P−DOF=3、O−DOF=5。

情形1−2（Q12）：A 构型并联机构（P（A）），同时处于C2 态（C2），描述为Q12=P(A)⊕C2，如图2所示。

依据前述方法分析可知：

（1）依据选取的“最短支链对”的空间状态，将固定坐标系的x轴、y轴分别与两正交铅垂平面和水平面的交线重合，该“最短支链对”移动关节的运动所沿着x轴、y轴方向的分量将均不存在，故只有沿着z轴方向的移动运动分量。

（2）“最短支链对”由于2个平行绕x轴、y轴的转动输入而产生的沿着y轴、x轴方向的一阶伴随移动输出运动不存在，只有沿着z轴方向的一阶伴随移动输出。

（3）对支链上各关节输入运动与一阶伴随输出运动进行综合分析，可知“最短支链对”不存在二阶伴随输出运动。

结合前面分析结果得到“最短支链对”的输出运动能力特性结果表示，如式（11）所示。

此时并联机构的M−DOF=4、P−DOF=1、O−DOF=4。

情形1−3（Q13）：B 构型并联机构（P（B）），同时处于C1 态（C1），描述为Q13= P(B)⊕C1，如图1所示。

借鉴情形1−1的分析过程和方法，可以得知：

（1）“最短支链”为SPS构造，将固定坐标系的x轴与两垂直平面构成平面的交线重合，该支链沿着y轴方向移动输入运动分量将不存在，而有沿着x、z轴方向的移动运动分量。

（2）“最短支链”有2个平行绕x轴的转动输入而产生的沿着y、z轴方向的一阶伴随移动输出运动将不存在，但由于两个平行绕y轴的转动输入而产生的沿着x、z轴方向的一阶伴随移动输出运动将存在。

且两个平行绕z轴的转动输入而产生的沿着x、y轴方向的一阶伴随移动输出运动也将存在，所以该支链具有沿着x、y、z轴方向的一阶伴随移动输出运动。

（3）对支链上各关节输入运动与一阶伴随输出运动做进一步综合分析，可以得知支链存在绕x、y、z轴的二阶伴随转动输出运动。

将此时的并联机构视为一个等效串联机构，并联机构输出运动能力特性表示如式（13）所示。

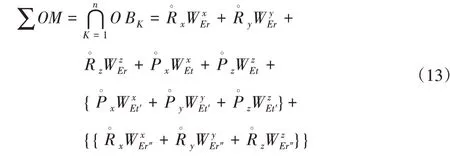
此时并联机构的M−DOF=5、P−DOF=6、O−DOF=6。

情形1−4（Q14）：B 构型并联机构（P（B）），同时处于C2 态（C2），描述为Q14= P(B)⊕C2，如图2所示。

借鉴情形1−2的分析过程和方法，可以得知：

（1）“最短支链对”均为SPS构造，将固定坐标系的x轴、y轴分别与两正交铅垂平面和水平面的交线重合，该“最短支链对”移动关节的运动所沿着x轴、y轴方向的分量都将不存在，而只有沿着z轴方向的移动运动分量。

（2）“最短支链对”有2组分别平行绕x、y轴的转动输入而产生的沿着y、x轴方向的一阶伴随移动输出运动将不存在，由于两个平行绕z轴的转动输入而产生的沿着x、y轴方向的一阶伴随移动输出运动还将存在，所以该“最短支链对”仍具有沿着x、y、z轴方向的一阶伴随移动输出。

（3）对支链上各关节输入运动与一阶伴随输出运动进行综合分析，可知“最短支链对”存在绕x、y轴的二阶伴随转动输出运动。

结合前面分析结果得到“最短支链对”所代表的并联机构输出运动能力特性结果表示如式（14）所示。

此时并联机构的M−DOF=4、P−DOF=5、O−DOF=6。

机构中存在相当数量的不起限制作用的过约束，但一般的自由度计算公式将这部分自由度重复计算，从而导致自由度计算不能得到正确的结果。

鉴于修正的G−K公式在进行并联机构自由度数值求解方面的有效性和良好的通用性，将借助修正的G−K公式对所列4种情形的机构自由度进行计算，并将计算结果与采用所提出的并联机构输出运动能力特性分析方法得到的分析结果进行对比研究，从而可以对上述4种情形分析结果的正确性进行验证。

经过黄真修正的G−K公式如下：

式中：M—机构自由度数目；n—构件数目；g—运动副数目；fi—第i个运动副的自由度数目；d—机构的阶数；λ—公共约束数目；ν—多环并联机构在公共约束因素后的冗余约束数目；ζ—机构的局部自由度数目。

式（10）、式（12）、式（14）提出的并联机构输出运动能力特性“木桶原理分析法”结合主−副运动理论和机构输入−输出综合转化公式分析得来，是并联机构在4种情形下的输出运动能力特性一般计算结果的表达式。

对于上述4种情形并联机构形式，分别采用修正的G−K公式和机构输出运动能力特性一般计算结果的表达式对并联机构的自由度进行计算分析，计算结果对比，如表1所示。

由表1可知，采取机构输出运动能力特性表达式计算所得的机构自由度结果包括M−DOF、P−DOF和O−DOF。而基于修正的G−K公式计算所得的自由度分析结果则只有一个（M），且该结果与基于输入−输出运动综合转化公式计算所得机构自由度结果中的M−DOF相同。因此，经过比较可以发现：在机构自由度分析方面，基于输入−输出运动综合转化公式的机构自由度分析方法表现的更加全面、深入和具体，其能够有效弥补现有并联机构自由度分析理论的不足，可以为并联机构工作空间、奇异、耦合特性的一体化系统研究提供更加适当的途径。

表1 A/B构型并联机构在C1/C2状态下的自由度分析Tab.1 DOF Analysis of A/B Parallel Mechanism in C1/C2 State

参照4 种情形给出如下定义：Q21=P(A)⊕C3、Q22=P(A)⊕C4、Q23=P(B)⊕C3、Q24=P(B)⊕C4，借鉴参考对应的分析方法，采用修正的G−K公式进一步对其验证分析，得到如表2所示的有关结论。

表2 A/B构型并联机构在C3/C4状态下的自由度分析Tab.2 DOF Analysis of A/B Parallel Mechanism in C3/C4 State

同理，可以给出如下定义：Q31=P(A)⊕C5、Q32=P(A)⊕C6、Q33=P(B)⊕C5、Q34=P(B)⊕C6，借鉴对应的分析方法，得到如表3所示的有关结论。

表3 A/B构型并联机构在C5/C6状态下的自由度分析Tab.3 DOF Analysis of A/B Parallel Mechanism in C5/C6 State

此外，还可以给出情形4−1（Q41）的定义：A构型并联机构或者B 构型并联机构（P(A∕B)），同时处于C7 状态（C7），描述为Q41=P(A∕B)⊕C7，如图7所示。

此时，并联机构各支链上均存在沿x、y、z轴方向的移动输入运动和绕x、y、z轴的转动输入运动。通过各支链输出末端运动能力特性的交集综合计算分析，可知并联机构存在沿x、y、z轴方向的一阶伴随移动输出运动，存在绕x、y、z轴的二阶伴随转动输出运动，其输出运动能力特性的一般表示如式（16）所示。

对该情形的并联机构采用修正的G−K公式计算分析，得到的有关结论，如表4所示。

表4 A/B构型并联机构在C7状态下的自由度分析Tab.4 DOF Analysis of A/B Parallel Mechanism in C7 State

根据表1～表4内的比较结果显示：

（1）m−SPU−n−SPS∕m−UPS−n−SPS（m≥1，n≥0，m+n=4∕5∕6）并联机构处于不同的空间姿态和构造形态时，其自由度主要受两个因素的影响：①由支链所在的直线、支链静平台连接点与静平台形心的连线所构成的平面，与静平台所在的平面是否垂直；②由支链静平台连接点和静平台形心所形成的连线，与由同一支链动平台连接点和动平台形心所形成的连线是否平行。该并联机构处于C1、C2两种状态时，M−DOF=4∕5，P−DOF=1∕3，O−DOF=4∕5；处于C3、C4两种状态时，M−DOF=4∕5，P−DOF=5∕6，O−DOF=6；处于C5、C6 两种状态时，M−DOF=6，P−DOF=3∕5，O−DOF=6；处于C7状态时，M−DOF=6，P−DOF=6，O−DOF=6。

（2）并联机构n−SPS（n=4∕5∕6）处于不同空间姿态和构造形态时，其自由度同样受两因素影响：①由支链所在直线、支链静平台连接点与静平台形心的连线所构成的平面，与静平台所在的平面是否垂直；②由支链静平台连接点和静平台形心所形成的连线，与由同一支链动平台连接点和动平台形心所构成的连线是否平行。该并联机构处于C1、C2、C3、C4四种状态时，M−DOF=4∕5，P−DOF=5∕6，O−DOF=6；处于C5、C6两种状态时，M−DOF=6，P−DOF=5∕6，O−DOF=6；处于C7状态时，M−DOF=6，P−DOF=6，O−DOF=6。

（3）基于支链输入−输出运动综合转化公式进行求交综合运算所得到并联机构的M−DOF、P−DOF、O−DOF具体数值，与通过修正的G−K公式计算得到的机构自由度分析结果M值不完全相同，表现为：有的M值与O−DOF数值相同，有的M与M−DOF数值相同。其原因是G−K公式不能揭示输入运动与输出运动之间的综合转化关系和规律。

深入探索以上对比研究分析的结果，可以总结得到并联机构输出运动能力特性的影响因素和规律，即：（1）水平面内一个或两个方向的主输出移动运动是否存在由支链的空间姿态决定；（2）水平面内一个方向的一阶伴随移动运动是否存在取决于动平台的空间姿态；（3）动平台上的关节位置、动平台结构和动平台的空间姿态共同决定了水平面内2个方向的一阶伴随移动运动是否存在；（4）构建固定坐标系使某一个或两个支链分别位于其铅垂面上，可令机构水平面内1个或2个输出主运动分量消失；而选择静平台平面与固定坐标系的水平面重合，能达到使机构水平面内1个或2个一阶伴随移动输出分量消失的效果。

5 混联机构输出运动能力特性分析

混联机构兼具串联和并联机构的优点，令其具备较高的开发价值和推广前景。依据串联机构与并联机构的连接方式不同，可以将混联机构分成三类，即：串−并−串、并−串−并、并−串式（等同于串−并式）。将机构的运动关节以方框代替，并以线段连接表示机构的支链，以此来绘制机构的平面拓扑示意图。其中，串联、并联机构的平面拓扑示意图，如图8、图9所示。并−串−并、并−串、串−并−串形式混联机构拓扑示意图，如图10～12所示。并联机构的等效串联机构或关节拓扑示意图，如图13所示。图10、图11、图12所对应的混联机构的广义等效串联机构拓扑示意图，如图14～图16所示。

图8 串联机构拓扑示意图Fig.8 The Topological Schematic Diagram of Series Mechanism

图9 并联机构拓扑示意图Fig.9 The Topological Schematic Diagram of Parallel Mechanism

图10 并−串−并形式混联机构拓扑示意图Fig.10 The Topological Schematic Diagram of Hybrid Mechanism with Parallel−Series−Parallel Forms

图11 并−串形式混联机构拓扑示意图Fig.11 The Topological Schematic Diagram of Hybrid Mechanism with Parallel−Series Forms

图12 串−并−串形式混联机构拓扑示意图Fig.12 The Topological Schematic Diagram of Hybrid Mechanism with Series−Parallel−Series Forms

图13 并联机构的等效串联机构或关节拓扑示意图Fig.13 The Topological Schematic Diagram of Equivalent Series Mecha⁃nism or Joint of Parallel Mechanism

图14 并−串−并形式混联机构广义等效串联机构拓扑示意图Fig.14 The Topological Schematic Diagram of Generalized Series Mech⁃anism of Hybrid Mechanism with Parallel−Series−Parallel Forms

图15 并−串形式混联机构广义等效串联机构拓扑示意图Fig.15 The Topological Schematic Diagram of Generalized Series Mech⁃anism of Hybrid Mechanism with Parallel−Series Forms

图16 串−并−串形式混联机构广义等效串联机构拓扑示意图Fig.16 The Topological Schematic Diagram of Generalized Series Mech⁃anism of Hybrid Mechanism with Series−Parallel−Series Forms

针对2SPS−3SPU−RR 混联机构，建立的直角固定坐标系，可知该机构由并联机构2SPS−3SPU和串联支链RxRy构成，如图17所示。

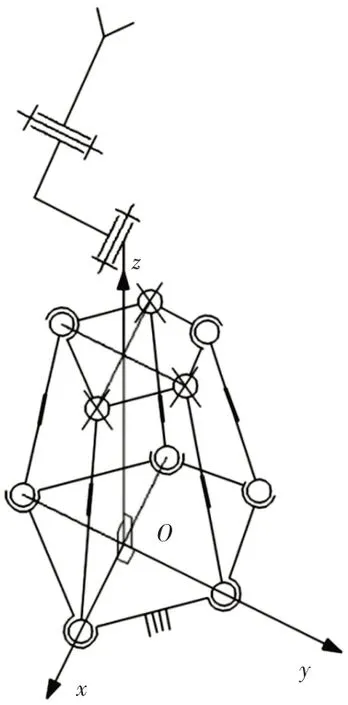
图17 2SPS−3SPU−RR混联机构Fig.17 2SPS−3SPU−RR Hybrid Mechanism

假设并联机构2SPS−3SPU满足前面分析Q12= P(A)⊕C2条件，串联支链上的转动关节轴线分别平行于固定坐标系的x、y轴。借助表1中Q12= P(A)⊕C2的分析结论，可得机构并联部分的输出运动能力特性可用式（17）表示。

混联机构的广义等效串联机构Gs的输出运动能力特性可以通过输入−输出运动综合转化公式计算得到，如式（19）所示。其中，符号“Δˉ”代表运动元素域移动运算，符号“Δ̑”代表运动元素域转动运算，符号“⋃”代表运动元素域并运算，对应运动域括号外的下标()x、()y、()z表示只选取运动沿着或绕该下标所示轴方向的区间域。

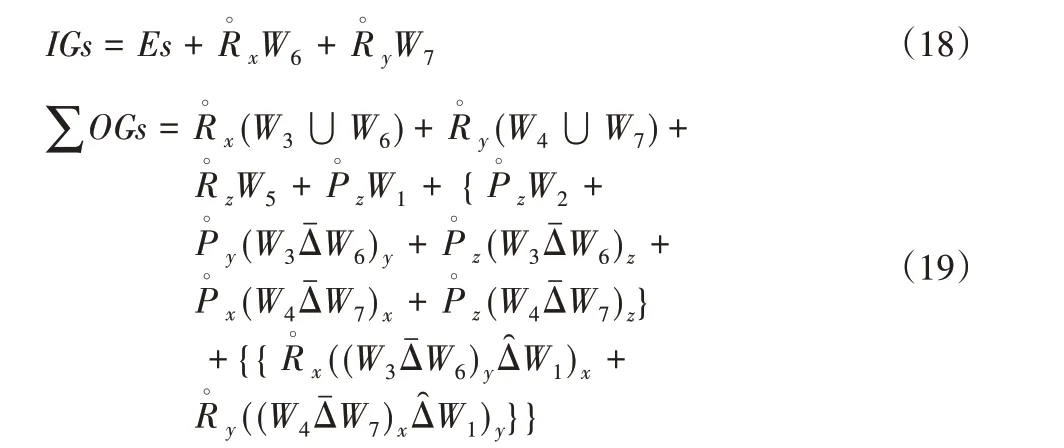
依据式（19）的计算分析结果，可以得知混联机构的M−DOF=4，P−DOF=5，O−DOF=6。

本例证明了以等效串联机构或关节代替分析并联机构的输出运动能力特性和以广义等效串联机构代替分析混联机构的输出运动能力特性的研究路线是正确的，基于“最短支链∕支链对”的并联机构输出运动能力特性“木桶原理分析法”能够在解决混联机构输出运动能力特性分析问题过程中发挥重要作用。

6 结论

提出了基于“最短支链∕支链对”的并联机构输出运动能力特性“木桶原理分析法”，同时基于主−副运动理论，运用机构输入−输出运动综合转化公式和解析分析，针对7种不同姿态下的SPS∕SPU∕UPS结构的4−6支链并联机构的输出运动特性进行了分类对比研究。并借助等效串联机构、广义等效串联机构的概念，对2SPS−3SPU−RR混联机构的输出运动特性进行了分析计算，得到如下结论：

（1）支链的空间姿态是水平面内一个或两个方向的主输出移动运动是否存在的决定因素。构建固定坐标系令某一个或两个支链分别位于其铅垂面上，可以使机构水平面内1个或2个输出主运动分量消失。最短支链的空间姿态是水平面内x/y方向的主输出移动运动分量是否存在的决定因素；最短支链对的空间姿态对于水平面内x、y方向主输出移动运动是否存在具有决定作用。

（2）动平台的空间姿态决定着水平面内一个方向的一阶伴随移动运动是否存在；动平台上关节位置、动平台结构和动平台空间姿态共同决定着水平面内2个方向的一阶伴随移动运动是否存在。最短支链∕支链对两端关节铰点到所在动、静平台形心的连线是否平行，决定了水平面内x∕y方向的一阶伴随移动运动是否存在。最短支链对两端关节铰点到所在动、静平台形心的连线在各自平台平面内是否正交，以及最短支链对两端关节铰点到所在动、静平台形心的连线是否均分别平行，决定了水平面内x、y方向的一阶伴随移动运动是否存在。

（3）构建固定坐标系使某一个或两个支链分别位于其铅垂面上，可令机构水平面内1个或2个输出主运动分量消失；而选择静平台平面与固定坐标系的水平面重合，能达到使机构水平面内1个或2个一阶伴随移动输出分量消失的效果。

（4）并联机构可以用等效串联机构或关节代替分析其输出运动能力特性，而混联机构可以用广义等效串联机构代替分析其运动能力特性。混联机构输出运动能力特性计算实例证明了基于“最短支链∕支链对”的并联机构输出运动能力特性“木桶原理分析法”在系统分析机构输出运动特性的有效性。