起重机系统运动轨迹逆动态控制研究
2022-12-30张家海
徐 智,张家海
(三江学院机械与电气工程学院,江苏 南京 210012)
1 引言
在汽车生产和钢铁冶炼过程中,通常需要进行钢材的运输。传统的起重机吊装方法,不仅效率低,而且危险性也较高。起重机在吊装负载过程中,随着起重机小车的加速或减速行驶,负载也会随之摆动[1−2]。依靠空气阻力使起重机负载摆动幅度降低往往需要浪费大量的时间,导致工作效率降低。除此之外,负载的摆动还会导致定位精度降低。随着起重机吊装负载的高度和速度增加,负载的摆动幅度也在增加,这也使得小车定位问题变得越来越突出。如果仍然采取传统的人工防止摆动来进行控制,将难以达到高精度定位目标。因此,无论是从起重机设备安全和效率角度考虑,还是从负载定位精度考虑,对于起重机控制系统的研究都具有十分重要的意义。
目前,对起重机负载控制系统的研究虽然很多,但是还是有许多不足之处,一些文献研究的控制器并没有考虑起重机模型的非线性、时变性等问题。例如:文献[3−4]研究了起重机负载的PID控制方法,通过拉普拉斯变换推导出起重机运动学方程式,引用了PID控制方法,搭建了起重机负载控制仿真模型,在不同摆角条件下对负载摇摆进行控制,在一定程度上提高了系统反应速度和抗干扰能力。文献[5−6]研究了起重机负载的模糊自适应PID控制系统,建立小车、货物系统的数学模型,通过拉格朗日方程推导出负载动态方程式,设计了模糊自适应PID 控制器,采用MAT⁃LAB软件对模糊自适应PID控制进行仿真,降低了负载的摆动角度和振动幅度。文献[7−8]研究了起重机负载神经网络PID控制方法,建立起重机简图模型,对小车进行了动力学分析,采用传统PID控制和单神经元相结合的方式,给出了起重机负载神经网络PID 控制流程,通过仿真验证起重机负载运动过程中的摆动幅度,从而提高了负载定位精度和系统的响应速度。以往研究的起重机控制系统响应速度较慢,导致控制精度较低。
对此,创建了起重机运动模型装置示意图,推导出起重机运动方程式,为了提高控制系统的抗干扰能力,采用人工神经网络与逆动态控制相结合方法,并给出起重机模型控制流程。为了进一步验证人工神经网络逆动态控制效果,采用MATLAB 软件对起重机负载运动输出效果进行仿真,并且与传统PID控制输出效果进行对比,为深入研究起重机控制系统的设计提供参考价值。
2 起重机系统建模
起重机模型,如图1所示。其运动方程为:
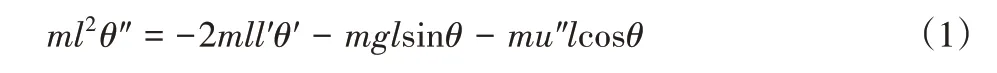
式中:x—负载位移;u"—小车加速度;l—长度;θ—角位移;θ′—角速度;θ″—角加速度;m—负载质量。
影响起重机响应的因素除了控制系统,还有机械结构,如图1所示。

图1 起重机模型简图Fig.1 Crane Model Diagram
式中:θ1—吊钩在位置1处与垂直方向的夹角;θ2—吊钩在位置2处与垂直方向的夹角;l1—吊钩在位置1处与机械滚筒之间的垂直距离;l2—吊钩在位置2处与机械滚筒之间的垂直距离;r1—机械滚筒的半径;r2—吊钩的半径。
3 控制器设计
3.1 PID控制
PID控制是当前较为流行的控制系统,主要由比例、积分和微分三个部分组成,如图2所示。
在图2中,r(t)表示控制系统的输入量;y(t)表示控制系统的输出量;e(t)表示输入与输出值之间的误差;u(t)为控制方程。

图2 PID控制系统Fig.2 PID Control System
大多数情况下,PID控制采用增量式控制形式,其控制方程式[9]如下所示:

式中:t—采样间隔时间;kp—比例调整系数;Ti—积分时间常数;Td—微分时间常数。
PID控制系统通过调整比例系数、积分常数和微分常数,从而使控制对象输出误差降低。
3.2 逆动态控制
起重机作为前驱动系统,其控制是一项复杂的任务。该模型可通过逆计算得到解析动力学模型。它需要根据系统的动力学精确地制定。解析模型可以用数值计算来近似。然而,这种模型并不总是保证控制性能。该控制器利用神经网络求解起重机的逆动态问题。人工神经网络算法具有学习非线性和其他不易建模的外部或内部因素的潜力。
逆动力学模型可以直接配置神经网络的参数,利用系统的动力学信息对其进行训练和验证,并在相应的逆模型中优化学习规律结构可以表示起重机的模型为:

将逆动力学模型的输出y(t+1)替换为输入参考r(t+1)作为控制器。
3.3 神经网络逆动态控制
神经网络的结构可以用输入、隐藏层、输出、神经元以及与权值和偏差信息的相互关联来表示。逆动态控制中的神经网络结构,如图3所示。

图3 起重机系统逆动态控制Fig.3 Inverse Dynamic Control of Crane System

神经网络逆动态控制的主要输入基准是小车速度v(t)的信号,输出是小车u(t)的控制信号。逆控制器的输入为:小车速度参考值r(t)、回归器结构的输入数量为[q−1,q−2,…,q−n]和输出数量为[q−1,q−2,…,q−m],其定义了模型配置中的回归向量结构,以及负载速度。

式中:p(t)—2n的周期信号。
随机二进制信号中的最大长度均值和协方差定义如下:

式中:M—频率峰值;随机二进制信号具有整周期。
4 结果与分析
为了验证人工神经网络逆动态控制效果,采用MATLAB 软件对起重机负载运动的位移、速度和加速度进行仿真,在不同环境中与传统PID控制输出效果进行对比,仿真参数,如表1所示。

表1 仿真参数Tab.1 Simulation Parameters
假设负载运动位移表达式为:

假设在无外界波形干扰条件下,则起重机负载运动位移跟踪误差,如图4所示。

图4 负载位移(无干扰)Fig.4 Load Displacement(No Interference)
起重机负载运动速度跟踪误差,如图5所示。起重机负载运动加速度跟踪误差,如图6所示。

图5 负载速度(无干扰)Fig.5 Load Speed(No Interference)

图6 负载加速度(无干扰)Fig.6 Load Acceleration(No Interference)
假设在小波形干扰条件下(x=10sin2πt),则起重机负载运动位移跟踪误差,如图7所示。

图7 负载位移(小干扰)Fig.7 Load Displacement(Small Interference)
起重机负载运动速度跟踪误差,如图8所示。起重机负载运动加速度跟踪误差,如图9所示。假设在大波形干扰条件下(x=100sin2πt),则起重机负载运动位移跟踪误差,如图10所示。

图8 负载速度(小干扰)Fig.8 Load Speed(Small Interference)

图9 负载加速度(小干扰)Fig.9 Load Acceleration(Small Interference)

图10 负载位移(大干扰)Fig.10 Load Displacement(Large Disturbance)
起重机负载运动速度跟踪误差,如图11所示。起重机负载运动加速度跟踪误差,如图12所示。

图11 负载速度(大干扰)Fig.11 Load Speed(Large Disturbance)

图12 负载加速度(大干扰)Fig.12 Load Acceleration(Large Disturbance)
由图4~图6可知,在无外界波形干扰条件下,采用PID控制和人工神经网络逆动态控制,起重机负载运动位移、速度和加速度跟踪误差较小,说明负载上下振动幅度较小,控制精度较高。由图7~图9可知,在小波形干扰条件下,采用PID控制,起重机负载运动位移、速度和加速度跟踪误差较大,说明负载上下振动幅度较大,控制精度较低;采用人工神经网络逆动态控制,起重机负载运动位移、速度和加速度跟踪误差较小,说明负载上下振动幅度较小,控制精度较高。由图10~图12可知,在大波形干扰条件下,采用PID控制,起重机负载运动位移、速度和加速度跟踪误差进一步增大,说明负载上下振动幅度进一步增大,控制精度进一步降低;采用人工神经网络逆动态控制,起重机负载运动位移、速度和加速度跟踪误差仍然较小,说明负载上下振动幅度较小,控制精度较高。因此,在相同条件下,采用PID控制方法,起重机负载运动跟踪误差较大,运动不平稳,而采用人工神经网络逆动态控制方法,起重机负载运动跟踪误差较小,振动幅度较小,运动相对平稳。
5 结语
针对起重机负载运动轨迹精度较低、振动幅度较大问题,设计人工神经网络逆动态控制系统,通过仿真验证起重机负载控制效果,主要结论如下:
(1)在无外界波形干扰环境中,采用传统PID控制和人工神经网络控制系统,起重机负载运动位移、速度和加速度跟踪误差较小,负载运动过程中抖动幅度较小,运动相对稳定。
(2)在有外界波形干扰环境中,采用PID控制方法,起重机负载运动位移、速度和加速度跟踪误差较大,负载运动不稳定,而采用人工神经网络控制系统,起重机负载运动位移、速度和加速度跟踪误差较小,负载运动更加稳定。
(3)随着外界干扰波形幅度的增大,起重机负载运动轨迹跟踪误差也随着增大,而采用MATLAB 软件对起重机负载控制系统进行仿真,通过不同工况条件下检验抗干扰能力,能够提高设计效率,避免设计不当而造成资源的浪费。
